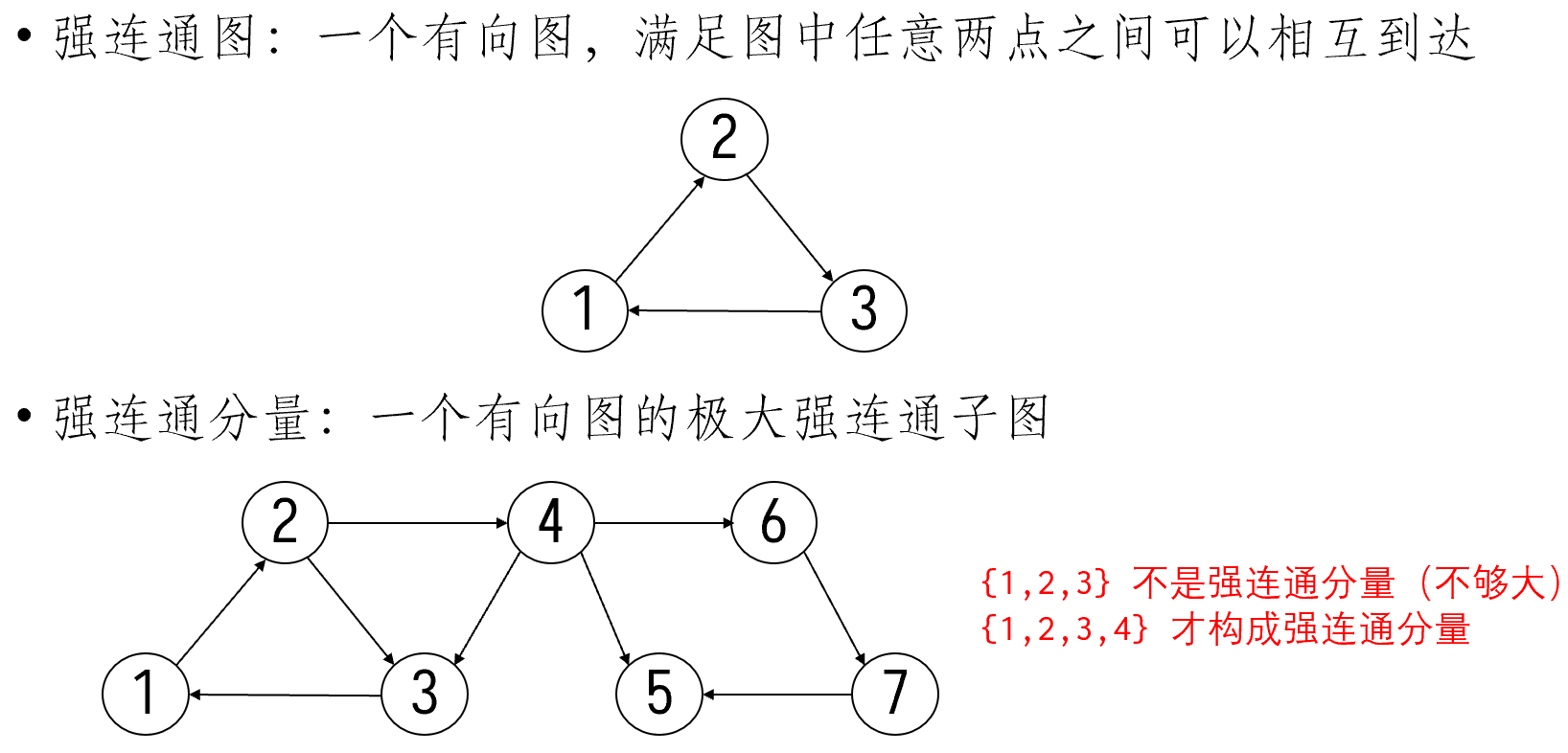
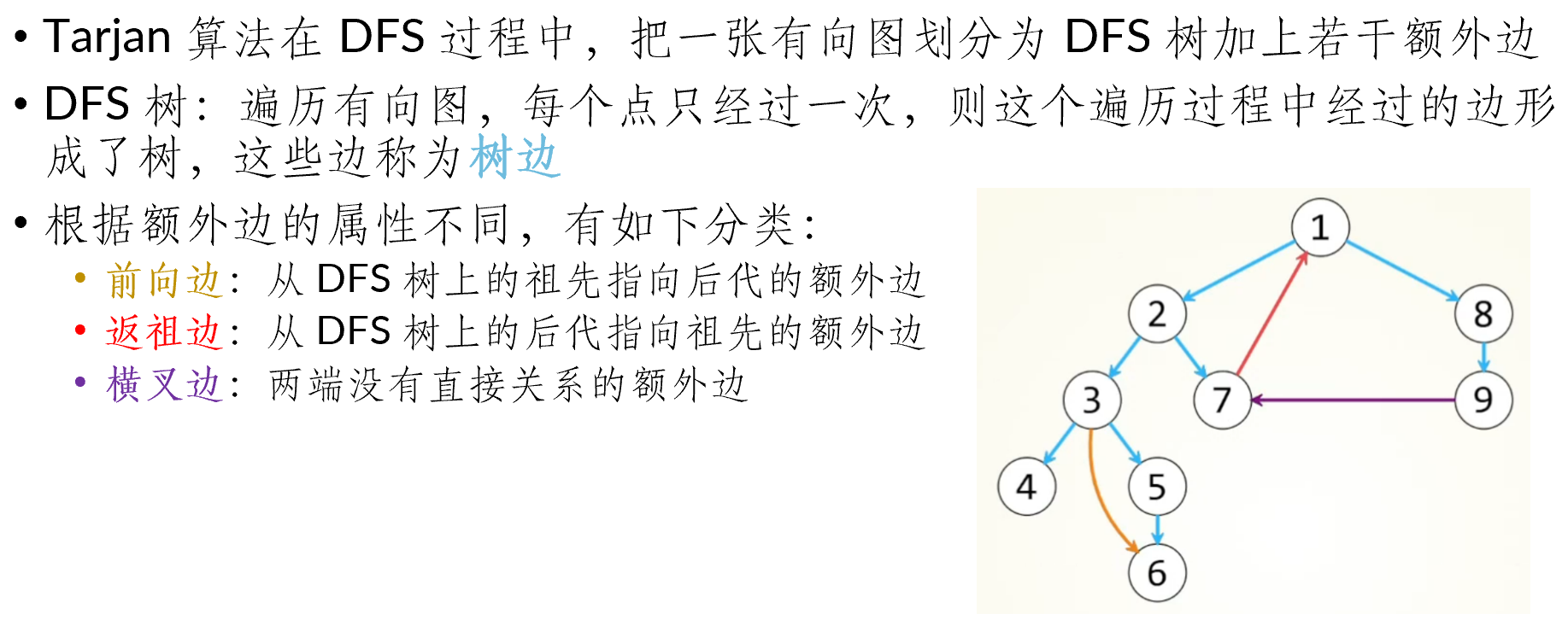
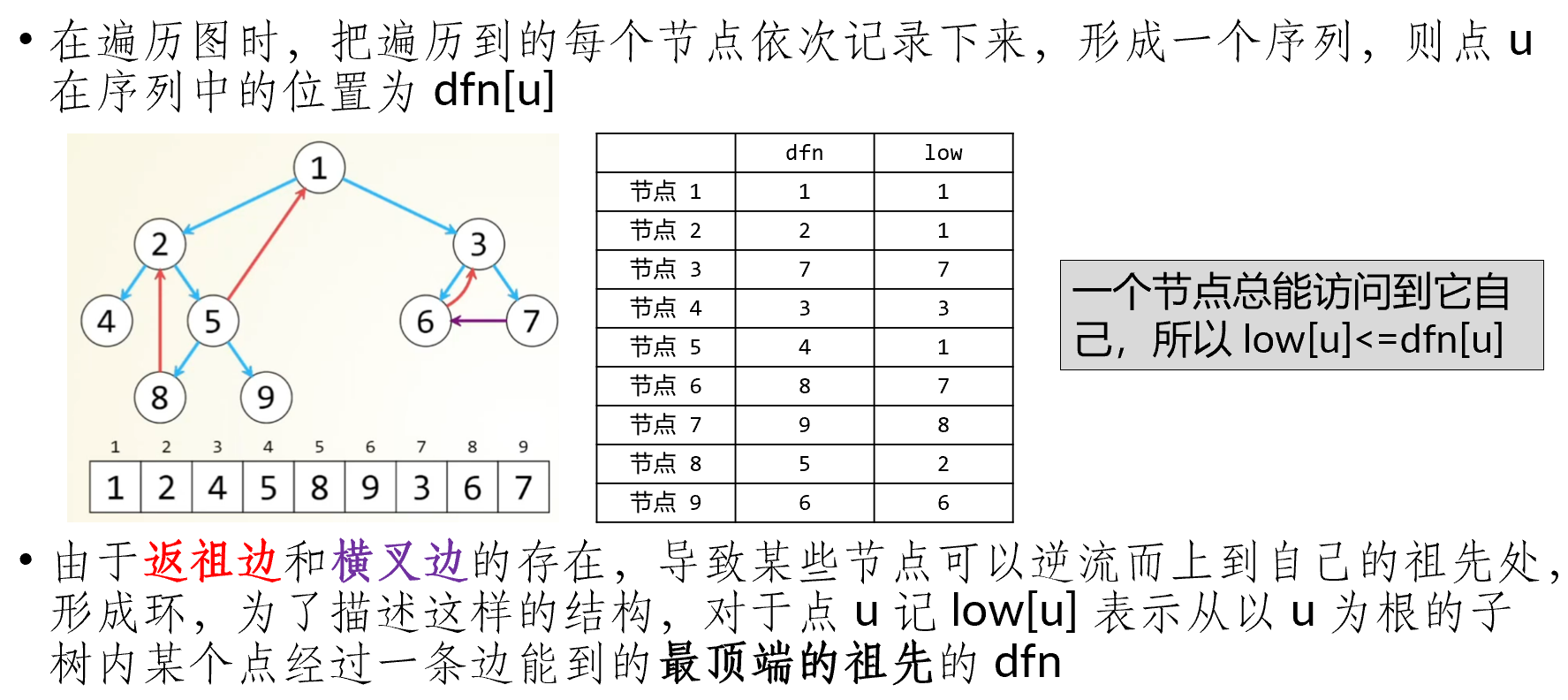
有向图的强连通分量




int dfn[N], low[N], scc[N], tot, cnt;
bool ins[N];
stack<int> s;
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
s.push(u); ins[u] = true;
for (int v : g[u]) {
if (!dfn[v]) { // 树边
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (ins[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
cnt++; // 新增一个强连通分量
while (s.top() != u) {
scc[s.top()] = cnt; // u属于第cnt个强连通分量
ins[s.top()] = false;
s.pop();
}
scc[u] = cnt; ins[u] = false; s.pop();
}
}
习题:P2863 [USACO06JAN] The Cow Prom S
解题思路
在求强连通分量时记录每个强连通分量大小,统计大于 \(1\) 的个数。
参考代码
#include <cstdio>
#include <vector>
#include <stack>
#include <algorithm>
using namespace std;
const int N = 10005;
int low[N], dfn[N], tot, cnt, scc[N], sz[N], ans;
vector<int> g[N];
bool ins[N];
stack<int> s;
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
s.push(u); ins[u] = true;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (ins[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
cnt++;
while (s.top() != u) {
scc[s.top()] = cnt;
sz[cnt]++;
ins[s.top()] = false;
s.pop();
}
scc[u] = cnt; ins[u] = false; s.pop(); sz[cnt]++;
if (sz[cnt] > 1) ans++;
}
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int a, b;
scanf("%d%d", &a, &b);
g[a].push_back(b);
}
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i);
printf("%d\n", ans);
return 0;
}
习题:P1407 [国家集训队] 稳定婚姻
解题思路
对于情侣关系,规定边的方向为女指向男,对于前任关系,规定边的方向为男指向女,这样建图如果某对情侣在同一个强连通分量中,说明这两人离婚后可以演化出其他婚姻关系(通过环),因此是 unsafe 的。
参考代码
#include <iostream>
#include <string>
#include <map>
#include <vector>
#include <stack>
#include <algorithm>
using std::cin;
using std::cout;
using std::min;
using std::string;
using std::map;
using std::vector;
using std::stack;
const int N = 8005;
map<string, int> id;
vector<int> g[N];
stack<int> s;
bool ins[N];
int dfn[N], low[N], tot, cnt, scc[N];
string name[N];
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
s.push(u); ins[u] = true;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (ins[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
cnt++;
while (true) {
int v = s.top(); s.pop(); ins[v] = false;
scc[v] = cnt;
if (v == u) break;
}
}
}
int main()
{
int n; cin >> n;
for (int i = 1; i <= n; i++) {
string girl, boy;
cin >> girl >> boy;
name[i] = girl; name[n + i] = boy;
id[girl] = i; id[boy] = n + i;
g[i].push_back(n + i);
}
int m; cin >> m;
for (int i = 1; i <= m; i++) {
string girl, boy;
cin >> girl >> boy;
g[id[boy]].push_back(id[girl]);
}
for (int i = 1; i <= n * 2; i++) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; i++)
cout << (scc[i] == scc[i + n] ? "Unsafe" : "Safe") << "\n";
return 0;
}
例题:P3387 【模板】缩点
如果图是一个 DAG,那么要计算最大的点权和路径就是一个经典的拓扑序 DP 问题。
而如果存在环,一旦选择了环上的某个点,则整个环上的点都可以走到,这样一定更优(允许多次经过同一个点或边,权值只计算一次)。因此可以把每个强连通分量中的点看成一个点(缩点),点权合并到同一个点上。
缩点之后重建的图必然是一个 DAG,在这个新的图上按拓扑序递推即可。
参考代码
#include <cstdio>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
using std::vector;
using std::stack;
using std::queue;
using std::min;
using std::max;
const int N = 10005;
int a[N], na[N], low[N], dfn[N], tot, scc[N], scc_cnt, ind[N], dp[N];
vector<int> g[N], ng[N];
bool ins[N];
stack<int> s;
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
s.push(u); ins[u] = true;
for (int v : g[u]) {
if (dfn[v] == 0) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (ins[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
scc_cnt++;
int v;
do {
v = s.top(); s.pop(); ins[v] = false;
scc[v] = scc_cnt; na[scc_cnt] += a[v];
} while (v != u);
}
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= m; i++) {
int u, v; scanf("%d%d", &u, &v);
g[u].push_back(v);
}
for (int i = 1; i <= n; i++) if (dfn[i] == 0) tarjan(i);
for (int u = 1; u <= n; u++) {
for (int v : g[u]) {
if (scc[u] != scc[v]) {
ng[scc[u]].push_back(scc[v]);
ind[scc[v]]++;
}
}
}
int ans = 0;
queue<int> q;
for (int i = 1; i <= scc_cnt; i++) if (ind[i] == 0) q.push(i);
while (!q.empty()) {
int u = q.front(); q.pop();
dp[u] += na[u]; ans = max(ans, dp[u]);
for (int v : ng[u]) {
dp[v] = max(dp[v], dp[u]);
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
printf("%d\n", ans);
return 0;
}
习题:P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G
解题思路
一个强连通分量中的任意两个点都互相“喜欢”,所以将原图提取强连通分量缩点重新建图之后,如果存在一个点能被其他所有点到达,则该点中的所有奶牛都是明星奶牛。这个点应当是新图上唯一的出度为 \(0\) 的点。
参考代码
#include <cstdio>
#include <vector>
#include <stack>
#include <algorithm>
using std::vector;
using std::stack;
using std::min;
const int N = 10005;
vector<int> g[N], ng[N];
int low[N], dfn[N], tot, scc[N], scc_cnt, sz[N], d[N];
stack<int> s;
bool ins[N];
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
s.push(u); ins[u] = true;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (ins[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
scc_cnt++;
int v;
do {
v = s.top(); s.pop(); ins[v] = false;
scc[v] = scc_cnt; sz[scc_cnt]++;
} while (v != u);
}
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int a, b; scanf("%d%d", &a, &b);
g[a].push_back(b);
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
for (int u = 1; u <= n; u++) {
for (int v : g[u]) {
if (scc[u] != scc[v]) {
ng[scc[u]].push_back(scc[v]);
d[scc[u]]++;
}
}
}
int ans = 0;
for (int i = 1; i <= scc_cnt; i++)
if (d[i] == 0) {
if (ans != 0) {
ans = 0; break;
}
ans = sz[i];
}
printf("%d\n", ans);
return 0;
}
习题:P2746 [USACO5.3] 校园网Network of Schools
解题思路
一个强连通分量中的学校都可以互相接收软件,考虑缩点。
子任务 A 相当于求缩点后的图中有多少个入度为 \(0\) 的点。
子任务 B 相当于求缩点后的图最少再加多少条边可以形成强连通分量。
如果缩点后只剩一个点则不需要添加额外的边,已经是一个强连通分量了。
如果缩点后不止一个节点,设缩点后的图中入度为 \(0\) 的点集为 \(S\),出度为 \(0\) 的点集为 \(T\)。新增的边只需要让 \(T\) 中的点连向 \(S\) 中的点,但是并不是任意连接的。具体的方案是:根据 \(S\) 中的点和 \(T\) 中的点的连通关系构建一个二分图,对这个二分图做最大匹配,则得到 \(k\) 组匹配关系,这里的 \(k\) 一定等于 \(\min \{ |S|, |T| \}\),记这些匹配的点对为 \(S_1, T_1, S_2, T_2, \dots\),让 \(T_1\) 向 \(S_2\) 连边,\(T_2\) 向 \(S_3\) 连边,……,\(T_k\) 向 \(S_1\) 连边,这样一来这 \(k\) 对点之间已经实现了互相连通。此时如果 \(S\) 中还有一些剩余的未匹配点,让 \(T\) 中任意一个点向这些 \(S\) 中未匹配的点连边;如果是 \(T\) 中还有一些剩余的未匹配点,让这些点都连向 \(S\) 中的某个点。总共需要增加的边数是 \(\max \{ |S|, |T| \}\)。
参考代码
#include <cstdio>
#include <vector>
#include <stack>
#include <algorithm>
using std::vector;
using std::stack;
using std::min;
using std::max;
const int N = 105;
vector<int> g[N];
stack<int> s;
int tot, low[N], dfn[N], scc[N], cnt, in[N], out[N];
bool ins[N];
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
s.push(u); ins[u] = true;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (ins[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
cnt++;
while (s.top() != u) {
scc[s.top()] = cnt;
ins[s.top()] = false;
s.pop();
}
scc[u] = cnt; ins[u] = false; s.pop();
}
}
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
int x;
while (scanf("%d", &x) && x != 0) g[i].push_back(x);
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; i++)
for (int j : g[i])
if (scc[i] != scc[j]) {
out[scc[i]]++; in[scc[j]]++;
}
int cnt1 = 0, cnt2 = 0;
for (int i = 1; i <= cnt; i++) {
if (in[i] == 0) cnt1++;
if (out[i] == 0) cnt2++;
}
printf("%d\n%d\n", cnt1, cnt == 1 ? 0 : max(cnt1, cnt2));
return 0;
}
习题:P2272 [ZJOI2007] 最大半连通子图
解题思路
一个强连通分量中的点可以两两互相到达,那就更加满足“半连通”的要求了,因此一个强连通分量里的点可以全选。
缩点重新建图后得到 DAG,在这个 DAG 中半连通子图必然是一条链。因此最大半连通子图的节点数 \(k\) 实际上就是最长链的长度(一个强连通分量缩成的点的“长度”为其内部节点数量),不同的最大半连通子图数目就是最长链的方案数。
注意在缩点建图时某两个强连通分量之间的连边可能会有多条,但是在考虑方案数时都是同一种情况,因此重新建图之前要先去掉重边。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
#include <stack>
#include <queue>
using std::vector;
using std::stack;
using std::queue;
using std::min;
using std::max;
using std::sort;
using std::unique;
const int N = 100005;
vector<int> g[N], ng[N];
int dfn[N], low[N], tot, cnt, scc[N], sz[N], ind[N], dp[N], c[N];
stack<int> s;
bool ins[N];
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
s.push(u); ins[u] = true;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (ins[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
cnt++;
while (true) {
int v = s.top(); s.pop(); ins[v] = false;
scc[v] = cnt; sz[cnt]++;
if (v == u) break;
}
}
}
int main()
{
int n, m, x; scanf("%d%d%d", &n, &m, &x);
for (int i = 1; i <= m; i++) {
int a, b; scanf("%d%d", &a, &b);
g[a].push_back(b);
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
for (int u = 1; u <= n; u++) {
for (int v : g[u]) {
int su = scc[u], sv = scc[v];
if (su != sv) {
ng[su].push_back(sv);
}
}
}
for (int i = 1; i <= n; i++) {
sort(ng[i].begin(), ng[i].end());
ng[i].erase(unique(ng[i].begin(), ng[i].end()), ng[i].end());
for (int j : ng[i]) ind[j]++;
}
queue<int> q;
for (int i = 1; i <= cnt; i++)
if (ind[i] == 0) {
q.push(i); dp[i] = sz[i]; c[i] = 1;
}
int ansk = 0;
while (!q.empty()) {
int u = q.front(); q.pop();
ansk = max(ansk, dp[u]);
for (int v : ng[u]) {
if (dp[u] + sz[v] > dp[v]) {
dp[v] = dp[u] + sz[v];
c[v] = c[u];
} else if (dp[u] + sz[v] == dp[v]) {
c[v] += c[u]; c[v] %= x;
}
ind[v]--;
if (ind[v] == 0) q.push(v);
}
}
int ansc = 0;
for (int i = 1; i <= cnt; i++)
if (dp[i] == ansk) ansc = (ansc + c[i]) % x;
printf("%d\n%d\n", ansk, ansc);
return 0;
}
习题:P2515 [HAOI2010] 软件安装
解题思路
软件之间的依赖关系可能构成环,所以需要先将强连通分量缩点,相当于循环依赖的软件要么都装要么都不装。缩点后得到有向的森林,可以加一个虚拟节点 \(0\) 连向所有入度为 \(0\) 的点,转化为一棵树,那么这就是一个经典的树上背包问题了。
参考代码
#include <cstdio>
#include <vector>
#include <stack>
#include <algorithm>
using std::vector;
using std::stack;
using std::min;
using std::max;
const int N = 105;
const int M = 505;
int n, m, w[N], nw[N], v[N], nv[N];
int dfn[N], low[N], tot, scc[N], cnt, ind[N], dp[N][M], sum[N];
vector<int> g[N], ng[N];
stack<int> s;
bool ins[N];
void tarjan(int u) {
dfn[u] = low[u] = ++tot;
s.push(u); ins[u] = true;
for (int v : g[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (ins[v]) {
low[u] = min(low[u], dfn[v]);
}
}
if (low[u] == dfn[u]) {
cnt++;
while (true) {
int x = s.top(); s.pop(); ins[x] = false;
scc[x] = cnt; nv[cnt] += v[x]; nw[cnt] += w[x];
if (x == u) break;
}
}
}
void dfs(int u) {
sum[u] = nw[u];
for (int i = m; i >= nw[u]; i--) dp[u][i] = nv[u];
for (int v : ng[u]) {
dfs(v);
for (int i = min(sum[u], m); i >= nw[u]; i--) {
for (int j = min(m - i, sum[v]); j >= 0; j--) {
dp[u][i + j] = max(dp[u][i + j], dp[u][i] + dp[v][j]);
}
}
sum[u] += sum[v];
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
for (int i = 1; i <= n; i++) scanf("%d", &v[i]);
for (int i = 1; i <= n; i++) {
int d; scanf("%d", &d);
g[d].push_back(i);
}
for (int i = 1; i <= n; i++) if (!dfn[i]) tarjan(i);
for (int u = 1; u <= n; u++) {
for (int v : g[u]) {
if (scc[u] != scc[v]) {
ng[scc[u]].push_back(scc[v]);
ind[scc[v]]++;
}
}
}
for (int i = 1; i <= cnt; i++) {
if (ind[i] == 0) ng[0].push_back(i);
}
dfs(0);
printf("%d\n", dp[0][m]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号