树状数组
树状数组(Binary Indexed Tree,BIT)是一种用于维护 \(n\) 个元素的前缀信息的数据结构。
以前缀和为例,对于数列 \(a\),可以将其存储为前缀和数组 \(s\) 的形式,其中 \(s_i = \sum \limits_{j=1}^i a_j\)。那么通过前缀和数组,就可以快速求出原数组中给定区间中数字的和:对于区间 \([l,r]\),区间和为 \(s_r - s_{l-1}\),其中假设 \(s_0 = 0\)。
显然,对于长度为 \(n\) 的数列,前缀和需要用长度为 \(n\) 的数组进行存储。而当数列 \(a\) 发生变化时,要使得 \(s\) 数组的内容仍能够正确对应数列 \(a\) 的前缀和,就需要对 \(s\) 的值进行修改,即使数列中只有一个数发生变化,也可能需要修改 \(s\) 数组的多个值,才能保证整个数组仍然存储的是 \(a\) 的前缀和。
类似地,对于长度为 \(n\) 的数列,树状数组也会使用长度为 \(n\) 的数组来进行存储。在这个数组中,每个位置存储的内容则稍微有些复杂。
例题:P3374 【模板】树状数组 1
已知一个数列,需要支持两种操作:
1. 将某一个数加上 \(x\);
2. 求出某区间中每一个数的和并输出。
数列长度和操作个数均不超过 \(5 \times 10^5\)。
分析:如果使用朴素的做法,将这个数列保存在一个数组 \(a\) 中,那么对于第二种操作,需要将查询区间内的每一个数依次加起来。如果这样做,那么最坏情况下每一次操作就要遍历整个数组,导致超时。
另一种想法是,通过将数列存储为前缀和数组 \(s\) 的形式,那么就可以快速求出给定区间的和;然而,对于第一种操作,在最坏情况下则又需要修改整个数组,同样会导致超时。
那么有没有方法可以结合两种做法的优势,使得两个操作均使用较低的时间复杂度来完成呢?这里就可以用到树状数组。
对于任何一种数据结构,可以将其抽象为一个黑匣子:黑匣子里面存储的是数据,可以向其提供支持的操作,包括修改操作和查询操作。当向其支持查询操作时,其需要通过保存的数据计算出需要的结果然后返回;当向其提供修改操作时,黑匣子需要更新其内部的数据,来保证对于之后的查询操作,黑匣子仍能够返回正确的结果。能否解决问题取决于这个黑匣子是否能以及能以何种复杂度实现这些操作;而如何实现这样一个黑匣子,则是我们的任务。
在这个问题中,黑匣子需要维护一个数列,需要支持的有单点修改操作和区间查询操作。
和前缀和类似,树状数组每个位置保存的也是原数组中某一段区间的和。为了准确说明每个位置分别保存的是哪一段区间,首先引入一个函数 lowbit(x),它的值是 \(x\) 的二进制表达式中最低位的 \(1\) 所对应的值。例如,\(6\) 的二进制表示为 \((110)_2\),最低位的 \(1\) 为第二个 \(1\),其对应的值为 \((10)_2=(2)_{10}\),故 \(lowbit(6)=2\);\(20\) 的二进制表示为 \((10100)_2\),最低位的 \(1\) 为第二个 \(1\),其对应的值为 \((100)_2=(4)_{10}\),故 \(lowbit(20)=4\)。
在常见的计算机中,有符号数采用补码表示,而在补码表示下,\(lowbit(x)\) 有一种简单的表达方法:lowbit(x)=x&(-x),其中 & 为按位与。由于 \(-x\) 的补码为 \(x\) 按位取反后再加 \(1\),考虑 \(x\) 和 \(-x\) 的二进制表示,\(x\) 末尾的若干 \(0\) 在取反后变成 \(1\),加上 \(1\) 后变成 \(0\);\(x\) 最低位的 \(1\) 在取反后变成 \(0\),得到进位后变成 \(1\);比该位更高的不会得到进位,维持取反的状态。因此,在按位与的过程中,只有那一位得到的结果为 \(1\),其余都为 \(0\)。
x 二进制表示:0101...1000...0
-x 的反码表示:1010...0111...1
-x 的补码表示:1010...1000...0
那么,假设树状数组使用数组 \(c\) 来进行存储,原来的 \(n\) 个数分别为 \(a_1\) 到 \(a_n\),则 \(c_i = \sum \limits_{j=i-lowbit(i)+1}^i a_j\)。换句话说,树状数组中每个位置保存的是其向前 \(lowbit\) 长度的区间和。
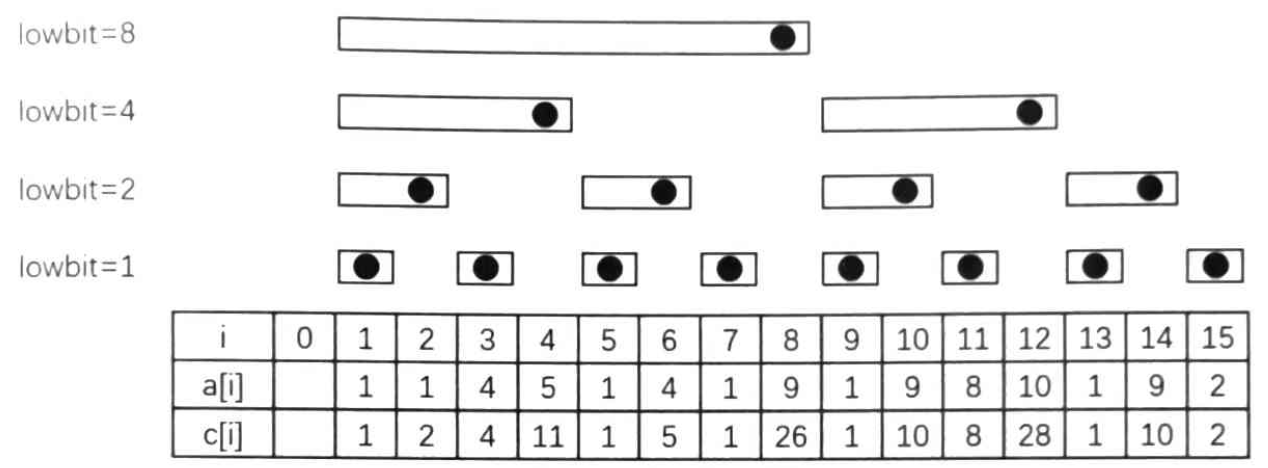
这样做有什么好处呢?考虑假设已经有了这样一个数组 \(c\),如何用它实现前缀和查询操作。假设要求 \(a_1\) 到 \(a_i\) 的前缀和 \(s_i\),可以先将 \(c_i\) 加入答案,那么剩下的部分就是 \(a_1\) 到 \(a_{i-lowbit(i)}\),换句话说,问题变成了求 \(s_{i-lowbit(i)}\)。那么接下来又可以将 \(c_{i-lowbit(i)}\) 加入答案,不断重复操作,直到问题变成求 \(s_0\) 为止,那么此时就已经得到 \(s_i\) 了。示例代码如下:
int query(int x) {
int res = 0;
while (x > 0) {
res += c[x]; x -= lowbit(x); // 从大到小将需要的值求和
}
return res;
}
这个过程的每一步中,把一个数 \(x\) 变成 \(x-lowbit(x)\),结合之前说的 \(lowbit\) 的含义,可以发现实际上是在不断地去掉 \(i\) 的二进制表示中最低位的 \(1\)。由于一个数 \(i\) 的二进制表示的位数不超过 \(\log i\),故每一次查询的时间复杂度为 \(O(\log n)\)。
接下来再考虑单点修改操作。假设修改的数是 \(a_i\),由于可能有多个位置对应的区间包含 \(a_i\),对于这些位置都要进行修改。
例如,要查询 \(s_{14}\) 的值,可以发现 \(s_{14}=c_{14}+c_{12}+c_8=64\);如果要修改 \(a_3\) 的值,则需修改所有包含 \(a_3\) 的区间值,也就是 \(a_3,a_4\) 和 \(a_8\)。
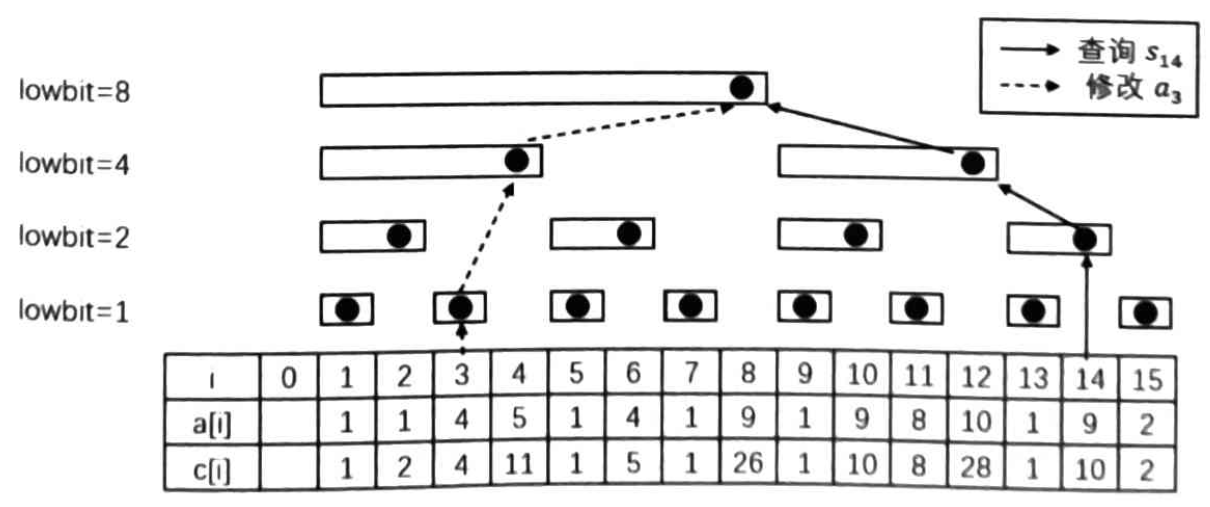
有哪些位置需要包含 \(a_i\) 呢?先考虑几个结论,假设一个位置 \(c_j\) 包含 \(a_i\),那么有:
- \(j \ge i\)。这一点很显然,因为一个位置只会包含它前面的数。
- \(lowbit(j) \ge lowbit(i)\),当且仅当 \(j=i\) 时取等号。
- \(lowbit\) 的值相等的位置不会包含同一个数。
综合以上的结论,可以按 \(lowbit\) 从小到大的顺序找出满足条件的 \(j\)。
首先,\(i\) 是第一个满足条件的 \(j\),记为 \(j_0=i\)。
下一个 \(j\) 需要比 \(i\) 大,且 \(lowbit\) 也要更大,即二进制表示中末尾的 \(0\) 更多,因此至少需要把最后一个 \(1\) 变成 \(0\),也就是至少加上 \(lowbit(j_0)\);由于 \(lowbit(j_0)<lowbit(j_0+lowbit(j_0))\),而 \(j_0=i\),所以 \(i\) 显然在 \(j_0+lowbit(j_0)\) 对应的区间内,也就是说 \(j_0+lowbit(j_0)\) 就是下一个 \(j\),记为 \(j_1=j_0+lowbit(j_0)\)。
再下一个 \(j\) 又可以通过 \(j_1+lowbit(j_1)\) 得到,由于 \(lowbit\) 是翻倍增长的,所以 \(lowbit(j_0)+lowbit(j_1)\) 仍然小于 \(lowbit(j_1)+lowbit(j_1)\),意味着 \(i\) 也在 \(j_1+lowbit(j_1)\) 所对应的区间内,即 \(j_2=j_1+lowbit(j_1)\)。以此类推,即可得到所有需要修改的位置。示例代码如下:
void add(int x, int y) {
while (x <= n) {
c[x] += y; x += lowbit(x); // 从小到大修改需要修改的位置
}
}
由于 \(lowbit\) 的值只有不超过 \(\log n\) 种,一次修改中一个 \(lowbit\) 值最多只会对应一个需要的位置,所以每一次修改的时间复杂度也为 \(O(\log n)\)。
至此,我们知道树状数组可以维护一个数列,并以 \(O(\log n)\) 的时间复杂度进行单点修改操作和前缀和查询操作。对于本题,要实现的是区间和查询操作,可以通过前缀和查询操作来实现:对于 \([l,r]\) 的查询,只需要用 \([1,r]\) 的和减去 \([1,l-1]\) 的和即可。
#include <cstdio>
typedef long long LL;
const int MAXN = 5e5 + 5;
LL a[MAXN];
int n, m;
int lowbit(int x) {
return x & -x;
}
LL query(int x) {
LL ret = 0;
while (x > 0) {
ret += a[x];
x -= lowbit(x);
}
return ret;
}
void update(int x, LL d) {
while (x <= n) {
a[x] += d;
x += lowbit(x);
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
update(i, x);
}
while (m--) {
int op, x, y;
scanf("%d%d%d", &op, &x, &y);
if (op == 1) update(x, y);
else printf("%lld\n", query(y) - query(x - 1));
}
return 0;
}
例题:P3368 【模板】树状数组 2
已知一个数列,需要进行两种操作:将区间 \([x,y]\) 每一个数加上 \(x\);或者求出某一个数的值。
数列长度和操作个数均不超过 \(5 \times 10^5\)。
分析:和上个问题相反,这里需要对于数列实现区间加法的修改操作和单点的查询操作。乍一看好像没法使用树状数组,但实际上只需要进行一些小处理,就能把这个问题变得和上个问题相同。
对数组进行差分操作:假设原来的数列为 \(a\),令 \(b_i=a_i-a_{i-1}\),那么 \(a_i=\sum \limits_{j=1}^i b_j\),即 \(a\) 是 \(b\) 的前缀和数组。当 \(b_i\) 增加 \(x\) 时,意味着 \(a_i\) 到 \(a_n\) 都会增加 \(x\)。那么,对于 \(b\) 数组而言,第一个操作的效果为:假设要将区间 \([l,r]\) 的数增加 \(x\),则 \(b_l\) 增加 \(x\),\(b_{r+1}\) 减少 \(x\);第二个操作的效果为:求出 \(b\) 的某个前缀和。这样一来,\(b\) 数组就可以用树状数组进行维护。
#include <cstdio>
const int MAXN = 5e5 + 5;
int a[MAXN], n;
int lowbit(int x) {
return x & -x;
}
int query(int x) {
int ret = 0;
while (x > 0) {
ret += a[x];
x -= lowbit(x);
}
return ret;
}
void update(int x, int d) {
while (x <= n) {
a[x] += d;
x += lowbit(x);
}
}
int main()
{
int m, pre = 0;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
int x;
scanf("%d", &x);
update(i, x - pre);
pre = x;
}
while (m--) {
int op;
scanf("%d", &op);
if (op == 1) {
int x, y, k;
scanf("%d%d%d", &x, &y, &k);
update(x, k); update(y + 1, -k);
} else {
int x;
scanf("%d", &x);
printf("%d\n", query(x));
}
}
return 0;
}
例题:P1908 逆序对
对于给定的一段正整数序列,逆序对就是序列中 \(a_i>a_j\) 且 \(i<j\) 的有序对。给定长度为 \(n\) 的正整数序列,求逆序对数。其中 \(n \le 5 \times 10^5\)。
分析:考虑朴素的做法,枚举 \(i\),再枚举比 \(i\) 大的位置 \(j\),统计 \(a_j<a_i\) 的数量。假设把所有 \(j>i\) 中 \(a_j=k\) 的数量记为 \(cnt_k\),那么也就是统计 \(s_{a_i-1}=\sum \limits_{k=1}^{a_i-1} cnt_k\)。也就是说,查询的是一个数列 \(cnt\) 的前缀和。如果按照从大到小的位置枚举 \(i\),那么每当 \(i\) 前进一步,可用的 \(j\) 就增加一个,需要将 \(cnt_{a_j}\) 增加 \(1\)。可以发现,这是不断地在对数列 \(cnt\) 进行前缀和查询和单点修改操作,因此可以用树状数组维护数列 \(cnt\)。
但是还有一个问题:数列 \(cnt\) 的长度是多少呢?由于 \(a\) 中的元素可以很大,所以 \(cnt\) 的下标也可以很大。为了解决这个问题,可以用到离散化的思想。由于 \(cnt\) 数组开始时全为 \(0\),总共会进行 \(n\) 次修改,也就是说最多只有 \(n\) 个位置不是 \(0\)。因此可以只记录这些可能非 \(0\) 的位置。具体而言,首先将序列排序并去重,在这个序列上利用 std::lower_bound(),可以快速求出原数列中一个数是数列中的第几小。那么 \(cnt_k\) 可以表示序列中第 \(k\) 小的数的个数。这样一来,\(cnt\) 的长度就最多是 \(n\) 了。
#include <cstdio>
#include <vector>
#include <algorithm>
using std::lower_bound;
using std::sort;
using std::unique;
using std::vector;
typedef long long LL;
const int N = 5e5 + 5;
int n, a[N], bit[N], bound;
vector<int> data;
int discretization(int x) { // 求出x是第几小
return lower_bound(data.begin(), data.end(), x) - data.begin() + 1;
}
int lowbit(int x) {
return x & -x;
}
void add(int x) {
while (x <= bound) {
bit[x]++; x += lowbit(x);
}
}
int query(int x) {
int res = 0;
while (x > 0) {
res += bit[x]; x -= lowbit(x);
}
return res;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]); data.push_back(a[i]);
}
// 离散化的准备工作
sort(data.begin(), data.end());
data.erase(unique(data.begin(), data.end()), data.end());
bound = data.size();
LL ans = 0;
for (int i = n; i >= 1; i--) {
ans += query(discretization(a[i]) - 1);
add(discretization(a[i]));
}
printf("%lld\n", ans);
}
习题:P1637 三元上升子序列
解题思路
使用三层循环直接枚举所有满足 \(i \lt j \lt k\) 的三元组,然后判断值是否递增,对于 \(N = 3 \times 10^4\) 的数据规模,此方法会严重超时。
可以固定中间的元素 \(a_j\),然后分别统计:
- 在 \(j\) 左侧且值小于 \(a_j\) 的元素数量,记为 \(l\)。
- 在 \(j\) 右侧且值大于 \(a_j\) 的元素数量,记为 \(g\)。
对于固定的 \(j\),它能构成的三元上升子序列数量就是 \(l \times g\),将所有 \(j\) 的结果累加即可。这个算法的时间复杂度为 \(O(N^2)\)。
\(O(N^2)\) 算法的瓶颈在于为每个 \(j\) 计算 \(l\) 和 \(g\) 都需要 \(O(N)\) 的时间,可以使用树状数组这一数据结构来将这个计算过程优化到 \(O(\log N)\)。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 30005;
int n;
int a[N]; // 存储离散化后的排名
int discrete[N]; // 用于离散化的辅助数组
int less_counts[N]; // less_counts[i] 表示在 i 左侧且值比 a[i] 小的元素数量
int greater_counts[N]; // greater_counts[i] 表示在 i 右侧且值比 a[i] 大的元素数量
struct BIT {
int c[N], bound;
void clear() {
for (int i = 0; i <= bound; i++) c[i] = 0;
}
int lowbit(int x) {
return x & -x;
}
void update(int x, int d) {
while (x <= bound) {
c[x] += d;
x += lowbit(x);
}
}
int query(int x) {
int sum = 0;
while (x > 0) {
sum += c[x];
x -= lowbit(x);
}
return sum;
}
};
BIT cnt;
int main() {
scanf("%d", &n);
for (int i = 0; i < n; ++i) {
scanf("%d", &a[i]);
discrete[i] = a[i];
}
// --- 1. 离散化 ---
sort(discrete, discrete + n);
// m 是不重复元素的数量
int m = unique(discrete, discrete + n) - discrete;
// 将原数组 a 中的值替换为其在排好序的、不重复的数组中的排名(1-based)
for (int i = 0; i < n; ++i) {
a[i] = lower_bound(discrete, discrete + m, a[i]) - discrete + 1;
}
cnt.bound = m;
// --- 2. 计算 less_counts ---
cnt.clear();
for (int i = 0; i < n; ++i) {
// 查询已处理元素中,排名小于 a[i] 的元素数量
less_counts[i] = cnt.query(a[i] - 1);
// 将当前元素的排名信息更新到树状数组
cnt.update(a[i], 1);
}
// --- 3. 计算 greater_counts ---
cnt.clear();
for (int i = n - 1; i >= 0; --i) {
// 查询已处理元素(i右侧)中,排名大于 a[i] 的元素数量
// query(m) 是已处理元素总数,query(a[i]) 是排名 <= a[i] 的数量
greater_counts[i] = cnt.query(m) - cnt.query(a[i]);
// 将当前元素的排名信息更新到树状数组
cnt.update(a[i], 1);
}
// --- 4. 计算最终答案 ---
ll total_thairs = 0;
for (int i = 0; i < n; ++i) {
// 对于每个 a[i] 作为中间元素,其贡献为左右两侧满足条件的元素数量之积
total_thairs += 1ll * less_counts[i] * greater_counts[i];
}
printf("%lld\n", total_thairs);
return 0;
}
习题:P10589 楼兰图腾
解题思路
固定中间元素,对于序列中的每一个元素 \(y_j\),分别统计:
- 在它左侧比它大的元素数量 \(l_{\gt}\) 和比它小的元素数量 \(l_{\lt}\)。
- 在它右侧比它大的元素数量 \(r_{\gt}\) 和比它小的元素数量 \(r_{\lt}\)。
对于固定的 \(j\),它能作为中心构成的图腾数量为:
- \(\vee\) 图腾数:\(l_{\gt} \times r_{\gt}\)(因为 \(y_j\) 是谷底)
- \(\wedge\) 图腾数:\(l_{\lt} \times r_{\lt}\)(因为 \(y_j\) 是峰顶)
将所有 \(j\) 的贡献累加起来,就是最终的答案。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using std::vector;
using std::sort;
using std::lower_bound;
using std::unique;
using ll = long long;
const int N = 200005;
// y: 存储原始值,后转为离散化后的排名
ll y[N];
// data: 用于离散化的辅助vector
vector<ll> data;
// l1[i]: i左侧比y[i]大的元素数 (left_greater)
// r1[i]: i右侧比y[i]大的元素数 (right_greater)
// l2[i]: i左侧比y[i]小的元素数 (left_less)
// r2[i]: i右侧比y[i]小的元素数 (right_less)
// c: 树状数组本体
int n, l1[N], r1[N], l2[N], r2[N], c[N];
// 将原始值 x 映射为其在所有不重复值中的排名(1-based)
int discrete(ll x) {
return lower_bound(data.begin(), data.end(), x) - data.begin() + 1;
}
// --- 树状数组模板 ---
int lowbit(int x) {
return x & -x;
}
// 查询前缀和 [1, x]
int query(int x) {
int res = 0;
while (x > 0) {
res += c[x];
x -= lowbit(x);
}
return res;
}
// 在位置 x 增加 1
void update(int x) {
while (x <= n) {
c[x]++;
x += lowbit(x);
}
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%lld", &y[i]);
data.push_back(y[i]);
}
// --- 1. 离散化 ---
sort(data.begin(), data.end());
data.erase(unique(data.begin(), data.end()), data.end());
for (int i = 1; i <= n; i++) y[i] = discrete(y[i]);
// --- 2. 第一遍扫描 (从左到右),计算 l1 和 l2 ---
for (int i = 1; i <= n; i++) {
// query(n): 已处理元素总数 (i-1)
// query(y[i]): 已处理元素中排名 <= y[i] 的数量
// 两者之差即为排名 > y[i] 的数量
l1[i] = query(n) - query(y[i]);
// query(y[i] - 1): 已处理元素中排名 < y[i] 的数量
l2[i] = query(y[i] - 1);
// 将当前元素加入树状数组
update(y[i]);
}
// 清空树状数组以备第二遍扫描使用
for (int i = 1; i <= n; i++) c[i] = 0;
ll ans1 = 0, ans2 = 0; // ans1 存'V'图腾数, ans2 存'^'图腾数
// --- 3. 第二遍扫描 (从右到左),计算 r1, r2 并累加答案 ---
for (int i = n; i >= 1; i--) {
// 此时树状数组中包含的是 i 右侧的元素信息
// 计算右侧比 y[i] 大的元素数量
r1[i] = (n - i) - query(y[i]);
// V图腾: 左大 * 右大。累加到ans1
ans1 += 1ll * l1[i] * r1[i];
// 计算右侧比 y[i] 小的元素数量
r2[i] = query(y[i] - 1);
// ^图腾: 左小 * 右小。累加到ans2
ans2 += 1ll * l2[i] * r2[i];
// 将当前元素加入树状数组
update(y[i]);
}
// 按题目要求输出 'V' 的数量和 '∧' 的数量
printf("%lld %lld\n", ans1, ans2);
return 0;
}
习题:P5459 [BJOI2016] 回转寿司
给定一个长度为 \(n\) 的序列 \(a\),从中选出一段连续子序列 \([l,r]\),使得 \(L \le \sum \limits_{i=l}^r a_i \le R\),求方案数。
数据范围:\(1 \le n \le 10^5, |a_i| \le 10^5, 1 \le L,R \le 10^9\)。
解题思路
枚举 \(r = 1 \sim x\),求出对于每个 \(r\) 有多少 \(l\) 符合条件,累加即为答案。
先预处理出前缀和数组 \(sum\),那么 \(\sum \limits_{i=l}^r a_i\) 的值为 \(sum_r - sum_{l-1}\),当且仅当 \(L \le sum_r - sum_{l-1} \le R\) 时 \(l\) 符合条件。将式子变形,可得 \(sum_r - R \le sum_{l-1} \le sum_r - L\)。
所以只需要找到在 \(r\) 前面有多少个 \(sum_{l-1}\) 在 \([sum_r-R,sum_r-L]\) 这个值域范围内。这个问题可以对数据离散化后用树状数组维护,时间复杂度为 \(O(n \log n)\)。
参考代码
#include <cstdio>
#include <algorithm>
#include <vector>
typedef long long LL;
using std::sort;
using std::lower_bound;
using std::unique;
using std::vector;
const int N = 1e5 + 5;
int a[N], bit[N * 3], bound;
LL sum[N];
vector<LL> data;
int discretization(LL x) {
return lower_bound(data.begin(), data.end(), x) - data.begin() + 1;
}
int lowbit(int x) {
return x & -x;
}
void add(int x) {
while (x <= bound) {
bit[x]++;
x += lowbit(x);
}
}
int query(int x) {
int res = 0;
while (x > 0) {
res += bit[x];
x -= lowbit(x);
}
return res;
}
int main()
{
int n, l, r; scanf("%d%d%d", &n, &l, &r);
data.push_back(0);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]); sum[i] = sum[i - 1] + a[i]; // 预处理前缀和
data.push_back(sum[i]);
data.push_back(sum[i] - l);
data.push_back(sum[i] - r);
}
sort(data.begin(), data.end());
data.erase(unique(data.begin(), data.end()), data.end());
bound = data.size();
LL ans = 0;
add(discretization(0)); // sum[0]计数加1
for (int i = 1; i <= n; i++) { // 枚举右端点
int q1 = query(discretization(sum[i] - l));
int q2 = query(discretization(sum[i] - r) - 1);
ans += q1 - q2; // 累加在值域范围内的方案数
add(discretization(sum[i])); // sum[i]计数加1
}
printf("%lld\n", ans);
return 0;
}
习题:P5094 [USACO04OPEN] MooFest G 加强版
解题思路
暴力解法是枚举所有奶牛对,时间复杂度为 \(O(N^2)\)。对于 \(N=5 \times 10^4\) 的数据规模,该算法会超时。
公式中的 \(\max\) 和绝对值是处理的难点,因为它们的值取决于具体的 \(i\) 和 \(j\)。为了去掉这些动态变化的函数,一个常见的思路是排序。
可以尝试按坐标 \(x\) 排序或按听力 \(v\) 排序。
- 如果按 \(x\) 排序,可以去掉绝对值,但 \(\max (v_i, v_j)\) 依然难以处理。
- 如果按 \(v\) 排序,则可以方便地处理 \(\max\) 函数。
讲所有奶牛按照听力 \(v\) 从小到大进行排序,遍历排序后的奶牛数组。当处理到第 \(j\) 头牛时,计算它与所有在它之前处理过的奶牛(即 \(i \lt j\))的音量之和。
由于数组是按 \(v\) 排序的,对于任何 \(i \lt j\),都有 \(v_i \le v_j\)。因此,\(\max(v_i, v_j) = v_j\)。此时,第 \(j\) 头奶牛与前面所有奶牛的音量总和可以表示为:
通过这种方式,将 \(\max\) 从求和符号中提取出来。
现在,问题转化为:在遍历过程中,如何快速计算当前奶牛 \(j\) 与所有已处理奶牛 \(i\) 的坐标距离之和 \(\sum \limits_{i \lt j} |x_i - x_j|\)。
这个和式可以按 \(x_i\) 和 \(x_j\) 的大小关系拆为两部分:
- 对于坐标小于等于 \(x_j\) 的已处理奶牛,距离和为 \(\sum \limits_{i \lt j, \ x_i \le x_j} (x_j - x_i)\)。
- 对于坐标大于 \(x_j\) 的已处理奶牛,距离和为 \(\sum \limits_{i \lt j, \ x_i \gt x_j} (x_i - x_j)\)。
将这两部分展开,得到 \((\text{count}_{\le} \times x_j - \text{sum}_{\le}) + (\text{sum}_{\gt} - \text{count}_{\gt} \times x_j)\),其中:
- \(\text{count}_{\le}\) 表示已处理奶牛中,坐标 \(\le x_j\) 的数量。
- \(\text{sum}_{\le}\) 表示已处理奶牛中,坐标 \(\le x_j\) 的坐标之和。
- \(\text{count}_{\gt}\) 表示已处理奶牛中,坐标 \(\gt x_j\) 的数量。
- \(\text{sum}_{\gt}\) 表示已处理奶牛中,坐标 \(\gt x_j\) 的坐标之和。
为了在遍历过程中动态维护已处理奶牛的坐标信息,并快速查询上述四个值,树状数组是一个理想的数据结构。这里需要两个树状数组:一个维护每个坐标点上已出现的奶牛数量,另一个维护每个坐标点上奶牛的坐标之和。
排序的时间复杂度为 \(O(N \log N)\),遍历 \(N\) 头奶牛,每次遍历中涉及树状数组的查询和更新操作,单次操作复杂度为 \(O(\log \max \{ x \})\),这部分总复杂度为 \(O(N \log \max \{ x \})\)。由于 \(\max\{x\}\) 与 \(N\) 在同一数量级,总时间复杂度可视为 \(O(N \log N)\)。
参考代码
#include <cstdio>
#include <utility>
#include <algorithm>
using namespace std;
using ll = long long;
using pi = pair<int, int>;
const int N = 5e4 + 5;
// 使用 pair 存储奶牛信息,{v, x}
pi cow[N];
// 树状数组结构体
struct BIT {
int bound; // 树状数组的上界,即坐标最大值
ll c[N]; // 树状数组本体
// 计算 lowbit
int lowbit(int x) {
return x & -x;
}
// 查询前缀和,即查询坐标在 [1, x] 范围内的信息
ll query(int x) {
ll res = 0;
while (x > 0) {
res += c[x];
x -= lowbit(x);
}
return res;
}
// 在 x 位置上增加 d
void update(int x, int d) {
while (x <= bound) {
c[x] += d;
x += lowbit(x);
}
}
};
// 定义两个树状数组:
// tr_cnt: 用于维护坐标点上的奶牛数量
// tr_sum: 用于维护坐标点上奶牛的坐标之和
BIT tr_cnt, tr_sum;
int main()
{
int n;
scanf("%d", &n);
int x_max = 0;
for (int i = 1; i <= n; i++) {
int v, x; scanf("%d%d", &v, &x);
cow[i] = {v, x};
if (x > x_max) x_max = x; // 记录最大的坐标值
}
// 设置树状数组的边界
tr_cnt.bound = tr_sum.bound = x_max;
// 按奶牛的听力 v 对数组进行升序排序
// pair 默认按 first 元素排序,符合要求
sort(cow + 1, cow + n + 1);
ll ans = 0; // 存储最终答案
// 遍历排序后的奶牛数组
for (int i = 1; i <= n; i++) {
int v = cow[i].first, x = cow[i].second;
// --- 计算坐标 <= x 的已处理奶牛的音量贡献 ---
// 获取已处理奶牛中,坐标 <= x 的数量和坐标和
int cnt_le = tr_cnt.query(x);
ll sum_le = tr_sum.query(x);
// 距离和为 (cnt_le * x - sum_le),乘以 v 即为音量贡献
ans += (1ll * cnt_le * x - sum_le) * v;
// --- 计算坐标 > x 的已处理奶牛的音量贡献 ---
// 通过总量减去 <= x 的部分,得到 > x 的部分
int cnt_gt = tr_cnt.query(x_max) - cnt_le;
ll sum_gt = tr_sum.query(x_max) - sum_le;
// 距离和为 (sum_gt - cnt_gt * x),乘以 v 即为音量贡献
ans += (sum_gt - 1ll * cnt_gt * x) * v;
// --- 更新树状数组 ---
// 将当前奶牛的信息加入树状数组,以供后续奶牛计算
tr_cnt.update(x, 1);
tr_sum.update(x, x);
}
printf("%lld\n", ans);
return 0;
}
习题:P6186 [NOI Online #1 提高组] 冒泡排序
给定一个长度为 \(n\) 的排列 \(p\),\(m\) 个操作,需要支持两种操作:交换 \(p_x\) 和 \(p_{x+1}\);查询数组经过 \(k\) 轮冒泡排序后的逆序对个数。
数据范围:\(n,m \le 2 \times 10^5; 1 \le p_i \le n\)。
解题思路
设 \(f_i\) 表示在数字 \(i\) 左侧的比其大的数的个数,那么逆序对个数就是 \(\sum \limits_{i=1}^n f_i\)。
每经过一轮冒泡排序,若原本 \(f_i>0\),则一轮过后 \(f_i\) 会减一,否则保持不变,即等于 \(0\)。想象一下一轮冒泡排序的过程:如果 \(i\) 左边没有更大的数,则这个数左边的数不会跟它发生交换,则 \(f_i\) 仍等于 \(0\);如果左边有更大的数,则一轮冒泡过程中那个更大的数会和 \(i\) 发生交换从而使得 \(f_i\) 减一,并且在这一轮后面的过程中 \(i\) 的位置就不变了。
由上可知,经过 \(k\) 轮冒泡排序之后对逆序对还有贡献的是原本 \(f_i>k\) 的数。则答案为 \((\sum \limits_{f_i>k} f_i) - cnt \times k\),其中 \(cnt\) 代表满足 \(f_i>k\) 的 \(i\) 的个数。这正好是两种不同的前缀和(\(f_i\) 的前缀和以及 \(f_i\) 的个数的前缀和),可以通过树状数组维护。
针对交换操作,如果左小右大,则左边那个数对应的 \(f\) 在交换后会加一,如果左大右小,则右边那个数对应的 \(f\) 在交换后会减一,将其转化为相应树状数组上的更新操作即可。
参考代码
#include <cstdio>
#include <algorithm>
using std::swap;
using std::min;
typedef long long LL;
const int N = 2e5 + 5;
int n, p[N], f[N];
// 树状数组inv用于求一开始的f[i]
// 树状数组cnt用于维护f[i]的个数的前缀和
// 树状数组sum用于维护f[i]的前缀和
LL sum[N], cnt[N], inv[N];
int lowbit(int x) {
return x & -x;
}
void update(LL bit[], int x, int delta) {
while (x <= n) {
bit[x] += delta; x += lowbit(x);
}
}
LL query(LL bit[], int x) {
LL res = 0;
while (x > 0) {
res += bit[x]; x -= lowbit(x);
}
return res;
}
int main()
{
int m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &p[i]);
f[p[i]] = query(inv, n) - query(inv, p[i]);
if (f[p[i]] > 0) {
update(sum, f[p[i]], f[p[i]]);
update(cnt, f[p[i]], 1);
}
update(inv, p[i], 1);
}
while (m--) {
int t, c; scanf("%d%d", &t, &c);
if (t == 1) {
int i = p[c] < p[c + 1] ? p[c] : p[c + 1];
// 注意不要忘了判f[i]>0
if (f[i] > 0) {
update(sum, f[i], -f[i]);
update(cnt, f[i], -1);
}
f[i] += p[c] < p[c + 1] ? 1 : -1;
if (f[i] > 0) {
update(sum, f[i], f[i]);
update(cnt, f[i], 1);
}
swap(p[c], p[c + 1]);
} else {
c = min(c, n - 1); // 冒泡排序n-1轮过后足够完成排序
LL ans = query(sum, n) - query(sum, c) - (query(cnt, n) - query(cnt, c)) * c;
printf("%lld\n", ans);
}
}
return 0;
}
习题:P4648 [IOI 2007] pairs 动物对数
解题思路
情况一:\(B = 1\)(一维空间)
问题:在一条直线上,给定 \(N\) 个点,找出所有距离小于等于 \(D\) 的点对。
解题思路:
- 排序:首先,将所有 \(N\) 个点的坐标从小到大进行排序。
- 双指针:遍历排序后的每一个点 \(x_i\),对于每个 \(x_i\),想找到有多少个在它之前(即坐标更小)的点 \(x_j\) 满足 \(x_i - x_j \le D\)。
- 使用一个指针 \(j\),它指向满足条件的点中坐标最小的那个。当 \(i\) 向右移动时,\(j\) 也会向右移动,不可能后退。
- 对于当前的 \(i\),移动 \(j\) 直到 \(x_j\) 刚好满足 \(x_i - x_j \le D\)。那么,所有在 \(j\) 和 \(i\) 之间的点(不包括 \(i\))都满足条件。这样的点的数量就是 \(i-j\)。
- 将这个数量累加到总答案中。遍历完所有 \(i\) 后,就得到了最终结果。
情况二:\(B = 2\)(二维空间)
问题:在一个平面上,给定 \(N\) 个点,找出所有曼哈顿距离(\(|x_1 - x_2| + |y_1 - y_2|\))小于等于 \(D\) 的点对。
解题思路:
- 坐标变换:直接处理曼哈顿距离 \(|x_1 - x_2| + |y_1 - y_2| \le D\) 比较复杂。使用一个巧妙的技巧:将坐标系旋转 \(45\) 度。令新坐标为 \(u = x + y\) 和 \(v = x - y\)。经过变换后,原来的曼哈顿距离条件就等价于新坐标系下的切比雪夫距离条件:\(\max (|u_1 - u_2|, |v_1 - v_2|) \le D\)。这又等价于 \(|u_1 - u_2| \le D\) 和 \(|v_1 - v_2| \le D\) 两个不等式同时成立。
- 问题转化为了:对于每个点 \((u_i, v_i)\),寻找有多少个其他的点 \((u_j, v_j)\) 满足 \(u_i - D \le u_j \le u_i + D\) 且 \(v_i - D \le v_j \le v_i + D\)。这是一个经典的二维数点问题。
- 将所有点按 \(u\) 排序。
- 从左到右遍历每个点 \(p_i\)(按 \(u\) 坐标)。
- 使用双指针 \(j\) 维护一个“活动窗口”,确保窗口内所有点的 \(u\) 坐标都满足 \(u_i - u_j \le D\)。对于 \(u\) 坐标太小的点(即 \(u_j \lt u_i - D\)),将其从窗口中移除。
- 对于在窗口内的点,需要快速统计有多少个点的 \(v\) 坐标落在 \([v_i - D, v_i + D]\) 区间内。这个任务可以通过树状数组高效完成。
- 在处理点 \(p_i\) 时,先将不满足 \(u\) 坐标条件的点从树状数组中删除,然后查询树状数组中满足 \(v\) 坐标条件的点的数量,计入总答案。最后,将当前点 \(p_i\) 的 \(v\) 坐标加入树状数组。
情况三:\(B = 3\)(三维空间)
问题:在三维空间中,给定 \(N\) 个点,找出所有曼哈顿距离(\(|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|\))小于等于 \(D\) 的点对。
解题思路:
- 利用数据范围:这一问的关键在于题目给出的坐标范围非常小(\(M \le 75\))。
- 坐标变换 + 降维打击:类似于二维情况,对 \(x,y\) 坐标进行变换:\(u = x + y, v = x - y\)。距离条件变为 \(\max (|u_1 - u_2|, |v_1 - v_2|) + |z_1 - z_2| \le D\)。
- 分层处理 + 二维前缀和:
- 可以把三维空间看成是按 \(z\) 坐标分成的很多个独立的二维 \((u,v)\) 平面。
- 由于 \(u,v,z\) 的坐标范围都很小,可以创建一个三维数组 \(sum_{z, u, v}\) 来记录每个坐标上的点的数量。
- 对每个 \(z\) 平面,预处理出它的二维前缀和。这样,就可以在 \(O(1)\) 时间内查询出任意一个矩形区域 \((u_1,v_1)\) 到 \((u_2,v_2)\) 内点的总数。
- 分类统计:遍历每一个点 \(p_i = (u_i, v_i, z_i)\),计算能与它配对的点数。
- 对于和 \(p_i\) 在同一个 \(z\) 平面内的点 \(p_j\),它们 \(z\) 坐标的距离为 \(0\)。所以 \(p_j\) 必须满足 \(\max(|u_i - u_j|, |v_i - v_j|) \le D\)。利用处理好的二维前缀和,可以快速查出在 \(z_i\) 平面上,以 \((u_i,v_i)\) 为中心、范围为 \(D\) 的正方形内有多少个点。
- 对于在不同 \(z\) 平面内的点 \(p_j\),设 \(z\) 方向的距离为 \(d_z = |z_i - z_j|\),那么 \(p_j\) 必须满足 \(\max(|u_i-u_j|,|v_i-v_j|) \le D-d_z\)。遍历所有 \(z_j\) 不等于 \(z_i\) 的平面,利用二维前缀和计算出每个平面上满足条件的点的数量,然后累加起来。
- 去重:在统计时,为了避免重复计数(例如 \((A,B)\) 和 \((B,A)\) 被算作两对),对同一平面的点对数最后除以 \(2\),对不同平面的点对只计算 \(z_j \lt z_i\) 的情况。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 100005;
int b, n, d, m;
int lowbit(int x) {
return x & -x;
}
namespace b1 {
int x[MAXN];
void solve() {
for (int i = 1; i <= n; i++) scanf("%d", &x[i]);
sort(x + 1, x + n + 1);
LL ans = 0;
int j = 1;
for (int i = 1; i <= n; i++) {
while (j < i && x[j] + d < x[i]) j++;
ans += i - j;
}
printf("%lld\n", ans);
}
};
namespace b2 {
struct Point {
int x, y;
bool operator<(const Point& other) const {
return x < other.x;
}
} p[MAXN];
LL c[MAXN * 3];
void update(int x, int d) {
while (x < MAXN * 3) {
c[x] += d;
x += lowbit(x);
}
}
LL query(int x) {
if (x <= 0) return 0;
if (x >= MAXN * 3) return c[MAXN * 3 - 1];
LL ret = 0;
while (x > 0) {
ret += c[x];
x -= lowbit(x);
}
return ret;
}
void solve() {
for (int i = 1; i <= n; i++) {
int x, y;
scanf("%d%d", &x, &y);
p[i].x = x + y + MAXN; p[i].y = x - y + MAXN;
}
sort(p + 1, p + n + 1);
LL ans = 0;
int j = 1;
for (int i = 1; i <= n; i++) {
while (j < i && p[j].x + d < p[i].x) {
update(p[j].y, -1);
j++;
}
ans += query(p[i].y + d) - query(p[i].y - d - 1);
update(p[i].y, 1);
}
printf("%lld\n", ans);
}
};
namespace b3 {
struct Point {
int x, y, z;
} p[MAXN];
LL sum[100][300][300];
LL query(int z, int x, int y) {
if (x <= 0 || y <= 0) return 0;
if (x >= 300) x = 299;
if (y >= 300) y = 299;
return sum[z][x][y];
}
LL calc(int z, int x, int y, int d) {
return query(z, x + d, y + d) - query(z, x - d - 1, y + d) - query(z, x + d, y - d - 1) + query(z, x - d - 1, y - d - 1);
}
void solve() {
for (int i = 1; i <= n; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
p[i].x = x + y + 100; p[i].y = x - y + 100; p[i].z = z;
sum[p[i].z][p[i].x][p[i].y]++;
}
for (int i = 1; i <= 75; i++)
for (int j = 1; j < 300; j++)
for (int k = 1; k < 300; k++)
sum[i][j][k] += sum[i][j - 1][k] + sum[i][j][k - 1] - sum[i][j - 1][k - 1];
LL ans1 = 0, ans2 = 0;
for (int i = 1; i <= n; i++) {
for (int j = max(p[i].z - d, 1); j < p[i].z; j++) ans1 += calc(j, p[i].x, p[i].y, d - p[i].z + j);
ans2 += calc(p[i].z, p[i].x, p[i].y, d) - 1;
}
printf("%lld\n", ans1 + ans2 / 2);
}
};
int main()
{
scanf("%d%d%d%d", &b, &n, &d, &m);
if (b == 1) b1::solve();
else if (b == 2) b2::solve();
else b3::solve();
return 0;
}
习题:P3586 [POI 2015 R2] 物流 Logistics
解题思路
本题的难点在于如何高效地判断 Z c s 询问。
一个 Z c s 询问,实际上是在问:当前拥有的“资源”是否足够支撑 \(s\) 次“消耗”,每次消耗需要从 \(c\) 个正数中各取走 1。
分析一次操作能持续 \(s\) 次的条件。
- 对于序列中一个数 \(a_i\),如果 \(a_i \ge s\),那么它在每次操作中都可以被选中,总共可以被选中 \(s\) 次。
- 如果一个数 \(a_i \lt s\),那么它最多只能被选中 \(a_i\) 次,之后就会变为非正数,不能再被选中。
可以从“可被选中的次数”这个角度来思考。
- 所有值大于等于 \(s\) 的数,可以认为是“无限”资源,因为它们至少能满足这 \(s\) 次操作的需求,假设有 \(\text{count}_{\ge s}\) 个这样的数。
- 所有值小于 \(s\) 的数,是“有限”资源。它们总共能提供的可被选中的次数就是它们的值的总和,即 \(\text{sum}_{\lt s}\)。
在每一次操作中,都需要选出 \(c\) 个数。
- 可以优先选择那 \(\text{count}_{\ge s}\) 个值大于等于 \(s\) 的数。
- 如果 \(c \gt \text{count}_{\ge s}\),那么每次操作还需要额外从值小于 \(s\) 的数中选出 \(c - \text{count}_{\ge s}\) 个。
- 在 \(s\) 次操作中,总共需要从值小于 \(s\) 的数中选出 \((c - \text{count}_{\ge s}) \times s\) 次。
- 值小于 \(s\) 的数总共能提供的被选次数为 \(\text{sum}_{\lt s}\)。
- 因此,必须满足 \(\text{sum}_{\lt s} \ge (c - \text{count}_{\ge s}) \times s\)。
整理这个不等式得到 \(\text{sum}_{\lt s} + \text{count}_{\ge s} \times s \ge c \times s\),这就是判断 Z c s 询问的核心条件。
参考代码
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
using ll = long long;
const int N = 1e6 + 5;
// 树状数组模板:lowbit 函数
int lowbit(int x) {
return x & -x;
}
// 存储操作的结构体
struct Operation {
char type;
int p1, p2;
};
int n, m;
int a[N]; // 存储序列的当前值,a[k] 表示第 k 个数的值
Operation ops[N]; // 存储所有 m 个操作
vector<int> vals; // 用于离散化,存储所有出现过的值以及查询的阈值 s
// 树状数组 (BIT) 结构体
struct BIT {
int bound; // 树状数组的大小,即离散化后不同值的数量
ll c[N]; // 树状数组本体
// 单点更新:在 idx 位置增加 delta
void update(int idx, ll delta) {
while (idx <= bound) {
c[idx] += delta;
idx += lowbit(idx);
}
}
// 前缀查询:查询 [1, idx] 区间的和
ll query(int idx) {
ll sum = 0;
while (idx > 0) {
sum += c[idx];
idx -= lowbit(idx);
}
return sum;
}
};
BIT cnt, sum; // cnt: 维护数量的BIT; sum: 维护和的BIT
// 将原始值 x 映射到其在离散化数组 vals 中的 1-based 索引
int val_to_idx(int x) {
// lower_bound 找到第一个不小于 x 的元素的位置
return lower_bound(vals.begin(), vals.end(), x) - vals.begin() + 1;
}
int main()
{
cin >> n >> m;
// 读入所有操作,并收集所有需要离散化的值
for (int i = 0; i < m; i++) {
cin >> ops[i].type >> ops[i].p1 >> ops[i].p2;
// 对于 U k a, p2 是 a; 对于 Z c s, p2 是 s
vals.push_back(ops[i].p2);
}
vals.push_back(0); // 加入初始值 0
// 离散化:排序并去重
sort(vals.begin(), vals.end());
vals.erase(unique(vals.begin(), vals.end()), vals.end());
// 初始化树状数组
cnt.bound = sum.bound = vals.size();
// 初始时,有 n 个 0
cnt.update(val_to_idx(0), n);
// 初始和为 0,无需更新 sum BIT
// 依次处理每个操作
for (int i = 0; i < m; i++) {
if (ops[i].type == 'U') { // 修改操作
int k = ops[i].p1;
int a_new = ops[i].p2;
int a_old = a[k];
if (a_new == a_old) continue; // 值未改变,无需操作
// 获取新旧值对应的离散化索引
int idx_new = val_to_idx(a_new);
int idx_old = val_to_idx(a_old);
// 在BIT中移除旧值的贡献
cnt.update(idx_old, -1);
sum.update(idx_old, -a_old);
// 在BIT中加入新值的贡献
cnt.update(idx_new, 1);
sum.update(idx_new, a_new);
a[k] = a_new; // 更新序列数组
} else { // 查询操作
int c = ops[i].p1;
int s = ops[i].p2;
// 找到阈值 s 对应的离散化索引
int idx_s = val_to_idx(s);
// 查询所有值 < s 的元素的和与数量
// query(idx_s - 1) 查询的是离散化索引严格小于 idx_s 的所有值
ll sum_lt_s = sum.query(idx_s - 1);
int cnt_lt_s = cnt.query(idx_s - 1);
// 计算值 >= s 的元素的数量
int cnt_ge_s = n - cnt_lt_s;
// 检查核心条件: sum_lt_s + s * count_ge_s >= c * s
// 使用 1ll 将部分计算提升到 long long,防止溢出
if (1ll * s * cnt_ge_s + sum_lt_s >= 1ll * c * s) {
cout << "TAK\n";
} else {
cout << "NIE\n";
}
}
}
return 0;
}
例题:P1972 [SDOI2009] HH 的项链
给定一个长度为 \(n\) 的序列 \(a\),有 \(m\) 次询问。每次询问给定一个区间 \([l,r]\),要求回答该区间内有多少个不同的数字。
\(1 \le n,m,a_i \le 10^6\)
本题是经典的静态区间不同数个数查询问题。
由于查询是“静态”的(即序列本身不会被修改),可以不按输入顺序顺序回答查询,而是将所有查询离线下来,以一种更优的顺序处理。
问题的核心在于如何不重复地计数,对于区间 \([l,r]\) 内的每一种数字,只计数一次。一个巧妙的约定是:对于任意一种数字,只计数其在查询区间内最靠右的那一次出现。
基于这个思想,可以将问题转化为:
对于查询 \([l,r]\),求区间 \([l,r]\) 内有多少个位置 \(i\),满足 \(a_i\) 是其值在 \([1,r]\) 这个前缀区间内的最后一次出现。
这个转化非常关键,为了高效实现,可以将所有查询按右端点 \(r\) 排序,然后从左到右扫描整个序列,同时处理所有以当前位置为右端点的查询。
对于每个查询,使用一个指针 \(p\) 将扫描过程推进到 \(r\),并用一个树状数组来维护信息。树状数组维护的是推进过程中每个位置是否有效的前缀和,这里假设 1 代表有效,0 代表无效。有效的定义是在扫描到 \(p\) 时,如果某个位置 \(i\) 有效,代表 \(a_i\) 是其值在 \([1, p]\) 这个前缀区间中最后一次出现的位置。
因此在推进过程中,如果当前元素 \(a_p\) 之前出现过,说明其上一次出现的位置不再是其值的“最右出现位置”,在树状数组中将其“无效化”,而当前位置 \(p\) 成为了 \(a_p\) 新的“最右出现位置”,在树状数组中将其“有效化”。
当 \(p\) 推进到 \(r\) 之后,树状数组的状态正好反映了前缀 \([1,r]\) 的情况。此时,查询 \([l,r]\) 的答案,就是树状数组在 \([l,r]\) 区间内“有效”位置的数量,这个数量可以通过树状数组的前缀和性质求得。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1e6 + 5;
int n, m, a[N], ans[N];
int last[N]; // last[v] 存储值 v 最后出现的位置
int bit[N]; // 树状数组
int lowbit(int x) {
return x & -x;
}
// 更新操作:在 idx 位置增加 val
void update(int idx, int val) {
while (idx <= n) {
bit[idx] += val;
idx += lowbit(idx);
}
}
// 查询操作:查询 [1, idx] 区间的前缀和
int query(int idx) {
int sum = 0;
while (idx > 0) {
sum += bit[idx];
idx -= lowbit(idx);
}
return sum;
}
// 定义查询结构体
struct Query {
int l, r, id;
};
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
scanf("%d", &m);
vector<Query> q(m);
for (int i = 0; i < m; i++) {
scanf("%d%d", &q[i].l, &q[i].r);
q[i].id = i;
}
// 按右端点对查询进行排序
sort(q.begin(), q.end(), [](const Query& a, const Query& b) {
return a.r < b.r;
});
// 扫描序列,处理查询
int pos = 1; // 指向当前处理到的序列位置
for (int i = 0; i < m; i++) {
int l = q[i].l;
int r = q[i].r;
int id = q[i].id;
// 将 pos 推进到当前查询的右端点 r
while (pos <= r) {
// 如果 a[pos] 之前出现过
if (last[a[pos]] != 0) {
// 将其上一个位置的贡献从树状数组中移除
update(last[a[pos]], -1);
}
// 为当前位置添加贡献
update(pos, 1);
// 更新 a[pos] 的最后出现位置为 pos
last[a[pos]] = pos;
pos++;
}
// 计算查询结果
// query(r) - query(l-1) 即为区间 [l, r] 的和
// 这代表了在 [l, r] 中,其值在 [l, r] 区间内最后一次出现的位置的数量
// 这等价于 [l, r] 中不同元素的个数
ans[id] = query(r) - query(l - 1);
}
// 按原始顺序输出答案
for (int i = 0; i < m; i++) {
printf("%d\n", ans[i]);
}
return 0;
}
习题:P4113 [HEOI2012] 采花
解题思路
与 P1972 [SDOI2009] HH 的项链 类似,改成记录每种颜色最近两次出现的位置。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 2e6 + 5;
struct Query {
int l, r, id;
};
int n, c, m;
int a[N], ans[N];
int last[N][2]; // last[color] 存储颜色 color 最后两个出现的位置
int bit[N];
int lowbit(int x) {
return x & -x;
}
// 更新操作:在 idx 位置增加 val
void update(int idx, int val) {
while (idx <= n) {
bit[idx] += val;
idx += lowbit(idx);
}
}
// 查询操作:查询 [1, idx] 区间的前缀和
int query(int idx) {
int sum = 0;
while (idx > 0) {
sum += bit[idx];
idx -= lowbit(idx);
}
return sum;
}
int main()
{
scanf("%d%d%d", &n, &c, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
vector<Query> q(m);
for (int i = 0; i < m; i++) {
scanf("%d%d", &q[i].l, &q[i].r);
q[i].id = i;
}
// 按右端点对查询进行排序
sort(q.begin(), q.end(), [](const Query &a, const Query &b) {
return a.r < b.r;
});
// 扫描序列,处理查询
int p = 1; // 指向当前处理到的序列位置
for (int i = 0; i < m; i++) {
int l = q[i].l;
int r = q[i].r;
int id = q[i].id;
// 将 p 推进到当前查询的右端点 r
while (p <= r) {
// p1 是 a[p] 上次出现的位置
int p1 = last[a[p]][0];
// p2 是 a[p] 上上次出现的位置
int p2 = last[a[p]][1];
// 如果 p1 存在,说明当前是第二次或更多次出现
if (p1 > 0) {
// 在 p1 位置增加一个贡献,代表颜色 a[p] 满足“出现两次”的条件
update(p1, 1);
// 如果 p2 存在,说明当前是第三次或更多次出现
// 那么 p2 位置的贡献是“过时”的,需要移除
if (p2 > 0) {
update(p2, -1);
}
}
// 更新 a[p] 上次出现的位置
last[a[p]][1] = last[a[p]][0];
last[a[p]][0] = p;
p++;
}
// 计算查询结果
// query(r) - query(l - 1) 得到的是在 [l, r] 区间内有多少个“满足两次”的标记点
ans[id] = query(r) - query(l - 1);
}
// 按原始顺序输出答案
for (int i = 0; i < m; ++i) {
printf("%d\n", ans[i]);
}
return 0;
}
树状数组优化 DP
如果将树状数组代码中的求和改为取 max 或取 min,则树状数组可以用来维护前缀最大或最小值,从而帮助优化一些 DP 问题。
例题:P3431 [POI 2005] AUT-The Bus
在一个二维平面上给定 \(k\) 个点,每个点有一个坐标 \((x, y)\) 以及点权 \(p\),从左下角 \((1,1)\) 走到右上角 \((n,m)\),只能向上或向右走,求经过的点权和的最大值,\(k \le 10^5\)。
解题思路
若某个点为点 \(i\),设 \(dp_i\) 表示 \((1,1)\) 到 \((x_i, y_i)\) 点权和的最大值,则有 \(dp_i = \max \{ dp_j \} + p_i\),其中点 \(j\) 需要满足 \(x_j \le x_i\) 并且 \(y_j \le y_i\),也就是点 \(j\) 在点 \(i\) 的左下方。
为了保证计算某个点 \(i\) 时其左下方的所有点都已计算过,可以对输入的点以横坐标为第一关键字,纵坐标为第二关键字进行排序,则排序后按顺序扫描即满足之前的点一定是在左边的。此时要求出该点下方(即 \(y_j \le y_i\))的 \(dp_j\) 的最大值,正好是一个前缀最大值,所以可以用树状数组来维护。
时间复杂度 \(O(k \log k)\)。
参考代码
#include <cstdio>
#include <algorithm>
#include <vector>
using ll = long long;
const int K = 100005;
struct Point {
int x, y, p;
};
Point a[K];
int k;
ll c[K], dp[K];
std::vector<int> num;
int discretize(int x) {
return std::lower_bound(num.begin(), num.end(), x) - num.begin() + 1;
}
int lowbit(int x) {
return x & -x;
}
void update(int x, ll val) {
while (x <= k) {
c[x] = std::max(c[x], val);
x += lowbit(x);
}
}
ll query(int x) {
ll res = 0;
while (x > 0) {
res = std::max(res, c[x]);
x -= lowbit(x);
}
return res;
}
int main()
{
int n, m; scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= k; i++) {
scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].p);
num.push_back(a[i].y);
}
std::sort(num.begin(), num.end());
num.erase(std::unique(num.begin(), num.end()), num.end());
std::sort(a + 1, a + k + 1, [](const Point& lhs, const Point& rhs) {
return lhs.x != rhs.x ? lhs.x < rhs.x : lhs.y < rhs.y;
});
ll ans = 0;
for (int i = 1; i <= k; i++) {
a[i].y = discretize(a[i].y);
dp[i] = query(a[i].y) + a[i].p;
ans = std::max(ans, dp[i]);
update(a[i].y, dp[i]);
}
printf("%lld\n", ans);
return 0;
}
习题:P6007 [USACO20JAN] Springboards G
在一个二维平面上给定 \(p\) 对点,每对点有坐标 \((x_1, y_1)\) 和 \((x_2, y_2)\),表示从前者可以不需要行走瞬移到后者,从左下角 \((0,0)\) 走到右上角 \((n,n)\),只能向上或向右走,求最小的行走距离,\(p \le 10^5\)。
解题思路
设到点 \(i\) 的最小行走距离是 \(dp_i\),则有 \(dp_i = \min \{ dp_j + x_i - x_j + y_i - y_j \}\),其中 \(j\) 在 \(i\) 的左下方。在计算 \(dp_i\) 时,\(x_i\) 和 \(y_i\) 是两个定值,可以拆到括号外面,也就是 \(dp_i = \min \{ dp_j - x_j - y_j \} + x_i + y_i\),于是和上一题类似,只不过相当于需要维护 \(dp - x - y\) 的最小值。
而如果点 \(i\) 是跳板的右上端点,还有一种情况是 \(dp_i = dp_j\),这里的点 \(j\) 指的是该跳板的左下端点。
为了在点排序后能维持之前的跳板关系,可以使用索引排序。
时间复杂度 \(O(p \log p)\)。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
using ll = long long;
const int P = 200005;
int n, p, x[P], y[P], idx[P], from[P];
ll c[P], dp[P];
std::vector<int> num;
int discretize(int x) {
return std::lower_bound(num.begin(), num.end(), x) - num.begin() + 1;
}
int lowbit(int x) {
return x & -x;
}
void update(int x, ll val) {
while (x <= 2 * p) {
c[x] = std::min(c[x], val);
x += lowbit(x);
}
}
ll query(int x) {
ll res = 2 * n;
while (x > 0) {
res = std::min(res, c[x]);
x -= lowbit(x);
}
return res;
}
int main()
{
scanf("%d%d", &n, &p);
for (int i = 1; i <= p; i++) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
x[i] = x1; y[i] = y1;
x[i + p] = x2; y[i + p] = y2; from[i + p] = i;
num.push_back(y1); num.push_back(y2);
idx[i] = i; idx[i + p] = i + p;
}
std::sort(num.begin(), num.end());
num.erase(std::unique(num.begin(), num.end()), num.end());
std::sort(idx + 1, idx + 2 * p + 1, [](int i, int j) {
return x[i] != x[j] ? x[i] < x[j] : y[i] < y[j];
});
for (int i = 1; i <= 2 * p; i++) c[i] = 2 * n;
ll ans = 2 * n;
for (int i = 1; i <= 2 * p; i++) {
int cur = idx[i];
if (x[cur] > n || y[cur] > n) continue;
dp[cur] = x[cur] + y[cur]; // 从(0,0)直接走过来
int d = discretize(y[cur]);
dp[cur] = std::min(dp[cur], query(d) + x[cur] + y[cur]);
if (from[cur] != 0) { // 如果是某个跳板的右上端点
dp[cur] = std::min(dp[cur], dp[from[cur]]);
}
ans = std::min(ans, n - x[cur] + n - y[cur] + dp[cur]);
update(d, dp[cur] - x[cur] - y[cur]);
}
printf("%lld\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号