双端队列与单调队列
双端队列
双端队列是一种具有队列和栈性质的数据结构,它能在两端进行插入和删除,而且也只能在两端插入和删除。
STL 中的双端队列可以用 deque,头文件为 <deque>,它的用法如下:
dq[i]返回队列中下标为 i 的元素dq.front()返回队头dq.back()返回队尾dq.pop_back()删除队尾,不返回值dq.pop_front()删除队头,不返回值dq.push_back(x)在队尾添加一个元素 xdq.push_front(x)在队头添加一个元素 x
当然双端队列也可以手写,如果不需要 push_front 下标可以直接从 \(0\) 开始用,用 st 表示队首位置,ed 表示队尾位置(假设队列中元素位置为 st~ed-1),push_back 相当于 q[ed++]=x,pop_back 相当于 ed--,取队尾相当于 q[ed-1],取队首相当于 q[st],pop_front 相当于 st++,这些操作时间复杂度都是 \(O(1)\) 的。注意,对于双端队列的 pop_front 来说,需要 \(O(1)\) 的时间复杂度,而 vector 的 pop_front 时间复杂度是 \(O(n)\) 的,因此不能用 vector 来实现。而如果手写的场景需要 push_front,可以从中间的数组下标开始用,在刚开始把队首和队尾放在中间,这样就可以往两边拓展了,相当于整体偏移,push_front 相当于 q[--st]=x。
std::deque 底层原理
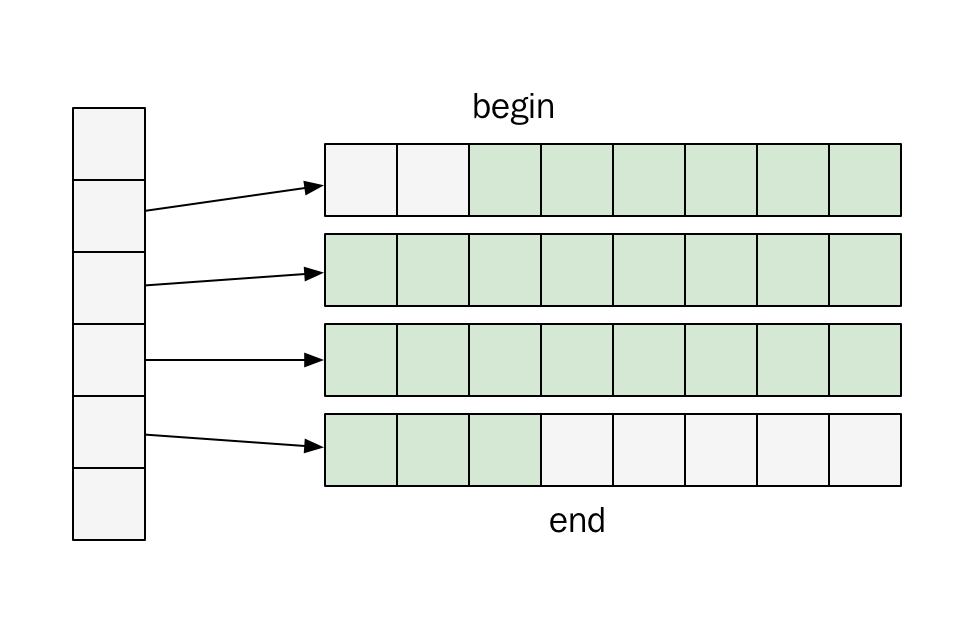
deque 底层的机制实际上是由一段一段的定量连续空间组成,因此在算法竞赛中针对 deque 有一个需要注意的点是:哪怕 deque 中只添加了一个元素,其实际还是需要消耗“一段”的内存,因此当题目中需要很多双端队列时建议用 STL 中的 list,list 本质上就是双向链表,除了不支持下标访问以外,其头尾操作的用法与 deque 一样,而双向链表显然可以模拟双端队列的操作。
例题:B3656 【模板】双端队列 1
题中需要维护百万级别个双端队列,由前面的底层原理讲解可知,即便每个双端队列中只有一个元素,其消耗的内存并不只是这一百万个元素的内存消耗,还需要乘上“一段”的大小,因此本题如果使用 deque dq[N] 这样的数组会导致内存空间溢出,即 MLE,而用 STL 中的 list(双向链表)来模拟则消耗的内存包括这最多一百万个元素的消耗以及每个元素附带的前驱、后继指针,因此是符合要求的。
#include <cstdio>
#include <list>
using namespace std;
const int N = 1000005;
char op[15];
list<int> dq[N];
int main()
{
int q; scanf("%d", &q);
while (q--) {
scanf("%s", op);
int a; scanf("%d", &a);
if (op[0] == 's') {
int sz = dq[a].size();
printf("%d\n", sz);
} else if (op[0] == 'f') {
if (!dq[a].empty()) printf("%d\n", dq[a].front());
} else if (op[0] == 'b') {
if (!dq[a].empty()) printf("%d\n", dq[a].back());
} else if (op[1] == 'o') {
if (!dq[a].empty()) {
if (op[4] == 'b') dq[a].pop_back();
else dq[a].pop_front();
}
} else if (op[1] == 'u') {
int x; scanf("%d", &x);
if (op[5] == 'b') dq[a].push_back(x);
else dq[a].push_front(x);
}
}
return 0;
}
习题:P7915 [CSP-S 2021] 回文
解题思路
每一步只能从 \(\{ a \}\) 的两端之一取一个数字加到 \(\{b\}\) 的末尾,假设第一步选择了 L 操作,此时必然存在另一个 \(a_x=a_1\),而由于 \(b_1\) 对应 \(a_1\),那么 \(b_{2n}\) 就要对应 \(a_x\),即 \(a_x\) 作为 \(\{ a \}\) 中最后一个被取的。此时 \(a\) 被分成两个部分,一块是 \(a_2 \rightarrow a_{x-1}\),另一块是 \(a_{x+1} \rightarrow a_{2n}\),而下一步 \(a\) 中要取的要么是 \(a_2\) 要么是 \(a_{2n}\),由于需要构造出回文,则倒数第二次操作对应的应该是 \(a_{x-1}\) 或 \(a_{x+1}\),因此只需要分析两次操作元素的对应关系即可决定选择 L 操作还是 R 操作(显然,若两操作均不可行,说明接下来无法再操作;若只能进行其中一种操作那必然选择该操作;若两操作都可行,由于要求字典序最小,优先 L 操作)。
同理,如果第一步操作选择 R 也会有一个类似的分析过程,总体的时间复杂度为 \(O(n)\)。

#include <cstdio>
#include <deque>
using namespace std;
const int N = 1000005;
int a[N], ans[N], n; // ans[] 0: L, 1: R
deque<int> left, right;
void update(int i, int op1, int op2) {
ans[i] = op1; ans[n - i + 1] = op2;
}
bool check() {
for (int i = 2; i <= n / 2; i++) {
// try L
if (!left.empty()) {
// try L...L
if (left.size() > 1 && left.front() == left.back()) {
update(i, 0, 0); left.pop_front(); left.pop_back();
continue;
}
// try L...R
if (!right.empty() && left.front() == right.front()) {
update(i, 0, 1); left.pop_front(); right.pop_front();
continue;
}
}
// try R
if (!right.empty()) {
// try R...L
if (!left.empty() && right.back() == left.back()) {
update(i, 1, 0); right.pop_back(); left.pop_back();
continue;
}
// try R...R
if (right.size() > 1 && right.back() == right.front()) {
update(i, 1, 1); right.pop_back(); right.pop_front();
continue;
}
}
return false;
}
return true;
}
void print_ans() {
for (int i = 1; i <= n; i++) printf("%c", "LR"[ans[i]]);
printf("\n");
}
int main()
{
int t; scanf("%d", &t);
while (t--) {
scanf("%d", &n); n *= 2;
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
// first L
// find the element == a[1] and split into two parts
left.clear(); right.clear();
int idx = 1; update(1, 0, 0);
for (int i = 2; i <= n; i++) {
if (a[i] == a[1]) idx = i;
else if (idx == 1) left.push_back(a[i]);
else right.push_back(a[i]);
}
if (check()) {
print_ans(); continue;
}
// first R
left.clear(); right.clear(); idx = n; update(1, 1, 0);
for (int i = 1; i < n; i++) {
if (a[i] == a[n]) idx = i;
else if (idx == n) left.push_back(a[i]);
else right.push_back(a[i]);
}
if (check()) print_ans();
else printf("-1\n");
}
return 0;
}
单调队列
单调队列是一种内部元素具有单调性的队列,当区间的左右端点都单调递增变化时,可以用单调队列维护“区间内最值”。
被单调队列了。
这句话经常在有人比你小又比你强时使用。这是一个非常形象的比喻,以单调队列维护区间最大值为例,如果有个数 \(a_i\) 在 \(a_j\) 后面,并且 \(a_i > a_j\),那么当区间包含 \(a_i\) 时,\(a_j\) 就再也不可能成为区间最大值了。这就是单调队列维护区间最值的核心思想。
例题:P1886 滑动窗口 /【模板】单调队列
分析:暴力枚举的方式是进行 \(n-k\) 次循环,每次查找长度为 \(k\) 区间的最值,这样的算法时间复杂度是 \(O(nk)\) 的,无法通过这个题目。
以下分析以最大值为例,最小值同理。可以建立一个队列来维护这些数据,队首在左,队尾在右。首先队列为空,将元素加入到队列中。如果接下来的元素比队尾元素更大,那么将队尾元素出队,直到这个元素不大于队尾元素为止。当处理到的数据下标大于等于 \(k\),说明已经处理完了 \(k\) 个数字,可以查询这个区间的最大值了。这里的最大值就是队首元素。
在每次新加入元素之前,先要检查队首元素是否过期(不再处于需要统计的区间中):如果队首元素的下标小于等于 \(i-k\),说明队首元素过期了,此时队首元素就需要出队。
例如数据依次为 \([3,19,1,12,5,8,10,6]\),而 \(k=4\),维护过程如下:

这个队列不仅可以从队尾入队、队首出队,还可以从队尾出队(想象一个队伍在排队,排在最后的人发现后面要加入队伍的人惹不起,主动放弃了排队)。使用这种队列,保障队列内的元素具有单调性,这种队列被称为单调队列。
每个元素最多入队一次、出队一次,且出入队时间复杂度都为 \(O(1)\),因此总时间复杂度为 \(O(n)\)。
#include <cstdio>
#include <deque>
using namespace std;
const int N = 1000005;
int a[N];
int main()
{
int n, k; scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
deque<int> dq; // 单调队列中存的实际上是元素在序列中的下标
for (int i = 1; i <= n; i++) {
while (!dq.empty() && dq.front() <= i - k) dq.pop_front();
while (!dq.empty() && a[dq.back()] >= a[i]) dq.pop_back();
dq.push_back(i);
if (i >= k) printf("%d%c", a[dq.front()], i == n ? '\n' : ' ');
}
dq.clear();
for (int i = 1; i <= n; i++) {
while (!dq.empty() && dq.front() <= i - k) dq.pop_front();
while (!dq.empty() && a[dq.back()] <= a[i]) dq.pop_back();
dq.push_back(i);
if (i >= k) printf("%d%c", a[dq.front()], i == n ? '\n' : ' ');
}
return 0;
}
因为要知道队首元素是否过期,单调队列里面存储的实际上是下标而不是数据本身。
习题:P2032 扫描
解题思路
模板题,求区间长度为 \(k\) 的滑动窗口最大值。
#include <cstdio>
#include <deque>
using namespace std;
const int N = 2000005;
int a[N];
int main()
{
int n, k; scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
deque<int> dq;
for (int i = 1; i <= n; i++) {
while (!dq.empty() && dq.front() <= i - k) dq.pop_front();
while (!dq.empty() && a[dq.back()] <= a[i]) dq.pop_back();
dq.push_back(i);
if (i >= k) printf("%d\n", a[dq.front()]);
}
return 0;
}
习题:B3667 求区间所有后缀最大值的位置
解题思路
实际上区间内后缀最大值的个数就是用单调队列求滑动窗口最大值时单调队列中元素的个数。
#include <cstdio>
#include <deque>
using namespace std;
typedef unsigned long long ULL;
const int N = 1000005;
ULL a[N];
int main()
{
int n, k; scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) scanf("%llu", &a[i]);
deque<int> dq;
for (int i = 1; i <= n; i++) {
// [i-k+1, i]
while (!dq.empty() && dq.front() <= i - k) dq.pop_front();
while (!dq.empty() && a[dq.back()] <= a[i]) dq.pop_back();
dq.push_back(i);
if (i >= k) printf("%d\n", int(dq.size()));
}
return 0;
}
例题:P1714 切蛋糕
限制最大长度的最大子段和问题:在一段长为 \(n\) 的数列中,找出一个长度大于等于 \(1\) 且小于等于 \(m\) 的子段,使得它的和最大。
解题思路
回顾普通的最大子段和问题,可以用前缀和思想解决,对于第 \(i\) 个元素结尾的子段,其最大长度限定的最大子段和可以表示为 \(\max \{sum_i-sum_j\}\),其中 \(j \lt i\)。
minsum = 0;
for (int i = 1; i <= n; i++) { // 枚举右端点
ans = max(ans, sum[i] - minsum);
minsum = min(minsum, sum[i]);
}
对于本题来说,相当于改成 \(j\) 属于 \([i-m, i-1]\)。如果暴力扫描所有 \(j\) 的可能,则时间复杂度为 \(O(nm)\),无法通过题目。
注意每次的 \(sum_i\) 实际上是个定值,所以实际上是去最小化 \(sum_j\),针对 \(j\) 的取值范围,可以发现 \(j\) 实际上用到的范围依次是 \([0,0], [0,1], \dots, [0,m-1], [1,m], [2,m+1], [3,m+2], [4,m+3], \dots\)。因此用单调队列维护一个滑动窗口的最小值即可,每个点只会进出各一次,最终时间复杂度 \(O(n)\)。实现时有两种方法,可以先完成这次的计算,再放 \(i\),也可以在 \(i\) 来的时候,把 \(i-1\) 放进去,再进行计算。
参考代码
#include <cstdio>
#include <deque>
using namespace std;
const int N = 500005;
const int INF = 1e8;
int p[N], sum[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &p[i]); sum[i] = sum[i - 1] + p[i];
}
deque<int> dq;
dq.push_back(0);
int ans = -INF;
for (int i = 1; i <= n; i++) {
while (!dq.empty() && dq.front() < i - m) dq.pop_front();
ans = max(ans, sum[i] - sum[dq.front()]);
while (!dq.empty() && sum[dq.back()] >= sum[i]) dq.pop_back();
dq.push_back(i);
}
printf("%d\n", ans);
return 0;
}
习题:P2216 [HAOI2007] 理想的正方形
有一个 \(a \times b\) 的整数组成的矩阵,现请你从中找出一个 \(n \times n\) 的正方形区域,使得该区域所有数中的最大值和最小值的差最小。
保证 \(2 \le a,b \le 1000, n \le a, n \le b, n \le 100\),矩阵的元素均为不超过 \(10^9\) 的非负整数。
解题思路
分析:暴力枚举的方式是枚举所有符合要求的小正方形,每次在正方形中查找最小最大值并统计,这样时间复杂度是 \(O(n^2 (a-n+1)(b-n+1))\),不能通过这个题目。
如何求出一个正方形矩阵的最大值呢?可以将这个正方形的每一行数字求最大值,然后再求每一行最大值中的最大值,剩下的一个值就是这个正方形矩阵的最大值。

以样例为例,首先处理每一行,找出一行中每一个长度为 \(2\) 的区间的最大值;然后处理每一列,找到一列中每一个长度为 \(2\) 的区间的最大值。最后得到的矩阵中的一个元素就对应着一个 \(2 \times 2\) 的正方形的最大值。使用相同的方式求得每个 \(2 \times 2\) 正方形的最小值,然后遍历这两个矩阵,计算这两个数的极差并统计即得到答案。
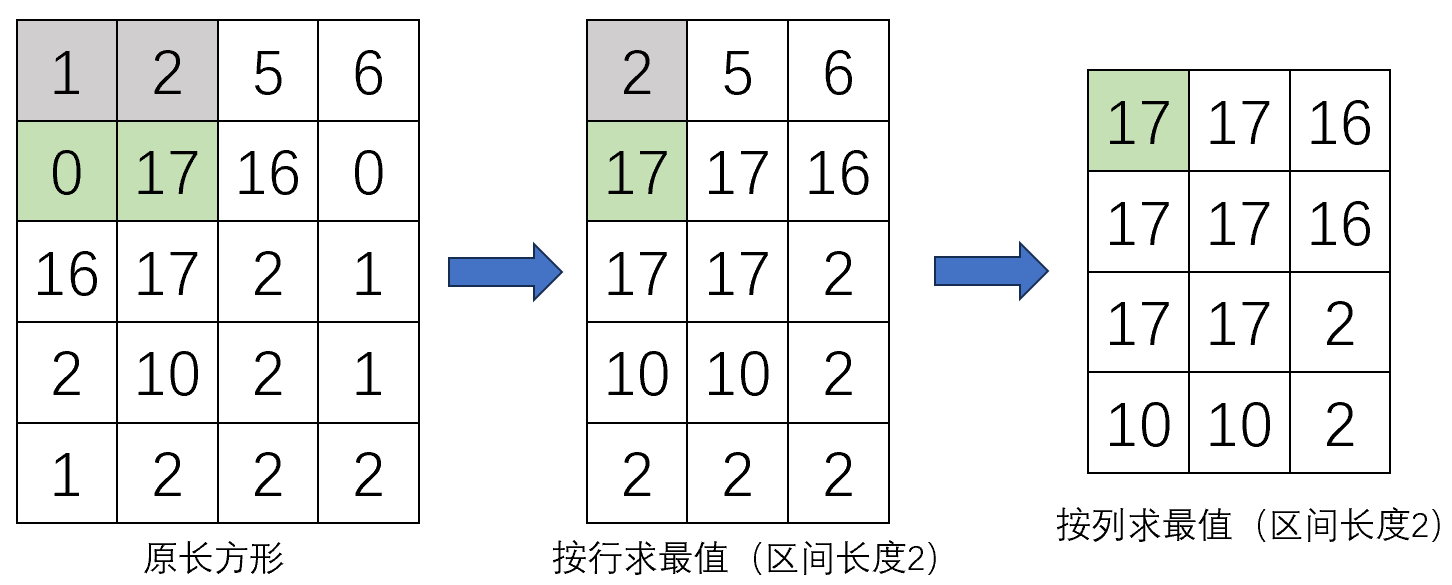
可以使用单调队列来求指定区间的最值。
参考代码
#include <cstdio>
#include <deque>
#include <algorithm>
using namespace std;
const int N = 1005;
const int INF = 1000000000;
int mat[N][N], r1[N][N], r2[N][N], mn[N][N], mx[N][N];
int main()
{
int a, b, n;
scanf("%d%d%d", &a, &b, &n);
for (int i = 1; i <= a; i++)
for (int j = 1; j <= b; j++)
scanf("%d", &mat[i][j]);
deque<int> qmin, qmax;
for (int i = 1; i <= a; i++) {
// 求每行区间最大、最小值
qmin.clear(); qmax.clear();
for (int j = 1; j < n; j++) {
while (!qmin.empty() && mat[i][qmin.back()] >= mat[i][j])
qmin.pop_back();
qmin.push_back(j);
while (!qmax.empty() && mat[i][qmax.back()] <= mat[i][j])
qmax.pop_back();
qmax.push_back(j);
}
for (int j = 1; j <= b - n + 1; j++) {
while (!qmin.empty() && qmin.front() < j)
qmin.pop_front();
while (!qmin.empty() && mat[i][qmin.back()] >= mat[i][j + n - 1])
qmin.pop_back();
qmin.push_back(j + n - 1);
r1[i][j] = mat[i][qmin.front()];
while (!qmax.empty() && qmax.front() < j)
qmax.pop_front();
while (!qmax.empty() && mat[i][qmax.back()] <= mat[i][j + n - 1])
qmax.pop_back();
qmax.push_back(j + n - 1);
r2[i][j] = mat[i][qmax.front()];
}
}
for (int i = 1; i <= b - n + 1; i++) {
// 在刚刚得到的新矩阵的基础上,求每列区间最大、最小值
qmin.clear(); qmax.clear();
for (int j = 1; j < n; j++) {
while (!qmin.empty() && r1[qmin.back()][i] >= r1[j][i])
qmin.pop_back();
qmin.push_back(j);
while (!qmax.empty() && r2[qmax.back()][i] <= r2[j][i])
qmax.pop_back();
qmax.push_back(j);
}
for (int j = 1; j <= a - n + 1; j++) {
while (!qmin.empty() && qmin.front() < j)
qmin.pop_front();
while (!qmin.empty() && r1[qmin.back()][i] >= r1[j + n - 1][i])
qmin.pop_back();
qmin.push_back(j + n - 1);
mn[j][i] = r1[qmin.front()][i];
while (!qmax.empty() && qmax.front() < j)
qmax.pop_front();
while (!qmax.empty() && r2[qmax.back()][i] <= r2[j + n - 1][i])
qmax.pop_back();
qmax.push_back(j + n - 1);
mx[j][i] = r2[qmax.front()][i];
}
}
int ans = INF;
for (int i = 1; i <= a - n + 1; i++)
for (int j = 1; j <= b - n + 1; j++)
ans = min(ans, mx[i][j] - mn[i][j]);
printf("%d\n", ans);
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号