线段树
如何快速求出一个序列的区间和?可以使用前缀和。如何快速求出一个序列的最值?可以使用 ST 表。这两种数据结构在建立的时候颇费功夫,但使用的时候效率很高。如果再增加一个需求:需要时不时修改序列的值,那么这两种数据结构就无法高效完成了。线段树可以用来解决这类问题。
线段树是一种特殊的二叉树,它可以将一个线性的序列组织成一个树状的结构,从而可以在对数时间复杂度下访问序列上的任意一个区间并进行维护。
线段树的建立与操作
例题:P3372【模板】线段树 1
已知一个数列 \(a_i\),需要支持两种操作:
1.将区间 \([x,y]\) 内每一个数加上 \(k\);
2.求出某区间 \([x,y]\) 中每一个数的和。
数的个数和操作次数不超过 \(10^5\),\(a_i, k\) 和变化后的数列数字的绝对值不超过 \(2^{63}-1\)。
分析:线段树的思想在于将序列中若干个区间在树上用节点表示,其中 \([1,n]\) 区间(\(n\) 表示序列长度)是树的根。而对一个表示区间 \([l,r]\) 的节点(\(l \ne r\)),设 \(mid=\lfloor \frac{l+r}{2} \rfloor\),将 \([l,mid]\) 和 \([mid+1,r]\) 作为该节点的左子结点和右子结点。
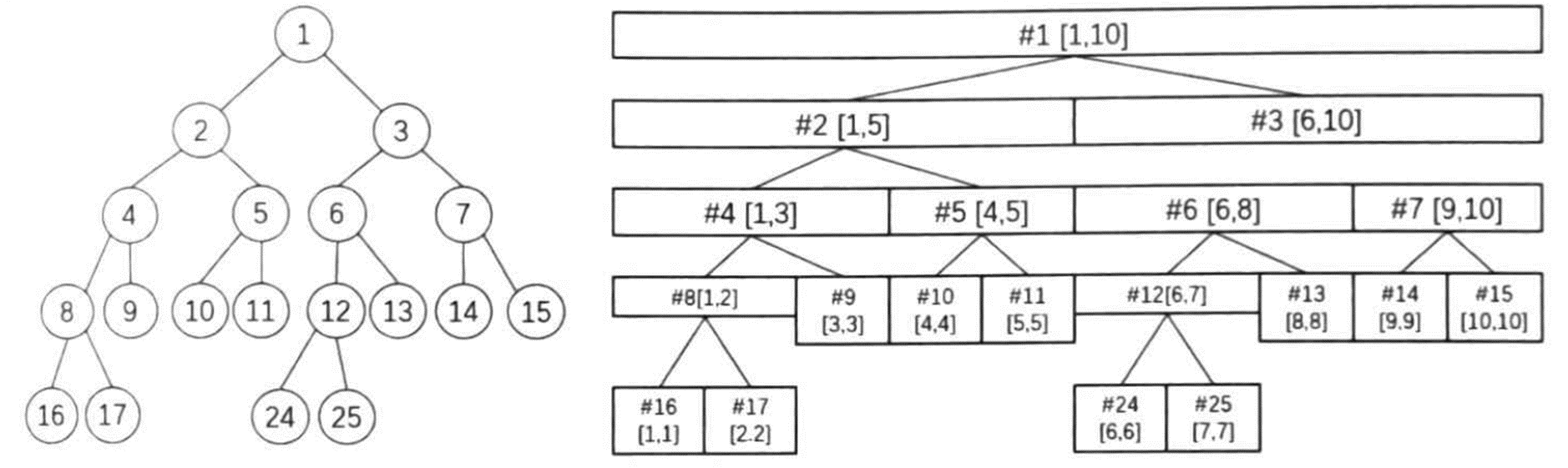
对长度为 \(10\) 的序列构建线段树,将结点 \([1,10]\) 作为根结点,设 \(mid=\lfloor \frac{1+10}{2} \rfloor = 5\),将 \([1,5]\) 作为根结点的左子结点,\([6,10]\) 作为根结点的右子结点。这两个结点的子树构建方法类似。
- 对于线段树上的任意一个结点,它要么没有子结点,要么有两个子结点,不存在只有一个子结点的情况。
- 对于一个长度为 \(n\) 的序列,它所建立的线段树只有 \(2n-1\) 个结点。
- 对于一个长度为 \(n\) 的序列,它所建立的线段树高为 \(\log n\)。
对于第二条性质,考虑首先线段树有且仅有 \(n\) 个叶结点,初始时它们没有父结点,然后将没有父结点的结点进行两两合并,每次合并会新建一个结点,共给 \(2\) 个结点建立了父结点,新增了一个没有父结点的点。也就是每次合并会新增一个结点,没有父结点的点数减一。最终线段树有且仅有一个没有父结点的结点,因此总共新建了一个 \(n-1\) 个结点,加上初始的 \(n\) 个叶结点,总共 \(2n-1\) 个结点。
对于第三条性质,考虑对于任意一个表示 \([l,r]\) 的结点,设 \(len=r-l+1\),若 \(len\) 为偶数,则显然它的两个子结点的长度均为 \(\frac{len}{2}\),若 \(len\) 为奇数,则它的一个子结点长度为 \(\frac{len+1}{2}\),另一个为 \(\frac{len-1}{2}\)。也就是说,子结点的长度至多为父结点长度加一后的一半。设树高为 \(h\),则有 \(\frac{\frac{\frac{n+1}{2}+1}{2}+1}{2} \dots\),迭代 \(h\) 次后为 \(1\)。这个式子不大于 \(\frac{n+h}{2^h}\),于是 \(\frac{n+h}{2^h} \approx 1\),解方程得到 \(h=O(\log n)\)。
线段树中一个结点上可以维护若干个所需要的信息,在访问时,将若干个结点的信息合并,就能得到任意所需区间的信息。例如,在上图中,如果希望获得区间 \([1,4]\) 的信息,只需要将结点 \([1,3]\) 和结点 \([4,4]\) 的信息合并即可。在这里需要注意的是,使用线段树所维护的信息必须具有可合并性。
例如,如果要求区间和,区间 \([1,3]\) 的和加上 \([4,4]\) 的和显然就是区间 \([1,4]\) 的和;但是简单的线段树难以直接用于维护区间众数,因为区间 \([1,12]\)(假定是一个长度为 \(12\) 的序列)的众数不一定是区间 \([1,6]\) 的众数和 \([7,12]\) 的众数中出现次数较多的。比如考察数列(3,3,1,1,1,2,3,3,4,5,5,5),区间 \([1,6]\) 的众数是出现了 \(3\) 次的 \(1\),区间 \([7,12]\) 的众数是出现了 \(3\) 次的 \(5\),但区间 \([1,12]\) 的众数却是出现了 \(4\) 次的 \(3\)。
将根结点定义为 \(1\) 号结点;对于编号为 \(i\) 的结点,它的左子结点编号为 \(2i\),右子结点编号为 \(2i+1\)。不难发现,这样每个结点都有且仅有唯一的编号与之对应,且在线段树上,结点的最大编号不超过 \(4n-1\),其中 \(n\) 是序列长度。
1. 建立线段树
树是递归定义的,因此可以用递归的方式建立线段树:如果这个区间左端点等于右端点,说明是叶子结点,其数据的值赋值为对应数列元素的值;否则将这个区间分为左右两部分,分别递归建立线段树,然后将左右两个区间的数据进行汇总(pushup)处理。
假设初始数列是 \(1,5,4,2,3\),那么建立好的线段树如下图所示,其中圆括号里的数字是这个区间的数字和。显然非叶子结点的区间数字和是其左右两子结点的区间数字和的和。
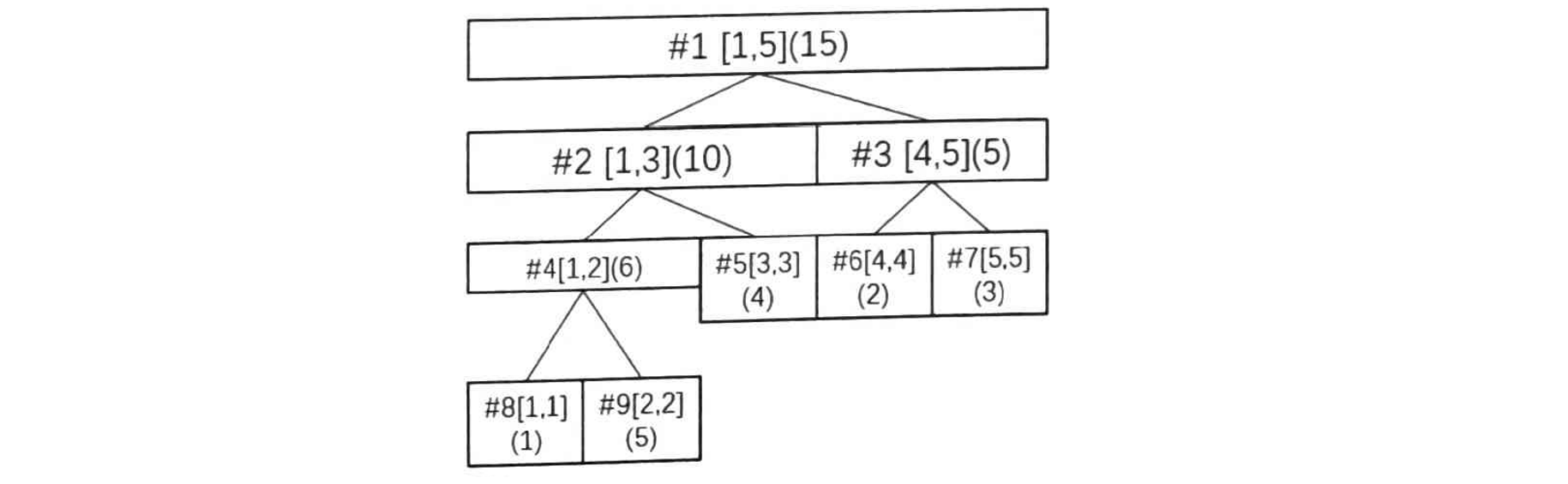
建立线段树的代码如下:
#define LC (cur*2)
#define RC (cur*2+1)
typedef long long LL;
const int MAXN = 500005;
struct Node {
int l, r; // 某个结点所代表的区间
LL value; // value存储结点对应的区间和
};
LL a[MAXN];
Node tree[MAXN*4];
void pushup(int cur) {
// 2*cur是左子结点,2*cur+1是右子结点
tree[cur].value = tree[LC].value + tree[RC].value;
}
void build(int cur, int l, int r) {
tree[cur].l = l; tree[cur].r = r;
if (l == r) { // 到达叶子结点
tree[cur].value = a[l];
return;
}
int mid = (l + r) / 2; // 将区间分成[l,mid]和[mid+1,r]
build(LC, l, mid); build(RC, mid+1, r); // 递归构建子树
pushup(cur); // 由子区间的区间和更新当前区间的和
}
在上面的代码中,cur 表示当前线段树结点的编号,成员变量 value 是结点维护的信息,也就是区间和。如果已经达到了叶结点,那么区间和显然就是对应位置的和,直接赋值即可;否则递归构建左右子树,然后通过 pushup 函数,将左右子树所维护的区间和进行合并。不难发现,每调用一次 build,就新建了一个线段树结点,因此 build 函数的时间复杂度为 \(O(n)\)。
2. 单点查询与修改
如何精确定位到叶子结点呢?假设需要定位到 \(p\) 这个结点,实际上是需要找到 \([p,p]\) 这个区间。初始时,该结点在根结点 \([1,n]\) 的子树中。根结点的左子结点为 \([1,mid]\),右子结点为 \([mid+1,n]\),其中 \(mid=(1+n)/2\),如果 \(p<=mid\),那么目标结点显然在左子树中,向左递归即可,否则目标结点在右子树中,需要向右递归。单点修改也是类似的过程,如果进行的是修改(更新操作),在返回时需要一路 pushup,来保证线段树信息的正确性。
例如将数列第 \(1\) 个数字加上 \(3\) 时,则先找到对应的叶子结点(也就是 \(8\) 号)更新它的数字,然后一直往这个结点的父结点更新区间和,直到根结点为止。
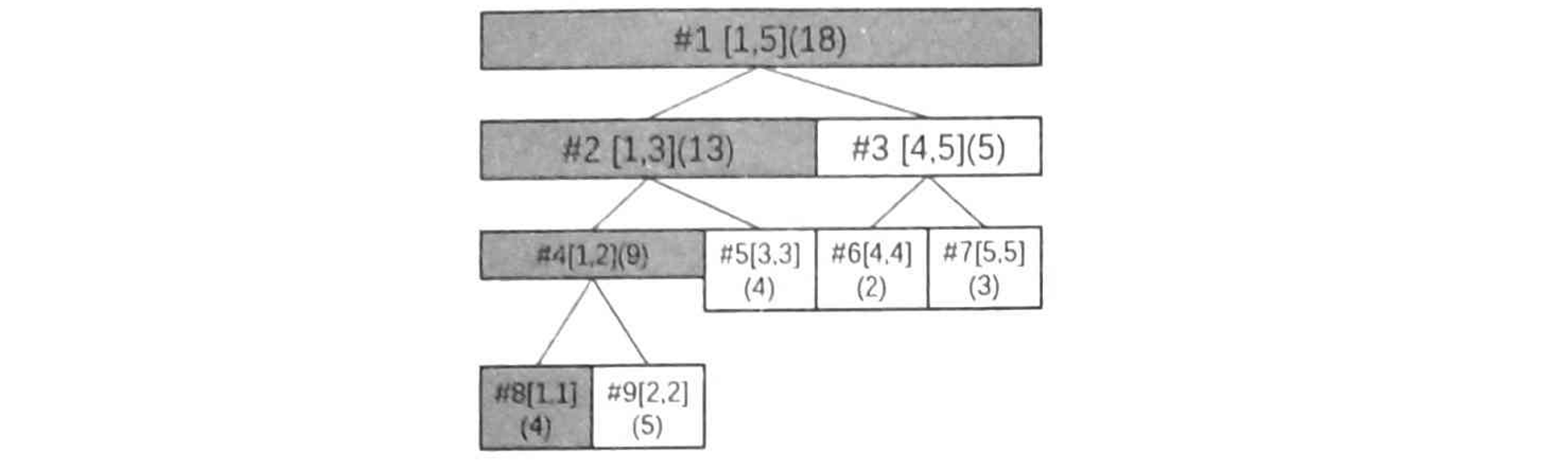
单点查询和单点修改的代码如下:
LL query1(int cur, int p) {
if (tree[cur].l == tree[cur].r) // 到达叶结点即可返回
return tree[cur].value;
int mid = (tree[cur].l + tree[cur].r) / 2;
if (p <= mid) return query1(LC, p); // 如果查询的位置在左子树内,就递归查询左子树
else return query1(RC, p); // 反之查询右子树
// 因为查询没有对区间和进行修改,因此不需要pushup
}
void update1(int cur, int p, LL x) { // 假设这里的更新操作是单点+x
if (tree[cur].l == tree[cur].r) { // 到达叶结点则直接更新
tree[cur].value += x;
return;
}
int mid = (tree[cur].l + tree[cur].r) / 2;
if (p <= mid) update1(LC, p, x); // 若修改的位置p在左子树内,递归修改左子树
else update1(RC, p, x); // 反之修改右子树
pushup(cur); // 别忘记更新以后需要修改当前结点的区间和
}
在上面的代码中,可以发现每递归调用一次函数,都会在线段树上向下移动一层。因为线段树的树高是 \(O(\log n)\),所以递归函数只会调用 \(O(\log n)\) 次。也就是说,线段树的单点操作时间复杂度为 \(O(\log n)\)。
3. 区间查询
只能支持单点操作的线段树是没什么意义的,这里我们需要用线段树快速维护区间信息,即给定区间 \([l,r]\),求这个区间的数字和。
从根开始递归,如果当前结点所代表的区间被所询问的区间 \([l,r]\) 所包含,那么直接返回当前区间的区间和;如果两个区间没有交集,应该返回 \(0\);如果没有被包含且两个区间有交,则递归左右子子结点处理即可。
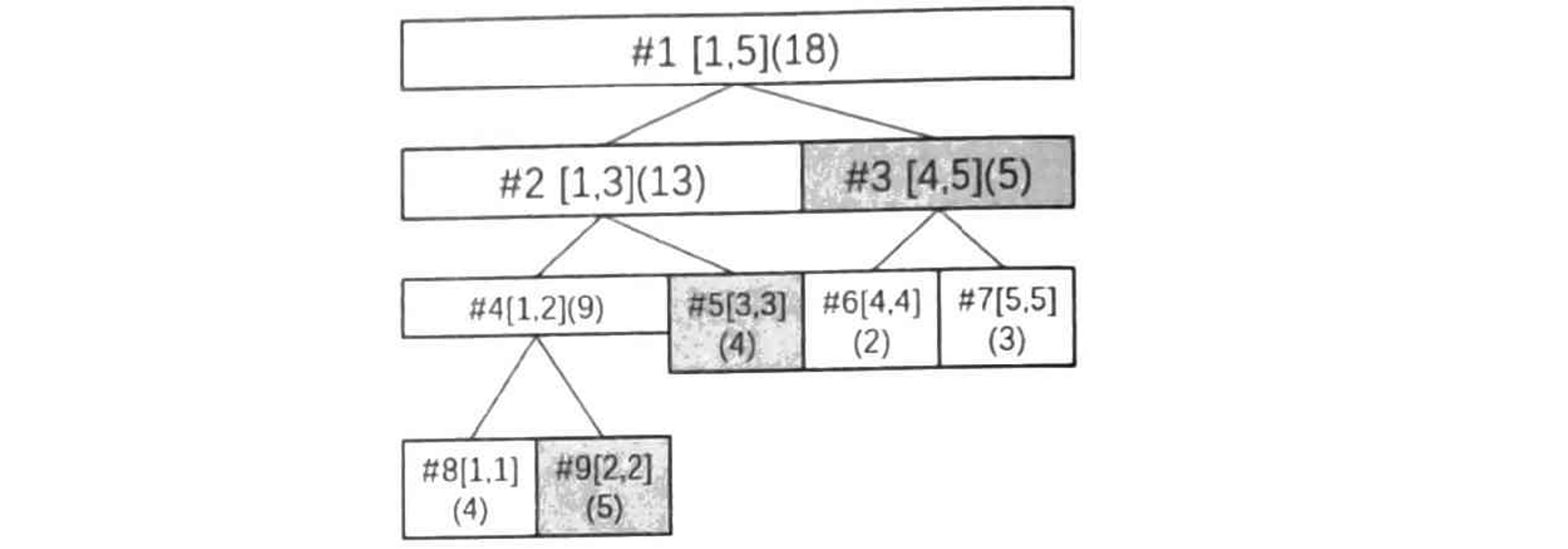
例如,查询 \([2,5]\) 的区间时,相当于查询 \([2,2],[3,3,],[4,5]\) 这些区间的数据,然后进行汇总就是答案。
区间查询的代码如下:
LL query(int cur, int l, int r) { // 区间查询
if (tree[cur].l >= l && tree[cur].r <= r) { // 如果完全包含则直接返回区间和信息
return tree[cur].value;
}
int mid = (tree[cur].l + tree[cur].r) / 2;
LL res = 0;
if (mid >= l) res += query(LC, l, r); // 查询区间与左子树区间相交
if (mid < r) res += query(RC, l, r); // 查询区间与右子树区间相交
return res;
}
在 query 函数里,并不是每层只会向下延伸一个结点,而是对左右子结点分别递归。那么如何分析其复杂度呢?在线段树每层的递归中,最多只有两个结点会向下继续递归,也就是被查询区间两端点所在的结点。而剩下的结点要么是被完全包含,要么是与查询区间不相交。因此,每一层只会新建 \(2\) 个递归函数调用。而因为树高是 \(O(\log n)\),所以总的时间复杂度还是 \(O(\log n)\)。
4. 区间修改
在区间修改时,显然不能暴力地修改每个叶子,那样效率很低。为此,引入延迟标记(又称为懒标记或者 lazy-tag),记录一些区间修改的信息。当递归至一个被完全包含的区间时,在这个区间上打一个延迟标记,记录这个区间中的每个数都需要被加上某个数,然后直接修改该结点的区间和并返回,不再向下递归。当新访问到一个结点时,先将延迟标记下放到子结点,然后再进行递归。
可以发现,这样做可以保证与根相连的某个连通块的信息总是正确的,并且在调用时总能得到正确的信息。同时,因为被完全包含和不相交的情况都不会再递归,所以其时间复杂度为 \(O(\log n)\)。
struct Node {
int l, r; // 某个结点所代表的区间
LL value, tag; // value存储结点对应的区间和
// tag是区间加的延迟标记
};
假设初始数列是 \(1,5,4,2,3\)。对区间 \([1,4]\) 的每个数都加上 \(5\),该区间在线段树上被分成了 \([1,3]\) 和 \([4,4]\) 两个结点,初始时 \([1,3]\) 的和为 \(10\),标记的值 \(tag\) 为 \(0\);\([4,4]\) 的和为 \(2\),标记的值 \(tag\) 为 \(0\)。修改时,将 \([1,3]\) 的区间和加上 \(3 \times 5 = 15\) 变成 \(25\),\([4,4]\) 的区间和加上 \(1 \times 5 = 5\) 变成 \(7\),两者的 \(tag\) 都加上 \(5\) 变成 \(5\)。完成递归后,将结点 \([1,4]\) 的区间和更新为 \(30\)。
此时如果查询 \([3,5]\) 的区间和,访问到 \([1,3]\) 区间时,发现需要继续递归下去,这时将标记下放到这个结点的两个子结点。子结点的 \(tag\) 值要增加父节点的 \(tag\) 值,同时将区间和的值加上区间长度乘以父结点的 \(tag\) 值。下放后父结点的 \(tag\) 值要清空。
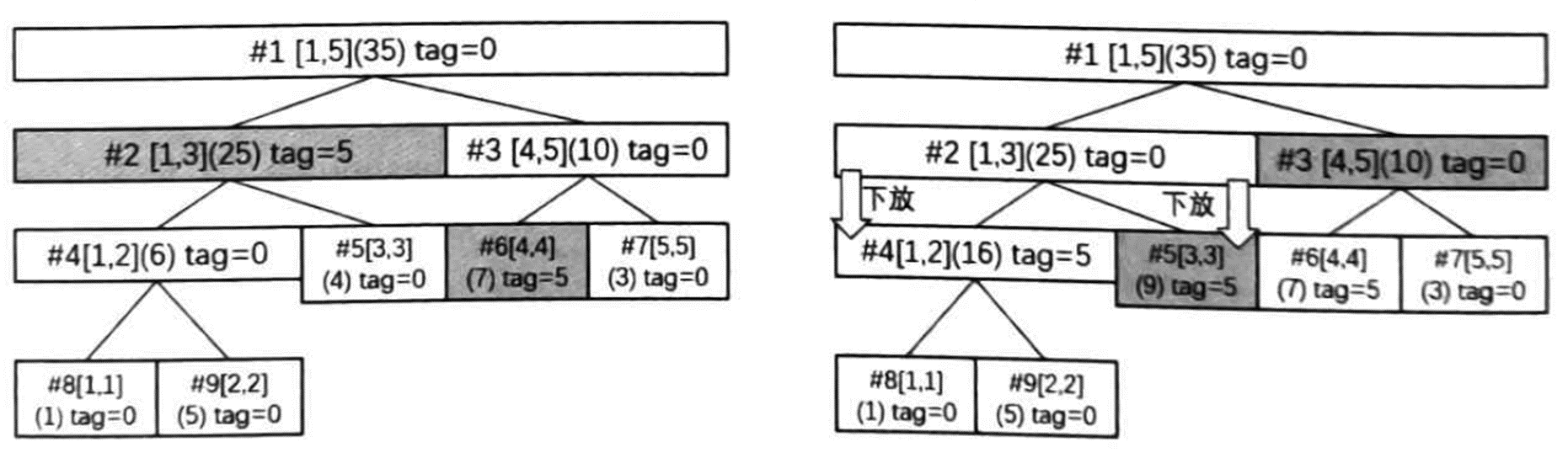
可以看到,对于打了延迟标记的结点,其维护的区间和是已经修改完成的信息,其子结点的值还没有被修改。也就是说,延迟标记起到的作用是记录子结点的每个数应该加上多少,而不是该结点本身的信息。代码如下,注意在查询时也要包含下放标记的过程:
void work(int cur, LL delta) {
int len = tree[cur].r - tree[cur].l + 1;
tree[cur].value += delta * len; // 修改当前结点的区间和
tree[cur].tag += delta; // 修改当前结点的延迟标记
}
void pushdown(int cur) {
if (tree[cur].tag != 0) {
work(LC, tree[cur].tag); // 下放标记给左子树
work(RC, tree[cur].tag); // 下放标记给右子树
tree[cur].tag = 0; // 因为标记信息已经传到下一层结点了,当前层清空标记
}
}
void update(int cur, int l, int r, LL delta) {
if (tree[cur].l >= l && tree[cur].r <= r) {
work(cur, delta); // 完全包含则直接打标记即可
return;
}
pushdown(cur); // 注意必须先将当前结点的标记下传,才能递归修改下面的结点
int mid = (tree[cur].l + tree[cur].r) / 2;
if (mid >= l) update(LC, l, r, delta);
if (mid < r) update(RC, l, r, delta);
pushup(cur);
}
LL query(int cur, int l, int r) { // 区间查询
if (tree[cur].l >= l && tree[cur].r <= r) { // 如果完全包含则直接返回区间和
return tree[cur].value;
}
pushdown(cur); // 查询的时候也需要将结点标记下传
int mid = (tree[cur].l + tree[cur].r) / 2;
LL res = 0;
// 若与左/右子结点区间有相交,则需递归处理
if (mid >= l) res += query(LC, l, r);
if (mid < r) res += query(RC, l, r);
return res;
}
上面的代码中,pushdown 函数是将延迟标记下传的过程,work 函数是更新结点信息的过程。成员变量 tag 记录的是当前结点应该加的值的大小,那么该区间的区间和需要增加的值就是长度乘上增加量。需要注意的是,在将标记下传后,应该清空当前结点的延迟标记。并且必须要先判断区间之间的完全包含关系,这样就会保证叶结点不会再 pushdown,否则一旦在叶结点 pushdown,可能会造成数组越界。
本题的完整代码如下:
#include <cstdio>
#define LC (cur*2)
#define RC (cur*2+1)
typedef long long LL;
const int MAXN = 100005;
struct Node {
int l, r; // 某个结点所代表的区间
LL value, tag; // value存储结点对应的区间和
// tag是区间加的延迟标记
};
LL a[MAXN];
Node tree[MAXN*4];
void pushup(int cur) {
// 2*cur是左子结点,2*cur+1是右子结点
tree[cur].value = tree[LC].value + tree[RC].value;
}
void build(int cur, int l, int r) {
tree[cur].l = l; tree[cur].r = r;
if (l == r) { // 到达叶子结点
tree[cur].value = a[l];
return;
}
int mid = (l + r) / 2; // 将区间分成[l,mid]和[mid+1,r]
build(LC, l, mid); build(RC, mid+1, r); // 递归构建子树
pushup(cur); // 由子区间的区间和更新当前区间的和
}
void work(int cur, LL delta) {
int len = tree[cur].r - tree[cur].l + 1;
tree[cur].value += delta * len; // 修改当前结点的区间和
tree[cur].tag += delta; // 修改当前结点的延迟标记
}
void pushdown(int cur) {
if (tree[cur].tag != 0) {
work(LC, tree[cur].tag); // 下放标记给左子树
work(RC, tree[cur].tag); // 下放标记给右子树
tree[cur].tag = 0; // 因为标记信息已经传到下一层结点了,当前层清空标记
}
}
void update(int cur, int l, int r, LL delta) {
if (tree[cur].l >= l && tree[cur].r <= r) {
work(cur, delta); // 完全包含则直接打标记即可
return;
}
pushdown(cur); // 注意必须先将当前结点的标记下传,才能递归修改下面的结点
int mid = (tree[cur].l + tree[cur].r) / 2;
if (mid >= l) update(LC, l, r, delta);
if (mid < r) update(RC, l, r, delta);
pushup(cur);
}
LL query(int cur, int l, int r) { // 区间查询
if (tree[cur].l >= l && tree[cur].r <= r) { // 如果完全包含则直接返回区间和
return tree[cur].value;
}
pushdown(cur); // 查询的时候也需要将结点标记下传
int mid = (tree[cur].l + tree[cur].r) / 2;
LL res = 0;
// 若与左/右子结点区间有相交,则需递归处理
if (mid >= l) res += query(LC, l, r);
if (mid < r) res += query(RC, l, r);
return res;
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
build(1, 1, n);
while (m--) {
int op; scanf("%d", &op);
if (op == 1) {
int x, y; LL k; scanf("%d%d%lld", &x, &y, &k); update(1, x, y, k);
} else {
int x, y; scanf("%d%d", &x, &y); printf("%lld\n", query(1, x, y));
}
}
return 0;
}
习题:P2357 守墓人
参考代码
#include <cstdio>
using ll = long long;
const int N = 2e5 + 5;
int n, f;
ll a[N]; // 存储初始风水值
// 线段树节点结构
struct Node {
ll sum; // 区间和
ll lazy; // 懒惰标记,表示区间内每个元素待增加的值
};
Node tr[N * 4]; // 线段树数组,大小开 4 倍以防越界
// pushup: 用子节点信息更新父节点
void pushup(int p) {
tr[p].sum = tr[p * 2].sum + tr[p * 2 + 1].sum;
}
// pushdown: 将父节点的懒惰标记下推给子节点
// p: 当前节点编号, l, r: 当前节点表示的区间
void pushdown(int p, int l, int r) {
if (tr[p].lazy != 0) {
int mid = l + (r - l) / 2;
// 更新左子节点的 sum 和 lazy
tr[p * 2].sum += tr[p].lazy * (mid - l + 1);
tr[p * 2].lazy += tr[p].lazy;
// 更新右子节点的 sum 和 lazy
tr[p * 2 + 1].sum += tr[p].lazy * (r - mid);
tr[p * 2 + 1].lazy += tr[p].lazy;
// 清除父节点的 lazy 标记
tr[p].lazy = 0;
}
}
// build: 构建线段树
// p: 当前节点编号, l, r: 当前节点表示的区间
void build(int p, int l, int r) {
tr[p].lazy = 0;
if (l == r) {
tr[p].sum = a[l];
return;
}
int mid = l + (r - l) / 2;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
pushup(p);
}
// update: 区间更新,给 [ul, ur] 区间每个数加上 k
// p: 当前节点, [l, r]: 当前节点区间, [ul, ur]: 更新区间
void update(int p, int l, int r, int ul, int ur, ll k) {
// 如果当前区间被更新区间完全覆盖
if (ul <= l && r <= ur) {
tr[p].sum += k * (r - l + 1);
tr[p].lazy += k;
return;
}
// 下推懒惰标记,准备更新子节点
pushdown(p, l, r);
int mid = l + (r - l) / 2;
if (ul <= mid) update(p * 2, l, mid, ul, ur, k);
if (ur > mid) update(p * 2 + 1, mid + 1, r, ul, ur, k);
// 子节点更新后,回溯更新父节点
pushup(p);
}
// query: 区间查询,查询 [ql, qr] 区间的和
// p: 当前节点, [l, r]: 当前节点区间, [ql, qr]: 查询区间
ll query(int p, int l, int r, int ql, int qr) {
// 如果当前区间被查询区间完全覆盖
if (ql <= l && r <= qr) return tr[p].sum;
// 下推懒惰标记,保证子节点信息正确
pushdown(p, l, r);
int mid = l + (r - l) / 2;
ll res = 0;
if (ql <= mid) res += query(p * 2, l, mid, ql, qr);
if (qr > mid) res += query(p * 2 + 1, mid + 1, r, ql, qr);
return res;
}
int main()
{
scanf("%d%d", &n, &f);
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
build(1, 1, n); // 初始化线段树
for (int i = 0; i < f; i++) {
int op; scanf("%d", &op);
if (op == 1) { // 区间 [l, r] 加 k
int l, r; ll k;
scanf("%d%d%lld", &l, &r, &k);
update(1, 1, n, l, r, k);
} else if (op == 2) { // 主墓碑加 k (等价于区间 [1, 1] 加 k)
ll k; scanf("%lld", &k);
update(1, 1, n, 1, 1, k);
} else if (op == 3) { // 主墓碑减 k (等价于区间 [1, 1] 加 -k)
ll k; scanf("%lld", &k);
update(1, 1, n, 1, 1, -k);
} else if (op == 4) { // 查询区间 [l, r] 的和
int l, r; scanf("%d%d", &l, &r);
printf("%lld\n", query(1, 1, n, l, r));
} else { // 查询主墓碑的值 (等价于查询区间 [1, 1] 的和)
printf("%lld\n", query(1, 1, n, 1, 1));
}
}
return 0;
}
线段树的应用
例题:P3870 [TJOI2009] 开关
给定一个初始为 \(0\) 的长度为 \(n\) 的数列,进行 \(m\) 次操作,要求支持两种操作:
1.给区间 \([a,b]\) 的所有数字对 \(1\) 取异或。
2.求区间 \([a,b]\) 内 \(1\) 的个数。
数据范围:\(1 \le n,m \le 10^5\)
分析:不难发现,要求的“区间内 \(1\) 的个数”这一问题具有可合并性,并且“区间异或”这一操作很容易通过线段树的延迟标记实现,定义延迟标记的含义为区间内所有数字都异或上该值,修改时,将延迟标记也异或上 \(1\)。在每次异或 \(1\) 时,原有的 \(1\) 会变成 \(0\),原有的 \(0\) 会变成 \(1\),也即区间内 \(1\) 的个数会变成区间长度减去原来的个数。
#include <cstdio>
#define LC (2 * cur)
#define RC (2 * cur + 1)
const int N = 1e5 + 5;
struct Node {
int l, r, cnt, tag;
};
Node tree[N * 4];
void pushup(int cur) {
tree[cur].cnt = tree[LC].cnt + tree[RC].cnt;
}
void build(int cur, int l, int r) {
tree[cur].l = l; tree[cur].r = r;
if (l == r) return;
int mid = (l + r) / 2;
build(LC, l, mid); build(RC, mid + 1, r);
}
void work(int cur) {
tree[cur].cnt = tree[cur].r - tree[cur].l + 1 - tree[cur].cnt;
tree[cur].tag ^= 1;
}
void pushdown(int cur) {
if (tree[cur].tag) {
work(LC); work(RC);
}
tree[cur].tag = 0;
}
void update(int cur, int l, int r) {
if (tree[cur].l >= l && tree[cur].r <= r) {
work(cur); return;
}
pushdown(cur);
int mid = (tree[cur].l + tree[cur].r) / 2;
if (mid >= l) update(LC, l, r);
if (mid + 1 <= r) update(RC, l, r);
pushup(cur);
}
int query(int cur, int l, int r) {
if (tree[cur].l >= l && tree[cur].r <= r) return tree[cur].cnt;
pushdown(cur);
int mid = (tree[cur].l + tree[cur].r) / 2;
int res = 0;
if (mid >= l) res += query(LC, l, r);
if (mid + 1 <= r) res += query(RC, l, r);
return res;
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
build(1, 1, n);
while (m--) {
int c, a, b; scanf("%d%d%d", &c, &a, &b);
if (c == 0) update(1, a, b);
else printf("%d\n", query(1, a, b));
}
return 0;
}
例题:P1438 无聊的数列
维护一个长度为 \(n\) 的数列 \(a\)。要求支持 \(m\) 此操作,操作有两种类型:
1.1 l r k d:给出一个长度等于 \(r-l+1\) 的等差数列,首项为 \(k\),公差为 \(d\),并将它对应加到 \([l,r]\) 范围中的每一个数上。即:令 \(a_l = a_l + k, a_{l+1} = a_{l+1} + k + d, \dots, a_r = a_r + k + (r-l) \times d\)。
2.2 p:询问序列的第 \(p\) 个数的值 \(a_p\)。
数据范围:\(n,m \le 10^5\)
分析:这是一个区间加等差数列的问题。考虑等差数列有两个要素:首项 \(k\) 和公差 \(d\)。只要这两项确定了,等差数列就唯一确定了。而这两个要素具有“可加性”:将首项分别为 \(k_1, k_2\),公差分别为 \(d_1,d_2\) 的两个等差数列的每一项对应相加,得到的数列也是一个等差数列,且它的首项为 \(k_1+k_2\),公差为 \(d_1+d_2\)。
例如,将数列 \(1,2,3\)(首项为 \(1\),公差为 \(1\))和 \(1,3,5\)(首项为 \(1\),公差为 \(2\))对应相加,得到数列 \(2,5,8\)。它的首项为 \(1+1=2\),公差为 \(1+2=3\)。
于是使用两个延迟标记,分别表示首项和公差即可。
#include <cstdio>
#define LC (2 * cur)
#define RC (2 * cur + 1)
typedef long long LL;
const int N = 1e5 + 5;
int a[N];
struct Node {
int l, r;
LL val, k, d;
};
Node tree[N * 4];
void build(int cur, int l, int r) {
tree[cur].l = l; tree[cur].r = r;
if (l == r) {
tree[cur].val = a[l]; return;
}
int mid = (l + r) / 2;
build(LC, l, mid); build(RC, mid + 1, r);
}
void work(int cur, LL k, LL d) {
tree[cur].k += k; tree[cur].d += d;
tree[cur].val += k;
}
void pushdown(int cur) {
if (tree[cur].k != 0 || tree[cur].d != 0) {
int mid = (tree[cur].l + tree[cur].r) / 2;
work(LC, tree[cur].k, tree[cur].d);
work(RC, tree[cur].k + (mid + 1 - tree[cur].l) * tree[cur].d, tree[cur].d);
tree[cur].k = tree[cur].d = 0;
}
}
void update(int cur, int l, int r, LL k, LL d) {
if (tree[cur].l >= l && tree[cur].r <= r) {
work(cur, k + d * (tree[cur].l - l), d); return;
}
pushdown(cur);
int mid = (tree[cur].l + tree[cur].r) / 2;
if (mid >= l) update(LC, l, r, k, d);
if (mid + 1 <= r) update(RC, l, r, k, d);
}
LL query(int cur, int p) {
if (tree[cur].l == tree[cur].r) return tree[cur].val;
pushdown(cur);
int mid = (tree[cur].l + tree[cur].r) / 2;
if (p <= mid) return query(LC, p);
else return query(RC, p);
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
build(1, 1, n);
while (m--) {
int opt; scanf("%d", &opt);
if (opt == 1) {
int l, r, k, d; scanf("%d%d%d%d", &l, &r, &k, &d);
update(1, l, r, k, d);
} else {
int p; scanf("%d", &p);
printf("%lld\n", query(1, p));
}
}
return 0;
}
例题:P1253 扶苏的问题
给定一个长度为 \(n\) 的序列 \(a\),要求支持 \(q\) 次操作,共有三种类型的操作:
1.给定区间 \([l,r]\),将区间内每个数都修改为 \(x\);
2.给定区间 \([l,r]\),将区间内每个数都加上 \(x\);
3.给定区间 \([l,r]\),求区间内的最大值。
数据范围:\(1 \le n,q \le 10^6; -10^9 \le a_i,x \le 10^9\)。
分析:本题中所求的“区间最大值”也可以使用线段树维护:父结点的区间最大值就是它两个子结点的区间最大值中较大的一个。
对于修改操作,可以使用两个延迟标记,一个表示区间赋值为 \(x\)(记为 \(cover\)),一个表示区间加上 \(x\)(记为 \(add\))。当对一个结点执行操作 \(1\) 时,直接将 \(cover\) 赋值为 \(x\),\(add\) 清空;执行操作 \(2\) 时,若 \(cover\) 存在,则将 \(cover\) 加上 \(x\),否则将 \(add\) 加上 \(x\)。
需要注意的是,因为操作时可能赋值为 \(0\) 或负数,所以需要用一个在计算过程中永远不可能出现的数(例如 \(10^{16}\))来表示覆盖标记不存在。
#include <cstdio>
#include <algorithm>
#define LC (cur*2)
#define RC (cur*2+1)
using namespace std;
typedef long long LL;
const int MAXN = 1000005;
const LL INF = 1e16;
struct Node {
int l, r;
// value为区间最大值,add为区间加法标记,cover为区间赋值标记
LL value, add, cover;
};
LL a[MAXN];
Node tree[MAXN*4];
void pushup(int cur) {
tree[cur].value = max(tree[LC].value, tree[RC].value);
}
void build(int cur, int l, int r) {
tree[cur].l = l;
tree[cur].r = r;
tree[cur].cover = INF; // 注意cover标记的初始化
if (l == r) {
tree[cur].value = a[l];
return;
}
int mid = (l + r) / 2;
build(LC, l, mid);
build(RC, mid+1, r);
pushup(cur);
}
void work(int cur, LL x, int op) { // op表示操作类型
if (op == 1) { // 区间赋值
tree[cur].value = tree[cur].cover = x;
tree[cur].add = 0;
} else { // 区间加法
tree[cur].value += x;
if (tree[cur].cover != INF) tree[cur].cover += x;
else tree[cur].add += x;
}
}
void pushdown(int cur) {
if (tree[cur].cover != INF) {
work(LC, tree[cur].cover, 1); work(RC, tree[cur].cover, 1);
tree[cur].cover = INF; // 清空cover标记
}
if (tree[cur].add != 0) {
work(LC, tree[cur].add, 2); work(RC, tree[cur].add, 2);
tree[cur].add = 0; // 清空add标记
}
}
void update(int cur, int l, int r, LL delta, int op) {
if (tree[cur].l >= l && tree[cur].r <= r) {
work(cur, delta, op);
return;
}
pushdown(cur);
int mid = (tree[cur].l + tree[cur].r) / 2;
if (mid >= l) update(LC, l, r, delta, op);
if (mid < r) update(RC, l, r, delta, op);
pushup(cur);
}
LL query(int cur, int l, int r) { // 区间查询
// 全包含
if (tree[cur].l >= l && tree[cur].r <= r) {
return tree[cur].value;
}
pushdown(cur);
LL res = -INF;
int mid = (tree[cur].l + tree[cur].r) / 2;
if (mid >= l) res = max(res, query(LC, l, r));
if (mid < r) res = max(res, query(RC, l, r));
return res;
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
build(1, 1, n);
while (m--) {
int op;
scanf("%d", &op);
if (op < 3) {
int x, y;
LL k;
scanf("%d%d%lld", &x, &y, &k);
update(1, x, y, k, op);
} else {
int x, y;
scanf("%d%d", &x, &y);
printf("%lld\n", query(1, x, y));
}
}
return 0;
}
例题:P3373【模板】线段树 2
给定一个长度为 \(n (1 \le n \le 10^5)\) 的数列,需要进行下面三种操作:
1.将区间内每个数乘上 \(x\);
2.将区间内每个数加上 \(x\);
3.求数列的区间和,答案对一个大数取模。
分析:这是一个多标记线段树的题。本题中一共出现了两种修改,分别为加法和乘法,考虑用两个标记分别维护它们。
设 \(add\) 表示某个区间的加法标记,\(mul\) 表示某个区间的乘法标记。这里 \(mul\) 表示的是原区间和乘上的数,\(add\) 表示的是区间和加上的数,设原区间和为 \(s\),则最终计算的区间和为 \(s \times mul + add\),否则难以维护。值得注意的是,进行区间加操作时,对前面的区间乘操作没有影响,而进行区间乘操作时,相当于将之前区间要加的数也乘上了 \(x\)。也即:若设原区间和为 \(s\),新加了 \(a\),现在要乘上 \(b\),则新的区间和是 \((s+a) \times b\),也即 \(s \times b + a \times b\)。
因此,标记的下传顺序十分关键:在 pushdown 时,必须先下传乘法标记,再下传加法标记。因为乘法标记在下传时,需要让子结点的加法标记也乘上当前结点的乘法标记值,如果先下传加法标记,会让下传的那部分加法标记再乘上乘法标记,而事实上这部分标记已经在原结点乘过了,因此会计算错误。
参考代码
#include <cstdio>
#define LC (cur*2)
#define RC (cur*2+1)
typedef long long LL;
const int MAXN = 500005;
struct Node {
int l, r;
LL value, add, mul;
};
LL a[MAXN], m;
Node tree[MAXN*4];
void pushup(int cur) {
tree[cur].value = (tree[LC].value + tree[RC].value) % m;
}
void build(int cur, int l, int r) {
tree[cur].l = l;
tree[cur].r = r;
tree[cur].mul = 1;
if (l == r) {
tree[cur].value = a[l] % m;
return;
}
int mid = (l + r) / 2;
build(LC, l, mid);
build(RC, mid+1, r);
pushup(cur);
}
void work(int cur, LL x, int op) { //对cur这个节点进行具体的更新操作
if (op == 1) {
tree[cur].value *= x; tree[cur].value %= m;
tree[cur].mul *= x; tree[cur].mul %= m;
tree[cur].add *= x; tree[cur].add %= m;
} else {
tree[cur].value += x * (tree[cur].r-tree[cur].l+1) % m;
tree[cur].value %= m;
tree[cur].add += x; tree[cur].add %= m;
}
}
void pushdown(int cur) {
if (tree[cur].mul != 1) {
work(LC, tree[cur].mul, 1); work(RC, tree[cur].mul, 1);
tree[cur].mul = 1;
}
if (tree[cur].add != 0) {
work(LC, tree[cur].add, 2); work(RC, tree[cur].add, 2);
tree[cur].add = 0;
}
}
void update(int cur, int l, int r, LL x, int op) {
if (tree[cur].l >= l && tree[cur].r <= r) {
work(cur, x, op);
return;
}
pushdown(cur);
int mid = (tree[cur].l + tree[cur].r) / 2;
if (mid >= l) update(LC, l, r, x, op);
if (mid < r) update(RC, l, r, x, op);
pushup(cur);
}
LL query(int cur, int l, int r) { // 区间查询
if (tree[cur].l >= l && tree[cur].r <= r) { // 完全包含
return tree[cur].value;
}
pushdown(cur);
int mid = (tree[cur].l + tree[cur].r) / 2;
LL res = 0;
if (mid >= l) {
res += query(LC, l, r); res %= m;
}
if (mid < r) {
res += query(RC, l, r); res %= m;
}
return res;
}
int main() {
int n, q;
scanf("%d%d%lld", &n, &q, &m);
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
build(1, 1, n);
while (q--) {
int op;
scanf("%d", &op);
if (op < 3) {
int x, y;
LL k;
scanf("%d%d%lld", &x, &y, &k);
update(1, x, y, k, op);
} else {
int x, y;
scanf("%d%d", &x, &y);
printf("%lld\n", query(1, x, y));
}
}
return 0;
}
习题:P4588 [TJOI2018] 数学计算
解题思路
本题的核心是维护一个动态的乘积,并随时查询它对 \(M\) 取模的结果。
一个直接的想法是维护 \(x\) 的值,每次操作都进行乘法或除法。但由于 \(Q\) 和 \(m\) 都很大,\(x\) 的值会迅速超出 long long 的表示范围,因此不能直接存储 \(x\)。
所有计算都必须在模 \(M\) 的意义下进行,模意义下的乘法很简单,但除法 \(x / d\) 等价于乘以 \(d\) 的乘法逆元 \(d^{-1}\),计算乘法逆元需要 \(d\) 和模数 \(M\) 互质。然而,题目没有保证 \(M\) 是质数,也没有保证乘数 \(m\) 与 \(M\) 互质,所以求逆元的方法不通用。
需要转换思路,在任意时刻,\(x\) 的值等于所有“未被撤销”的类型 1 操作的乘数 \(m\) 的总乘积。
1 m操作:为总乘积引入一个新的因子 \(m\)。2 pos操作:从总乘积中移除第 \(\text{pos}\) 次操作引入的因子。
问题就转化为了:维护一个动态的数字序列,初始值全是 1,需要支持单点修改操作(乘就是把 1 改成 \(m\),除就是改回 1),并快速查询所有元素的乘积模 \(M\) 的值。
参考代码
#include <cstdio>
using ll = long long;
const int Q = 100005;
ll M; // 模数
ll tr[Q * 4]; // 线段树数组
// pushup 操作,用子节点的值更新父节点
// 父节点的值是左右子节点值的乘积模 M
void pushup(int p) {
tr[p] = (tr[p * 2] * tr[p * 2 + 1]) % M;
}
// build 操作,构建线段树
// p: 当前节点索引, l, r: 当前节点代表的区间 [l, r]
// 初始化所有叶子节点为 1,因为初始总乘积为 1
void build(int p, int l, int r) {
if (l == r) {
tr[p] = 1;
return;
}
int mid = l + (r - l) / 2;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
pushup(p);
}
// update 操作,单点更新
// p: 当前节点索引, l, r: 当前节点代表的区间 [l, r]
// pos: 要更新的位置, val: 新的值
void update(int p, int l, int r, int pos, ll val) {
if (l == r) {
tr[p] = val;
return;
}
int mid = l + (r - l) / 2;
if (pos <= mid) {
update(p * 2, l, mid, pos, val);
} else {
update(p * 2 + 1, mid + 1, r, pos, val);
}
pushup(p);
}
// 解决单个测试用例的函数
void solve() {
int q;
scanf("%d%lld", &q, &M);
// 为每个测试用例构建一个新的线段树
// 树的区间是 [1, Q],代表 Q 次操作
build(1, 1, q);
for (int i = 1; i <= q; ++i) {
int type;
ll val;
scanf("%d%lld", &type, &val);
if (type == 1) {
// 操作 1: x = x * m
// 在线段树的第 i 个位置更新乘数 m
update(1, 1, q, i, val);
} else {
// 操作 2: x = x / (第 pos 次操作的乘数)
// 将第 pos 次操作的贡献从乘积中移除,即将其在线段树中的值变为 1
int pos = val;
update(1, 1, q, pos, 1);
}
// 根节点 tr[1] 存储了当前所有有效乘数的总乘积模 M
printf("%lld\n", tr[1] % M);
}
}
int main() {
int t; scanf("%d", &t);
while (t--) {
solve();
}
return 0;
}
习题:P1558 色板游戏
解题思路
本题要求对一个序列进行两种操作:区间赋值(染色)和区间查询(统计不同颜色数量)。
题目中一个非常重要的约束是颜色的总数 \(T\) 非常小(\(T \le 30\)),这个特点是解决本题的关键。
当需要处理“集合”类的状态,且集合内元素种类不多时,可以考虑使用状态压缩的技巧。由于 \(T \le 30\),可以用一个 32 位的整数的二进制位来表示一个颜色集合。例如,整数的第 \(i-1\) 位为 1,表示颜色 \(i\) 存在;为 0 则表示不存在。这样,一个整数就可以代表任意一个颜色集合。
结合区间操作的需求,带懒惰标记的线段树成为理想的选择。
参考代码
#include <iostream>
using namespace std;
const int MAX_L = 100005;
int L, T, O;
// 线段树节点结构
struct Node {
int mask; // 用一个 bitmask 表示区间内的颜色集合
int lazy; // 懒惰标记,lazy > 0 表示整个区间被涂成颜色 lazy
};
Node tr[MAX_L * 4]; // 线段树数组
// pushup: 用子节点信息更新父节点
// 父节点的颜色集合是子节点颜色集合的并集
void pushup(int p) {
tr[p].mask = tr[p * 2].mask | tr[p * 2 + 1].mask;
}
// pushdown: 将父节点的懒惰标记下推给子节点
void pushdown(int p) {
// 如果存在懒惰标记
if (tr[p].lazy > 0) {
int color = tr[p].lazy;
// 更新左子节点
tr[p * 2].lazy = color;
tr[p * 2].mask = (1 << (color - 1));
// 更新右子节点
tr[p * 2 + 1].lazy = color;
tr[p * 2 + 1].mask = (1 << (color - 1));
// 清除父节点的懒惰标记
tr[p].lazy = 0;
}
}
// build: 构建线段树
// p: 当前节点索引, l, r: 当前节点代表的区间 [l, r]
void build(int p, int l, int r) {
tr[p].lazy = 0;
if (l == r) {
// 初始时,所有方格都是 1 号色
tr[p].mask = (1 << (1 - 1));
return;
}
int mid = l + (r - l) / 2;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
pushup(p);
}
// update: 区间更新,将 [ul, ur] 区间涂成 color
// p: 当前节点, [l, r]: 当前节点区间, [ul, ur]: 更新区间
void update(int p, int l, int r, int ul, int ur, int color) {
// 如果当前区间被更新区间完全覆盖
if (ul <= l && r <= ur) {
tr[p].lazy = color;
tr[p].mask = (1 << (color - 1));
return;
}
// 下推懒惰标记,准备更新子节点
pushdown(p);
int mid = l + (r - l) / 2;
if (ul <= mid) {
update(p * 2, l, mid, ul, ur, color);
}
if (ur > mid) {
update(p * 2 + 1, mid + 1, r, ul, ur, color);
}
// 子节点更新后,回溯更新父节点
pushup(p);
}
// query: 区间查询,查询 [ql, qr] 区间的颜色集合
// p: 当前节点, [l, r]: 当前节点区间, [ql, qr]: 查询区间
int query(int p, int l, int r, int ql, int qr) {
// 如果当前区间被查询区间完全覆盖
if (ql <= l && r <= qr) {
return tr[p].mask;
}
// 下推懒惰标记,保证子节点信息正确
pushdown(p);
int mid = l + (r - l) / 2;
int res_mask = 0;
if (ql <= mid) {
res_mask |= query(p * 2, l, mid, ql, qr);
}
if (qr > mid) {
res_mask |= query(p * 2 + 1, mid + 1, r, ql, qr);
}
return res_mask;
}
int main() {
cin >> L >> T >> O;
// 初始化线段树
build(1, 1, L);
for (int i = 0; i < O; ++i) {
char op;
cin >> op;
if (op == 'C') {
int a, b, c;
cin >> a >> b >> c;
if (a > b) swap(a, b);
update(1, 1, L, a, b, c);
} else { // op == 'P'
int a, b;
cin >> a >> b;
if (a > b) swap(a, b);
int mask = query(1, 1, L, a, b);
// 使用 __builtin_popcount 高效统计 bitmask 中 1 的数量
cout << __builtin_popcount(mask) << "\n";
}
}
return 0;
}
习题:CF558E A Simple Task
解题思路
使用计数排序的思想。对于每一个询问,查询每种字母的在区间内的个数,使用计数排序的方式来更新区间信息。
构建 \(26\) 棵线段树面向每一种字母。这样一来,结合计数排序的模式,问题就转化为了区间个数查询和区间个数更新,需要使用延迟标记技术来更新区间信息。
时间复杂度为 \(O(Aq \log n)\),其中 \(A\) 是符号的种类数,在这道题中相当于 \(26\)。
参考代码
#include <cstdio>
#define LC (2 * cur)
#define RC (2 * cur + 1)
const int N = 1e5 + 5;
char s[N], ans[N];
int cnt[26];
struct Node {
int l, r, cnt, cover;
};
Node tree[26][N * 4];
void pushup(int idx, int cur) {
tree[idx][cur].cnt = tree[idx][LC].cnt + tree[idx][RC].cnt;
}
void build(int idx, int cur, int l, int r) {
tree[idx][cur].l = l; tree[idx][cur].r = r; tree[idx][cur].cover = -1;
if (l == r) return;
int mid = (l + r) / 2;
build(idx, LC, l, mid);
build(idx, RC, mid + 1, r);
pushup(idx, cur);
}
void work(int idx, int cur, int val) {
tree[idx][cur].cover = val;
if (tree[idx][cur].cover == 1)
tree[idx][cur].cnt = tree[idx][cur].r - tree[idx][cur].l + 1;
else
tree[idx][cur].cnt = 0;
}
void pushdown(int idx, int cur) {
if (tree[idx][cur].cover != -1) {
work(idx, LC, tree[idx][cur].cover);
work(idx, RC, tree[idx][cur].cover);
tree[idx][cur].cover = -1;
}
}
void update(int idx, int cur, int l, int r, int val) {
if (tree[idx][cur].l >= l && tree[idx][cur].r <= r) {
work(idx, cur, val);
return;
}
pushdown(idx, cur);
int mid = (tree[idx][cur].l + tree[idx][cur].r) / 2;
if (mid >= l) update(idx, LC, l, r, val);
if (mid + 1 <= r) update(idx, RC, l, r, val);
pushup(idx, cur);
}
int query(int idx, int cur, int l, int r) {
if (tree[idx][cur].l >= l && tree[idx][cur].r <= r)
return tree[idx][cur].cnt;
pushdown(idx, cur);
int mid = (tree[idx][cur].l + tree[idx][cur].r) / 2;
int res = 0;
if (mid >= l) res += query(idx, LC, l, r);
if (mid + 1 <= r) res += query(idx, RC, l, r);
return res;
}
int main()
{
int n, q; scanf("%d%d%s", &n, &q, s + 1);
for (int i = 0; i < 26; i++) build(i, 1, 1, n);
for (int i = 1; i <= n; i++) {
update(s[i] - 'a', 1, i, i, 1);
}
while (q--) {
int l, r, k; scanf("%d%d%d", &l, &r, &k);
for (int i = 0; i < 26; i++) {
cnt[i] = query(i, 1, l, r);
update(i, 1, l, r, 0);
}
int cur = k == 1 ? l : r;
for (int i = 0; i < 26; i++) {
if (cnt[i] == 0) continue;
if (k == 1) {
update(i, 1, cur, cur + cnt[i] - 1, 1);
cur += cnt[i];
} else {
update(i, 1, cur - cnt[i] + 1, cur, 1);
cur -= cnt[i];
}
}
}
for (int i = 0; i < 26; i++) {
for (int j = 1; j <= n; j++)
if (query(i, 1, j, j) == 1) ans[j] = 'a' + i;
}
for (int i = 1; i <= n; i++) printf("%c", ans[i]);
printf("\n");
return 0;
}
习题:P4145 上帝造题的七分钟 2 / 花神游历各国
解题思路
本题要求对一个序列进行区间更新和区间查询,这是一个典型的线段树问题。
- 查询操作:查询区间和,这是线段树最基础的功能。
- 更新操作:将区间内的每个数都进行开方操作,这个操作与常见的区间加、减、区间赋值不同,它没有一个简单的分配律可以直接用传统的懒惰标记来处理,无法通过一个父节点的懒惰标记直接计算出子节点的懒惰标记。
既然传统的懒惰标记行不通,就需要深入分析“开平方”这个操作的性质,寻找优化的突破口。
关键性质:一个数在经过反复的开方取整后,其值会迅速减小。
- 例如,一个高达 \(10^{12}\) 的数,在经过少数几次(大约六七次)开方操作后,就会变为 1。
- 一旦一个数变为 1 或 0,再对它进行开方取整,其值将不再改变。(\(\lfloor\sqrt{1}\rfloor = 1\), \(\lfloor\sqrt{0}\rfloor = 0\))
这个性质是本题的核心,它意味着序列中的每个数被有效修改(即数值发生变化)的次数非常有限,可以利用这一点对线段树的更新操作进行剪枝优化。
例如,每个线段树节点除了维护区间和之外,再额外维护区间最大值。如果一个线段树的节点代表的区间最大值已经小于等于 1,那么这个区间内所有的数必然都已经是 0 或 1。此时再对这个区间进行开方操作,不会改变其中任何一个数的值,因此可以直接返回。
参考代码
#include <cstdio>
#include <cmath>
#include <algorithm>
using ll = long long;
using namespace std;
const int N = 100005;
int n, m;
ll a[N];
// 线段树节点结构
struct Node {
ll sum; // 区间和
ll max_val; // 区间最大值
};
Node tr[N * 4]; // 线段树数组
// pushup: 用子节点信息更新父节点
void pushup(int p) {
tr[p].sum = tr[p * 2].sum + tr[p * 2 + 1].sum;
tr[p].max_val = max(tr[p * 2].max_val, tr[p * 2 + 1].max_val);
}
// build: 构建线段树
void build(int p, int l, int r) {
if (l == r) {
tr[p].sum = a[l];
tr[p].max_val = a[l];
return;
}
int mid = l + (r - l) / 2;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
pushup(p);
}
// update: 区间开方更新
// p: 当前节点, [l, r]: 当前节点区间, [ul, ur]: 更新区间
void update(int p, int l, int r, int ul, int ur) {
// 剪枝优化:如果当前区间的最大值已经 <= 1,
// 开方操作不会改变任何值,因此无需继续递归。
if (tr[p].max_val <= 1) {
return;
}
// 到达叶子节点,执行开方操作
if (l == r) {
tr[p].sum = floor(sqrt(tr[p].sum));
tr[p].max_val = tr[p].sum;
return;
}
int mid = l + (r - l) / 2;
if (ul <= mid) {
update(p * 2, l, mid, ul, ur);
}
if (ur > mid) {
update(p * 2 + 1, mid + 1, r, ul, ur);
}
// 回溯时更新父节点信息
pushup(p);
}
// query: 区间求和
// p: 当前节点, [l, r]: 当前节点区间, [ql, qr]: 查询区间
ll query(int p, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) {
return tr[p].sum;
}
int mid = l + (r - l) / 2;
ll res = 0;
if (ql <= mid) {
res += query(p * 2, l, mid, ql, qr);
}
if (qr > mid) {
res += query(p * 2 + 1, mid + 1, r, ql, qr);
}
return res;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%lld", &a[i]);
}
build(1, 1, n);
scanf("%d", &m);
for (int i = 0; i < m; ++i) {
int k, l, r;
scanf("%d%d%d", &k, &l, &r);
if (l > r) swap(l, r);
if (k == 0) { // 区间开方
update(1, 1, n, l, r);
} else { // k == 1, 区间求和
printf("%lld\n", query(1, 1, n, l, r));
}
}
return 0;
}
习题:SP2713 GSS4 - Can you answer these queries IV
解题思路
参考代码
#include <cstdio>
#include <cmath>
#include <algorithm>
using ll = long long;
using namespace std;
const int N = 100005;
int n, m;
ll a[N];
// 线段树节点结构
struct Node {
ll sum; // 区间和
ll max_val; // 区间最大值
};
Node tr[N * 4]; // 线段树数组
// pushup: 用子节点信息更新父节点
void pushup(int p) {
tr[p].sum = tr[p * 2].sum + tr[p * 2 + 1].sum;
tr[p].max_val = max(tr[p * 2].max_val, tr[p * 2 + 1].max_val);
}
// build: 构建线段树
void build(int p, int l, int r) {
if (l == r) {
tr[p].sum = a[l];
tr[p].max_val = a[l];
return;
}
int mid = l + (r - l) / 2;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
pushup(p);
}
// update: 区间开方更新
// p: 当前节点, [l, r]: 当前节点区间, [ul, ur]: 更新区间
void update(int p, int l, int r, int ul, int ur) {
// 剪枝优化:如果当前区间的最大值已经 <= 1,
// 开方操作不会改变任何值,因此无需继续递归。
if (tr[p].max_val <= 1) {
return;
}
// 到达叶子节点,执行开方操作
if (l == r) {
tr[p].sum = floor(sqrt(tr[p].sum));
tr[p].max_val = tr[p].sum;
return;
}
int mid = l + (r - l) / 2;
if (ul <= mid) {
update(p * 2, l, mid, ul, ur);
}
if (ur > mid) {
update(p * 2 + 1, mid + 1, r, ul, ur);
}
// 回溯时更新父节点信息
pushup(p);
}
// query: 区间求和
// p: 当前节点, [l, r]: 当前节点区间, [ql, qr]: 查询区间
ll query(int p, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) {
return tr[p].sum;
}
int mid = l + (r - l) / 2;
ll res = 0;
if (ql <= mid) {
res += query(p * 2, l, mid, ql, qr);
}
if (qr > mid) {
res += query(p * 2 + 1, mid + 1, r, ql, qr);
}
return res;
}
int main() {
int case_count = 1;
while (scanf("%d", &n) != EOF) {
if (case_count > 1) {
printf("\n");
}
printf("Case #%d:\n", case_count++);
for (int i = 1; i <= n; ++i) {
scanf("%lld", &a[i]);
}
build(1, 1, n);
scanf("%d", &m);
for (int i = 0; i < m; ++i) {
int k, l, r;
scanf("%d%d%d", &k, &l, &r);
if (l > r) swap(l, r);
if (k == 0) { // 区间开方
update(1, 1, n, l, r);
} else { // k == 1, 区间求和
printf("%lld\n", query(1, 1, n, l, r));
}
}
}
return 0;
}
习题:P1937 [USACO10MAR] Barn Allocation G
解题思路
问题的关键在于决定以何种顺序来处理奶牛的请求,一个非常有效且经典的贪心策略是按区间的结束点排序。具体来说,应该优先考虑那些结束畜栏编号更小的请求。
为什么这个策略是优的?直观上讲,一个早早结束的请求会更快地“释放”它所占用的资源(畜栏容量),从而为后续更多的请求提供可能性。优先满足一个早结束的请求,对后续决策的影响更小,留下的选择空间更大,这与 P1803 凌乱的yyy / 线段覆盖 的经典贪心思路是一致的。
将所有 \(M\) 个请求按照其结束点从小到大进行排序,按排序后的顺序,依次遍历每个请求。对于当前请求,检查它是否能够被满足。满足的条件是:该请求区间 \([A,B]\) 内的所有畜栏都必须至少有 \(1\) 个空位。换句话说,需要查询区间 \([A,B]\) 内畜栏容量的最小值,如果这个最小值大于 \(0\),则请求可以被满足。如果可以满足,将满足的请求总数加一,并将区间 \([A,B]\) 内所有畜栏的容量都减 \(1\),因为被这头牛占用了。如果不可以满足,直接跳过,考虑下一个请求。遍历完所有请求,累计的满足数量就是最终答案。
在上述算法中,需要高效地执行两个核心操作:
- 区间最小值查询:查询 \([A,B]\) 范围内的最小畜栏容量。
- 区间更新:将 \([A,B]\) 范围内的所有畜栏容量减 \(1\)。
能够同时高效处理“区间查询”和“区间更新”的数据结构是线段树,并且需要配合懒惰标记来优化区间更新的效率。线段树基于初始的 \(N\) 个畜栏的容量数组来构建,每个节点存储其对应区间的最小值。每个节点有一个 \(tag\),记录该区间被“整体减少”了多少。当更新一个大区间时,只修改对应节点的 \(tag\),而不是递归到底,\(tag\) 会在后续查询或更新需要深入到子节点时再向下传递。
对请求排序的时间复杂度为 \(O(M \log M)\),构建线段树的复杂度为 \(O(N)\)。处理 \(M\) 个请求,每个请求包含一次查询 \(O(\log N)\) 和一次更新 \(O(\log N)\),这部分的复杂度为 \(O(M \log N)\)。
总复杂度为 \(O(N + M \log M + M \log N)\)。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 100005;
const int INF = 1e9;
// c: 存储每个畜栏的初始容量
// bg, ed, mid: 线段树节点对应的区间起点、终点、中点
// val: 线段树节点存储的区间最小值
// tag: 懒惰标记,记录区间被减去的总值
int c[N], bg[N * 4], ed[N * 4], mid[N * 4], val[N * 4], tag[N * 4];
// 定义请求结构体,包含起始和结束畜栏编号
struct Request {
int a, b;
};
Request r[N];
// --- 线段树操作 ---
// 从子节点更新父节点的最小值
void pushup(int u) {
val[u] = min(val[u * 2], val[u * 2 + 1]);
}
// 构建线段树
void build(int u, int l, int r) {
bg[u] = l; ed[u] = r; mid[u] = (l + r) / 2;
tag[u] = 0; // 初始化懒惰标记
if (l == r) { // 到达叶子节点
val[u] = c[l];
return;
}
// 递归构建左右子树
build(u * 2, l, mid[u]);
build(u * 2 + 1, mid[u] + 1, r);
pushup(u); // 回溯时更新父节点
}
// 对节点 u 应用更新操作(值减 d,标记加 d)
void work(int u, int d) {
val[u] -= d;
tag[u] += d;
}
// 向下传递懒惰标记
void pushdown(int u) {
if (tag[u] != 0) {
// 将父节点的标记传递给左右子节点
work(u * 2, tag[u]);
work(u * 2 + 1, tag[u]);
// 清除父节点的标记
tag[u] = 0;
}
}
// 区间查询:查询 [l, r] 内的最小值
int query(int u, int l, int r) {
// 如果当前节点区间完全包含在查询区间内,直接返回当前节点的最小值
if (bg[u] >= l && ed[u] <= r) {
return val[u];
}
pushdown(u); // 查询前先下传标记,确保子节点数据正确
int res = INF;
// 如果查询区间与左子节点有交集,递归查询左子树
if (l <= mid[u]) res = min(res, query(u * 2, l, r));
// 如果查询区间与右子节点有交集,递归查询右子树
if (r > mid[u]) res = min(res, query(u * 2 + 1, l, r));
return res;
}
// 区间更新:将 [l, r] 内的值都减 1
void update(int u, int l, int r) {
// 如果当前节点区间完全包含在更新区间内,直接更新当前节点并打上懒惰标记
if (bg[u] >= l && ed[u] <= r) {
work(u, 1); // 值减 1
return;
}
pushdown(u); // 更新前先下传标记
// 如果更新区间与左子节点有交集,递归更新左子树
if (l <= mid[u]) update(u * 2, l, r);
// 如果更新区间与右子节点有交集,递归更新右子树
if (r > mid[u]) update(u * 2 + 1, l, r);
pushup(u); // 回溯时更新父节点
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &c[i]);
}
build(1, 1, n); // 根据初始容量构建线段树
for (int i = 1; i <= m; i++) {
scanf("%d%d", &r[i].a, &r[i].b);
}
// 贪心策略:按请求的结束点 b 从小到大排序
sort(r + 1, r + m + 1, [](Request x, Request y) {
return x.b < y.b;
});
int ans = 0; // 记录满足的请求数量
// 遍历排序后的请求
for (int i = 1; i <= m; i++) {
// 查询该请求区间 [a, b] 内的最小畜栏容量
int s = query(1, r[i].a, r[i].b);
// 如果最小值大于0,说明区间内所有畜栏都至少有1个空位
if (s > 0) {
ans++; // 满足该请求
// 将该区间 [a, b] 内所有畜栏的容量减 1
update(1, r[i].a, r[i].b);
}
}
printf("%d\n", ans);
return 0;
}
习题:P1607 [USACO09FEB] Fair Shuttle G
解题思路
与 P1937 [USACO10MAR] Barn Allocation G 类似,都可以归结为带资源约束的区间调度问题。核心是决定以何种顺序处理奶牛们的乘车请求,以运送最多的奶牛。
同样地,解决此类问题的关键是找到正确的贪心策略。和上一题一样,最优的策略是按结束点排序,应该先考虑那些目的地更靠前的奶牛组。
首先,将所有 \(K\) 个奶牛组按照它们的终点站从小到大排序。用一个数据结构来维护 \(N-1\) 个路段上(因为到目的地就把此时的座位释放掉了),每个路段当前剩余的座位数。初始时,所有路段的剩余座位都是 \(C\)。按排好的顺序遍历每一个奶牛组,对于当前组,需要计算最多能让多少头奶牛上车。这个数量取决于两个因素:该组本身的人数、该组所需路段 \([S,E-1]\) 中,座位数最紧张(即剩余座位数最少)的那一段,这个“瓶颈”容量决定了最多能上车的奶牛数。所以,先查询 \([S,E-1]\) 这个路段区间内,最小的剩余座位数。那么,本组实际能上车的奶牛数是两者的较小值。将这个数字累加到总运送数中,并将 \([S,E-1]\) 区间内所有路段的剩余座位数都减去这个较小值。重复此过程,直到处理完所有奶牛组。
为了高效地实现“查询区间最小值”和“对区间进行减法更新”,可以使用带懒惰标记的线段树。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 2e4 + 5;
const int K = 5e4 + 5;
const int INF = 1e9;
// bg, ed, mid: 线段树节点对应的区间起点、终点、中点
// val: 线段树节点存储的区间最小值 (即区间内最少的剩余座位数)
// tag: 懒惰标记,记录区间被减去的总值
int bg[N * 4], ed[N * 4], mid[N * 4], val[N * 4], tag[N * 4];
// 定义奶牛组结构体
struct Group {
int s, e, m; // 起点站,终点站,奶牛数量
};
Group g[K];
// --- 线段树操作 ---
// 从子节点更新父节点的最小值
void pushup(int u) {
val[u] = min(val[u * 2], val[u * 2 + 1]);
}
// 构建线段树,所有路段初始容量为 c
void build(int u, int l, int r, int c) {
bg[u] = l; ed[u] = r; mid[u] = (l + r) / 2;
tag[u] = 0; // 初始化懒惰标记
if (l == r) { // 到达叶子节点,代表一个路段
val[u] = c;
return;
}
// 递归构建左右子树
build(u * 2, l, mid[u], c);
build(u * 2 + 1, mid[u] + 1, r, c);
pushup(u); // 回溯时更新父节点
}
// 对节点 u 应用更新操作(值减 d,标记加 d)
void work(int u, int d) {
val[u] -= d;
tag[u] += d;
}
// 向下传递懒惰标记
void pushdown(int u) {
if (tag[u] != 0) {
// 将父节点的标记传递给左右子节点
work(u * 2, tag[u]);
work(u * 2 + 1, tag[u]);
// 清除父节点的标记
tag[u] = 0;
}
}
// 区间查询:查询 [l, r] 内的最小值
int query(int u, int l, int r) {
// 如果当前节点区间完全包含在查询区间内,直接返回当前节点的最小值
if (bg[u] >= l && ed[u] <= r) {
return val[u];
}
pushdown(u); // 查询前先下传标记,确保子节点数据正确
int res = INF;
// 如果查询区间与左子节点有交集,递归查询左子树
if (l <= mid[u]) res = min(res, query(u * 2, l, r));
// 如果查询区间与右子节点有交集,递归查询右子树
if (r > mid[u]) res = min(res, query(u * 2 + 1, l, r));
return res;
}
// 区间更新:将 [l, r] 内的值都减去 change
void update(int u, int l, int r, int change) {
// 如果当前节点区间完全包含在更新区间内,直接更新当前节点并打上懒惰标记
if (bg[u] >= l && ed[u] <= r) {
work(u, change);
return;
}
pushdown(u); // 更新前先下传标记
// 如果更新区间与左子节点有交集,递归更新左子树
if (l <= mid[u]) update(u * 2, l, r, change);
// 如果更新区间与右子节点有交集,递归更新右子树
if (r > mid[u]) update(u * 2 + 1, l, r, change);
pushup(u); // 回溯时更新父节点
}
int main()
{
int k, n, c;
scanf("%d%d%d", &k, &n, &c); // k组, n站, c容量
// 构建线段树,代表 1 到 n-1 的路段,初始容量都为 c
// 注意:虽然站点是1到n,但路段是 n-1 个
build(1, 1, n - 1, c);
for (int i = 1; i <= k; i++) {
scanf("%d%d%d", &g[i].s, &g[i].e, &g[i].m);
}
// 贪心策略:按奶牛组的终点站 e 从小到大排序
sort(g + 1, g + k + 1, [](Group x, Group y) {
return x.e < y.e;
});
int ans = 0; // 记录运送的奶牛总数
// 遍历排序后的奶牛组
for (int i = 1; i <= k; i++) {
// 查询该组所需路段 [s, e-1] 上的最小剩余座位数
// 确定实际能上车的奶牛数,不能超过组里的人数和可用座位数
int change = min(query(1, g[i].s, g[i].e - 1), g[i].m);
if (change > 0) { // 如果能运送至少一头牛
ans += change; // 累加到总数
// 更新路段 [s, e-1] 的剩余座位数,减去 change
update(1, g[i].s, g[i].e - 1, change);
}
}
printf("%d\n", ans);
return 0;
}
对于要求支持区间查询的线段树,其结点上所维护的信息必须具有可合并性。也就是说,从某个结点的两个子结点的信息通过汇总操作可以得出该结点的信息。但有时所求的信息如果直接维护并不具有可合并性,这时可能需要维护一些额外的信息,从而使得子结点信息可以合并推出父结点信息。
例题:P4513 小白逛公园
给定一个长度为 \(n\) 的数列 \(a\),有 \(m\) 次操作,每次操作要么对 \(a\) 进行单点修改,要么查询数列 \(a\) 的最大子段和是多少。区间 \([l,r]\) 的连续和是指 \(\sum \limits_{i=l}^{r} a_i = a_l + a_{l+1} + \cdots + a_r\)。最大子段和指的是所有的区间连续和中最大的值。
数据范围:\(1 \le n \le 5 \times 10^5, 1 \le m \le 10^5, -1000 \le a_i \le 1000\)。
分析: 考虑对序列 \(a\) 建立线段树。如果只在结点上维护信息“当前区间内的最大子段和”,则无法汇总到父结点上。因为并不能通过“子结点的最大子段和”推出父结点的最大子段和。例如,对于序列 \(-1,1,1,-1\) 和序列 \(-1,1,-1,1\),两者的区间 \([1,2]\) 以及区间 \([3,4]\) 的最大子段和均为 \(1\),但是前者的区间 \([1,4]\) 的最大子段和为 \(2\),后者的为 \(1\)。
进一步地,考虑父结点的最大子段和只可能存在三种情况:是左子结点的最大子段和,是右子结点的最大子段和,是左子结点和右子结点的两段相邻的和拼起来。对于前两种情况很容易转移,现在考虑第三种情况。
在这种情况下,左子结点被拼起来的那一段区间必须包含左子结点的右端点,换句话说,它是以左子结点右端点为起点向左找的最大连续和,称之为最大后缀和;同理,右子结点被拼起来的那一段区间是以右子结点左端点为起点向右找的最大连续和,称为最大前缀和。这样只需维护结点的最大前缀和、最大后缀和以及最大子段和,就可以合并出父结点的最大子段和了。

进一步考虑如何合并出父结点的最大前缀和以及最大后缀和:对于父结点的最大前缀和,要么直接就是左子结点的最大前缀和,要么是左子结点的全体拼上右子结点的最大前缀和;最大后缀和的维护同理。

因此,只需要再维护一个区间和,就可以完成对最大前缀和、最大后缀和的维护了。显然区间和的维护直接合并两个子结点的区间和即可。
#include <cstdio>
#include <algorithm>
#define LC (cur * 2)
#define RC (cur * 2 + 1)
using namespace std;
const int N = 500005;
struct Node {
// sum是区间和,res是最大子段和
// lsum是最大前缀和,rsum是最大后缀和
int l, r, sum, res, lsum, rsum;
};
Node tree[N * 4];
int a[N];
void pushup(Node & cur, const Node & lc, const Node & rc) {
cur.sum = lc.sum + rc.sum;
cur.res = max(lc.rsum + rc.lsum, max(lc.res, rc.res));
cur.lsum = max(lc.lsum, lc.sum + rc.lsum);
cur.rsum = max(rc.rsum, lc.rsum + rc.sum);
}
void build(int cur, int l, int r) {
tree[cur].l = l; tree[cur].r = r;
if (l == r) {
tree[cur].sum = tree[cur].res = tree[cur].lsum = tree[cur].rsum = a[l];
return;
}
int mid = (l + r) / 2;
build(LC, l, mid); build(RC, mid + 1, r);
pushup(tree[cur], tree[LC], tree[RC]);
}
Node query(int cur, int l, int r) {
if (tree[cur].l >= l && tree[cur].r <= r) return tree[cur];
int mid = (tree[cur].l + tree[cur].r) / 2;
if (mid >= r) return query(LC, l, r);
else if (mid < l) return query(RC, l, r);
else {
Node res, resl = query(LC, l, r), resr = query(RC, l, r);
pushup(res, resl, resr);
return res;
}
}
void update(int cur, int p, int s) {
if (tree[cur].l == tree[cur].r && tree[cur].l == p) {
tree[cur].sum = tree[cur].res = tree[cur].lsum = tree[cur].rsum = s;
return;
}
int mid = (tree[cur].l + tree[cur].r) / 2;
if (mid >= p) update(LC, p, s);
else update(RC, p, s);
pushup(tree[cur], tree[LC], tree[RC]);
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
build(1, 1, n);
while (m--) {
int k, x, y;
scanf("%d%d%d", &k, &x, &y);
if (k == 1) {
if (x > y) swap(x, y);
printf("%d\n", query(1, x, y).res);
} else {
update(1, x, y);
}
}
return 0;
}
习题:P6492 [COCI 2010/2011 #6] STEP
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 200005;
int n, q;
bool a[MAXN]; // 0 代表 'L', 1 代表 'R'
// 线段树节点结构
struct Node {
int ans; // 区间内最长交替子串长度
int pref; // 区间最长交替前缀长度
int suff; // 区间最长交替后缀长度
int len; // 区间长度
bool lc; // 区间左端点字符
bool rc; // 区间右端点字符
};
Node tr[MAXN * 4]; // 线段树数组
// merge (pushup) 函数:合并左右子节点信息到父节点
Node merge(const Node& ls, const Node& rs) {
Node p;
p.len = ls.len + rs.len;
p.lc = ls.lc;
p.rc = rs.rc;
// 计算 ans: 可能是左子区间的 ans,右子区间的 ans,或者跨越中间的 ans
p.ans = max(ls.ans, rs.ans);
if (ls.rc != rs.lc) { // 如果中间可以连接
p.ans = max(p.ans, ls.suff + rs.pref);
}
// 计算 pref: 默认是左子区间的 pref
p.pref = ls.pref;
// 如果左子区间整个都是交替串,并且可以和右子区间连接
if (ls.pref == ls.len && ls.rc != rs.lc) {
p.pref += rs.pref;
}
// 计算 suff: 默认是右子区间的 suff
p.suff = rs.suff;
// 如果右子区间整个都是交替串,并且可以和左子区间连接
if (rs.suff == rs.len && ls.rc != rs.lc) {
p.suff += ls.suff;
}
return p;
}
// build: 构建线段树
void build(int p, int l, int r) {
tr[p].len = r - l + 1;
if (l == r) { // 叶子节点
tr[p].ans = tr[p].pref = tr[p].suff = 1;
tr[p].lc = tr[p].rc = a[l];
return;
}
int mid = l + (r - l) / 2;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
tr[p] = merge(tr[p * 2], tr[p * 2 + 1]);
}
// update: 单点更新
void update(int p, int l, int r, int pos) {
if (l == r) {
a[pos] = !a[pos]; // 翻转字符
tr[p].lc = tr[p].rc = a[pos];
// ans, pref, suff, len 对于单个字符的叶子节点始终是 1,无需更改
return;
}
int mid = l + (r - l) / 2;
if (pos <= mid) {
update(p * 2, l, mid, pos);
} else {
update(p * 2 + 1, mid + 1, r, pos);
}
// 回溯时合并信息
tr[p] = merge(tr[p * 2], tr[p * 2 + 1]);
}
int main() {
scanf("%d%d", &n, &q);
// 初始状态:序列全为 'L' (用 0 表示)
for (int i = 1; i <= n; ++i) {
a[i] = 0;
}
build(1, 1, n);
for (int i = 0; i < q; ++i) {
int x;
scanf("%d", &x);
update(1, 1, n, x);
// 根节点 tr[1] 的 ans 即为整个序列的答案
printf("%d\n", tr[1].ans);
}
return 0;
}
习题:P2894 [USACO08FEB] Hotel G
解题思路
维护每一段区间内的最大连续空房数,但是只维护这一个值是不够的,因为光从两个子区间的最大连续空房数中取最大值是不够的,也不能将两者直接相加,因为两个子区间里的最长连续空房不一定是挨着的。实际上除了从两个子区间的最大连续空房数中取最大值外,也有可能整个区间中的最长连续空房是横跨左右两个区间的,因此还需要维护区间内的前缀、后缀连续空房数量。因为还涉及区间更新操作,所以还需要一个延迟标记。
参考代码
#include <cstdio>
#include <algorithm>
#define LC (2 * u)
#define RC (2 * u + 1)
using std::max;
const int N = 50005;
struct Node {
int l, r, len;
int rest; // 区间内最长连续空房数
int pre, suf; // 前缀/后缀连续空房数
int flag; // 延迟标记
};
Node tree[N * 4];
void pushup(int u) {
tree[u].rest = max(tree[LC].suf + tree[RC].pre, max(tree[LC].rest, tree[RC].rest));
tree[u].pre = tree[LC].pre + (tree[LC].pre == tree[LC].len ? tree[RC].pre : 0);
tree[u].suf = tree[RC].suf + (tree[RC].suf == tree[RC].len ? tree[LC].suf : 0);
}
void work(int u, int flag) {
tree[u].flag = flag;
if (flag == 1) { // 入住
tree[u].rest = tree[u].pre = tree[u].suf = 0;
} else { // 退房
tree[u].rest = tree[u].pre = tree[u].suf = tree[u].len;
}
}
void pushdown(int u) {
if (tree[u].flag != 0) {
work(LC, tree[u].flag); work(RC, tree[u].flag);
tree[u].flag = 0;
}
}
void build(int u, int l, int r) {
tree[u].l = l; tree[u].r = r; tree[u].len = r - l + 1;
if (l == r) {
tree[u].rest = tree[u].pre = tree[u].suf = 1; // 初始均为空房
return;
}
int mid = (l + r) / 2;
build(LC, l, mid); build(RC, mid + 1, r);
pushup(u);
}
int query(int u, int x) {
if (tree[u].rest < x) return 0;
if (tree[u].len == 1) return tree[u].l;
pushdown(u);
// 如果左区间有足够的入住房间,只需在左区间内查询
if (tree[LC].rest >= x) return query(LC, x);
// 如果横跨左右区间能够提供足够的入住房间,则答案就是左子树区间后缀部分的起始位置
if (tree[LC].suf + tree[RC].pre >= x) return tree[LC].r - tree[LC].suf + 1;
return query(RC, x); // 否则只能考虑右区间
}
void update(int u, int l, int r, int val) {
if (tree[u].l >= l && tree[u].r <= r) {
work(u, val);
return;
}
pushdown(u);
int mid = (tree[u].l + tree[u].r) / 2;
if (mid >= l) update(LC, l, r, val);
if (mid + 1 <= r) update(RC, l, r, val);
pushup(u);
}
int main()
{
int n, m; scanf("%d%d", &n, &m);
build(1, 1, n);
while (m--) {
int i; scanf("%d", &i);
if (i == 1) {
int x; scanf("%d", &x);
int q = query(1, x);
printf("%d\n", q);
if (q != 0) update(1, q, q + x - 1, 1);
} else {
int x, y; scanf("%d%d", &x, &y);
y = x + y - 1;
update(1, x, y, -1);
}
}
return 0;
}
习题:P8233 [AGM 2022 资格赛] 区间
解题思路
用线段树维护区间合并信息,每个节点代表一个连续区间,存储以下信息:
sum:该区间内纯黑子区间的总数。llen:该区间从左端点开始,连续为黑色的长度。rlen:该区间从右端点开始,向左连续为黑色的长度。lazy:懒标记,用于高效地执行区间染黑操作。
当左子节点 lc 和右子节点 rc 的信息要合并到父节点 p 时:
p.sum:父节点的sum不仅是lc.sum + rc.sum,如果左子区间的右侧和右子区间的左侧能够拼接起来(即lc的后缀和rc的前缀都是黑色的),它们会形成一个新的、跨越两个子节点边界的黑色区间,这些新产生的子区间的数量为lc.rlen * rc.llen。因此,合并后的总和为lc.sum + rc.sum + lc.rlen * rc.llen。p.llen:父节点的左侧连续黑色长度,默认为lc.llen。但如果左子节点整个区间都是黑色的(即lc.llen == lc.total_length),那么这个连续黑色段就可以延伸到右子节点中,此时p.llen = lc.total_length + rc.llen。p.rlen:与p.llen的逻辑对称。
由于本题给出的坐标 \(l,r\) 的范围达到了 \(10^{18}\),需要离散化。假设离散化后有 \(m\) 个关键坐标点,可以将其分解成 \(2m-1\) 个小区间,第奇数个区间是关键坐标点本身,第偶数个区间是两个关键坐标点中间夹着的区间。
参考代码
#include <iostream>
#include <algorithm>
#include <utility>
using namespace std;
using ll = long long;
const int N = 1e6 + 5;
const int MOD = 1000000007;
const ll INV2 = 500000004;
// 辅助函数:计算 x*(x+1)/2 (mod MOD)
// 用于计算一个长度为 x 的纯黑区间所包含的子区间数量
int f(ll x) {
x %= MOD;
int res = 1ll * x * (x + 1) % MOD;
res = 1ll * res * INV2 % MOD;
return res;
}
struct Query {
int type;
ll l, r;
};
Query q[N];
// 线段树节点
struct Node {
int sum; // 区间内纯黑子区间的总数
ll llen; // 区间左侧连续为黑色的长度
ll rlen; // 区间右侧连续为黑色的长度
int lazy; // 懒标记 (1 表示整个区间被染黑)
};
ll coords[N * 2]; // 存储所有离散化后的坐标
Node tree[N * 16]; // 线段树
Node merge_nodes(const Node& left_node, const Node& right_node, ll left_len, ll right_len) {
Node res; res.lazy = 0;
// 1. 合并 sum:左右子树的 sum 再加上跨越中间边界形成的新子区间数 (lc.rlen * rc.llen)
res.sum = ((left_node.sum + right_node.sum) % MOD + ((left_node.rlen % MOD) * (right_node.llen % MOD) % MOD)) % MOD;
// 2. 合并 llen:如果左子节点全黑,则可以连接右子节点的左侧黑块
res.llen = left_node.llen;
if (left_node.llen == left_len) {
res.llen = (left_node.llen + right_node.llen);
}
// 3. 合并 rlen:如果右子节点全黑,则可以连接左子节点的右侧黑块
res.rlen = right_node.rlen;
if (right_node.rlen == right_len) {
res.rlen = (right_node.rlen + left_node.rlen);
}
return res;
}
pair<ll, ll> get_range(int i) {
// 奇数代表一个坐标点
if (i & 1) return {coords[i / 2 + 1], coords[i / 2 + 1]};
// 偶数代表两个坐标点之间的区间
else return {coords[i / 2] + 1, coords[i / 2 + 1] - 1};
}
void push_down(int u, int l, int r) {
if (tree[u].lazy == 0 || l == r) return;
int mid = l + (r - l) / 2;
ll left_len = get_range(mid).second - get_range(l).first + 1;
ll right_len = get_range(r).second - get_range(mid).second;
tree[u * 2].lazy = 1;
tree[u * 2].llen = left_len;
tree[u * 2].rlen = left_len;
tree[u * 2].sum = f(left_len);
tree[u * 2 + 1].lazy = 1;
tree[u * 2 + 1].llen = right_len;
tree[u * 2 + 1].rlen = right_len;
tree[u * 2 + 1].sum = f(right_len);
tree[u].lazy = 0; // 清除当前节点的懒标记
}
void push_up(int u, int l, int r) {
int mid = l + (r - l) / 2;
ll left_len = get_range(mid).second - get_range(l).first + 1;
ll right_len = get_range(r).second - get_range(mid).second;
tree[u] = merge_nodes(tree[u * 2], tree[u * 2 + 1], left_len, right_len);
}
void update(int u, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) {
tree[u].lazy = 1;
ll len = get_range(r).second - get_range(l).first + 1;
tree[u].llen = len;
tree[u].rlen = len;
tree[u].sum = f(len);
return;
}
push_down(u, l, r);
int mid = l + (r - l) / 2;
if (ql <= mid) update(u * 2, l, mid, ql, qr);
if (qr > mid) update(u * 2 + 1, mid + 1, r, ql, qr);
push_up(u, l, r);
}
Node query(int u, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) {
return tree[u];
}
push_down(u, l, r);
int mid = l + (r - l) / 2;
if (qr <= mid) {
return query(u * 2, l, mid, ql, qr);
}
if (ql > mid) {
return query(u * 2 + 1, mid + 1, r, ql, qr);
}
// 如果查询范围跨越了中间点,则需要合并左右子树的查询结果
Node left_res = query(u * 2, l, mid, ql, qr);
Node right_res = query(u * 2 + 1, mid + 1, r, ql, qr);
ll left_len = get_range(mid).second - get_range(l).first + 1;
ll right_len = get_range(r).second - get_range(mid).second;
return merge_nodes(left_res, right_res, left_len, right_len);
}
int main() {
int n;
scanf("%d", &n);
// --- 1. 离线处理:读入所有操作,并收集坐标点 ---
for (int i = 1; i <= n; ++i) {
scanf("%d%lld%lld", &q[i].type, &q[i].l, &q[i].r);
// 收集 l 和 r 作为关键坐标
coords[i * 2 - 1] = q[i].l;
coords[i * 2] = q[i].r;
}
// --- 2. 坐标离散化 ---
sort(coords + 1, coords + n * 2 + 1);
int m = unique(coords + 1, coords + n * 2 + 1) - coords - 1;
// lambda表达式,用于将原始坐标值转换为离散化后的秩 (1-based)
auto discrete = [&](ll x) {
return lower_bound(coords + 1, coords + m + 1, x) - coords;
};
// --- 3. 依次处理所有操作 ---
for (int i = 1; i <= n; i++) {
int l_rank = discrete(q[i].l) * 2 - 1;
int r_rank = discrete(q[i].r) * 2 - 1;
if (q[i].type == 1) { // 染色操作
update(1, 1, 2 * m - 1, l_rank, r_rank);
} else { // 查询操作
Node res = query(1, 1, 2 * m - 1, l_rank, r_rank);
printf("%d\n", res.sum);
}
}
return 0;
}
习题:P1471 方差
解题思路
本题要求对一个序列进行区间更新(区间加一个值)和区间查询(求平均数和方差)。
对于一个长度为 \(n\) 的子序列 \(A\)(从原序列的第 \(x\) 项到第 \(y\) 项),需要计算其平均数和方差。
- 平均数:\(\overline{A} = \dfrac{1}{n} \sum\limits_{i=x}^{y} A_i\),要计算平均数,只需要知道区间的和以及区间的长度 \(n = y - x + 1\)。
- 方差:方差的定义式为 \(s^2 = \dfrac{1}{n} \sum\limits_{i=x}^{y} \left( A_i - \overline{A} \right)^2\),直接使用这个公式计算效率较低,因为它需要先计算出平均数 \(\overline{A}\),然后再遍历一次序列。可以对公式进行展开和化简,得到一个更利于计算的形式:
根据这个化简后的公式,要计算方差,只需要知道区间的和以及区间的平方和(\(\sum A_i^2\)),以下分别记为 \(\text{sum}_1\) 和 \(\text{sum}_2\)。
操作 1 要求对区间 \([x,y]\) 内的每个数 \(A_i\) 都加上一个值 \(k\),需要知道这个操作如何影响 \(\text{sum}_1\) 和 \(\text{sum}_2\)。
设区间长度为 \(n\):
- 对 \(\text{sum}_1\) 的影响:\(\text{sum}_1' = \sum(A_i+k) = \sum A_i + \sum k = \text{sum}_1 + n \cdot k\)
- 对 \(\text{sum}_2\) 的影响:\(\text{sum}_2' = \sum(A_i+k)^2 = \sum(A_i^2 + 2kA_i + k^2) = \sum A_i^2 + 2k\sum A_i + \sum k^2 = \text{sum}_2 + 2k \cdot \text{sum}_1 + n \cdot k^2\)
可以发现,新区间的 \(\text{sum}_1'\) 和 \(\text{sum}_2'\) 可以由旧区间的 \(\text{sum}_1\) 和 \(\text{sum}_2\)、区间长度 \(n\) 和增量 \(k\) 计算得出,于是可以使用带有懒惰标记的线段树来维护。
参考代码
#include <cstdio>
#include <cmath>
#include <utility>
using namespace std;
const int MAXN = 100005;
int N, M;
double a[MAXN];
// 线段树节点结构
struct Node {
double sum1; // 区间和
double sum2; // 区间平方和
double lazy; // 懒惰标记
};
Node tr[MAXN * 4];
// pushup: 用子节点信息更新父节点
void pushup(int p) {
tr[p].sum1 = tr[p * 2].sum1 + tr[p * 2 + 1].sum1;
tr[p].sum2 = tr[p * 2].sum2 + tr[p * 2 + 1].sum2;
}
// 将懒惰标记 k 应用到节点 p
void apply_lazy(int p, int l, int r, double k) {
int len = r - l + 1;
// 更新 sum2,需要用到旧的 sum1,所以必须先更新 sum2
tr[p].sum2 += 2.0 * k * tr[p].sum1 + len * k * k;
// 更新 sum1
tr[p].sum1 += len * k;
// 累加懒惰标记
tr[p].lazy += k;
}
// pushdown: 将父节点的懒惰标记下推给子节点
void pushdown(int p, int l, int r) {
if (abs(tr[p].lazy) > 1e-9) { // 浮点数判断不为 0
int mid = l + (r - l) / 2;
apply_lazy(p * 2, l, mid, tr[p].lazy);
apply_lazy(p * 2 + 1, mid + 1, r, tr[p].lazy);
tr[p].lazy = 0.0;
}
}
// build: 构建线段树
void build(int p, int l, int r) {
tr[p].lazy = 0.0;
if (l == r) {
tr[p].sum1 = a[l];
tr[p].sum2 = a[l] * a[l];
return;
}
int mid = l + (r - l) / 2;
build(p * 2, l, mid);
build(p * 2 + 1, mid + 1, r);
pushup(p);
}
// update: 区间更新,给 [ul, ur] 区间每个数加上 k
void update(int p, int l, int r, int ul, int ur, double k) {
if (ul <= l && r <= ur) {
apply_lazy(p, l, r, k);
return;
}
pushdown(p, l, r);
int mid = l + (r - l) / 2;
if (ul <= mid) {
update(p * 2, l, mid, ul, ur, k);
}
if (ur > mid) {
update(p * 2 + 1, mid + 1, r, ul, ur, k);
}
pushup(p);
}
// query: 区间查询,返回 {sum1, sum2}
pair<double, double> query(int p, int l, int r, int ql, int qr) {
if (ql <= l && r <= qr) {
return {tr[p].sum1, tr[p].sum2};
}
pushdown(p, l, r);
int mid = l + (r - l) / 2;
double s1 = 0.0, s2 = 0.0;
if (ql <= mid) {
pair<double, double> left_res = query(p * 2, l, mid, ql, qr);
s1 += left_res.first;
s2 += left_res.second;
}
if (qr > mid) {
pair<double, double> right_res = query(p * 2 + 1, mid + 1, r, ql, qr);
s1 += right_res.first;
s2 += right_res.second;
}
return {s1, s2};
}
int main() {
scanf("%d%d", &N, &M);
for (int i = 1; i <= N; ++i) {
scanf("%lf", &a[i]);
}
build(1, 1, N);
for (int i = 0; i < M; ++i) {
int type; scanf("%d", &type);
if (type == 1) {
int x, y;
double k;
scanf("%d%d%lf", &x, &y, &k);
update(1, 1, N, x, y, k);
} else if (type == 2) {
int x, y;
scanf("%d%d", &x, &y);
pair<double, double> res = query(1, 1, N, x, y);
double len = y - x + 1;
printf("%.4f\n", res.first / len);
} else { // type == 3
int x, y;
scanf("%d%d", &x, &y);
pair<double, double> res = query(1, 1, N, x, y);
double len = y - x + 1;
double avg = res.first / len;
double var = res.second / len - avg * avg;
printf("%.4f\n", var);
}
}
return 0;
}
习题:P6477 [NOI Online #2 提高组] 子序列问题
解题思路
对于这类区间信息求和的问题,我们往往可以枚举一个端点(比如右端点),在一个数据结构上维护另一个端点取每个值时,该区间的答案。
这里我们考虑枚举右端点 \(r\),维护 \(l\) 取每个值的时候 \(f(l,r)\) 是多少。
如果问的是 \(f(l,r)\) 的和而不是平方和,则这个问题是很简单的(思考当枚举的右端点从 \(r-1\) 移动到 \(r\) 的时候,\(f\) 的值会怎么变化)。可以发现,这取决于上一个与 \(a_r\) 相等的数在哪个位置出现,如果 \(a_r\) 是第一次出现,则之前的每个 \(f\) 相当于都要加 \(1\),如果之前出现过 \(a_r\),则相当于前面部分的 \(f\) 不变(因为本来就有这个数),而后面部分的 \(f\) 都要加 \(1\)。
这样一来,问题就转化成了对一个序列支持两种操作:区间加 \(1\) 以及求整个区间的 \(f\) 的平方和。这个问题考虑用线段树来维护 \(l\) 取每个值时 \(f(l,r)\) 的平方和。
区间加 \(1\) 对区间中的平方和有什么样的影响?如果区间加 \(1\),平方和会增加 \(2 \times sum + len\),其中 \(sum\) 是区间和,\(len\) 是区间长度。因此只维护区间平方和不够,还需要维护一下区间和 \(sum\)。推广到区间加 \(add\) 对平方和的影响:若区间加 \(add\),则平方和会增加 \(2 \times d \times sum + d^2 \times len\)。
注意因为 \(a_i\) 很大,需要进行离散化。
参考代码
#include <cstdio>
#include <vector>
#include <algorithm>
#define LC (u * 2)
#define RC (u * 2 + 1)
using std::vector;
using std::lower_bound;
using std::sort;
using std::unique;
const int MOD = 1000000007;
const int N = 1e6 + 5;
int a[N], last[N];
vector<int> data;
int discretization(int x) {
return lower_bound(data.begin(), data.end(), x) - data.begin() + 1;
}
struct Node {
int l, r, len;
int sqr, add, sum;
};
Node tree[N * 4];
void pushup(int u) {
tree[u].sqr = (tree[LC].sqr + tree[RC].sqr) % MOD;
tree[u].sum = (tree[LC].sum + tree[RC].sum) % MOD;
}
void build(int u, int l, int r) {
tree[u].l = l; tree[u].r = r; tree[u].len = r - l + 1;
if (l == r) return;
int mid = (l + r) / 2;
build(LC, l, mid); build(RC, mid + 1, r);
}
void work(int u, int add) {
tree[u].sqr += 1ll * add * add % MOD * tree[u].len % MOD;
tree[u].sqr %= MOD;
tree[u].sqr += 2ll * add * tree[u].sum % MOD;
tree[u].sqr %= MOD;
tree[u].sum += 1ll * tree[u].len * add % MOD;
tree[u].sum %= MOD;
tree[u].add += add;
}
void pushdown(int u) {
if (tree[u].add != 0) {
work(LC, tree[u].add); work(RC, tree[u].add);
tree[u].add = 0;
}
}
void update(int u, int l, int r) {
if (tree[u].l >= l && tree[u].r <= r) {
work(u, 1);
return;
}
pushdown(u);
int mid = (tree[u].l + tree[u].r) / 2;
if (mid >= l) update(LC, l, r);
if (mid + 1 <= r) update(RC, l, r);
pushup(u);
}
int main()
{
int n; scanf("%d", &n);
build(1, 1, n);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]); data.push_back(a[i]);
}
sort(data.begin(), data.end());
data.erase(unique(data.begin(), data.end()), data.end());
for (int i = 1; i <= n; i++) a[i] = discretization(a[i]);
int ans = 0;
for (int i = 1; i <= n; i++) {
int pre = last[a[i]];
update(1, pre + 1, i);
ans += tree[1].sqr; ans %= MOD;
last[a[i]] = i;
}
printf("%d\n", ans);
return 0;
}
线段树优化动态规划
动态规划是解决最优化问题的重要工具,许多 DP 问题的状态转移方程可以写成这种形式:\(f_i = \min \{ f_j \} + \text{cost}(j,i)\),其中 \(0 \le j \lt i\)。
在这种形式下,为了计算 \(f_i\),需要遍历所有可能的 \(j\) 来寻找最优决策。如果 \(i\) 的范围是 \(n\),那么这种朴素的实现通常会导致 \(O(n^2)\) 的总时间复杂度。在很多题目中,\(n\) 的范围可能达到 \(10^5\) 或更大,\(O(n^2)\) 的算法将无法在规定时间内完成。
此时,就需要对 DP 的状态转移过程进行优化。一个常见的优化方向是,能否在比 \(O(n)\) 更快的时间内,找到使 \(f_j\) 最优的那个决策点 \(j\)?如果决策点的选择依赖于某个值的范围查询,那么线段树就成了一个非常有力的优化工具。
例题:P2418 yyy loves OI IV
这是一个典型的动态规划问题,目标是求一个序列的最小划分数,其中每个划分的子序列需要满足特定条件。
可以定义 \(f_i\) 为将前 \(i\) 名学生分组所需的最少宿舍数量,最终的答案就是 \(f_n\)。
状态转移方程可以这样构想:\(f_i = 1 + \min \{ f_j \}\),其中 \(0 \le j \lt i\) 且从 \(j+1\) 到 \(i\) 的学生可以合法地分在同一个宿舍。
一个朴素的解法是,对于每个 \(i\),遍历所有可能的 \(j\),其中 \(j\) 从 \(0\) 到 \(i-1\),检查 \([j+1,i]\) 区间的合法性,然后更新 \(f_i\)。检查合法性需要统计区间内两种学生的人数,可以用前缀和优化到 \(O(1)\)。但总体复杂度仍为 \(O(n^2)\),对于 \(n = 5 \times 10^5\) 的数据规模会超时。因此,必须优化寻找 \(\min \{f_j\}\) 的过程。
优化的关键在于快速找到满足条件的 \(\min\{f_j\}\),一个宿舍 \([j+1,i]\) 合法的条件是三者之一,可以分别对这三个条件进行优化,然后取其中的最小值。
令 \((\text{pref}_1)_k\) 为前 \(k\) 个学生中膜拜 yyy 的人数,\((\text{pref}_2)_k\) 为膜拜 c01 的人数,一个区间 \([j+1,i]\) 合法的三个条件可以表示为:
- 全为 c01:\((\text{pref}_1)_i - (\text{pref}_1)_j = 0 \Rightarrow (\text{pref}_1)_i = (\text{pref}_1)_j\)
- 全为 yyy:\((\text{pref}_2)_i - (\text{pref}_2)_j = 0 \Rightarrow (\text{pref}_2)_i = (\text{pref}_2)_j\)
- 人数差绝对值 \(\le m\):\(|((\text{pref}_1)_i - (\text{pref}_1)_j) - ((\text{pref}_2)_i - (\text{pref}_2)_j)| \le m\)
可以为这三个条件分别寻找最优的 \(j\):
- 对于条件 1 \((\text{pref}_1)_i = (\text{pref}_1)_j\),需要在所有满足 \(\text{pref}_1\) 值与 \((\text{pref}_1)_{i}\) 相同的 \(j\) 中,找到 \(f_{j}\) 的最小值。这可以通过一个辅助数组 \(p_1\) 来实现,\((p_1)_k\) 记录所有 \(\text{pref}_1\) 值为 \(k\) 的位置中最小的 \(f\) 值。在计算 \(f_i\) 时,直接查询 \((p_1)_{(\text{pref}_1)_i}\) 即可,这是 \(O(1)\) 的操作。
- 对于条件 2 \((\text{pref}_2)_i = (\text{pref}_2)_j\),同理,用另一个辅助数组 \(p_2\) 来记录,查询 \((p_2)_{(\text{pref}_2)_i}\) 也是 \(O(1)\) 的。
- 对于条件 3,可以进一步转换。令 \(d_k = (\text{pref}_1)_k - (\text{pref}_2)_k\),则条件变为 \(|d_i - d_j| \le m\),也就是 \(d_i - m \le d_j \le d_i + m\)。需要在所有 \(j \lt i\) 中,找出 \(d_j\) 值落在 \([d_i - m, d_i + m]\) 区间内的最小 \(f_j\)。这是一个经典的 RMQ 问题,可以使用线段树来解决。\(d_k\) 的值域为 \([-k,k]\),所以需要将 \([-n,n]\) 的范围映射到线段树的 \([0,2n]\) 索引上(例如加上偏移量 \(n\)),线段树的每个节点存储对应 \(d\) 值范围内的最小 \(f\) 值。
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 5e5 + 5;
const int INF = 1e9;
// s: 存储学生序列, 1或2
// pref1/pref2: 膜拜1/2的人数的前缀和
// diff: pref1[i] - pref2[i]
// dp: dp[i]表示前i个学生分组所需的最少宿舍数
// p1/p2: 优化用的辅助数组
int s[N], pref1[N], pref2[N], diff[N], dp[N], p1[N], p2[N];
int val[N * 8]; // 线段树, 用于优化差值条件的查询
// 线段树向上更新
void pushup(int u) {
val[u] = min(val[u * 2], val[u * 2 + 1]);
}
// 构建线段树, 初始化为无穷大
void build(int u, int l, int r) {
if (l == r) {
val[u] = INF;
return;
}
int mid = l + (r - l) / 2;
build(u * 2, l, mid);
build(u * 2 + 1, mid + 1, r);
pushup(u);
}
// 在[ql, qr]区间内查询最小值
int query(int u, int l, int r, int ql, int qr) {
if (l >= ql && r <= qr) {
return val[u];
}
int mid = l + (r - l) / 2;
int res = INF;
if (ql <= mid) res = min(res, query(u * 2, l, mid, ql, qr));
if (qr > mid) res = min(res, query(u * 2 + 1, mid + 1, r, ql, qr));
return res;
}
// 单点更新: 将pos位置的值更新为min(current_value, x)
void update(int u, int l, int r, int pos, int x) {
if (l == r) {
val[u] = min(val[u], x);
return;
}
int mid = l + (r - l) / 2;
if (pos <= mid) update(u * 2, l, mid, pos, x);
else update(u * 2 + 1, mid + 1, r, pos, x);
pushup(u);
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &s[i]);
}
// 预处理前缀和与差值
for (int i = 1; i <= n; i++) {
pref1[i] = pref1[i - 1] + (s[i] == 1);
pref2[i] = pref2[i - 1] + (s[i] == 2);
diff[i] = pref1[i] - pref2[i];
}
// 初始化
for (int i = 1; i <= n; i++) {
dp[i] = p1[i] = p2[i] = INF;
}
// diff的范围是[-n, n], 线段树下标映射到[0, 2n]
build(1, 0, 2 * n);
// DP边界条件
dp[0] = 0;
p1[pref1[0]] = 0; // pref1[0]=0, p1[0]存dp[0]
p2[pref2[0]] = 0; // pref2[0]=0, p2[0]存dp[0]
update(1, 0, 2 * n, diff[0] + n, 0); // diff[0]=0, 在线段树的n位置存dp[0]
// 动态规划
for (int i = 1; i <= n; i++) {
int res = INF; // res用于寻找满足条件的min(dp[j])
// 条件1: 区间[j+1, i]全为2, 等价于 pref1[i] == pref1[j]
// p1[k] 存储 pref1值为k的所有位置的最小dp值
res = min(res, p1[pref1[i]]);
// 条件2: 区间[j+1, i]全为1, 等价于 pref2[i] == pref2[j]
// p2[k] 存储 pref2值为k的所有位置的最小dp值
res = min(res, p2[pref2[i]]);
// 条件3: abs(count1 - count2) <= M, 等价于 abs(diff[i] - diff[j]) <= M
int d = diff[i] + n; // 当前diff值+偏移量
int low = max(0, d - m);
int high = min(2 * n, d + m);
// 在线段树上查询 diff[j] 在 [diff[i]-m, diff[i]+m] 范围内的最小dp[j]
res = min(res, query(1, 0, 2 * n, low, high));
// 状态转移
if (res != INF) {
dp[i] = res + 1;
}
// 用新计算出的dp[i]更新辅助数据结构
if (dp[i] != INF) {
p1[pref1[i]] = min(p1[pref1[i]], dp[i]);
p2[pref2[i]] = min(p2[pref2[i]], dp[i]);
update(1, 0, 2 * n, d, dp[i]);
}
}
printf("%d\n", dp[n]);
return 0;
}
扫描线
例:P5490 【模板】扫描线
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 100005;
int y[MAXN * 2], ylen;
struct Node {
int l, r, len, cnt;
};
Node tree[MAXN * 8];
struct Line {
int x, y1, y2, flag;
bool operator<(const Line& other) const {
return x < other.x;
}
};
Line line[MAXN * 2];
void build(int cur, int l, int r) {
tree[cur].l = l; tree[cur].r = r;
if (l + 1 == r) return;
int mid = (l + r) / 2;
build(cur * 2, l, mid); build(cur * 2 + 1, mid, r);
}
void pushup(int cur) {
if (tree[cur].cnt) tree[cur].len = y[tree[cur].r] - y[tree[cur].l];
else if (tree[cur].l + 1 == tree[cur].r) tree[cur].len = 0;
else tree[cur].len = tree[cur * 2].len + tree[cur * 2 + 1].len;
}
void update(int cur, int l, int r, int d) {
if (tree[cur].r <= l || tree[cur].l >= r) return;
if (tree[cur].l >= l && tree[cur].r <= r) {
tree[cur].cnt += d; pushup(cur); return;
}
update(cur * 2, l, r, d); update(cur * 2 + 1, l, r, d);
pushup(cur);
}
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
line[i] = {x1, y1, y2, 1}; line[n + i] = {x2, y1, y2, -1};
y[i] = y1; y[n + i] = y2;
}
n *= 2;
sort(line + 1, line + n + 1);
sort(y + 1, y + n + 1);
ylen = unique(y + 1, y + n + 1) - y - 1;
build(1, 1, ylen);
LL ans = 0;
for (int i = 1; i < n; i++) {
int y1 = lower_bound(y + 1, y + ylen + 1, line[i].y1) - y;
int y2 = lower_bound(y + 1, y + ylen + 1, line[i].y2) - y;
update(1, y1, y2, line[i].flag);
ans += 1ll * (line[i + 1].x - line[i].x) * tree[1].len;
}
printf("%lld\n", ans);
return 0;
}
例:P3875 [TJOI2010] 被污染的河流
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 10005;
struct Line {
int x, y1, y2, flag;
bool operator<(const Line& other) const {
return x < other.x;
}
} line[MAXN * 2];
int y[MAXN * 2], cnt;
struct Node {
int l, r, len, cnt;
} tree[MAXN * 8];
void pushup(int cur) {
if (tree[cur].cnt) tree[cur].len = y[tree[cur].r] - y[tree[cur].l];
else if (tree[cur].l + 1 == tree[cur].r) tree[cur].len = 0;
else tree[cur].len = tree[cur * 2].len + tree[cur * 2 + 1].len;
}
void build(int cur, int l, int r) {
tree[cur] = {l, r, 0, 0};
if (l + 1 == r) return;
int mid = (l + r) / 2;
build(cur * 2, l, mid);
build(cur * 2 + 1, mid, r);
}
void update(int cur, int l, int r, int d) {
if (tree[cur].l >= r || tree[cur].r <= l) return;
if (tree[cur].l >= l && tree[cur].r <= r) {
tree[cur].cnt += d;
pushup(cur); return;
}
update(cur * 2, l, r, d); update(cur * 2 + 1, l, r, d);
pushup(cur);
}
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
if (x1 == x2) {
line[i] = {x1 - 1, min(y1, y2), max(y1, y2), 1};
line[i + n] = {x1 + 1, min(y1, y2), max(y1, y2), -1};
y[i] = min(y1, y2); y[i + n] = max(y1, y2);
} else {
line[i] = {min(x1, x2), y1 - 1, y1 + 1, 1};
line[i + n] = {max(x1, x2), y1 - 1, y1 + 1, -1};
y[i] = y1 - 1; y[i + n] = y1 + 1;
}
}
sort(line + 1, line + 2 * n + 1);
sort(y + 1, y + 2 * n + 1);
cnt = unique(y + 1, y + 2 * n + 1) - y - 1;
build(1, 1, cnt);
int ans = 0;
for (int i = 1; i < n * 2; i++) {
int y1 = lower_bound(y + 1, y + cnt + 1, line[i].y1) - y;
int y2 = lower_bound(y + 1, y + cnt + 1, line[i].y2) - y;
update(1, y1, y2, line[i].flag);
ans += (line[i + 1].x - line[i].x) * tree[1].len;
}
printf("%d\n", ans);
return 0;
}
例:P1502 窗口的星星
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 20005;
struct Line {
LL x, y1, y2, d, flag;
bool operator<(const Line& other) const {
// 注意对于两条x相等的扫描线,应先处理引入星星的扫描线
return x != other.x ? x < other.x : flag > other.flag;
}
};
Line line[MAXN];
LL c[MAXN];
struct Node {
int l, r;
LL res, add;
};
Node tree[MAXN * 4];
void pushup(int cur) {
tree[cur].res = max(tree[cur * 2].res, tree[cur * 2 + 1].res);
}
void pushdown(int cur) {
if (tree[cur].l != tree[cur].r) {
tree[cur * 2].res += tree[cur].add;
tree[cur * 2 + 1].res += tree[cur].add;
tree[cur * 2].add += tree[cur].add;
tree[cur * 2 + 1].add += tree[cur].add;
tree[cur].add = 0;
}
}
void build(int cur, int l, int r) {
tree[cur] = {l, r, 0, 0};
if (l == r) return;
int mid = (l + r) / 2;
build(cur * 2, l, mid); build(cur * 2 + 1, mid + 1, r);
pushup(cur);
}
void update(int cur, int l, int r, LL d) {
if (tree[cur].l > r || tree[cur].r < l) return;
if (tree[cur].l >= l && tree[cur].r <= r) {
tree[cur].res += d; tree[cur].add += d;
return;
}
pushdown(cur);
update(cur * 2, l, r, d); update(cur * 2 + 1, l, r, d);
pushup(cur);
}
int main()
{
int t;
scanf("%d", &t);
while (t--) {
int n, w, h;
scanf("%d%d%d", &n, &w, &h);
for (int i = 1; i <= n; i++) {
LL x, y, l;
scanf("%lld%lld%lld", &x, &y, &l);
line[i] = {x, y, y + h - 1, l, 1};
line[n + i] = {x + w - 1, y, y + h - 1, l, -1};
c[i] = y; c[n + i] = y + h - 1;
}
sort(line + 1, line + 2 * n + 1);
sort(c + 1, c + 2 * n + 1);
int len = unique(c + 1, c + 2 * n + 1) - c - 1;
build(1, 1, len);
LL ans = 0;
for (int i = 1; i < 2 * n; i++) {
int y1 = lower_bound(c + 1, c + len + 1, line[i].y1) - c;
int y2 = lower_bound(c + 1, c + len + 1, line[i].y2) - c;
update(1, y1, y2, line[i].d * line[i].flag);
ans = max(ans, tree[1].res);
}
printf("%lld\n", ans);
}
return 0;
}
例:P1856 [IOI1998] [USACO5.5] 矩形周长Picture
参考代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 10005;
struct Line {
int x, y1, y2, flag;
bool operator<(const Line& other) const {
return x != other.x ? x < other.x : flag > other.flag;
}
};
Line lx[MAXN], ly[MAXN];
int x[MAXN], y[MAXN], xlen, ylen;
struct Node {
int l, r, cnt, len;
};
Node tree[MAXN * 4];
void pushup(int cur, int a[]) {
if (tree[cur].cnt) tree[cur].len = a[tree[cur].r] - a[tree[cur].l];
else if (tree[cur].l + 1 == tree[cur].r) tree[cur].len = 0;
else tree[cur].len = tree[cur * 2].len + tree[cur * 2 + 1].len;
}
void build(int cur, int l, int r, int a[]) {
tree[cur].l = l; tree[cur].r = r;
if (l + 1 == r) return;
int mid = (l + r) / 2;
build(cur * 2, l, mid, a); build(cur * 2 + 1, mid, r, a);
}
void update(int cur, int l, int r, int d, int a[]) {
if (tree[cur].l >= r || tree[cur].r <= l) return;
if (tree[cur].l >= l && tree[cur].r <= r) {
tree[cur].cnt += d; pushup(cur, a); return;
}
update(cur * 2, l, r, d, a); update(cur * 2 + 1, l, r, d, a);
pushup(cur, a);
}
int main()
{
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
lx[i] = {x1, y1, y2, 1}; lx[n + i] = {x2, y1, y2, -1};
ly[i] = {y1, x1, x2, 1}; ly[n + i] = {y2, x1, x2, -1};
x[i] = x1; x[n + i] = x2; y[i] = y1; y[n + i] = y2;
}
n *= 2;
sort(x + 1, x + n + 1); xlen = unique(x + 1, x + n + 1) - x - 1;
sort(y + 1, y + n + 1); ylen = unique(y + 1, y + n + 1) - y - 1;
sort(lx + 1, lx + n + 1); sort(ly + 1, ly + n + 1);
build(1, 1, ylen, y);
int ans = 0;
for (int i = 1; i <= n; i++) {
int y1 = lower_bound(y + 1, y + ylen + 1, lx[i].y1) - y;
int y2 = lower_bound(y + 1, y + ylen + 1, lx[i].y2) - y;
int pre = tree[1].len;
update(1, y1, y2, lx[i].flag, y);
ans += abs(tree[1].len - pre);
}
build(1, 1, xlen, x);
for (int i = 1; i <= n; i++) {
int x1 = lower_bound(x + 1, x + xlen + 1, ly[i].y1) - x;
int x2 = lower_bound(x + 1, x + xlen + 1, ly[i].y2) - x;
int pre = tree[1].len;
update(1, x1, x2, ly[i].flag, x);
ans += abs(tree[1].len - pre);
}
printf("%d\n", ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号