二分查找与二分答案
“猜数字游戏”：在心里想一个不超过 \(1000\) 的正整数，每猜一个数回答“大一些”、“小一些”或者“正好猜中”，则可以保证在 \(10\) 次之内猜到它。
这里的猜法就是“二分”。首先猜 \(500\)，如果运气很好那就直接猜中，否则不管回答是“太大”还是“太小”，都能把可行范围缩小一半：如果“太大”，那么答案在 \(1 \sim 499\) 之间；如果“太小”，那么答案在 \(501 \sim 1000\) 之间。只要每次选择可行区间的中点去猜，每次都可以把范围缩小一半。由于 \(\log_2 1000 < 10\)，最多 \(10\) 次一定能猜到。
二分查找
例题：P2249 [深基13.例1] 查找
输入 \(n \ (n \le 10^6)\) 个不超过 \(10^9\) 的单调不减的非负整数 \(a_1,a_2,\cdots,a_n\)，然后进行 \(m \ (m \le 10^5)\) 次询问。对于每次询问，给出一个整数 \(q \ (q \le 10^9)\)，要求输出这个数字在序列中第一次出现的编号，如果没有找到，则输出 \(-1\)。
分析：对于每次询问，直接从头到尾找一遍数字是不可行的，这样时间复杂度就是 \(O(mn)\)，效率太低。而且，这种做法没有利用好题目给出的一个条件：保证序列元素为升序。利用这个条件，能否得到时间复杂度更优的做法呢？
利用二分的思想就可以加速查找过程，每次取中间元素和待查找数据进行比较，如果正好相等那就找到了，如果待查找元素更小，则在左半部分继续用这个方式查找，更大则在右半部分查找。
#include <cstdio>
const int N = 1e6 + 5;
int a[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
for (int i = 1; i <= m; i++) {
int q; scanf("%d", &q);
int l = 1, r = n;
bool ok = false;
while (l <= r) {
int mid = (l + r) / 2; // 取中点
if (q == a[mid]) { // 刚好找到要找的数字
printf("%d ", mid); ok = true; break;
} else if (q < a[mid]) { // 取区间的前一半
r = mid - 1;
} else { // 取区间的后一半
l = mid + 1;
}
}
if (!ok) printf("-1 ");
}
return 0;
}
但是这个程序并不能通过样例数据。例如对于序列 \([1,3,3,3,5,7,9,11,13,15,15]\)，当要查找数据 \(3\) 时，上面这个程序对应的输出结果是 \(3\)，因为第一轮取到的中点是 \(a_6\)，\(3 < a_6\)，于是第二轮在左半区继续查找，取中点 \(a_3\)，\(a_3\) 刚好等于 \(3\)，于是查找成功，输出此时的位置 \(3\)。但是题目要求的是第一次出现的位置编号，也就是需要输出 \(2\)。事实上，这个程序仅在序列中的数字中都不相同时才是对的，如果出现重复的数字，则这个程序输出的是查找过程中第一次查找到指定数据的位置而不是原序列中第一次出现（最左边）的位置。
要正确地解决这个问题，首先需要将问题转化一下，如果要找某个数 \(x\) 第一次出现的位置，等价于找到原序列中 \(<x\) 和 \(\ge x\) 的分界线，于是我们需要把二分过程中的三个分支转化成两个分支。
#include <cstdio>
const int N = 1e6 + 5;
int a[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
for (int i = 1; i <= m; i++) {
int q; scanf("%d", &q);
int l = 1, r = n;
while (l <= r) {
int mid = (l + r) / 2;
if (a[mid] < q) {
l = mid + 1;
} else {
r = mid - 1;
}
}
// 最后分界线两侧为 r | l
// 左侧 <q，右侧 >=q
// 因此要查找某个数在序列中第一次出现的位置，对最终的 a[l] 进行判断
if (l <= n && a[l] == q) printf("%d ", l); // 注意要判断l<=n，因为可能q比所有的元素都大
else printf("-1 ");
}
return 0;
}
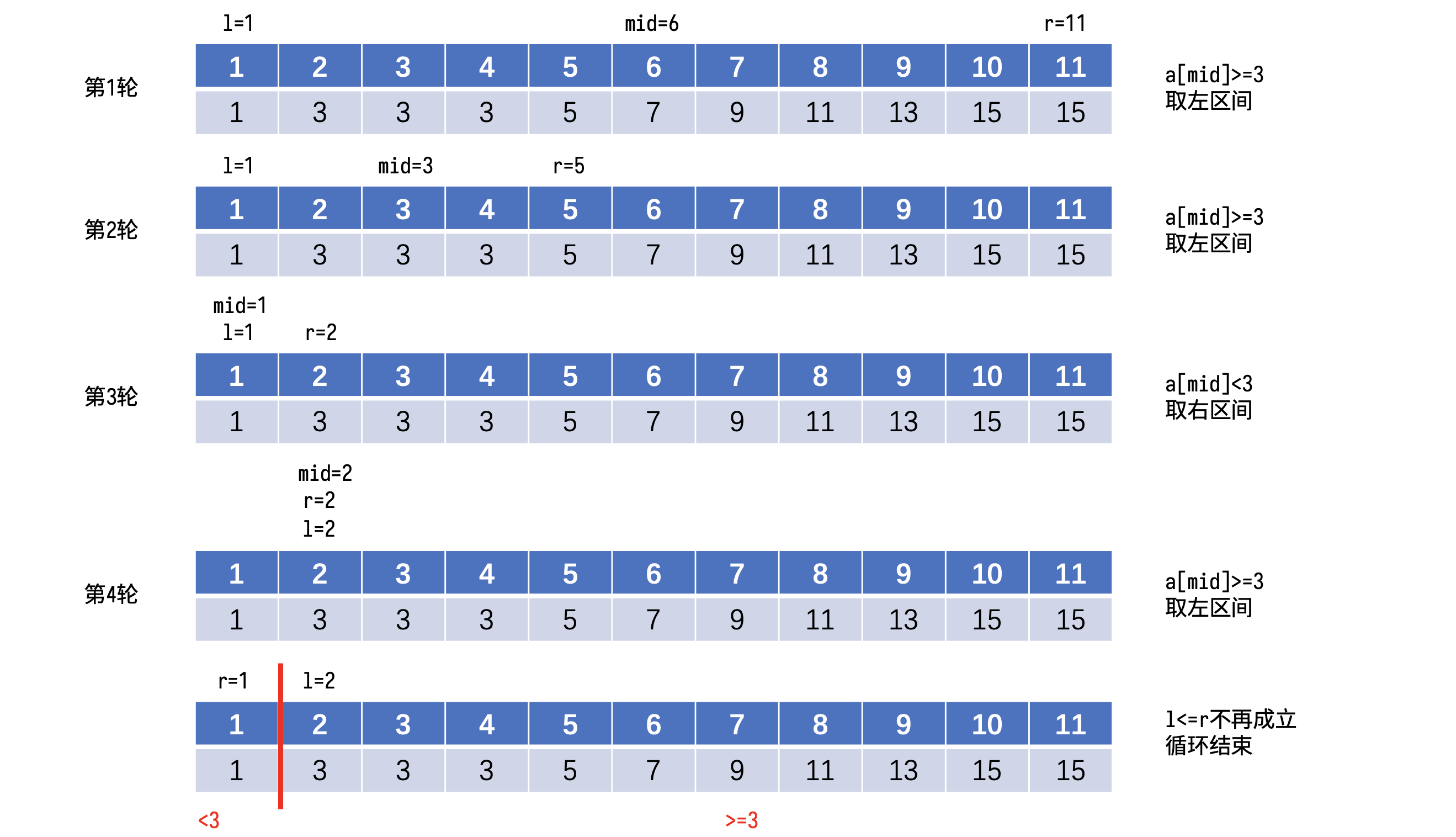
由于每轮二分区间长度都要衰减一半，因此二分查找的时间复杂度是 \(O(\log n)\)，相比于直接从头到尾查找的 \(O(n)\) 有了很大的改进。
在 C++ 标准模板库（STL）中针对二分查找有两个相关函数 lower_bound() 和 upper_bound()，用到的头文件是 algorithm：
lower_bound(begin,end,val)在值有序的数组连续地址[begin,end)中找到第一个大于等于 \(val\) 的位置并返回其地址upper_bound(begin,end,val)在值有序的数组连续地址[begin,end)中找到第一个大于 \(val\) 的位置并返回其地址
如果对“地址”的概念不理解，可以先认为这个返回值减去数组名刚好等于对应的数组下标。如果不存在大于等于/大于 val 的元素，则返回尾指针或尾迭代器。如果要找最后一个小于或小于等于 val 的，可以在 lower_bound 或 upper_bound 的结果上自减，但要注意自减前先判断是否已经是开头位置。
lower_bound 能找到某数第一次出现的位置，upper_bound 能找到某数最后一次出现的位置的下一个位置，那么某个数出现的次数可以表示为 upper_bound(...)-lower_bound(...)。
利用标准库，之前的例题可以写得更加精简：
#include <cstdio>
#include <algorithm>
using std::lower_bound;
const int N = 1e6 + 5;
int a[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
for (int i = 1; i <= m; i++) {
int q; scanf("%d", &q);
// 返回 a[1]~a[n] 中 >=q 的第一个位置的地址，减去数组名 a 后相当于对应下标
int idx = lower_bound(a + 1, a + n + 1, q) - a;
if (idx <= n && a[idx] == q) printf("%d ", idx);
else printf("-1 ");
}
return 0;
}
另外，如果只需要知道有序序列中是否包含某个元素，可以使用 binary_search 这个函数，用法与 lower_bound 和 upper_bound 类似，只不过返回值是布尔型，找得到返回 true，找不到返回 false。
习题：P1678 烦恼的高考志愿
解题思路
将每个学校的分数线排序，此时对于每位同学的估分 \(x\)，相当于从学校分数线中找到与其最接近的，这个问题等价于在有序数组中找到第一个 \(\ge x\) 的位置和最后一个 $ <x $ 的位置，这一点可以利用二分查找实现。要注意两种极端情况，估分比每一所学校的分数线都要高或低，此时找最接近的分数线相当于只需要考虑其中一种。
#include <cstdio>
#include <algorithm>
using ll = long long;
using std::sort;
using std::lower_bound;
using std::min;
const int N = 1e5 + 5;
const int INF = 1e7;
int a[N];
int main()
{
int m, n; scanf("%d%d", &m, &n);
for (int i = 1; i <= m; i++) scanf("%d", &a[i]);
sort(a + 1, a + m + 1);
ll ans = 0;
for (int i = 1; i <= n; i++) {
int b; scanf("%d", &b);
int diff = INF;
int idx = lower_bound(a + 1, a + m + 1, b) - a; // 第一个>=b的位置
if (idx <= m) diff = min(diff, a[idx] - b);
idx--; // 最后一个<b的位置
if (idx >= 1) diff = min(diff, b - a[idx]);
// 取分差小的加到答案中
ans += diff;
}
printf("%lld\n", ans);
return 0;
}
习题：P1978 集合
解题思路
题意概括一下就是如果 \(x\) 被选入集合，那么 \(kx\) 不能被选入集合，问最多能选多少个数。
比如当 \(k=3\) 时，如果有五个数分别为 \([1,3,9,27,81]\)，则应该选 \([1,9,81]\) 而不是选 \([3,27]\)，从这个例子中可以发现，应该从小到大依次考虑每个数是否可以被选入集合。注意数据范围，如果针对每个数 \(x\) 去计算 \(kx\) 可能会超出 long long 的范围。不妨反过来考虑，从小到大依次考虑每个数是否选入集合，如果这个数不是 \(k\) 的倍数，那它必然可以选入集合，如果它是 \(k\) 的倍数则要看 \(x / k\) 是否已经被选入集合（这样就规避了溢出的风险），这一点只需要维护已经被选入集合的数字并利用二分查找检查某个数是否在里面即可。
#include <cstdio>
#include <algorithm>
using std::sort;
using std::lower_bound;
using ll = long long;
const int N = 100005;
ll a[N], chosen[N]; // chosen记录已被选入集合的数
int main()
{
int n, k;
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) scanf("%lld", &a[i]);
sort(a + 1, a + n + 1);
int cnt = 0; // 已被选入集合的数的个数
for (int i = 1; i <= n; i++) {
if (a[i] % k != 0) {
cnt++; chosen[cnt] = a[i];
} else {
int idx = lower_bound(chosen + 1, chosen + cnt + 1, a[i] / k) - chosen;
if (idx > cnt || chosen[idx] != a[i] / k) { // 在已选入集合的数字中没有找到a[i]/k
cnt++; chosen[cnt] = a[i];
}
}
}
printf("%d\n", cnt);
return 0;
}
大多数人学习二分查找时，得到的第一个概念是“它必须在有序数组上使用”。这虽然没错，但只是二分查找能力的一个特例。
二分查找的真正本质是：能够通过检查中间的一个点，就可靠地将查找空间缩减一半。
“寻找峰值”问题
定义：一个“峰值”元素是指比它的直接相邻元素都大的元素。在一个数组 \(arr\) 中，如果 \(arr_i \gt arr_{i-1}\) 并且 \(arr_i \gt arr_{i+1}\)，那么 \(arr_i\) 就是一个峰值。对于数组边界上的元素，只需要和它的一个方向的邻居比较。
这个数组是无序的，但它有一个可以利用的关键特性。
在数组中任选一个中间点 \(arr_{mid}\)，然后检查它的邻居：
- 如果 \(arr_{mid} \lt arr_{mid+1}\)：这说明 \(mid\) 右边的元素更大，形成了一个“上坡”。既然数组是有限的，这个“上坡”不可能永远持续下去，它最终必然会停止（要么到达数组末尾，要么开始下降）。因此，在右半边必定存在一个峰值。可以放心地抛弃包括 \(mid\) 在内的整个左半部分。
- 如果 \(arr_{mid} \gt arr_{mid+1}\)：这说明 \(mid\) 右边的元素更小，形成了一个“下坡”。这意味着 \(mid\) 本身可能就是一个峰值，或者峰值在它的左边（因为左边可能也是一个“上坡”）。无论哪种情况，在左半部分（包含 \(mid\)）必定存在一个峰值。可以放心地抛弃 \(mid\) 右边的所有部分。
发现了吗？在每一步，只要没找到峰值，总能把查找范围缩小一半。这恰好满足了二分查找的前提条件。
#include <cstdio>
#include <vector>
using std::vector;
int findPeakElement(const vector<int> &arr) {
int n = arr.size();
if (n == 0) return -1;
if (n == 1) return 0; // 唯一的元素就是峰值
int l = 0, r = n - 1;
while (l < r) { // 当 l 和 r 相遇时，循环终止
int mid = l + (r - l) / 2;
// 核心逻辑：将中间值与它的右邻居比较
if (arr[mid] < arr[mid + 1]) {
// 如果右邻居更大，说明正处于一个“上坡”
// 峰值必定在右半部分
// 因此，可以安全地抛弃左半部分（包括 mid）
l = mid + 1;
} else {
// arr[mid] >= arr[mid + 1]
// 如果右邻居更小或相等，说明正处于一个“下坡”或平台
// mid 本身可能就是一个峰值，或者峰值在它的左边
// 因此，峰值必定在左半部分（包括 mid）
r = mid; // 这里不写 r = mid - 1，因为 mid 可能就是那个峰值
}
}
return l; // 循环结束时，l 和 r 指向同一个位置，这个位置保证是一个峰值
}
void testAndPrint(const vector<int> &arr) {
printf("数组：[ ");
for (int x : arr) {
printf("%d ", x);
}
printf("]\n");
int peak_idx = findPeakElement(arr);
if (peak_idx == -1) {
printf("输入错误\n");
} else {
printf("找到一个峰值，索引为 %d 值为 %d\n", peak_idx, arr[peak_idx]);
}
}
int main()
{
// 测试用例 1：峰值在中间
testAndPrint({1, 3, 20, 4, 1, 0});
// 测试用例 2：峰值是最后一个元素
testAndPrint({1, 2, 3, 4, 5});
// 测试用例 3：峰值是第一个元素
testAndPrint({10, 9, 8, 7, 6});
// 测试用例 4：数组中有多个峰值
testAndPrint({1, 5, 2, 8, 3, 7, 4});
// 测试用例 5：只有两个元素
testAndPrint({1, 100});
return 0;
}
选择题：对数组进行二分查找的过程中，以下哪个条件必须满足？
- A. 数组必须是有序的
- B. 数组必须是无序的
- C. 数组长度必须是 2 的幂
- D. 数组中的元素必须是整数
答案
A
二分答案
二分思想不仅可以在有序序列中快速查询元素，还能高效率地解决一些具有单调性判定的问题。
回顾一下前面的二分查找：给定一个升序数组 \(a\)，想查找 \(\ge k\) 的第一个数在哪里。令“条件”为大于等于 \(k\)，则相当于找到最小的位置使得“条件”成立。假定答案在 \([L,R]\) 中，先检验区间中点 \(mid\)，如果“条件”不成立，说明答案一定在 \([mid+1,R]\) 中，否则一定在 \([L,mid]\) 里。
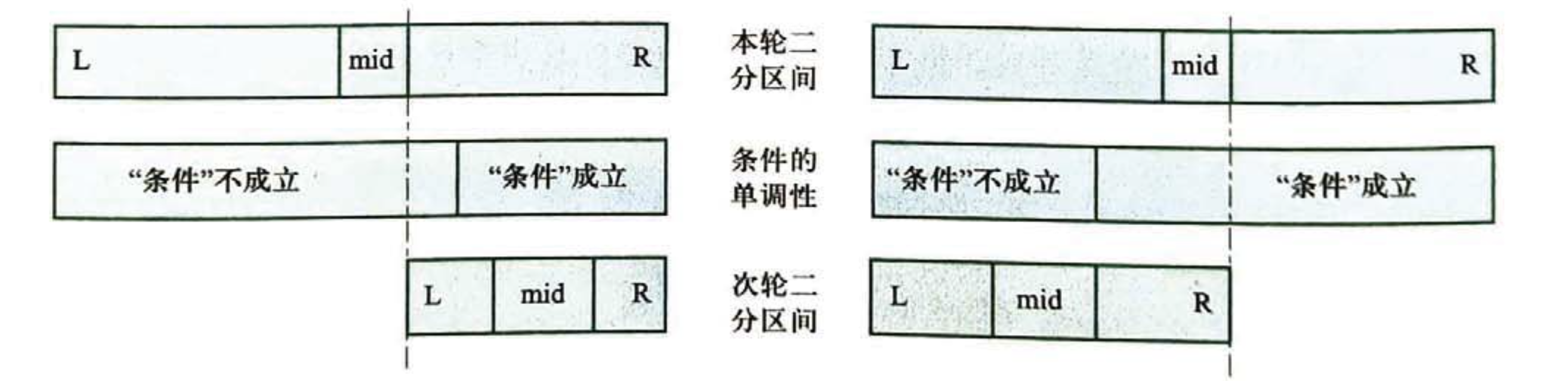
这实际上是单调性判定问题。
例题：P1824 进击的奶牛
一个牛棚有 \(n\) 个隔间，它们分布在一条直线上，坐标是 \(x_1,x_2,\cdots,x_n\)。现在需要把 \(c\) 头牛安置在指定的隔间，使得所有牛中相邻两头的最近距离越大越好，求这个最大的最近距离。例如，有 \(5\) 个隔间，\(3\) 头牛，隔间的坐标是 \([1,2,8,4,9]\)。可以将牛关在 \([1,4,9]\) 这些隔间中，最近的距离是 \(3\)。如果要求所有牛之间的距离都大于 \(3\)，则不存在这样的方案，因此最大的最近距离就是 \(3\)。
分析：如果这个最近间隔距离很小（考虑最近距离是 \(0\)），则不管要安排多少头牛都没有问题。随着最近间隔距离的增大，可以安排的牛的数量上限会越来越小（想象一下间距极大时相当于只能放 \(1\) 头牛）。因此本题相当于找一个最大的 \(x\)，使得刚好满足要求，如果再增大一个单位，就无法满足要求。这样的 \(x\) 就是答案。
可以从 \(0\) 开始一个单位一个单位往上枚举，每次枚举间距时都计算一下此时最多能安排多少头牛，如果间距为 \(x\) 时还能至少安排 \(c\) 头牛，但是间距为 \(x+1\) 时不够了，输出 \(x\)。这种方法答案肯定是对的，但是时间复杂度是 \(O(n \max \{ x_i \})\)，效率很低，因此需要考虑更好的办法。
令“条件”表示“当间隔距离至少为 \(x\) 时是否可以安排至少 \(c\) 头牛”，那么就是要找最大的 \(x\) 使得“条件”成立。当 \(x\) 超过某个数时，“条件”一定不成立，而不超过这个数时，“条件”一定成立。也就是说，这个“条件”具有单调性，因此符合二分的条件。
那么问题变为如何高效地检验“条件”的可行性。也就是限制任意两头安排的牛的距离不能小于 \(x\)，于是可以想到一种贪心算法：先在最左端安置一头牛，接下来从左往右依次遍历每个隔间，如果与上一个安置牛的隔间已经拉开足够的距离，就在此处放置一头牛，可以证明安置一定比不安置更优。最后只要看总共安置的牛的数量有没有超过 \(c\) 即可。
#include <cstdio>
#include <algorithm>
using std::sort;
const int N = 1e5 + 5;
int x[N], n, c;
bool check(int d) {
// 先在x[1]处安排一头牛
int cnt = 1, pre = x[1];
for (int i = 2; i <= n; i++) {
if (x[i] - pre >= d) { // 与上一头牛拉开足够间距，可以安排
cnt++; pre = x[i];
}
}
return cnt >= c; // 验证当前距离限制下是否可行（够安排c头牛）
}
int main()
{
scanf("%d%d", &n, &c);
for (int i = 1; i <= n; i++) scanf("%d", &x[i]);
sort(x + 1, x + n + 1); // 先将所有隔间位置排序
int l = 0, r = x[n] - x[1]; // 设置二分的起始区间
int ans; // 记录最后一次可行的最近距离
while (l <= r) {
int mid = (l + r) / 2;
if (check(mid)) { // 如果这个最近距离可行，尝试更大的情况
l = mid + 1; ans = mid;
} else { // 如果这个最近距离不可行，尝试更小的情况
r = mid - 1;
}
}
printf("%d\n", ans);
return 0;
}
例题：P1873 [COCI2011-2012#5] EKO / 砍树
有 \(n \ (n \le 10^6)\) 棵树，每棵树的高度分别为 \(a_1,a_2, \cdots, a_n\)，对于一个砍树高度 \(h\)，可以将每棵树上比 \(h\) 高的部分的木材锯下并收集起来（不高于 \(h\) 的部分保持不变），现在要求最大的整数高度 \(h\)，使得能够收集到长度至少为 \(m\) 的木材。
分析：如果锯子高度设得很低，可以收集到的木材会非常多，以至于超过需要的数量。随着砍树高度逐渐变大，获得的木材会逐渐减少。砍树高度增加到一定程度时，收集到的木材会开始变得不够。因此需要找到最大的 \(x\)，使得刚好满足要求；而哪怕再把高度调高 \(1\) 个单位，都无法满足要求。这样的 \(x\) 就是答案。
令“条件”表示“当砍树高度为 \(x\) 时是否可以获取至少 \(m\) 的木材”，那么就是要找最大的 \(x\) 使得“条件”成立。这个“条件”具有单调性：当 \(x\) 超过某个数时，“条件”一定不成立，而不超过这个数时，“条件”一定成立。因此可以二分。
证明了“条件”的单调性以后，问题就转化成了：如何判断“条件”是否成立，即当砍树高度为 \(x\) 时能否获得至少 \(m\) 的木材。 这只需要模拟题意计算即可。
#include <cstdio>
const int N = 1e6 + 5;
int a[N], n, m;
bool check(int h) { // 检验当砍树高度为h时，能否收集到至少m的木材
int s = 0;
for (int i = 1; i <= n; i++) {
if (a[i] > h) {
s += a[i] - h; // 按照题意模拟
if (s >= m) return true; // 收集够了则表示可行
}
}
return false;
}
int main()
{
scanf("%d%d", &n, &m);
int r = 0;
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
if (a[i] > r) r = a[i];
}
int l = 0; // 二分的左端点是0，右端点是最大的树高（答案不可能比最高的树还高）
int ans = 0;
while (l <= r) {
int mid = (l + r) / 2;
if (check(mid)) { // 如果check(mid)为真，说明mid是一个可行解，还可以尝试更高的砍树高度
l = mid + 1; ans = mid;
} else { // 如果check(mid)为假，应该尝试更低的砍树高度
r = mid - 1;
}
}
printf("%d\n", ans);
return 0;
}
这里每次 check 的时间复杂度为 \(O(n)\)，而二分答案本身的时间复杂度为 \(O(\log \max \{ a_i \})\)，因此总的时间复杂度为 \(O(n \log \max \{ a_i \})\)，可以在规定时间内得到答案。
使用二分答案的条件：
1.问题可以被归纳为找到使得某条件 \(P(x)\) 成立（或不成立）的最大（或最小）的 \(x\)。
2.把 \(P(x)\) 看作一个值为真或假的函数，那么它一定在某个分界线的一侧全为真，另一侧全为假。
3.可以找到一个高效的算法来检验 \(P(x)\) 的真假。
通俗地说，二分答案可以用来处理“最大的最小”或“最小的最大”类问题。
完善程序题
（序列合并）有两个长度为 \(N\) 的单调不降序列 \(A\) 和 \(B\)，序列的每个元素都是小于 \(10^9\) 的非负整数。在 \(A\) 和 \(B\) 中各取一个数相加可以得到 \(N^2\) 个和，求其中第 \(K\) 小的和。上述参数满足 \(N \le 10^5\) 和 \(1 \le K \le N^2\)。
#include <iostream>
using namespace std;
const int maxn = 100005;
int n;
long long k;
int a[maxn], b[maxn];
int* upper_bound(int *a, int *an, int ai) {
int l = 0, r = ___①___;
while (l < r) {
int mid = (l+r)>>1;
if (___②___) {
r = mid;
} else {
l = mid + 1;
}
}
return ___③___;
}
long long get_rank(int sum) {
long long rank = 0;
for (int i = 0; i < n; ++i) {
rank += upper_bound(b, b+n, sum - a[i]) - b;
}
return rank;
}
int solve() {
int l = 0, r = ___④___;
while (l < r) {
int mid = ((long long)l+r)>>1;
if (___⑤___) {
l = mid + 1;
} else {
r = mid;
}
}
return l;
}
int main() {
cin >> n >> k;
for (int i = 0; i < n; ++i) cin >> a[i];
for (int i = 0; i < n; ++i) cin >> b[i];
cout << solve() << endl;
}
- ①处应填？
- A.
an-a - B.
an-a-1 - C.
ai - D.
ai+1
- ②处应填？
- A.
a[mid] > ai - B.
a[mid] >= ai - C.
a[mid] < ai - D.
a[mid] <= ai
- ③处应填？
- A.
a+l - B.
a+l+1 - C.
a+l-1 - D.
an-l
- ④处应填？
- A.
a[n-1]+b[n-1] - B.
a[n]+b[n] - C.
2 * maxn - D.
maxn
- ⑤处应填？
- A.
get_rank(mid) < k - B.
get_rank(mid) <= k - C.
get_rank(mid) > k - D.
get_rank(mid) >= k
答案
代码分析
solve() 函数：这是一个典型的二分答案框架，它在所有可能的和的范围内（从 l 到 r）进行二分查找，对于一个猜测的和 mid，它需要判断这个 mid 在所有 n*n 个和中排名是太大还是太小。
get_rank(int sum) 函数：这个函数的作用是计算有多少个和 a[i] + b[j] 是小于等于 sum 的。它遍历数组 a 中的每一个元素 a[i]，它需要在数组 b 中找到有多少个 b[j] 满足 a[i] + b[j] <= sum，即 b[j] <= sum - a[i]。将对每个 a[i] 找到的 b[j] 的数量累加起来，就是 sum 的排名。
upper_bound(int *a, int *an, int ai) 函数：这是一个手写的 upper_bound 函数，get_rank 需要找到满足 b[j] <= sum - a[i] 的 b[j] 数量，这等价于在 b 数组中找到第一个大于 sum - a[i] 的元素的位置，这个位置的索引就是满足条件的 b[j] 的数量。所以，这个 upper_bound 函数的功能就是查找 b 数组中第一个大于 ai（这里的 ai 实际上是 sum - a[i]）的元素。
题目解答
-
A。
upper_bound函数的第二个参数an是指向数组末尾的下一个位置的指针，l和r代表索引，那么r应该是an - a。 -
A。要找第一个大于
ai的元素，在二分查找中，如果a[mid]大于ai，说明a[mid]以及它右边的所有元素都可能是要找的目标（或者比目标更大），所以可以安全地将搜索范围缩小到左半部分，即r = mid。如果a[mid]不大于ai（即小于等于），说明a[mid]以及它左边的所有元素都太小了，需要在右半部分继续查找，即l = mid + 1。 -
A。循环结束时，
l和r相遇，它们共同指向第一个大于ai的元素位置，所以函数应该返回指向这个位置的指针。 -
A。
solve函数在所有可能的和的范围内二分，r应该是可能的最大和，最大和就是a[n-1] + b[n-1]。 -
A。要找第
k小的和，get_rank(mid)计算的是小于等于mid的和的数量。如果get_rank(mid) < k，说明小于等于mid的和的数量还不够k个，这意味着第k小的和一定比mid大，所以应该在mid的右边继续查找，即l = mid + 1。如果get_rank(mid) >= k，说明小于等于mid的和的数量已经足够k个，mid本身可能是答案，或者答案比mid更小，所以应该在mid的左边（包括mid）继续查找，即r = mid。
例题：P1083 [NOIP2012 提高组] 借教室
分析：直接模拟题意很容易实现，从第一份订单开始处理每一份订单，针对每一个订单的时间区间，把每一天的剩余教室都减去相应的数量，如果某一次减完那一天剩余教室数变负数了，则可以提前结束并输出相应结果。这样做时间复杂度为 \(O(nm)\)，预期得分 \(30\) 分，实际上因为数据不够强提交后能获得 \(60\) 分。
参考代码
#include <cstdio>
const int N = 1e6 + 5;
int r[N];
int main()
{
int n, m; scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &r[i]);
}
int ans = 0;
for (int i = 1; i <= m; i++) {
int d, s, t; scanf("%d%d%d", &d, &s, &t);
bool flag = false;
for (int j = s; j <= t; j++) {
r[j] -= d;
if (r[j] < 0) {
flag = true; break;
}
}
if (flag) {
printf("-1\n"); ans = i; break;
}
}
printf("%d\n", ans);
return 0;
}
我们在前面学过，如果有多个区间操作进行叠加，可以用差分数组的思想来模拟。利用差分数组，我们可以把每一份订单的影响变成两次单点操作，但是如果我们要在订单完成后检验是否出现教室不够的现象依然需要对差分数组求一遍前缀和，这样总的时间复杂度还是 \(O(nm)\)。
注意到题目让我们求的是第一个会导致教室不够的订单，也就是说订单处理得越多，教室越容易不够。这样一来就具备了一种单调性，我们可以二分要处理前 \(x\) 个订单，从而检验这 \(x\) 个订单完成后某天的教室会不会不够。也就是说，如果我们把前 \(x\) 个订单都处理完之后发现教室不够，但前 \(x-1\) 个订单处理完时教室还够，则这个 \(x\) 就是要求的答案。二分第几个订单的时间复杂度为 \(O(\log m)\)，每次检验是否会导致教室不够的过程中利用差分数组可以将检验的复杂度做到 \(O(n+m)\)，因此整个算法的时间复杂度为 \(O((n+m) \log m)\)，符合题目的时间限制要求。
参考代码
#include <cstdio>
using ll = long long;
const int N = 1e6 + 5;
int r[N], d[N], s[N], t[N], n, m;
ll b[N]; // 差分数组
bool check(int x) { // 检验将前x份的订单完成后是否会出现教室不够的情况
for (int i = 1; i <= n + 1; i++) b[i] = 0; // 清空差分数组
for (int i = 1; i <= x; i++) {
b[s[i]] += d[i]; b[t[i] + 1] -= d[i]; // 差分思想模拟区间更新
}
for (int i = 1; i <= n; i++) {
b[i] += b[i - 1]; // 对差分数组求前缀和还原出原数组
if (b[i] > r[i]) return true;
}
return false;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &r[i]);
}
for (int i = 1; i <= m; i++) {
scanf("%d%d%d", &d[i], &s[i], &t[i]);
}
int ans = 0;
int l = 1, r = m;
while (l <= r) {
int mid = (l + r) / 2;
if (check(mid)) {
r = mid - 1; ans = mid;
} else {
l = mid + 1;
}
}
if (ans != 0) printf("-1\n");
printf("%d\n", ans);
return 0;
}
习题：P2440 木材加工
解题思路
每根小段木头越短，能切出来的总段数就越长，越能够满足 \(k\) 段的需求，每根小段木头越长，能切出来的总段数就越少，越难满足题目要求。因此可以对这个每段的长度进行二分，当每根小段木头的长度定下来时，总共能切出几根只需扫描一遍原木的长度即可。
特别地，如果每根原木的长度直接加起来都达不到 \(k\)（也就是每小段长度为 \(1\)），说明不可能满足要求，输出 \(0\)。
#include <cstdio>
#include <algorithm>
using std::max;
const int N = 1e5 + 5;
int a[N], n, k;
bool check(int x) {
int cnt = 0;
for (int i = 1; i <= n; i++) {
cnt += a[i] / x;
if (cnt >= k) return true;
}
return false;
}
int main()
{
scanf("%d%d", &n, &k);
int r = 1;
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]); r = max(r, a[i]);
}
int l = 1, ans = 0;
while (l <= r) {
int mid = (l + r) / 2;
if (check(mid)) {
l = mid + 1; ans = mid;
} else {
r = mid - 1;
}
}
printf("%d\n", ans);
return 0;
}
习题：P2678 [NOIP2015 提高组] 跳石头
解题思路
非常类似于 P1824 进击的奶牛，只不过那题是算出某种间距下最多可以安置多少头牛，这题是算出最少需要移走多少块石头。但是要注意的是，终点是独立于石头的一个单独的位置，需要把最后一跳也考虑进来。
#include <cstdio>
const int N = 5e4 + 5;
int d[N], L, n, m;
bool check(int dis) {
int cnt = 0; // 需要移除多少块石头
int pre = 0;
for (int i = 1; i <= n + 1; i++) { // 因为考虑终点，所以是n+1
if (d[i] - pre >= dis) { // 跳到下一块石头满足间距要求
pre = d[i];
} else { // 不满足间距要求，需要移除这块石头
cnt++;
if (cnt > m) return false; // 需要移除的石头超限了
}
}
return true;
}
int main()
{
scanf("%d%d%d", &L, &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", &d[i]);
}
d[n + 1] = L; // 注意最后还有一次跳到终点的过程
int l = 1, r = L, ans = 1;
while (l <= r) {
int mid = (l + r) / 2;
if (check(mid)) {
l = mid + 1; ans = mid;
} else {
r = mid - 1;
}
}
printf("%d\n", ans);
return 0;
}
习题：P1182 数列分段 Section II
解题思路
考虑两个极端情况，如果每个数自成一段，此时每段和最大值就是最大的那个数，如果总共只有一段，此时每段和最大值就是所有数加起来。这里我们可以得到一个单调性：对每段和设一个上限 \(x\)，如果 \(x\) 越小，需要分段的数量就越多，如果 \(x\) 越大，需要分段的数量就越少。而题目要我们求的实际上就是最小的一个 \(x\)，当每段和上限为 \(x\) 时，可以让分段数 \(\le m\)，而当每段和上限为 \(x-1\) 时，分段的段数只能 \(>m\)。这样的 \(x\) 就是我们要输出的结果，这个结果可以二分答案。这样问题就转化为了当我们限定分段和上限为 \(x\) 时，至少要分几段？
那么这个分段数的计算只需要从左往右依次处理即可，当累加和超出判断的上限时，做一次分段并从新的一段开始重新计算累加和，以此类推。
#include <cstdio>
#include <algorithm>
using std::max;
const int N = 1e5 + 5;
int a[N], n, m;
bool check(int x) { // 检验在分段和上限为x的情况下分段数是否可以<=m
int s = 0;
int cnt = 0; // 至少需要的分段数
for (int i = 1; i <= n; i++) {
if (s + a[i] <= x) {
s += a[i];
} else { // 在a[i-1]和a[i]之间划一刀
cnt++; s = a[i];
}
}
cnt++; // 不要忘了最后一段
return cnt <= m;
}
int main()
{
scanf("%d%d", &n, &m);
int l = 0, r = 1e9;
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
l = max(l, a[i]);
}
int ans = r;
while (l <= r) {
int mid = (l + r) / 2;
if (check(mid)) {
r = mid - 1; ans = mid;
} else {
l = mid + 1;
}
}
printf("%d\n", ans);
return 0;
}
习题：P8800 [蓝桥杯 2022 国 B] 卡牌
解题思路
显然要凑的套数越多越难凑，答案满足单调性性质，可以二分答案。
二分要凑的套数，如果某种牌的初始数量不够需要的套数，就用空白牌补充对应的数量，通过空白牌的消耗数量来判断能否凑出这么多套。注意二分答案的边界。
#include <cstdio>
#include <algorithm>
using ll = long long;
using std::max;
const int N = 2e5 + 5;
int a[N], b[N], n;
ll m;
bool check(int x) {
ll rest = m;
for (int i = 1; i <= n; i++) {
if (x - a[i] > b[i]) return false;
int need = max(x - a[i], 0);
rest -= need;
if (rest < 0) return false;
}
return true;
}
int main()
{
scanf("%d%lld", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= n; i++) scanf("%d", &b[i]);
int l = 0, r = n * 2, ans = 0; // 注意二分的边界，答案的最大情况是一开始已经有n套
// 额外的m张空白牌最多还能提供n套
while (l <= r) {
int mid = (l + r) / 2;
if (check(mid)) {
l = mid + 1; ans = mid;
} else {
r = mid - 1;
}
}
printf("%d\n", ans);
return 0;
}
例题：CF1486D Max Median
分析：二分答案 \(x\)，判断是否存在长度 \(\ge k\) 的连续子序列的中位数 \(\ge x\)。
如果一个区间的中位数 \(\ge x\)，那么其中 \(\ge x\) 的数的个数一定大于 \(\lt x\) 的数的个数。
将 \(\ge x\) 的数标记为 \(1\)，\(\lt x\) 的数标记为 \(-1\)，则当一个区间的标记和大于 \(0\) 时该区间中位数 \(\le x\)。
对于每一个区间右端点，可以找到长度 \(\le k\) 时左端点处的前缀和最小值，用右端点处前缀和与左端点处前缀和相减，如果 \(\gt 0\)，则存在相应区间，如果始终 \(\le 0\)，则不存在相应区间，整体的时间复杂度为 \(O(n \log n)\)。
参考代码
#include <cstdio>
#include <algorithm>
using std::sort;
using std::min;
const int N = 200005;
int n, k, a[N], tmp[N], pre[N];
bool check(int mid) {
for (int i = 1; i <= n; i++) {
if (a[i] < mid) {
tmp[i] = tmp[i - 1] - 1;
} else {
tmp[i] = tmp[i - 1] + 1;
}
pre[i] = min(pre[i - 1], tmp[i]);
}
for (int i = k; i <= n; i++)
if (tmp[i] - pre[i - k] > 0) return true;
return false;
}
int main()
{
scanf("%d%d", &n, &k);
for (int i = 1; i <= n; i++) {
scanf("%d", &a[i]);
}
int l = 1, r = n, ans = n;
while (l <= r) {
int mid = (l + r) / 2;
if (check(mid)) {
l = mid + 1; ans = mid;
} else {
r = mid - 1;
}
}
printf("%d\n", ans);
return 0;
}
习题：P1314 [NOIP2011 提高组] 聪明的质监员
解题思路
当 \(W=0\) 时，区间内的所有矿石都可以选上，\(W > \max \{ w_i \}\) 时，没有一个矿石选得上。可以发现，根据题目给的这个式子，\(W\) 越小，能够选到的矿石就越多，反之则越少。继而得到 \(W\) 越大，\(y\) 越小。题目要求我们最小化 \(|s-y|\)，实际上就是找离 \(s\) 最接近的 \(y\)。根据分析，我们可以二分答案 \(W\)，让其对应的 \(y\) 在 \(\ge s\) 和 \(<s\) 附近。
于是问题转化为当固定 \(W\) 时，如何高效地计算 \(y\)？可以利用前缀和来优化，显然当 \(w_i \ge W\) 时，这个矿石会算在区间检验值里，因此可以根据某一次的 \(W\) 制作出前 \(i\) 个矿石的有效个数前缀和以及前 \(i\) 个矿石的有效价值前缀和。再利用处理好的前缀和数组快速算出每个检验区间的检验值之和即可。
#include <cstdio>
#include <algorithm>
using std::max;
using std::min;
using ll = long long;
const int N = 2e5 + 5;
int sw[N], l[N], r[N], n, m, w[N], v[N];
ll sv[N];
ll calc(int W) { // 计算当设置参数为W时y的结果
for (int i = 1; i <= n; i++) { // 根据本次的W预处理两个前缀和
sw[i] = sw[i - 1] + (w[i] >= W);
sv[i] = sv[i - 1] + (w[i] >= W) * v[i];
}
ll res = 0;
for (int i = 1; i <= m; i++) {
// 利用前缀和快速求出每个检验区间的检验值
res += (sw[r[i]] - sw[l[i] - 1]) * (sv[r[i]] - sv[l[i] - 1]);
}
return res;
}
int main()
{
ll s; scanf("%d%d%lld", &n, &m, &s);
int L = 0, R = 0;
for (int i = 1; i <= n; i++) {
scanf("%d%d", &w[i], &v[i]);
R = max(R, w[i]);
}
R++; // 理论上当W等于最大的w+1时，检验值之和为0，因为此时一定选不出有效的矿石
for (int i = 1; i <= m; i++) {
scanf("%d%d", &l[i], &r[i]);
}
ll ans = s;
while (L <= R) {
int mid = (L + R) / 2;
ll tmp = calc(mid);
if (tmp >= s) {
L = mid + 1; ans = min(ans, tmp - s);
} else {
R = mid - 1; ans = min(ans, s - tmp);
}
}
printf("%lld\n", ans);
return 0;
}
例题：P3743 小鸟的设备
分析：对于这个问题而言，首先需要想到一个贪心策略：因为充电宝可以无缝切换地给任意一个设备充电，因此当某个设备电还没用完的时候是可以不管它的。于是就发现了问题的一个单调性：时间越短，需要充电的设备就越少，时间越长则需要充电的设备就越多。而充电能力是有限的，因此要找的是这样一个时间，在它之前充电宝足够让每个设备都有电，超过这个时间则会有某个设备开始没电。有这个单调性的存在，我们就可以对答案（使用时间）进行二分，那么问题就转化成了在指定时间内判定是否能让每个设备都有电。
根据每个设备的耗电速度 \(a_i\) 以及其初始电量 \(b_i\)，可以计算出该设备不充电情况下耗完电的时间，也就是 \(\frac{b_i}{a_i}\)，如果这个时间超过了当前判定的使用时间 \(t\)，则对其不需要充电；否则我们把这台设备每秒钟还差的电从充电宝的充电能力中拨出一部分给它，这部分需要的充电能力是 \(a_i - \frac{b_i}{t}\)。对于每个设备都按这个逻辑去计算即可得出在指定时间内能否保证每个设备都有电。
特别地，当充电宝的充电能力足够抵消每一个设备的耗电时，可以无限使用这些设备，输出 \(-1\)。
注意这是一个实数域上的二分答案问题，因此二分部分的代码框架与整数域略有不同。
#include <cstdio>
const int N = 1e5 + 5;
const double EPS = 1e-6;
int a[N], b[N], n, p;
bool check(double t) {
double rest = p;
for (int i = 1; i <= n; i++) {
double ti = 1.0 * b[i] / a[i]; // 注意a[i]和b[i]都是int类型
if (ti < t) {
rest -= (a[i] - b[i] / t);
// 注意double类型如何判断<0
if (rest < -EPS) return false; // 充电宝的充电能力不够分了
}
}
return true;
}
int main()
{
scanf("%d%d", &n, &p);
bool ok = true; // 假设能给所有设备都充电
int rest = p;
for (int i = 1; i <= n; i++) {
scanf("%d%d", &a[i], &b[i]);
if (ok && rest >= a[i]) {
rest -= a[i];
} else {
ok = false; // 说明不可能无限充电
}
}
if (ok) {
printf("-1\n");
} else {
// 注意右端点并不是1e5，而是要比1e10大一点
// 因为考虑 a[i]-b[i]/t 这个式子，如果a[i]很小，b[i]很大，则t可以达到1e10级别
double l = 0, r = 1e10 + 1;
while (r - l > EPS) { // 控制答案精度
double mid = (l + r) / 2;
if (check(mid)) {
l = mid;
} else {
r = mid;
}
}
printf("%.6f\n", l);
}
return 0;
}
二分的次数和精度有关，但是考虑每次二分的区间都可以缩小一半，缩减的速度还是很快的，因此也是对数级别。实数二分与整数二分有一些微妙的区别，需要确认好精度。比如本题答案的判定是基于误差不超过万分之一，因此我们可以将控制精度的量设到 1e-6 以确保精度足够但又不会计算过多。实际上，如果精度误差控制得过分小，反而可能会导致超时。
浙公网安备 33010602011771号