两个高斯分布乘积的理论推导
本文主要推导高斯分布(正态分布)的乘积,以便能更清楚的明白Kalman滤波的最后矫正公式。
Kalman滤波主要分为两大步骤:
1.系统状态转移估计;
2.系统测量矫正。
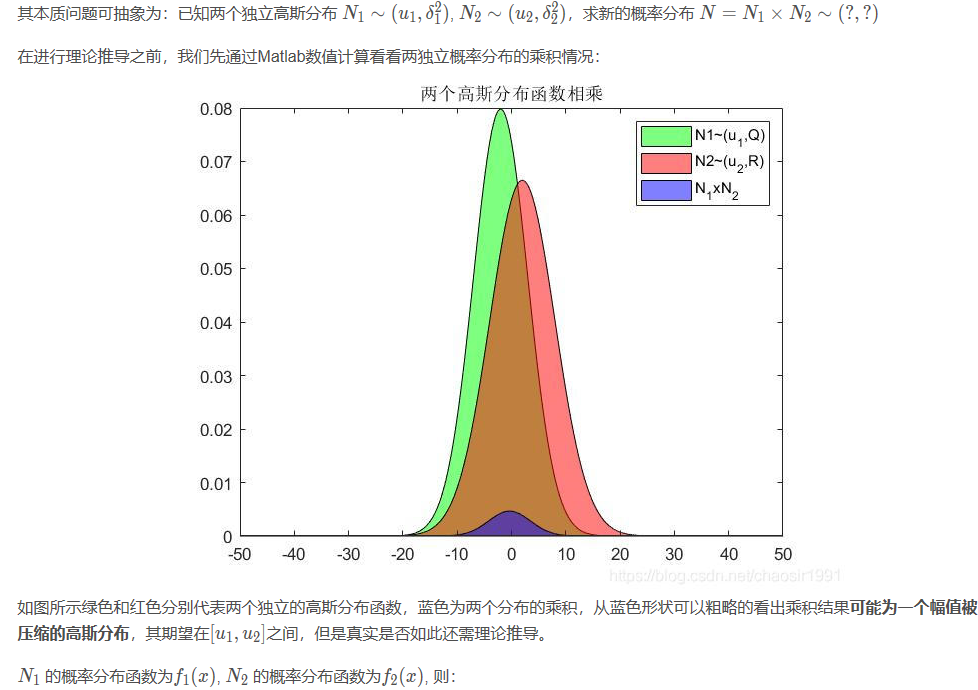
在第2步中的主要理论依据就是两个独立高斯分布的乘积如何计算的问题,即如何融合 估计值 和 观测值 得到系统状态的最优估计。
高斯分布的概率密度函数:
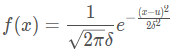




参考链接:两个高斯分布乘积的理论推导
其他文献:两个高斯函数的卷积仍为一高斯函数
本文主要推导高斯分布(正态分布)的乘积,以便能更清楚的明白Kalman滤波的最后矫正公式。
Kalman滤波主要分为两大步骤:
1.系统状态转移估计;
2.系统测量矫正。
在第2步中的主要理论依据就是两个独立高斯分布的乘积如何计算的问题,即如何融合 估计值 和 观测值 得到系统状态的最优估计。
高斯分布的概率密度函数:
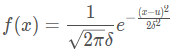







参考链接:两个高斯分布乘积的理论推导
其他文献:两个高斯函数的卷积仍为一高斯函数
