AC自动机

前置知识

Trie 树

Trie 树，又名字典树，以 \(0\) 节点根，每个节点对应一个字母（也有用边的），从根到某个节点的简单路径途径的字母为该节点表示的字符串。
下图以 i,hers,he,his,she 为字典构建字典树。

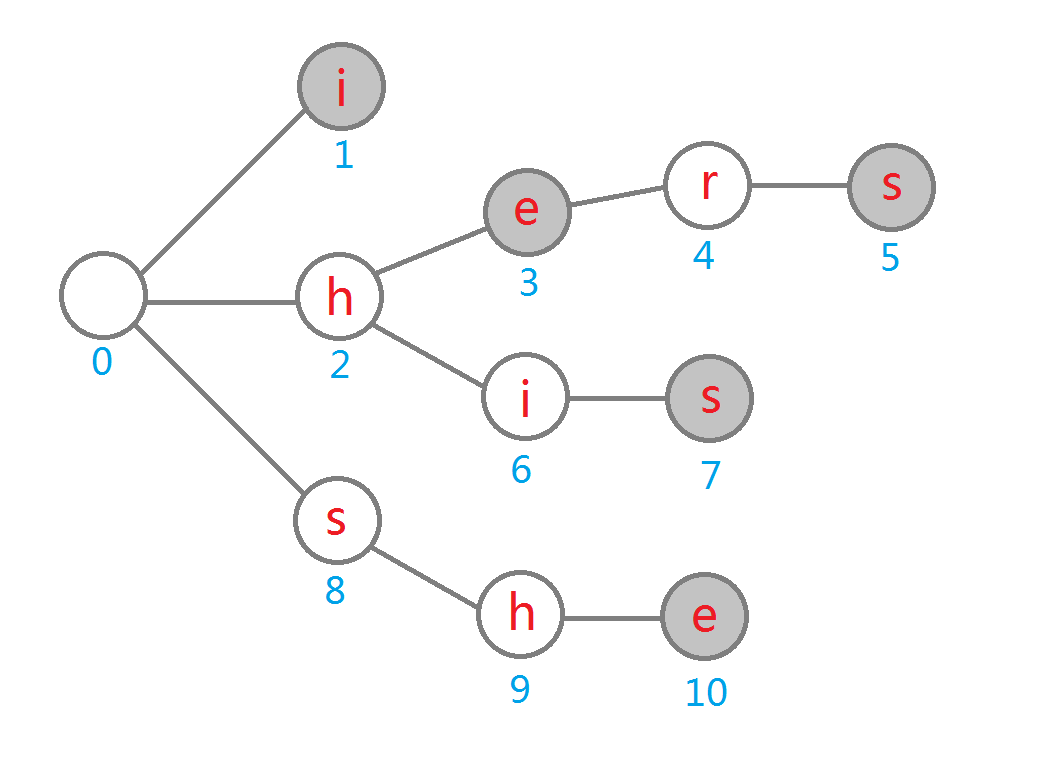
使用字典树可以快速查询与存储一系列字符串。

Knuth-Morris-Pratt 算法（KMP 算法）

\(KMP\) 算法的精髓在于对于字符串 \(s\)，构建失配指针 \(fail(next)\) 快速跳过匹配时的无用串，高效地执行查找任务。
一个字符串的某一个前缀的失配指针指向该前缀最大的相同真前后缀的位置，失配时可以跳转到该位置减少无用的匹配。

自动机

这部分其实可以不看
自动机，一般指 有限状态自动机，是 OI、计算机科学中被广泛使用的一个数学模型。

自动机是一个对信号序列进行判定的数学模型，即对一系列信号进行相应的判断的模型。自动机可以抽象为一张有向图，工作方式类似流程图，每一个节点是一个状态，一个判定节点，每条边可以接受多种字符。

形式地说，有限状态自动机（DFA）分为五部分：

1. 读入的字符集（\(\Sigma\)）；
2. 所有状态的集合状态集合（\(Q\)）；
3. 起始状态（\(s\in Q\)）；
4. 接受状态集合（\(F\subseteq Q\)）
5. 代表状态之间转移的转移函数（\(\delta\)），输入第一个状态与转移边的字符，返回得到的状态。

AC 自动机：例1 P3808【模板】AC 自动机（简单版）

给定 \(n\) 个模式串和一个文本串，输出在文本串中出现过的模式串的数量。

概念

AC 自动机（Aho-Corasick automaton）是基于KMP的思想建立起的一棵Trie 树。建立 AC 自动机的步骤为：

1. 建立 Trie 树：将所有模式串存入 Trie 树；
2. 建立 Fail 指针：对所有节点建立 Fail 指针。

变量声明

首先介绍以下的变量：

int n,t=0;
char s[maxn];
struct node{
	int fail,num;
	int son[30];
}a[maxn];

• n：模式串个数；
• t：节点数；
• s：模式串/文本串
• a：Trie 树：
• a.son：该节点的子节点；
• a.num：到该节点结束的字符串数量；
• a.fail:失配指针。

建 Trie 树

这部分和 Trie 模板一模一样，只是将模式串储存而已。

不断搜索每个模式串的每一位，建节点存储即可。

void insert(){
	int l=strlen(s+1),res=0;//以 0 为根，不断向下搜索
	for(int i=1;i<=l;i++){
		if(!a[res].son[s[i]-'a'+1]) a[res].son[s[i]-'a'+1]=++t;
                //若不存在这个子节点，则新建节点
		res=a[res].son[s[i]-'a'+1];//跳转
	}
	a[res].num++;//以 res 节点为结尾的字符串 +1
}

失配指针（重要）

AC 自动机中的失配指针其实有一点脱离了“失配”的限制。
在 AC 自动机中，fail 指针指向的是当前字符串的最长真后缀。这样可以让我们更好地搜索：

• 在失配时，我们可以跳转到该节点的最长真后缀继续匹配（因为要求哪些模式串在文本串出现过，所以只用统计后缀）；
• 而且，当我们搜索到一个节点时，我们可以利用该指针快速跳转到该词所有存在的后缀，以统计是否有后缀是所求的模式串。

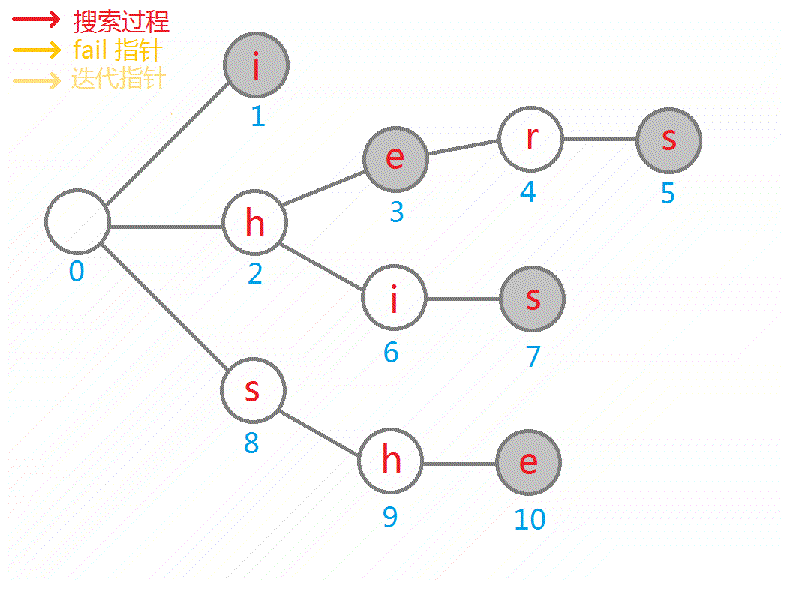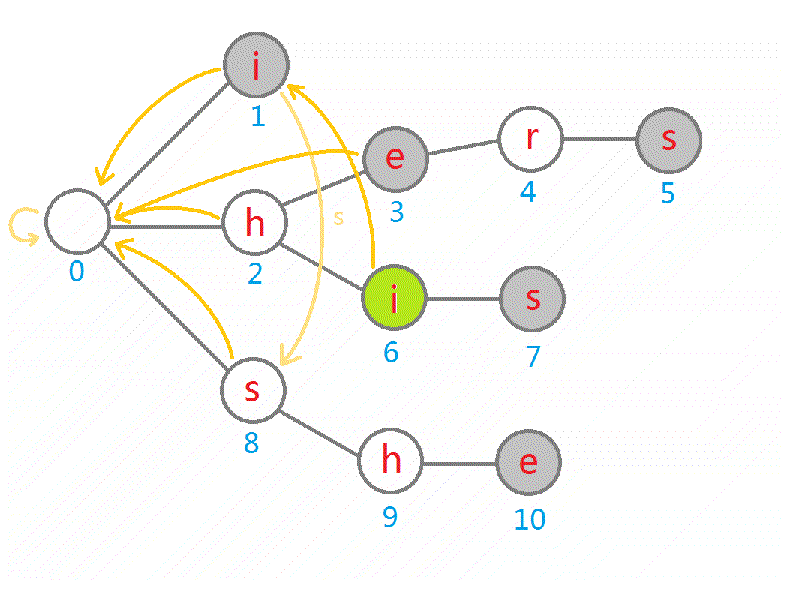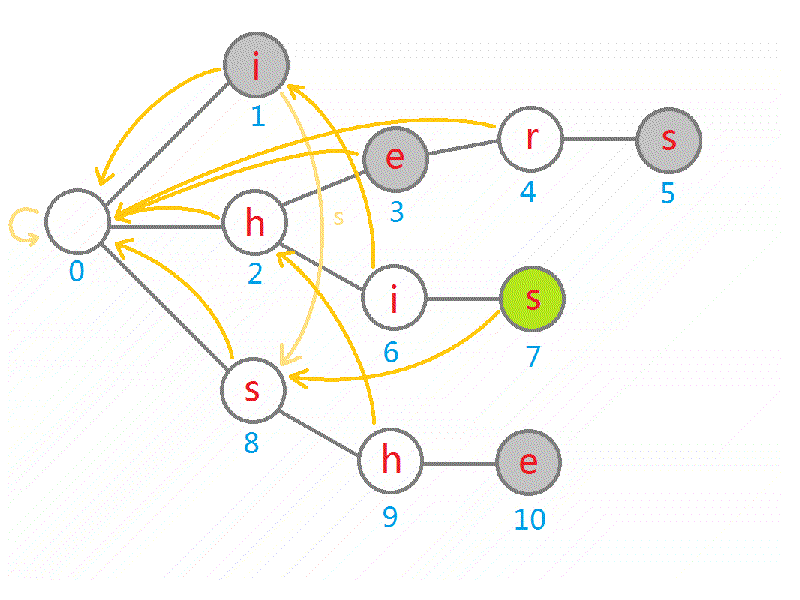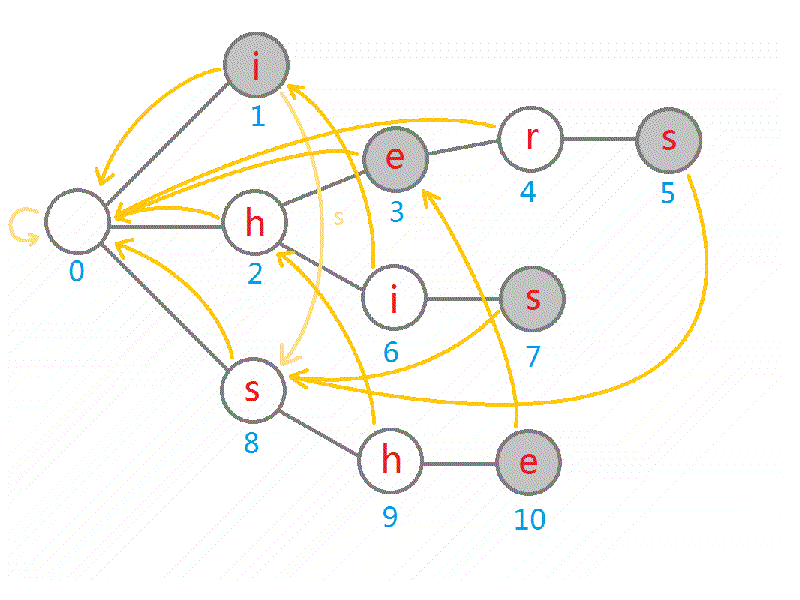
接下来讲如何求解 fail 指针：

• 我们可以 BFS 所有的顶点——这样可以保证当遍历到一个节点时，深度比它小的节点全部遍历过了，因为它的最长真后缀所在节点的深度一定小于它（要 BFS 的原因后面有写）；
• 对于每个节点 \(i\)，我们可以遍历它的所有子节点，对于第 \(x\) 个子节点（即通过字符 \(x\) 连接） \(i.son[x]\)：
• 假设节点 \(i.son[x]\) 存在，即我们建树的时候建过这个节点了，那么我们直接将 \(i.son[x]\) 的 fail 指针设为 \(fail_i\) 的第 \(x\) 个子节点即可。因为既然 \(fail_i\) 是最长真后缀的结尾了， \(fail_i.son[x]\) 一定就是 \(i.son[x]\) 的最长真后缀的结尾。那么要是 \(fail_i\) 的这个子节点不存在呢？这就启示我们进行优化了。
  
• 假设节点 \(s\) 不存在，那么，我们考虑刚刚的问题，假设 \(fail_i.son[x]\) 不存在，理论上我们应该再向前搜 \(fail_{fail[i]}.son[x]\) 直到存在或搜到根为止。我们可以优化这样的重复步骤：还记得之前我们是用 BFS 遍历的图吗？这就意味着，我们在处理 \(i\) 节点时已经处理好了深度更小的 \(fail_i,fail_{fail[i]},…\)，于是我们考虑，若没有这个子节点，直接将这个 \(i.son[x]\) 赋值为 \(fail_{fail[i]}.son[x]\)，这样我们赋值 \(fail_i.son[x]\) 时就可以直接令其等于 \(fail_i.son[x]\)，这样尽管其不存在，我们也提前设置了迭代的指针，减少了一遍遍跑 while 的时间。
  

queue<int> q;
void setfail(){
	int l=strlen(s+1);
	for(int i=1;i<=26;i++) if(a[0].son[i]) q.push(a[0].son[i]);
	while(!q.empty()){
		int top=q.front();q.pop();
		for(int i=1;i<=26;i++){
			if(a[top].son[i]){
				a[a[top].son[i]].fail=a[a[top].fail].son[i];
				q.push(a[top].son[i]);
			}else a[top].son[i]=a[a[top].fail].son[i];
		}
	}
}

关于为什么先遍历根节点将其所有子节点入队而不是直接将根入队，一是因为所有变量初始值为 0，没有大影响；更重要的是若将根先入队，则等到遍历根的子节点时，模拟能知道会直接将它们的 fail 指针指向自己而非根。

下面是完整的 gif：

查询