KMP
比如说,你想要在一篇文章中找到一个特定的字符串,显然,Ctrl+F即可。
那么,如何在代码中实现这个功能呢?
例1 P3375【模板】KMP字符串匹配
给定两字符串 \(s_1\) 和 \(s_2\),输出 \(s_2\) 在 \(s_1\) 中出现的所有位置及 border 数组(后面会讲)。
我们先令 \(|s_1|,|s_2|\) 为两字符串的长度且都以下标 \(1\) 开始。
先考虑第一个询问,显然,我们可以暴力枚举 \(s_1\) 的每一位作为 \(s_2\) 的第一位,之后枚举 \(|s_2|\) 的每一位比较。这样的复杂度是 \(\mathcal{O}(|s_1\|s_2|)\) 的(应该是吧),我们考虑是否有更加简单的方法。
假设 \(s_1=AAAAAAAAAB,s_2=AAB\),那么,我们看一看模拟的过程就能发现:
第一次匹配 \(s_1\) 的前三位,在最后一位时不匹配;
\(A\ A\ \color{red}A\ A\ A\ A\ A\ A\ A\ B\)
\(A\ A\ \color{red}B\)
第二次匹配二到四位,在最后一位时不匹配;
\(A\ A\ A\ \color{red}A\ A\ A\ A\ A\ A\ B\)
\(\quad A\ A\ \color{red}B\)
……
我们发现,每次都是在最后一位时不匹配(即失配),这将复杂度大大提升了。而在观察后我们知道,既然在最后一位失配了,那么说明在前几位中两字符串一定是匹配的。这提示我们可以直接跳过某些位置,而直接从后面可能的位置开始匹配。
假设 \(s_1=ABCABABCABC,s_2=ABCABC\)。
首先我们在 \(s_1\) 的第一位开始匹配:
\(A\ B\ C\ \color{green}{\underline{A\ B}}\ \color{red}{A}\ A\ B\ C\ A\ B\ C\)
\(\color{green}{\underline{A\ B}}\ C\ A\ B\ \color{red}{C}\)
在失配时,我们发现,前 \(5\) 位都是匹配的,且为 \(ABCAB\),所以我们下一次是不是可以不从 \(s_1\) 的第二位,而是用这五位中开头和最后都有的 \(\color{green}{\underline{AB}}\) 来快速跳过中间不可能成功的字符,也就是直接快进到:
\(A\ B\ C\ \color{green}{\underline{A\ B}}\ A\ A\ B\ C\ A\ B\ C\)
\(\quad\quad\quad\color{green}{\underline{A\ B}}\ C\ A\ B\ C\)
我们可以再举一个例子,假设 \(s_1=AAAAABAAAB,s_2=AAAAB\)。先从 \(s_1\) 的第一位开始匹配:
\(A\ \color{green}{\underline{A\ A\ A}}\ \color{red}{A}\ B\ A\ A\ A\ B\)
\(\color{green}{\underline{A\ A\ A}}\ A\ \color{red}B\)
此时在第 \(5\) 位失配,我们发现前 \(4\) 位 \(AAAA\) 中都存在 \(\color{green}{\underline{AAA}}\),于是我们快进到这两处重合时继续匹配:
\(A\ \color{green}{\underline{A\ A\ A}}\ A\ B\ A\ A\ A\ B\)
\(\quad\color{green}{\underline{A\ A\ A}}\ A\ B\)
有人可能会问:第二组例子为什么选的一定是 \(AAA\) 而不是 \(A\) 和 \(AA\) 之类的,显然这两个都位于匹配成功的串的开头和结尾,能够帮助我们快速向后跳转,甚至跳转地更多,为什么不选他们呢?
其实很简单,我们假设使用 \(\color{green}{\underline{AA}}\) 作为我们选择的串,那么就会跳转到:
\(A\ [A\ \color{green}{\underline{A\ A}}\ A\ B\,]\ A\ A\ A\ B\)
\(\quad\quad\;\color{green}{\underline{A\ A}}\ A\ A\ \;B\)
显然我们漏了一组解,这就是跳转太快的后果。
所以我们每次失配时,我们都要选择一个子串,使得它既是失配位置前子串(即匹配成功的部分)的真前缀(即前缀,但是不等于整个串)又是真后缀(这样才能快速跳转),而且要长度最大(确保不漏解)。我们发现开始时就能枚举好这些子串,而这就是 KMP 中最重要的 \(next\) 数组(即题中 border 数组)。
next 数组
\(next_i\) 表示在 \(i\) 位置失配时,我们应该将 \(s_2\) 后移几位继续下一次匹配,即 \(s_2[1]\sim s_2[i-1]\) 中最长的相等的真前缀与真后缀的长度(注意不一定非得是 \(s_2[1]\sim s_2[i-1]\),根据题目我们也可以改成 \(s_2[1]\sim s_2[i]\) 的)。所以我们的 \(next\) 数组是对 \(s_2\) 求解的。
显然,\(next_1=0\),因为在 \(1\) 位置前没有字符;\(next_2=0\),因为在 \(2\) 之前的子串为 \(s_2[1]\),不存在真前缀和真后缀。
而 \(i\ge 3\) 时,我们考虑如何求解 \(next_i\)。
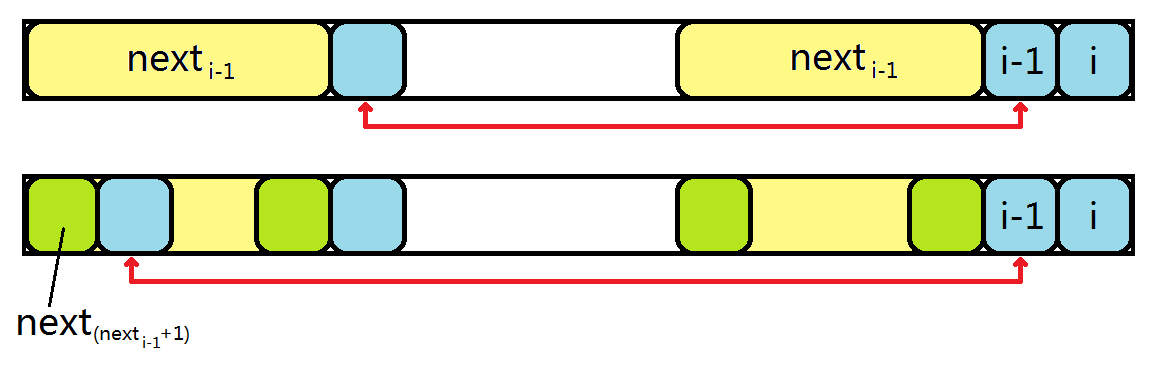
假设我们已经求解出了 \(next_{1\sim i-1}\),那么,我想求 \(next_i\),就相当于是求 \(s_2[1]\sim s_2[i-1]\) 的最长相等的真前、后缀的长度。而我们已经知道 \(s_2[1]\sim s_2[i-2]\) 的这个值了(即为 \(next_{i-1}\)),所以我们发现,如果 \(s_2[next_{i-1}+1]=s_2[i-1]\) 的话(上图中红色箭头指向的一对),因为 \(s_2[1]\sim s_2[next_{i-1}]\) 和 \(s_2[(i-1)-next_{i-1}]\sim s_2[i-2]\) 正好相等(上图中淡黄色部分),所以 \(s_2[1]\sim s_2[next_{i-1}+1]\) 和 \(s_2[(i-1)-next_{i-1}]\sim s_2[i-1]\) 就相等,而这就是我们想要求的 \(next_i\) 了。
但是若 \(s_2[next_{i-1}+1]=s_2[i-1]\) 的话,我们不妨再看 \(s_2[1]\sim s_2[next_{i-1}]\) 的最长相等的真前、后缀,即 \(next_{(next[i-1]+1)}\)(下图中浅绿色部分),由于两淡黄色部分一样,故两部分的首位都是浅绿的那一部分。所以,若 \(s_2[next_{(next[i-1]+1)}+1]=s_2[i-1]\) 的话(下图中淡黄色部分),\(s_2[1]\sim s_2[next_{(next[i-1]+1)}+1]\) 就是我们所要的一段。
若还不是,同理,我们继续找浅绿色段的 \(next\),直到找到或搜完,若搜完了还没找到则无解。
我们举个例子理解一下。
初始时:
\(\quad s_2:A\ B\ C\ A\ B\ B\ A\ B\ C\ A\ B\ C\)
\(next:\,0\ \ 0\ \ 0\ \ 0\ \ 1\ \ 2\ \ 0\ \ 1\ \ 2\ \ 3\ \ 4\ \ 5\ \ \color{red}{?}\)
假设我们要求 \(next_{13}\),即整个串中最长的相等的真前缀与真后缀的长度,根据我们所说,先比较 \(s_2[next_{i-1}+1]\) 和 \(s_2[i-1]\)(蓝色字符):
\(\quad s_2:\color{green}{\underline{A\ B\ C\ A\ B}}\ \color{blue}{B}\ \color{green}{\underline{A\ B\ C\ A\ B}}\ \color{blue}{C}\)
\(next:\,0\ \ 0\ \ 0\ \ 0\ \ 1\ \ 2\ \ 0\ \ 1\ \ 2\ \ 3\ \ 4\ \ \color{green}{5}\ \ \color{red}{?}\)
若它们相等,那么答案就是 \(6\),因为 \(s_2[1]\sim s_2[6]\) 和 \(s_2[7]\sim s_2[12]\) 就相等了。但是不相等,那么,我们再找 \(next[next_{i-1}+1]\) 即 \(next_6 = 2\):
\(\quad s_2:\color{green}{\underline{\color{orange}{A\ B}\ \color{blue}{C}\ \color{orange}{A\ B}}}\ B\ \color{green}{\underline{\color{orange}{A\ B}\ C\ \color{orange}{A\ B}}}\ \color{blue}{C}\)
\(next:\,0\ \ 0\ \ 0\ \ 0\ \ 1\ \ \color{green}{2}\ \ 0\ \ 1\ \ 2\ \ 3\ \ 4\ \ 5\ \ \color{red}{?}\)
此时我们发现 \(s_2[next_6+1]=s_2[i-1]\),发现相等,那么我们的答案就是 \(next_6+1=3\):
\(\quad s_2:\color{green}{\underline{A\ B\ C}}\ A\ B\ B\ A\ B\ C\ \color{green}{\underline{A\ B\ C}}\)
\(next:\,0\ \ 0\ \ 0\ \ 0\ \ 1\ \ 2\ \ 0\ \ 1\ \ 2\ \ 3\ \ 4\ \ 5\ \ \color{red}{3}\)
对于题中第二个询问,即 border 数组的输出,我们只需要输出 \(next_2\sim next_{|s_2|+1}\) 即可(后移一位是因为我们的 \(next_i\) 存 \(s_2[1]\sim s_2[i-1]\) 的答案)。
主体部分
在求解了 \(next\) 之后,我们进行答案的求解。
我们先设两个变量 \(i,j\) 分别进行 \(s_1\) 和 \(s_2\) 的匹配。
首先,我们令 \(s_1=s_2=1\),并逐位向后进行配对。等到失配时,我们就将 \(j\) 往回倒到 \(next_{j}+1\) 进行下一次匹配。特殊地,若 \(j=1\) 说明第一位就失配了,直接将 \(i++\) 即可。
若判断到有 \(s_2\) 包含在 \(s_1\) 时,输出答案后,我们要将 \(s_2\) 再向前移到下一个位置继续匹配,此时我们可以看作是在下一位失配了,将 \(i++,j=next_{j+1}+1\) 即可。
直到 \(i\) 匹配完时结束程序。
- 举一个例子:
(以红色代表 \(i,j\) 正在匹配的位置,绿色+下划线代表匹配成功的位置,其中的橙色字符代表匹配成功的串的最长相等的真前后缀,再其中橙色下划线的代表下一次移位对齐的部分)
\(\quad s_1 = \color{red}{A}\ B\ A\ A\ A\ B\ A\ A\ B\ A\ A\ B\ A\ A\ A\ B\)
\(\quad s_2 = \color{red}{A}\ B\ A\ A\ B\)
\(next =\,0\ \ 0\ \ 0\ \ 1\ \ 1\ \ 2\) - 首先逐位匹配,到 \(i=j=5\) 时失配:
\(\quad s_1 = \color{green}{\underline{\color{orange}{A}\ B\ A\ }\color{orange}{\underline{A}}}\ \color{red}{A}\ B\ A\ A\ B\ A\ A\ B\ A\ A\ A\ B\)
\(\quad s_2 = \color{green}{\color{orange}{\underline{A}}\underline{\ B\ A\ \color{orange}{A}}}\ \color{red}{B}\)
\(next =\,0\ \ 0\ \ 0\ \ 1\ \ \color{red}{1}\ \ 2\) - 将 \(j\) 跳转到 \(next_j+1\),为了方便我们将 \(i,j\) 对齐:
\(\quad s_1 = A\ B\ A\ \color{green}{\underline{A}}\ \color{red}{A}\ B\ A\ A\ B\ A\ A\ B\ A\ A\ A\ B\)
\(\quad s_2 = \qquad\quad \color{green}{\underline{A}}\ \color{red}{B}\ A\ A\ B\)
\(next =\,\qquad\quad 0\ \ 0\ \ 0\ \ 1\ \ 1\ \ 2\) - 再次逐位向后匹配,在 \(j=2\) 时失配:
\(\quad s_1 = A\ B\ A\ \color{green}{\underline{A}}\ \color{red}{A}\ B\ A\ A\ B\ A\ A\ B\ A\ A\ A\ B\)
\(\quad s_2 = \qquad\quad \color{green}{\underline{A}}\ \color{red}{B}\ A\ A\ B\)
\(next =\,\qquad\quad 0\ \ \color{red}{0}\ \ 0\ \ 1\ \ 1\ \ 2\) - 由于此时 \(next_j = 0\),将 \(j\) 跳转至 \(0+1 = 1\):
\(\quad s_1 = A\ B\ A\ A\ \color{red}{A}\ B\ A\ A\ B\ A\ A\ B\ A\ A\ A\ B\)
\(\quad s_2 = \qquad\qquad \color{red}{A}\ B\ A\ A\ B\)
\(next =\,\qquad\qquad 0\ \ 0\ \ 0\ \ 1\ \ 1\ \ 2\) - 再次逐位匹配到 \(j=5=|s_2|\),说明匹配成功了,输出答案,并将 \(i++,j=next_{j+1}+1\)(看作下一位失配)(防止颜色重叠此时 \(i,j\) 往前移了一位,就是看做这里失配了):
\(\quad s_1 = A\ B\ A\ A\ \color{green}{\underline{\color{orange}{A\ B}\ A\ }\color{orange}{\underline{A\ B}}}\ \color{red}{A}\ A\ B\ A\ A\ A\ B\)
\(\quad s_2 = \qquad\qquad \color{green}{\color{orange}{\underline{A\ B}}\underline{\ A\ \color{orange}{A\ B}}}\ \color{red}{\,\_}\)
\(next =\,\qquad\qquad 0\ \ 0\ \ 0\ \ 1\ \ 1\ \ \color{red}{2}\) - 此时 \(j=3\):
\(\quad s_1 = A\ B\ A\ A\ A\ B\ A\ \color{green}{\underline{A\ B}}\ \color{red}{A}\ A\ B\ A\ A\ A\ B\)
\(\quad s_2 = \qquad\qquad\qquad\quad \color{green}{\underline{A\ B}}\ \color{red}{A}\ A\ B\)
\(next =\,\qquad\qquad\qquad\quad 0\ \ 0\ \ 0\ \ 1\ \ 1\ \ 2\) - 再次逐位匹配到最后发现再次匹配成功,输出答案,重复操作:
\(\quad s_1 = A\ B\ A\ A\ A\ B\ A\ \color{green}{\underline{\color{orange}{A\ B}\ A\ }\color{orange}{\underline{A\ B}}}\ \color{red}{A}\ A\ A\ B\)
\(\quad s_2 = \qquad\qquad\qquad\quad \color{green}{\color{orange}{\underline{A\ B}}\underline{\ A\ \color{orange}{A\ B}}}\ \color{red}{\,\_}\)
\(next =\,\qquad\qquad\qquad\quad 0\ \ 0\ \ 0\ \ 1\ \ 1\ \ \color{red}{2}\) - \(j\) 移位后:
\(\quad s_1 = A\ B\ A\ A\ A\ B\ A\ A\ B\ A\ \color{green}{\underline{A\ B}}\ \color{red}{A}\ A\ A\ B\)
\(\quad s_2 = \qquad\qquad\qquad\qquad\qquad \color{green}{\underline{A\ B}}\ \color{red}{A}\ A\ B\)
\(next =\,\qquad\qquad\qquad\qquad\qquad 0\ \ 0\ \ 0\ \ 1\ \ 1\ \ 2\) - 逐位匹配,\(j=5\) 时失配:
\(\quad s_1 = A\ B\ A\ A\ A\ B\ A\ A\ B\ A\ \color{green}{\underline{\color{orange}{A}\ B\ A\ }}\color{orange}{\underline{A}}\ \color{red}{A}\ B\)
\(\quad s_2 = \qquad\qquad\qquad\qquad\qquad \color{orange}{\underline{A}}\color{green}{\underline{\ B\ A\ \color{orange}{A}}}\ \color{red}{B}\)
\(next =\,\qquad\qquad\qquad\qquad\qquad 0\ \ 0\ \ 0\ \ 1\ \ \color{red}{1}\ \ 2\) - 跳转 \(j\):
\(\quad s_1 = A\ B\ A\ A\ A\ B\ A\ A\ B\ A\ A\ B\ A\ \color{red}{A}\ A\ B\)
\(\quad s_2 = \qquad\qquad\qquad\qquad\qquad\qquad\quad \color{red}{A}\ B\ A\ A\ B\)
\(next =\,\qquad\qquad\qquad\qquad\qquad\qquad\quad 0\ \ 0\ \ 0\ \ 1\ \ 1\ \ 2\) - 向后跳转匹配,发现 \(i\) 出界了,结束。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#define maxn 1000005
#define next nnext
using namespace std;
char a[maxn],b[maxn];
int next[maxn];
int main(){
cin>>a+1>>b+1;int la=strlen(a+1),lb=strlen(b+1);
//求解 next
next[1]=0;next[2]=0;
for(int i=3;i<=lb+1;i++){
int j=next[i-1];
while(j>=1&&b[j+1]!=b[i-1]) j=next[j+1];
if(b[j+1]==b[i-1]) j++; next[i]=j;
}
// for(int i=1;i<=strlen(b+1);i++) printf("%c ",b[i]);printf("\n");
// for(int i=1;i<=strlen(b+1)+1;i++) printf("%d ",next[i]);
//求解答案
for(int i=1,j=1;i<=la;){
if(a[i]!=b[j]){
if(j==1) {i++;continue;}
j=next[j]+1;
continue;
}
if(j==lb){printf("%d\n",i-lb+1);i++;j=next[j+1]+1;continue;}
i++;j++;
}
for(int i=2;i<=lb+1;i++) printf("%d ",next[i]);
return 0;
}
/*
ABAAABAABAABAAAB
ABAAB
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号