牛顿法，拟牛顿法，及与梯度下降法的比较

1. 牛顿法求方程的根

假设我们需求$f(x)=0$的根，并假设$f(x)=0$可导。首先，把$f(x)$在$x_0$进行一阶泰勒展开：

由$f(x)=0$可得：

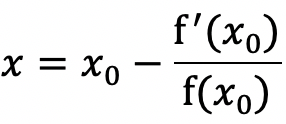
因此迭代公式为：

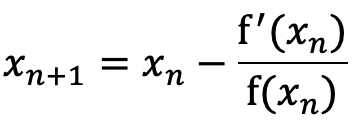
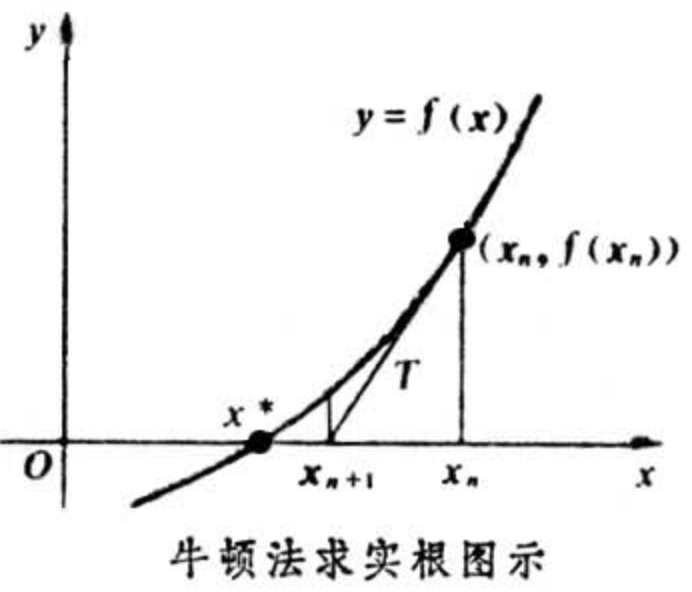
2. 牛顿法求极小值

 

 

 

 

 

6. 牛顿法和梯度下降法的比较

这里我们用一个简单的例子比较牛顿法和梯度下降法的收敛效果：求$f(x)=x^4$的极小值。实现代码如下：

 

import numpy as np
import matplotlib.pyplot as plt


# 目标函数:y=x^4
def func(x):
    return x**4


# 目标函数一阶导数:dy/dx=2*x
def dfunc(x):
    return 4 * x**3


# 目标函数二阶导数
def ddfunc(x):
    return 12 * x**2


# Newton method
def newton(x_start, epochs):
    """
    牛顿迭代法。给定起始点与目标函数的一阶导函数和二阶导数，求在epochs次迭代中x的更新值
    :param x_start: x的起始点
    :param epochs: 迭代周期
    :return: x在每次迭代后的位置（包括起始点），长度为epochs+1
    """
    xs = np.zeros(epochs+1)
    x = x_start
    xs[0] = x
    for i in range(epochs):
        delta_x = -(dfunc(x)/ddfunc(x))
        x += delta_x
        xs[i+1] = x
    return xs


# Gradient Descent
def GD(x_start, epochs, lr):
    """
    梯度下降法。给定起始点与目标函数的一阶导函数，求在epochs次迭代中x的更新值
    :param x_start: x的起始点
    :param epochs: 迭代周期
    :param lr: 学习率
    :return: x在每次迭代后的位置（包括起始点），长度为epochs+1
    """
    xs = np.zeros(epochs+1)
    x = x_start
    xs[0] = x
    for i in range(epochs):
        dx = dfunc(x)
        # v表示x要改变的幅度
        v = - dx * lr
        x += v
        xs[i+1] = x
    return xs


line_x = np.linspace(-1, 1, 100)
line_y = func(line_x)

x_start_newton = -1
x_start_GD = 1
epochs = 6

lr = 0.08
x_newton = newton(x_start_newton, epochs)
x_GD = GD(x_start_GD, epochs, lr=lr)

plt.plot(line_x, line_y, c='r')

color_newton = 'g'
plt.plot(x_newton, func(x_newton), c=color_newton, label='Newton')
plt.scatter(x_newton, func(x_newton), c=color_newton, )

color_GD = 'b'
plt.plot(x_GD, func(x_GD), c=color_GD, label='Grad Decent')
plt.scatter(x_GD, func(x_GD), c=color_GD, )

plt.legend()
plt.show()

结果如下，梯度下降算法的收敛效果受学习率影响：

 

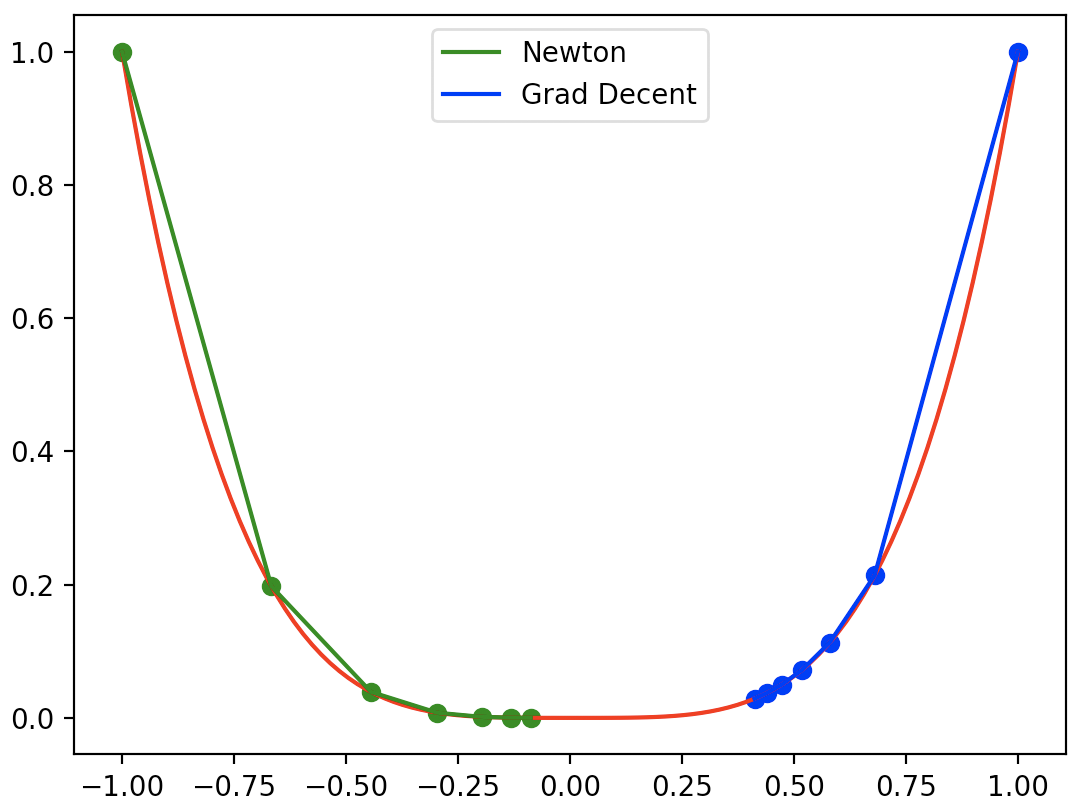
梯度下降法和牛顿法的比较：（摘自博客：牛顿法优缺点）

梯度下降法利利用目标函数的一阶偏导数信息、以负梯度方向作为搜索方向。

牛顿法不仅使用目标函数的一阶偏导数，还进一步利⽤了目标函数的二阶偏导数，这样就考虑了梯度变化的趋势，因⽽而能更全面地确定合适的搜索⽅方向加快收敛，它具二阶收敛速度。

但牛顿法主要存在以下两个缺点：

1. 对目标函数有较严格的要求。函数必须具有连续的一、二阶偏导数，海海森矩阵必须正定。
2. 计算相当复杂，除需要计算梯度以外，还需要计算二阶偏导数矩阵和它的逆矩阵。计算量、存储量均很⼤，且均以维数N的平⽅增加，当N很⼤时这个问题更加突出。

⽜顿法虽然收敛速度快，但是计算过程中需要计算目标函数的二阶偏导数，计算复杂度较⼤。而且有时目标函数的海森矩阵无法保持正定，从而使⽜顿法失效。为了克服这两个问题，⼈们提出了拟⽜牛顿法。这个方法的基本思想是：不⽤⼆阶偏导数而构造出可以近似海森矩阵或者海森矩阵的逆的正定对称阵，在拟⽜顿的条件下优化⽬目标函数。不同的构造⽅法就产生了不同的拟牛顿法。也有人把“拟牛顿法”翻译成“准牛顿法”，其实都是表示“类似于牛顿法”的意思，因此只是对算法中用来计算搜索方向的海森矩阵（或海森矩阵的逆）作了近似计算罢了。