LCA的离线快速求法（Tarjan）
最常见的LCA（树上公共祖先）都是在线算法，往往带了一个log。有一种办法是转化为“+-1最值问题”得到O(n)+O(1)的复杂度，但是原理复杂，常数大。今天介绍一种允许离线时接近线性求LCA的Tarjan算法。
一个点和其他点的LCA必定是它到root路径上的所有节点之一，而另一个节点刚好在哪个节点下，LCA就是谁：
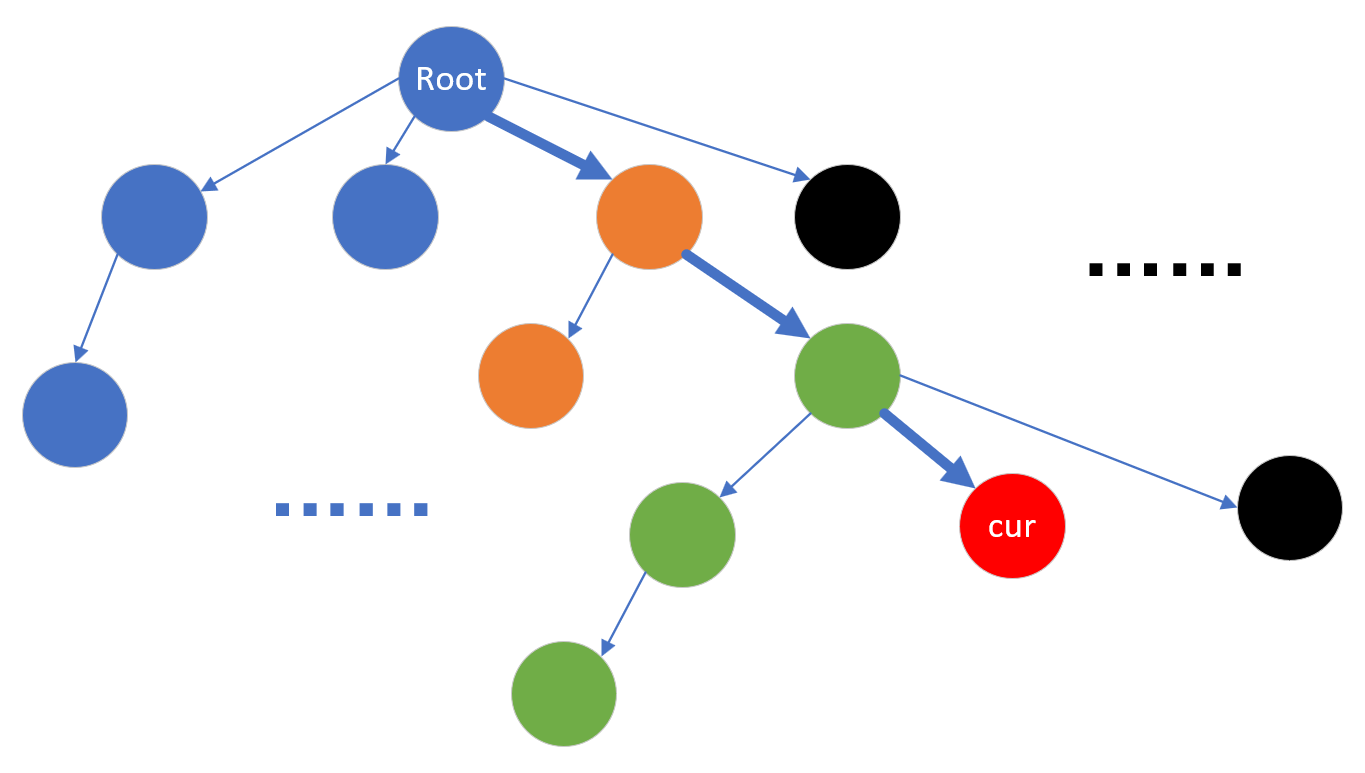
如图，标粗的箭头为当前搜索的路径，左边为已经搜索完毕的路径，右边的黑色节点尚未搜索。现在要求节点cur和节点a的LCA，显然a是什么颜色，LCA就也是这个颜色，如果a还没有被搜索到，那就不处理，把这个询问留给搜索到a的时候处理（那个时候cur肯定已经访问过了）。
那怎么做这个染色呢？我们对所有节点做一个并查集，每当一个节点搜索完毕，处理完了自己的答案，就把自己合并到父亲fa里面，那么在我搜完之后，父节点fa搜完之前，fa的其他所有儿子的公共祖先都是fa了：
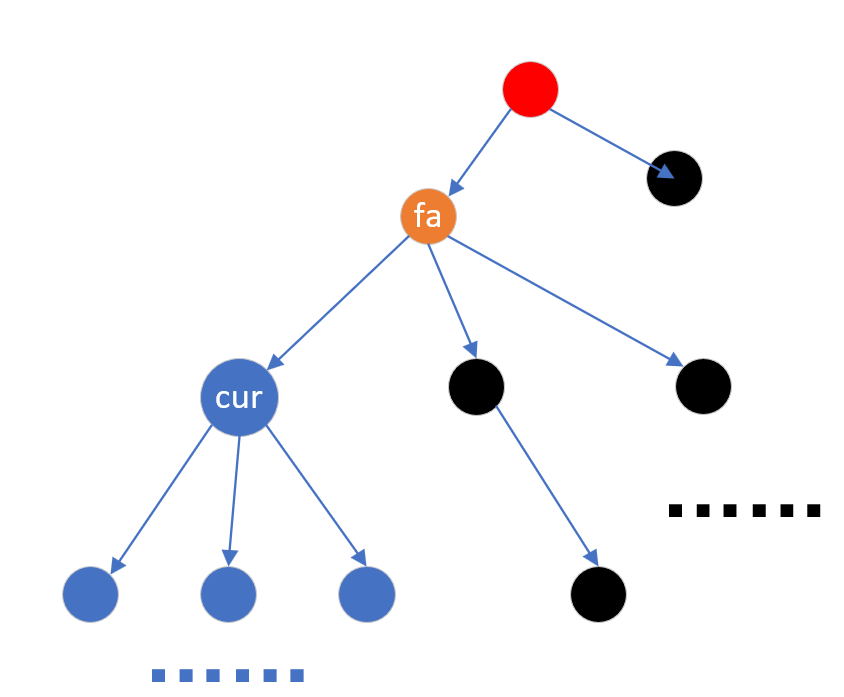
当cur节点搜索完毕后，回到fa，讲cur修改为橙色并入到fa里（而且我们使用了并查集，此后查询cur的子节点也将得到fa），之后在fa搜索其他儿子节点时，他们和cur子树里的节点的LCA一定是fa，而当fa全部搜索完成后，他又被并入上级节点，以此类推，就可以在一遍dfs中就获取所有询问的答案。
参考代码：
int N, Q, p[MAX], qa[MAX], qb[MAX], ans[MAX];
vector<int> has[MAX];
struct ufs {
int in[MAX];
ufs() {
std::iota(in, in + N, 0);
}
void merge(int v, int u) { //! v合并给u
in[v] = u;
}
int find(int u) {
return in[u]==u ? u : (in[u] = find(in[u])); //! 带路径压缩
}
};
class Tree
{
std::vector<int> son[MAX];
ufs f;
void getans(int u) {
for (auto v: son[u]) {
getans(v); f.merge(v, u); //! 处理子树后，将其并入
}
for (auto i: has[u]) {
auto v (qa[i]^qb[i]^u); //! 该询问的另一个点
if (f.find(v) != v) ans[i] = f.find(v);
}
}
public:
#define root 0
Tree() {
for (int i = 1; i < N; ++i) son[p[i]].push_back(i);
getans(root);
}
#undef root
};
main() {
scanf("%d%d", &N, &Q);
for (int i = 1; i < N; ++i) scanf("%d", p + i);
for (int i = 0; i < Q; ++i) {
scanf("%d%d", qa + i, qb + i);
has[qa[i]].push_back(i);//! 把询问归到qa和qb下
has[qb[i]].push_back(i);
}
auto tr = new Tree;
for (int i = 0; i < Q; ++i)
printf("%d\n", ans[i]);
}
