常见排序算法
快速排序
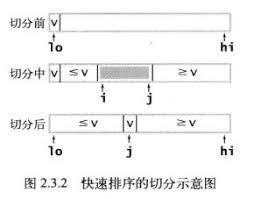 

快排是不稳定的排序算法, 如随机选择 pivot, partition 时相同的大小的值可能互换
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
步骤为:
- 从数列中挑出一个元素,称为"基准"(pivot),
- 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任何一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursively)把小于基准值元素的子数列和大于基准值元素的子数列排序。
- 递归到最底部时,数列的大小是 0 或 1,也就是已经排序好了。
这个算法一定会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
解法 1
#include <iostream>
#include <vector>
using namespace std;
void quickSort(vector<int>& nums, int start, int end) {
if (end - start <= 0) {
return;
}
// // 随机算法只是多两行
// // 0 ≤ rand()%(right - start + 1) <= end-start, 故加 1
// // start <=start + rand()%(right - start) <= end
int random_index = start + std::rand()%(end - start + 1);
std::swap(nums[end], nums[random_index]);
int pivot = nums[end];
int left = start;
int right = end;
while (left <= right) {
while (left <= right && nums[left] < pivot) {
++left;
}
while (right >= left && nums[right] >= pivot) {
--right;
}
// 当left = right + 1时,数组是有序的,不需要交换; 只有当left < right 时才需要交换
if (left < right) {
std::swap(nums[left++], nums[right--]);
}
}
std::swap(nums[left], nums[end]);
quickSort(nums, start, left - 1);
quickSort(nums, left + 1, end);
}
int main() {
vector<int> nums;
srand(47);
for (int i = 0; i < 10; i++) {
int e = rand() % 20;
nums.push_back(e);
cout << e <<'\t';
}
cout << endl;
quickSort(nums, 0, nums.size() - 1);
for (int e : nums) {
cout << e <<'\t';
}
return 0;
}
解法 2
#include <iostream>
#include <vector>
using namespace std;
int partition(vector<int>& vec, int left, int right) {
// 随机算法最简单的使用方法就是随机一个位置, 然后和最后一个元素对调, 然后走正常路线
int pivot_idx = left + rand()%(right - left + 1);
swap(vec[pivot_idx], vec[right]);
// 上面两行是比正常路线多的代码
int pivot = vec[right];
int cursor = left;
for (int i = left; i < right; i++) {
if (vec[i] < pivot) {
swap(vec[i], vec[cursor++]);
}
}
swap(vec[right], vec[cursor]);
return cursor;
}
void quickSort(vector<int>& vec, int left, int right) {
if (left >= right) {
return;
}
int middle = partition(vec, left, right);
quickSort(vec, left, middle-1);
quickSort(vec, middle+1, right);
}
int main() {
vector<int> vec;
srand(47);
for (int i = 0; i < 10; i++) {
vec.push_back(rand() % 20);
}
for (int e : vec) {
cout << e <<'\t';
}
quickSort(vec, 0, vec.size()-1);
cout << endl;
for (int e : vec) {
cout << e <<'\t';
}
return 0;
}
链表的快速排序
leetcode 148.
Sort List: Sort a linked list in O(n log n) time using constant space complexity.
解法 1
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (!head) return nullptr;
int pivot = head->val;
ListNode small(0), large(0);
ListNode *pSmall = &small, *pMid = head, *pLarge = &large;
for (ListNode* cur = head->next; cur; cur = cur->next) {
if (cur->val == pivot) {
pMid->next=cur;
pMid=pMid->next;
} else if (cur->val < pivot) {
pSmall->next=cur;
pSmall=pSmall->next;
} else {
pLarge->next=cur;
pLarge=pLarge->next;
}
}
pSmall->next = nullptr;
pLarge->next = nullptr;
pMid->next = nullptr;
small.next = sortList(small.next);
pSmall = &small;
// 这是为了找前半部分的尾巴, 很关键
while (pSmall->next) {
pSmall=pSmall->next;
}
pSmall->next=head;
pMid->next=sortList(large.next);
return small.next;
}
};
解法 2
#include<iostream>
#include<vector>
using namespace std;
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
struct FrontEndNode {
ListNode* front;
ListNode* end;
FrontEndNode():front(nullptr), end(nullptr) {}
FrontEndNode(ListNode* front_, ListNode* end_):front(front_), end(end_) {}
};
class Solution {
public:
ListNode* sortList(ListNode* head) {
return quick_sort(head).front;
}
FrontEndNode quick_sort(ListNode *head) {
FrontEndNode ans(head, head);
// 1. 链表为空链表, 不用处理, 返回 (nullptr, nullptr)
// 2. 链表只有一个节点, 不用处理, 返回 (font=head, end=head)
if (!head || !head->next) return ans;
ListNode* pHead = head;
ListNode small(0), middle(0), large(0);
ListNode* pSmall = &small;
ListNode* pMiddle = &middle;
ListNode* pLarge = &large;
int pivot = head->val;
while (pHead) {
if (pHead->val < pivot) {
pSmall->next = pHead;
pSmall = pSmall->next;
} else if (pHead->val > pivot) {
pLarge->next = pHead;
pLarge = pLarge->next;
} else {
pMiddle->next = pHead;
pMiddle = pMiddle->next;
}
pHead = pHead->next;
}
pSmall->next = nullptr;
pMiddle->next = nullptr;
pLarge->next = nullptr;
FrontEndNode low = quick_sort(small.next);
FrontEndNode high = quick_sort(large.next);
// 假设前半段和后半段都为空
ans.front = middle.next;
ans.end = pMiddle;
// 拼接前半段和中间段
if (low.front) {
ans.front = low.front;
low.end->next = middle.next;
}
// 拼接中间段和后半段
if (high.front) {
pMiddle->next = high.front;
ans.end = high.end;
}
return ans;
}
};
归并排序
 

算法思路:
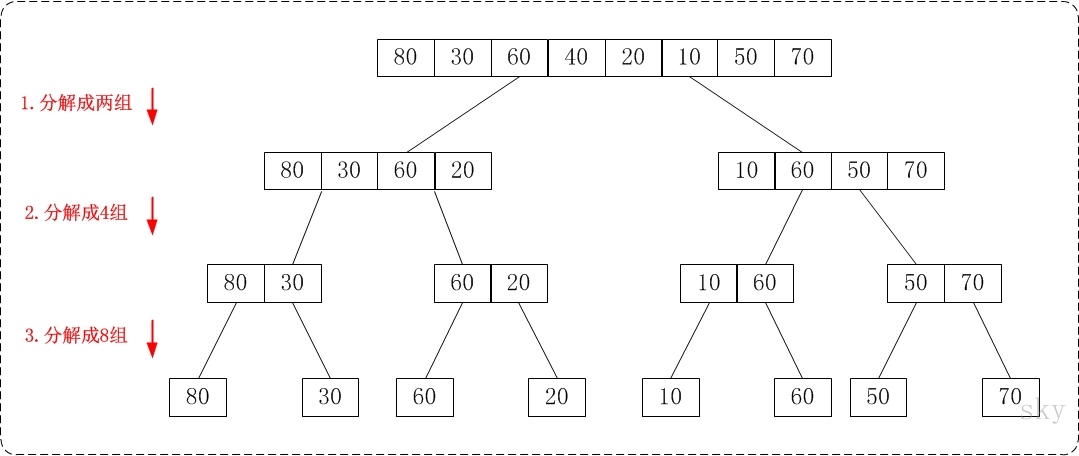
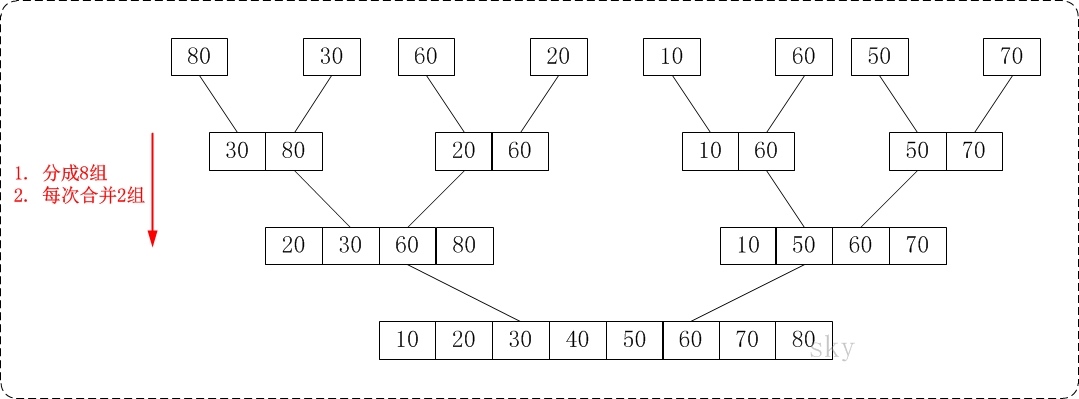
- 把 n 个记录看成 n 个长度为 1 的有序子表
- 进行两两归并使记录关键字有序,得到 n/2 个长度为 2 的有序子表
- 重复第 2 步直到所有记录归并成一个长度为 n 的有序表为止。
归并: 将两个已排序文档合并成一个更大的已排序文件的过程;
归并排序的性质:
- 归并排序对输入初始次序不敏感, 时间复杂度是 O(nlgn);
- 归并排序是稳定的排序算法;
- 归并排序不是原址排序(数组归并排序需要辅助数组, 空间复杂度 O(n), 链表的归并排序空间复杂度是 O(1));
- 归并排序适用于链表排序(leetcode 148);


解法 1
#include <iostream>
#include <vector>
using namespace std;
void merge(vector<int>& nums, int start, int middle, int end) {
int i = start;
int j = middle;
int k = 0;
vector<int> temp(end-start);
while (i < middle && j < end) {
if (nums[i] < nums[j]) {
temp[k++] = nums[i++];
} else {
temp[k++] = nums[j++];
}
}
int m = end - 1;
int n = middle - 1;
while (i++ < middle) {
nums[m--] = nums[n--];
}
for (int l = 0; l < k; l++) {
nums[start+l] = temp[l];
}
}
void merge_sort(vector<int>& nums, int start, int end) {
if (end-start <= 1) {
return;
}
int middle = (start+end) >> 1;
merge_sort(nums, start, middle);
merge_sort(nums, middle, end);
merge(nums, start, middle, end);
}
void merge_sort(vector<int>& nums) {
merge_sort(nums, 0, nums.size());
}
int main() {
int N;
while (cin >> N) {
vector<int> nums(N);
for (int i = 0; i < N; i++) {
nums[i] = rand()%50;
}
merge_sort(nums);
bool is_sorted = true;
int pre = INT_MIN;
for (auto&e : nums) {
cout << e << " ";
if (e < pre) is_sorted = false;
pre = e;
}
cout << endl << "sorted =>" << boolalpha<< is_sorted << endl;
}
}
链表的归并排序
leetcode 148. Sort List: Sort a linked list in O(n log n) time using constant space complexity.
Example 1:
Input: 4->2->1->3
Output: 1->2->3->4
Example 2:
Input: -1->5->3->4->0
Output: -1->0->3->4->5
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* sortList(ListNode* head) {
if (!head || !head->next) return head;
ListNode* slow = head;
ListNode* fast = head->next; // slow 输在起跑线上!
while (fast != nullptr && fast->next != nullptr) {
// 当链表长度为偶数时, slow 走一半,
// 当链表长度是奇数时, slow 位置为链表中点的前一个位置
slow = slow->next;
fast = fast->next->next;
}
ListNode* lhs = head;
ListNode* rhs = slow->next;
// 这个很重要
slow->next = nullptr;
// 这个很重要
lhs = sortList(lhs);
rhs = sortList(rhs);
return merge(lhs, rhs);
}
ListNode* merge(ListNode* l1, ListNode* l2) {
ListNode head(-1);
ListNode* p = &head;
while (l1 && l2) {
if (l1->val < l2->val) {
p->next = l1;
l1 = l1->next;
} else {
p->next = l2;
l2 = l2->next;
}
p = p->next;
}
if (l1) p->next = l1;
if (l2) p->next = l2;
return head.next;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号