nowgood

2024年4月20日

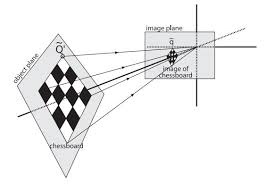
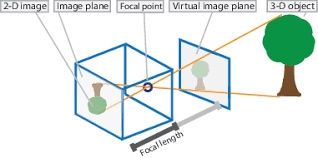
摘要：如何将图片上的像素坐标(u, v)投影到世界坐标系中, 即得到 $(x_w, y_w, z_w)$. 数学表达如下 \[\begin{align*} s\begin{bmatrix} u\\v\\1 \end{bmatrix} &= \begin{bmatrix} f_x & 0 & c_x & 阅读全文

posted @ 2024-04-20 22:11 nowgood 阅读(46) 评论(0) 推荐(0) 编辑

变换矩阵的理解

摘要：用于表示同一世界在不同坐标系下的坐标值为了方便理解, 建议先看线性代数的本质--基变换旋转矩阵这里变换矩阵, 为了方便, 我们先只考虑旋转 $R^{imu}_{global}$ 的列向量是imu坐标系的基向量在global坐标系下的坐标表示, 将imu坐标系下的坐标与R相乘, 得到同一个阅读全文

posted @ 2024-04-20 21:26 nowgood 阅读(24) 评论(0) 推荐(0) 编辑

2024年4月16日

配置ZSH， TMUX， VIM

摘要： Linux 神器 sudo apt-get install silversearcher-ag tree htop zsh git git-core autojump openssh-server vim curl hddtemp lm-sensors -y ZSH sh -c "$(curl -f 阅读全文

posted @ 2024-04-16 23:34 nowgood 阅读(25) 评论(0) 推荐(0) 编辑

2020年3月8日

已知路面同一位置不同高度2点, 获取此两点坐标

摘要：