知识性总结

1.Burnside&Pólya

概括

Burnside引理与Pólya计数定理常用于解决某种要求本质不同的计数问题，此处本质不同可能指旋转同构、翻转同构、树/图同构等等。有时候，这种问题无法直接组合计数或者 DP 计数，这个时候就可以考虑套用Burnside引理与Pólya计数定理。其中，Burnside引理的形式是这样的。

\(|X/G|=\frac{1}{|G|}\sum\limits_{g\in G}|X^g|\)。

这些概念基本上都是群论的概念，所以理解起来比较难。我只能说一下我的理解：造出这个问题的置换群，那么答案就是对于每一种置换而言，算出有多少种状态在这次置换后状态不变，求和再除以群的大小。可以发现这个算不动点数量的过程在没有特殊限制时是可以优化的。具体地说，一个置换中同一个小环只能涂一种颜色，所以总涂色方案数就是 \(m^{c(g)}\)，其中 \(m\) 是颜色数，\(c(g)\) 是置换 \(g\) 中小环的数量。因此，Pólya计数定理就这样被表述为：

\(|C^X/G|=\frac{1}{|G|}\sum\limits_{g\in G}m^{c(g)}\)。

综上，我认为Burnside引理与Pólya计数定理的题可以拆分成以下几个步骤。

• 找出基本置换并构造/搜索出置换群。
• 对单个置换进行组合计数/DP计数。
• (化简式子后)计算所有置换的答案并套用Burnside引理与Pólya计数定理。

题目

张阿姨玩魔方

题意：一个 \(3\times 3 \times 3\) 的正方体，用 \(k\) 种颜色分别给 \(54\) 个面，\(12\) 条棱和 \(8\) 个顶点染色，求旋转同构时本质不同的染色方案数。

普通的几何体旋转同构计数题。

使用画图3D分别写出点、线、面的基本置换，将其合在一起，并深搜出整个置换群（大小为 \(24\)。）需要注意的是，几何体只需要两个方向的基本置换就能深搜出整个置换群。并且一定要仔细，不然很难调。然后颜色没有特殊限制，套用Pólya计数定理就做完了。

[SHOI2006] 有色图

题意：一张图，用 \(k\) 种颜色给边染色，定义图 \(A\) 与图 \(B\) 同构当且仅当可以重排 \(A\) 中点的编号使两张图完全相同。求这种图同构时本质不同的染色方案数。

更像能在考场上遇到的Burnside引理题。（确实是在考场遇到的。）
依照之前写出的步骤，寻找置换群。发现群的大小很大，就是阶乘。但是又发现，这题对颜色没有什么特殊要求，所以可以考虑Pólya计数定理。由于知道Pólya计数定理只和小环（轮换）数量相关，那么定义置换 \(A\) 和置换 \(B\) 同构，当且仅当它们的所有轮换大小构成的多重集完全相同。在这种定义下，不同构的置换数量就只有 自然数分解种。在 \(n=53\) 的数据下搜索，发现自然数分解方案可以接受。

然后只需要对于每一种置换等价类，统计出它的大小和其中边的轮换数就行了。注意，这里是边的轮换数，刚刚统计的是点的置换等价类，因为这道题是在对点置换，对边染色，但又因为这张图是完全图，所以边的轮换数相对好求。

2.矩阵树定理

概括

矩阵树定理（Matrix-Tree），解决一类生成树计数问题。它的推广很多，值得拿出来一说的有 BEST 定理，用来求一张有向欧拉图的欧拉回路数量。矩阵树定理及其推广的证明与行列式相关，相对于群论较好理解，但是想自己写出来依旧困难。所以就只能说一说流程了：构造出原图的 Laplace 矩阵，然后删掉某行某列跑行列式即为答案。

其中，图 \(G\) 的 Laplace 矩阵形如这样（求以点 \(u\) 为根的内向生成树个数，想求外向生成树时将每条边反转过来再求内向生成树即可）：

\(L(G)=A(G)-Deg^{out}(G)\)。

\(A(G)\) 即为图 \(G\) 的邻接矩阵。\(Deg^{out}(G)\) 是图 \(G\) 的出度矩阵，当 \(i=j\) 时，\(Deg^{out}_{i,j} = deg^{out}(i)\)，否则 \(Deg^{out}_{i,j} = 0\)。

答案就是 \(L(G)\) 删去第 \(u\) 行第 \(u\) 列后的行列式的值。

虽然写证明有点困难，但是做题流程还是可以大体归纳的：

• 分析原问题，构造出生成树计数模型，找到需要对什么计数（生成树个数、边权和，边权和 \(k\) 次方的和等等）。
• 研究如何用乘法计算出该信息。
• 套用 Matrix-Tree 定理。

题目

Mirror Box

网格图，染色。仔细分析发现把格子看成点不好做，那么把格点看成点。把格点染成黑白相间的，容易发现当黑点全连通或白点全连通时满足条件。又因为不确定的边数 \(\leq 200\)，所以可以并查集缩点后跑两遍矩阵树。为什么这样是对的，是容易发现的呢？考虑对于黑点连通成树进行讨论。若成环，显然不符合条件。若边界上的点不连通，那么不符合条件 \(1\)。若边界上的点连通，但其与中间的点不连通，那么白点在分界处成环，不符合条件。白点连通成树的情况同理。

16 Integers

如果把每个四元组建成一个点，总共 \(16\) 个点的话，需要做的是统计每个点恰被经过若干次的欧拉路径的数量。这是不好做的。但可以发现，把每种可能的前 \(3\) 位建成一个点，总共 \(8\) 个点的话，每条边就能看成放置一个新四元组，这样就能正常地做统计每条边被经过若干次的欧拉路径的数量了。套用 BEST 定理即可。

3.拉格朗日插值

概括

理论上来说，拉格朗日插值应该归类于多项式全家桶里，但是呢以它为考点的题目很多，而且它的应用也较为广泛，且它容易理解，代码简单，最重要的是它不是10级知识点。拉插的做题流程也比较简单，大致概括如下：

• 写出小数据的普通 DP/组合计数。
• 发现答案是多项式，并且次数可以接受。
• 拉插。

其中最困难的一步一般是发现答案是多项式。

事实上，拉插大多数时候只是配菜。

题目

最大值求和

将 \(a\) 数组排序后枚举最大值。发现最大值 \(v\) 被 \(a\) 数组分成了 \(O(n)\) 个区间，每个区间的计数是大致相同的。假设现在区间为 \([l,r]\)，并且 \(a_k\) 到 \(a_n\) 都 \(\geq l\)，那么最大值为 \(v_0\) 时的权值就是 \(v_0 \times (v_0^{n-k+1}-(v_0-1)^{n-k+1})\times \prod\limits_{i=1}^{k-1} a_i\)。发现这个式子是多项式，那么它的前缀和也是多项式，那么就可以 \(O(n)\) 拉插求出 \(v_0\) 的取值在 \([l,r]\) 里时这个式子的值的和。总复杂度 \(O(n^2)\)。

发现很多拉插题我还没有补，之后再写。

4.虚树

概括

这是一个被降级的原10级知识点，现在一下砍到了8级。虚树本身并不难，无论是哪种建树方法都达不到10级。两种建树方法各有各优点，二次排序比较直接，但有的时候用不了，比如只知道 \(dep\) 的时候。有时候新的关键点和别的点的 LCA 求不了，也只能用单调栈建树。

直接考虚树的题会比较简单，但是虚树还是比较灵活的，在 SAM 的 Parent 上建虚树也不是什么新颖的东西。总之，虚树题大致分为两类，做题流程也有点不同。

第一类是树的点非常多，但是形态特殊，并且答案只和 \(n\) 个关键点有关，这个时候就可以建虚树，并且还要想想如何求两两关键点之间的 DFN 和 LCA。（关键点一般也有特殊性质，并且这种题一般只能用单调栈建树。）

第二类就是常见的树上多次询问，流程比较简单：

• 想出 \(O(n)\) 的树形 DP 或别的做法。
• 尝试将问题变得只和关键点有关。
• 使用虚树，做到 \(O(\sum k)\) 的复杂度。

建树方法也最好说明一下。第一种建树方法是这样的：

• 将所有关键点按 DFN 排序。
• 排序后相邻的关键点两两求出 LCA，将 LCA 和关键点放入数组 \(A\) 并去重。
• 将数组 \(A\) 的点按 DFN 排序。
• 对于所有 \(i>1\)，在虚树上将 \(A_i\) 连向 \(LCA(A_{i-1},A_i)\)。

第二种建树方法的本质是用单调栈维护一条右链，和笛卡尔树的 \(O(n)\) 建法有些相似，具体如下：

• 将所有关键点按 DFN 排序，在单调栈中加入点 \(1\)（为了方便）。
• 设当前想要加入关键点 \(a_i\)，首先获取它与栈顶的 \(LCA\)。
• 若 \(LCA\) 就为 \(a_{i-1}\)，直接加入 \(a_i\)。（它们在一条链上。）
• 否则，弹栈直到栈顶的 \(dep\) 小于等于 \(dep_{LCA}\)，此时不属于新右链的部分被弹完。若栈顶不为 \(LCA\)，加入 \(LCA\)。然后加入点 \(a_i\)。

题目

树

致没能场切的不难 T2。这个题显然就属于刚刚所说的第一类模型：它的树有无穷多个点与特殊形态，有 \(n\) 个编号为连续阶乘的关键点，并且发现，这个问题放在普通的树上是一个简单的换根 DP。因此可以考虑建虚树。能发现，求相邻的阶乘编号点的 LCA 的深度是相对简单的（这个场上推了出来），因此可以用第一种方法建虚树。然后换根 DP 就做完了。

SvT

题意：给定一个字符串，多次询问，每次询问给定若干后缀，求出这些后缀两两之间的 LCP 的和。

对原串建出后缀树，原问题就变成了：给定若干点，求出这些点两两之间的 LCA 的权值的和。显然可以建虚树求解，统计每个虚树上的点能作为多少询问点对的 LCA 即可。

5.Splay&LCT

概括

Splay 是一种平衡树，能处理很多线段树处理不了的东西，例如区间翻转，单点插入等等。它是一种二叉搜索树，并且它的复杂度基于势能分析，这就导致了它的代码看起来通常很暴力，但是只要加一个小小的 Splay 函数，它的复杂度就正确了。LCT 是一种动态树，它的实现基于 Splay，并且能处理比 Splay 更厉害的东西，而且在大多数情况下可以代替树剖。（理论复杂度甚至比树剖更优。）它在大部分情况下用来处理改变树形态的问题，总之很厉害就对了。

Splay 树基于 Splay 操作。Splay 操作基于 Rotate 操作。Rotate 操作基于左旋和右旋操作。这个东西不太好直接说明，可以放几张初学时乱画的图。

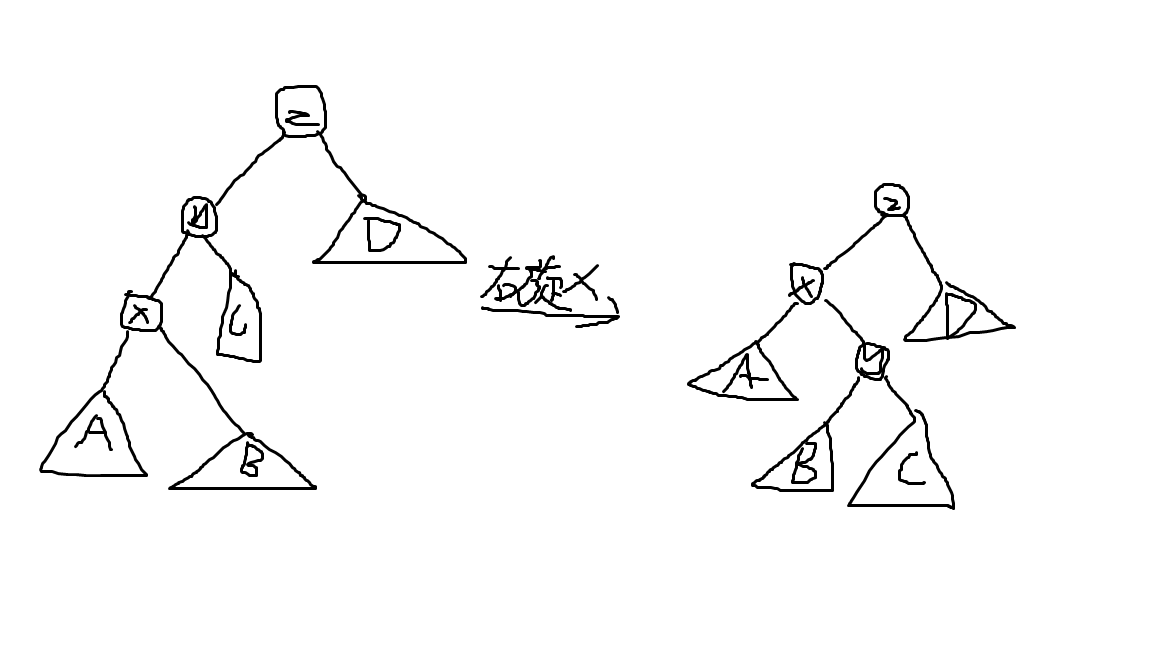
这张图说明了右旋操作。它将 \(x\) 右旋到 \(y\) 的上方，并改变了多对点的祖先后代关系。仔细分析归纳后可以写出各个点的变化（以右旋为例，左旋是对称的）：

• 首先明确，\(y=fa_x,z=fa_y,B=son_{x,1}\)。
• \(x\) 的变化：\(son_{x,1}=y,fa_x=z\)。
• \(y\) 的变化：\(son_{y,0}=B,fa_y=x\)。
• \(z\) 的变化：\(son_{z,0}=x\)。
• \(B\) 的变化：\(fa_B=y\)。

实现时，可以不将 \(B\) 单独存储，但这样就要注意赋值顺序。同时，不要修改 \(0\) 节点的信息，例如若 \(z=0\)，就不能修改 \(son_{z,0}\)。

多次 Rotate 组成了 Splay 操作。需要注意的是，只需要一次就能旋到指定点时，单旋一次即可。否则，需要区分同侧旋转和异侧旋转，它们操作的点是不同的。

然后是 LCT。LCT 的思想与树链剖分相似。它将树剖分成了一些链，只不过每一条链都用一棵 Splay 表示。Splay 与 Splay 之间用虚边连接。LCT 的核心操作是 Access 和 MakeRoot。Access 可以暴力地将当前点到根节点搓成一棵 Splay，MakeRoot 可以将当前点变成根。具体地，每棵 Splay 的根节点有一个虚父亲，它代表的是这棵 Splay 所对应的链里深度最小的那个点在原树上的父亲。根据这条虚边，就可以完成 Access 操作。而在 Access 的基础上，MakeRoot 操作显得更加简单了，只需要将当前点 Access 后，反转它所在的链就可以了。这个操作可以通过打 lazy 标记实现。

题目

一个动态树好题

LCT 维护基环树。具体 这篇文章 里有写。

6.SA&SAM

概括

SA，即后缀数组。SAM，即后缀自动机。两个都是非常重要的字符串算法。SA 主要用于处理后缀排序或者简单的后缀相关问题，而 SAM 主要侧重于将问题挂到 Parent 树上，树上问题的可操作性会比较强。SA 的小常 \(O(n\log n)\) 做法比较好理解，\(O(n)\) 做法我不会且实用性不强。SAM 的构造过程等需要一定研究才能理解，但是复杂度我不会证明。

SA

主要有三个有用的数组，\(sa\)，\(rk\) 和 \(ht\)。其中，\(sa_i\) 代表排名为 \(i\) 的是哪个后缀，\(ht_i\) 代表后缀 \(i\) 的排名。\(ht\) 后面再说。

存在 \(O(n\log n)\) 的倍增做法。

假设现在已经知道了所有 \([i,i+k-1]\) 子串的排名情况，考虑如何求 \([i,i+2k-1]\) 的排名情况。事实上，这可以看作一个简单的双关键字排序。把 \([i,i+k-1]\) 作为第一关键字，把 \([i+k,i+2k-1]\) 作为第二关键字。显然，做 \(O(\log n)\) 次排序后可以得到答案，如果每次排序都是 \(O(n\log n)\) 的，复杂度就是 \(O(n\log^2 n)\)。和二分+哈希不相上下。

但是可以发现，这种做法比二分+哈希有前途。具体来说，因为排名一定是 \(\leq n\) 的，所以可以做 \(O(n)\) 的基数排序。如果这样的话，复杂度就是 \(O(n\log n)\) 了，够用。需要注意的是，如果两个子串完全相同，为了后续排序，它们的 \(rk\) 也必须完全相同。

如果直接这样写常数还是比较大，所以有一些可以卡常的点：

• 不需要对两个关键字都做一遍排序，因为已经有一个关键字在前一轮排好了。
• 如果当前不同子串数量等于 \(n\)，直接退出。

求出来 \(sa\) 和 \(rk\) 后，就可以着手求 \(ht\) 数组了。'

\(ht_i\) 表示后缀 \(sa_i\) 和后缀 \(sa_{i-1}\) 的 LCP，特别地，\(ht_1=0\)。显然，有 \(O(n\log n)\) 的二分+哈希求法，但是这个问题也可以 \(O(n)\) 做。

有一个引理是这样的，\(ht_{rk_i} \geq ht_{rk_{i-1}} - 1\)。这是在阐述原串上相邻的两个后缀的 \(ht\) 关系，画图能够简单理解。所以可以从 \(1\) 到 \(n\) 枚举后缀，然后暴力 \(O(n)\) 计算。

SAM

SAM 有点像 SA 的加强版，但是实际上又不太像。SAM 最重要的结构是 Parent 树，树上每个节点都存着一个 \(\text{endpos}\) 等价类和长度 \(Len\)，代表以该等价类中每个点为结尾的长度相同的长度 \(\leq Len\) 的子串相同。而若一个等价类是另一个等价类的祖先，当且仅当祖先等价类包含子等价类。其实，Parent 树只是做题最重要的结构，SAM 本身最主要的结构是 Next DAG。这个 DAG 上的点是一个等价类，边就是在该等价类结尾处加上一个字符到达一个新等价类。

SAM 的构造方法是增量式构造。现在知道了前 \(i-1\) 个字符对应的 SAM，想要添加 \(s_i\)。首先建立一个新点 \(np\)，它是前缀 \(i\) 对应的等价类。然后找到前缀 \(i-1\) 对应的等价类，一旦这个等价类在 Next DAG 上没有权值为 \(s_i\) 的边，就添加一条，并把它连向 \(np\)。然后跳 Parent 树，直到跳到根或找到一个点有权值为 \(s_i\) 的边。此时需要将这个点指向的点 \(q\) 根据 \(Len\) 的关系分离出来。然后按照 \(\text{endpos}\) 等价类的定义改变 Next DAG 和 Parent 树就行了。

这里篇幅太短，说不清楚。复习可以看之前写的博客：SAM。

题目

品酒大会

简单题。首先对着原串的反串建出 SAM 和 Parent 树，容易发现对于任意一个节点，其 \(\text{endpos}\) 集合里的任意一对都是 \(Len\) 相似的。因此，统计个数只需要统计 Parent 树上每个节点的 \(\text{endpos}\) 集合大小再做后缀和。求美味度最大值也并不复杂，只需要统计子树内的最大值，次大值，最小值，次小值再分讨就行了。

[Ahoi2013]差异

普通的 SA 和笛卡尔树的合用。当然也可以单调栈做，但是笛卡尔树显然应用更广泛，有些题还需要启发式分治。这个题只有 LCP 那部分较难处理。求出 \(sa\)，\(rk\) 和 \(ht\)，把问题转到 \(ht\) 数组上。有一个显然的性质是，两个后缀的 LCP 就是它们在 \(sa\) 数组上 \(ht\) 的区间最小值。边界情况可能需要讨论。问题就变成了求出一个数列所有区间的最小值之和。建出 \(ht\) 数组的笛卡尔树，然后就可以做了。

奥利卡的诗

首先，推式子进行分析。发现要维护这样一个东西：每次往集合里加入一个字符串 \(S\)，定义一个字符串 \(A\) 的贡献为它在集合里每一个字符串中出现的次数之和的平方，求所有字符串的贡献之和。

看起来很不好做，但是可以放到先放到 Parent 树上。发现一个字符串子串出现的次数可以在其等价类那里统计，也就是说，一个等价类的贡献等于它的 \(v \times siz^2\)，其中 \(siz\) 是它所管辖的等价类的大小（即某个子串的出现次数），\(v\) 是 \(Len - Len_{Parent}\)，是个常量。每次修改操作就是对 \(siz\) 链加。那么再剖析一下就是两种操作。

• 修改操作：\(siz\) 链加。（点到根）
• 询问操作：询问树上所有点的权值和，其中单个点的权值为 \(v \times siz^2\)。

那么，直接树剖维护一次项、二次项等即可。

String

如果刚刚那个题是SAM+数据结构的基础题，那么这个题的技巧性要强得多。容易发现，对于 Parent 树上的一个节点，只有 \([l,r]\) 中最大和次大的 \(\text{endpos}\) 有效。那么可以把这个看成一个三元组 \((p,q,Len)\)，其中 \(Len\) 表示前缀 \(p\) 和前缀 \(q\) 的最长公共后缀。有了这些三元组过后，分讨发现询问可以主席树处理。但是，现在三元组个数不能保证，并且要求强制在线，也不能先处理出 Parent 树。

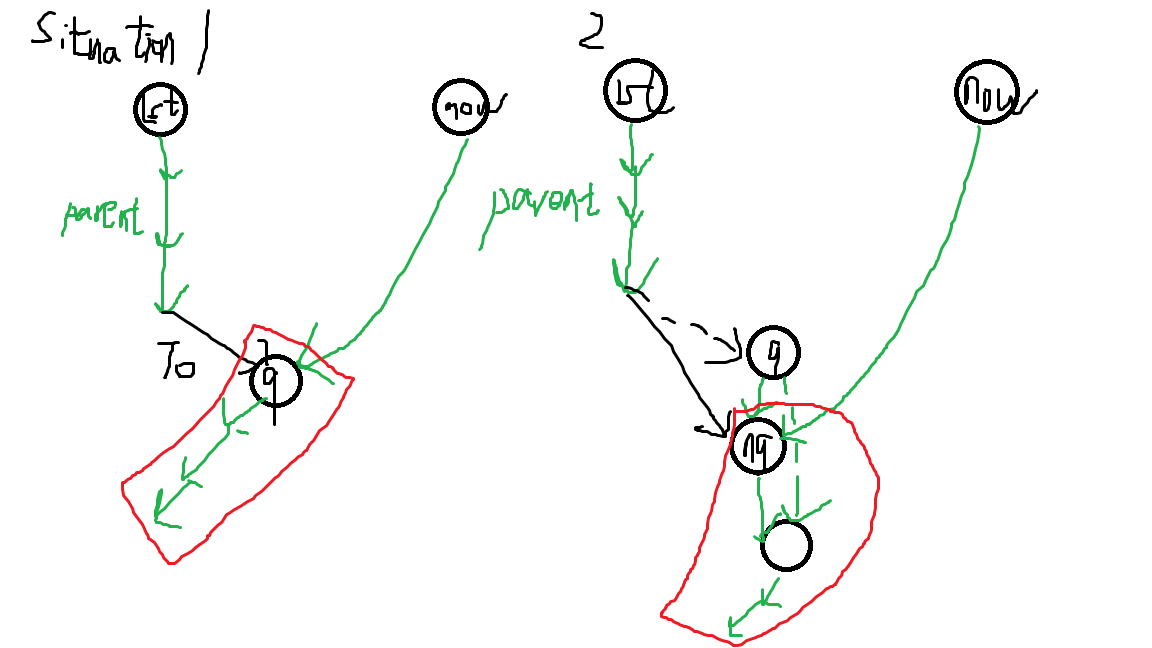
分讨画图后，发现 Parent 树的构造与变化过程是 LCT 好维护的。而且也不需要 MakeRoot 操作，Situation 2 可以看作在一棵 Splay 中进行了插入。这就有很多好的性质。首先，设每个点的颜色为它当前 \(\text{endpos}\) 集合的最大值。容易发现，当且仅当最大值被修改时才会产生一个新的三元组（只有此时最大值和次大值才可能变化）。再仔细分析可以知道，每一棵 Splay 的颜色是相同的。而每次产生新节点赋新值的操作其实是一个 Access 操作（从 \(np\) 开始），所以总三元组个数是 \(O(n\log n)\) 的（与 Access 操作总复杂度一样），套上主席树复杂度是 \(O(n \log^2 n)\) 的。

复习的时候可以看这个文章：谔谔。写得更详细。

总结

总而言之，SA 和 SAM 算是学过的可操作性比较强的字符串算法兼数据结构了。尤其是 SAM 非常有意义的特殊的 Parent 树结构，这就导致它能和很多东西套在一起。所以想要掌握它，必定也要熟练掌握一些数据结构技巧。LCT 和树剖是它的最佳搭档，LCT 用来在强制在线时维护 Parent 树，树剖来维护贡献（尤其是对给定串的所有前缀输出某个答案时）。能把它们掌握好其它的字符串算法也不用愁了。

7.SW

概括

一个用来求无向图全局最小割的算法。

算法流程：以某个权值函数为关键字向集合中不断加点，算答案，然后取出最后两个缩点，递归处理。

权值函数：\(w(u)=\sum\limits_{v\in S}w(u,v)\)。

我相信这个算法我是绝对不会忘的。

例题

无。

8.线性基

概括

这里写的是异或线性基。

给定一个数列 \(A\)，选一些数，求这些数的异或最大值。可以用异或线性基解决这个问题。\(A\) 能表示出来的数看似很多，实际上可以用一个长度为 \(O(\log V)\) 的数组 \(B\) 表示。即 \(A\) 能表示的数，\(B\) 也能表示，\(A\) 不能表示的数，\(B\) 也不能表示。这样的 \(B\) 怎么构造？

考虑现在插入一个数 \(A_i\)。从高位到低位依次遍历。设当前遍历到第 \(j\) 位，若 \(A_i\) 的第 \(j\) 位为 \(0\)，则跳过。否则若 \(B_j\) 为 \(0\)，将 \(B_j\) 赋值成 \(A_i\)，然后插入下一个数。否则将 \(A_i\) 赋值成 \(A_i\) \(\text{xor}\) \(B_j\)，然后遍历下一位。

当 \(A\) 中所有数都插入后，最后的 \(B\) 就是要求的异或线性基。可以发现，它是对的，并且它有若干性质，例如 \(B_j\) 如果不是 \(0\)，最高位就是第 \(j\) 位，\(B\) 中任意一个非空子集异或不为 \(0\) 等等。这能方便做很多事，例如刚刚的问题就可以从高位到低位直接贪心解决，只要看异或上 \(B_j\) 后答案是否变大就行了。

线性基套线段树分治的题不少，但是也有比较好用的时间戳线性基。

题目

[SCOI2016] 幸运数字

线性基合并是简单的，把一个线性基的每一个元素插入另一个就行了，但这样复杂度是 \(O(\log^2)\) 的，所以树剖过不去。考虑点分治，发现非常好做，每次维护重心到某个点的路径上的线性基就行了，单次查询也只需要合并两条单链的线性基，可以过。

但是有一种更加简单无脑的做法，就是树上倍增。处理出每个点到 \(2^k\) 级祖先的路径上的线性基，由于线性基是可合并信息，所以查询时合并的线性基个数是 \(O(1)\) 的，预处理的复杂度是 \(O(n\log n\log^2 V)\) 的，也可以过。

9.多项式

概括

虽然名义上叫做多项式，但是说成卷积貌似更好，总不能把 FWT 那一套也归成多项式乘法吧。FFT，NTT，FWT 均用来处理卷积问题。其中 FFT，NTT 用来处理形如 \(i+j=k\) 的卷积问题。FFT 的理论基于复数和单位根等等，实现也需要手写 double 的 complex 类，这就导致 FFT 常数较大且容易丢精。而 NTT 则完美地弥补了 FFT 的缺陷：它不需要 double 运算，它不需要手写 complex 类，它也不会丢精。但是取而代之的是新的缺陷：NTT 对模数的要求较为严格，且取模带来的常数也不容小觑。NTT 解决的是取模的卷积问题，需要的并不是单位根而是和单位根性质相似的原根。原根的存在性很严苛，并且因为想要构造出 \(N\) 次单位根 \(g^{\frac{φ(Mod)}{N}}\)，\(N\) 就必须是 \(φ(Mod)\) 的因数。

种种限制促使了 MTT 的诞生，即任意模数 NTT。它可以使用三模 NTT + CRT 合并答案实现，当然也可以用 FFT 拆系数实现。比较有意义且易懂的做法是 \(5\) 次 FFT，当然目前也有 \(4\) 次。它们各有优缺点吧。例如我认为 \(5\) 次 FFT 更好写。

FWT 可以通过一些巧妙的构造和与 FFT 相似的流程实现形如 \(i\) \(\text{and}\) \(j = k\)，\(i\) \(\text{or}\) \(j = k\)，\(i\) \(\text{xor}\) \(j=k\) 等等的卷积。也可以做子集反演。

真正的题目一般不是裸题。一般都是要自己找到卷积的形式再自己写出来。

题目

删点游戏：

经过一番推导后，发现要求各种长度的路径的出现次数。因为是路径相关问题，考虑点分治。发现这个东西点分治来做就相当于长度为 \(i\) 的单链加长度为 \(j\) 的单链可以合成长度为 \(i+j\) 的路径，权值为 \(cnt_i \times cnt_j\)，再减去算多的贡献。发现这个东西显然是一个卷积形式，可以卷积做。