谔谔

警告：本文中含有大量令人谔谔的不知所云的文字，请谨慎阅读。

警告：本文中含有大量令人谔谔的毫无艺术感的图片，请谨慎阅读。

警告：意识流。

警告：有（无）代码。

警告：柚子树是右子树的意思。

你已经被警告过了。

String

传送门

题目分析

还没有理解SAMLCTSplay的本质，所以做起来很困难。
容易发现的是，对于询问 \([l,r]\)，考虑 SAM 上的一个节点，只有在区间中的最大的和次大的 \(endpos\) 有效。那么就可以把这样的东西表示成一个三元组 \((p,q,Len)\)。\(p,q\) 为 \(endpos\)，\(Len\) 是前缀 \(p\) 和前缀 \(q\) 的最长公共后缀。添加时可能会让原来是最大和次大的不再是最大和次大的，但是这不会使答案错误。

先考虑有了三元组之后如何统计答案。

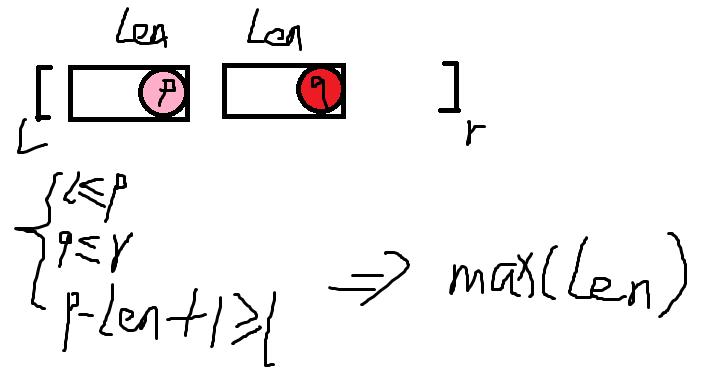
这种情况下，它们的 LCS(Suffix) 没有超出 \(l\)，答案即为 \(\max(len)\)。同时条件 \(3\) 是严格强于条件 \(1\) 的。那么，对于一个三元组，可以把它看做点 \((p-Len+1,q)\) 有 \(Len\) 的权值。但是直接这么看能发现这是一个动态二维偏序，不能 \(O(n\log n)\) 做。不过这样看有点傻，每次添加字符只会新增 \(q=r\) 的三元组。所以当维护 \(\leq r\) 的主席树时，主席树不会受到修改影响。具体地，每次新建一个字符，多开一棵主席树，复制前面一棵的节点，然后在上面加上 \(q=r\) 的三元组对应的下标与权值。每次查询就是查单棵主席树了。（我不太会数据结构，所以多写点。）

同理呢，情况 \(2\) 也只需要简单推导。

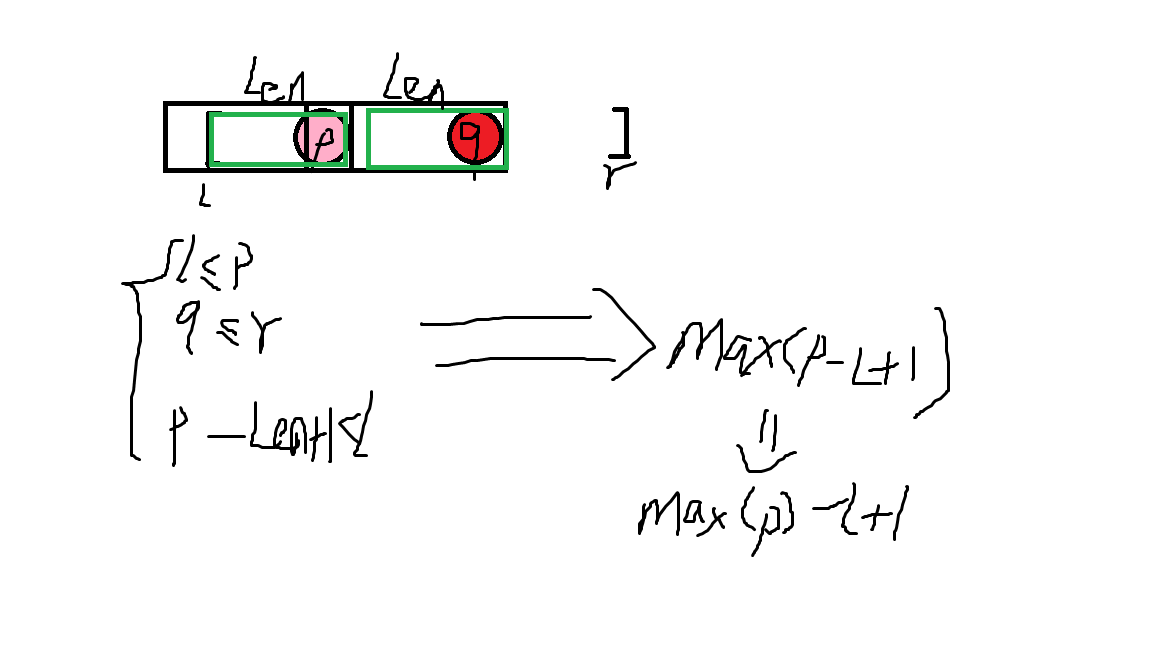
维护同上。

现在的问题就是怎么统计三元组。由于强制在线+插入字符，只能用 LCT 来维护 SAM（Parent树）。

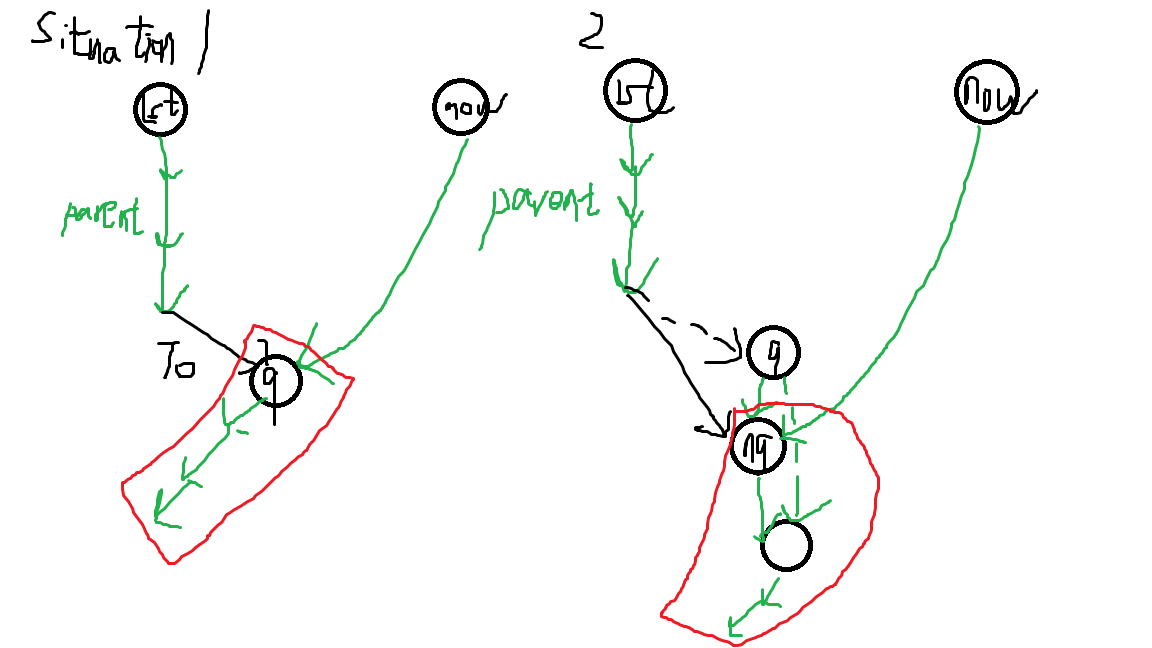
现在也有两个 SITUATION。红色部分就是 \(endpos\) 集合发生变化的节点。可以发现这就是一次 access 操作。还可以发现，只需要维护每个点最大的 \(endpos\) 就行了。这样加叶子的时候就相当于一次链覆盖（因为位置是递增的），而次大的就是原来的 \(endpos\)。因为是链覆盖，容易发现正常操作下每一个 Splay 都对应着同一个最大 \(endpos\)。

注意到这里说的是正常操作。SITUATION 2中的 cut 操作就属于不正常操作。因为它会 access，并且没有链覆盖，会打乱辅助树良好的结构。但是这里维护 SAM 的情况非常非常特殊，因为可以将有关 \(nq\) 的一系列的操作看做直接插入了一个新点。这样就可以直接在 Splay 上做了。

理解过后，具体的做法也出来了。插入点 \(nq\) 后，从新建点 \(np\) 也就是点 \(now\) 开始，进行 access(SPECIAL) 操作。找到一棵新的 Splay，将它的值覆盖成 \(np\) 前，先加入它与 \(np\) 的三元组。\(q\) 是它（辅助树上）在原树上最深的那个节点对应的前缀。这个简单分析可以得到，因为该辅助树上一定有 \(q\) 为前缀的对应节点。然后 \(Len\) 就是遇到的那个节点的 \(Len\)，因为它是和 \(q\) 的 \(LCA\)。

因为 access 总复杂度是 \(O(n\log n)\) 的，每次跳一棵 Splay 会加一个三元组，所以三元组个数是 \(O(n\log n)\) 的。主席树操作，总复杂度是 \(O(n \log^2 n)\) 的。

这个题真的很难。

注意事项

果然很多事情要上手写了才知道。

首先，因为 SAM 需要使用 Parent 树，所以必须把辅助树和原树分开存。并且只有在添加新边的时候才能更改辅助树。

然后，因为在一棵主席树上有多次修改，可以先将 Root[i-1] 复制到 Root[i] 上，然后传参时 &u 和 v 都传 Root[i]。感谢 geven 大神。

Counting Prefixes

传送门

老实说，这个题用 BEST 定理有些华而不实，但确实对理解 BEST 定理有很大帮助。

呵呵呵呵呵呵。待补。

一个动态树好题

传送门(Hydro的BZOJ)

题目分析

抽象 LCT。图论建模是容易的，每个方程从 \(i\) 连向 \(p_i\)，是个内向基环树森林。知道链头就可以唯一确定链尾。环上也可以直接解出来，但是如果无解或者有多解，那么这整棵基环树肯定都是无解或者有多解。

直接做就可以 \(O(nq)\) 了。当然，修改只有 \(20\%\)，也可以利用一下，但是应该是过不去的。

考虑正解。首先，LCT 怎么维护基环树森林？只要钦定环上的点为根，并且将其出边设为虚边就行了。这个一会分讨会说。修改就是 Link 操作和 Cut 操作，然后改点权。

然后考虑合并一下方程信息，比如说知道 \(x_2 \equiv k_1x_1+b_1\)，\(x_3 \equiv k_2x_2+b_2\)，直接代入，得到 \(x_3 \equiv k_1k_2x_1+k_2b_1+b_2\)。分析一下发现这个合并运算是满足结合律但是不满足交换律的，然后这个运算可以写成矩阵形式，这也说明了这一点。所以在 Splay 上合并就需要非常注意顺序，按深度从小到大。这直接导致了 MakeRoot 操作不能存在，这个稍微有点难搞。

先不考虑 MakeRoot 操作，考虑如何得到答案。

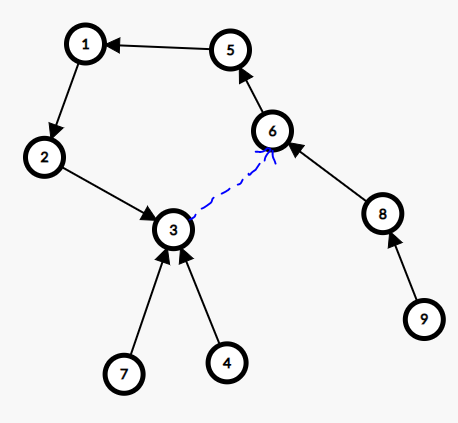
上图中，\(3\) 是根，\((3,6)\) 是虚边。现在，询问 \(9\)。如果方程 \(i\) 是 \(F_i\)，合并运算写成 \(\times\)，那么通过 \(F_2 \times F_1 \times F_5 \times F_6 \times F_8 \times F_9\)，可以得到 \(x_9\) 与 \(x_3\) 的方程关系。现在要求 \(x_3\)，通过 \(F_2 \times F_1 \times F_5 \times F_6\) 得到 \(x_6\) 与 \(x_3\) 的方程关系。然后又因为有 \(F_3\)，所以可以知道 \(x_3\) 与 \(x_3\) 的方程关系。解一下就出来了。

结合这个，可以发现一件事：不一定环上无解/有多解，最后就无解/有多解。求出来询问的数和根的方程关系中可能 \(k=0\)，也就是无关。这个时候询问的数就直接等于方程关系中的 \(b\)。（毕竟方程关系还是对的。）

事实上，这个过程中需要的信息只有某个节点到根的信息。（更具体地，根节点自身的信息要特殊考虑。）这说明，不需要 Split 操作。但是有 Link 和 Cut 操作。然后就有一个东西，是不需要 MakeRoot 的 Link 和 Cut 操作。这个怎么做？

void Cut(int x){
  Access(x);Splay(x);fa[S[x][0]]=0;S[x][0]=0;
}

void Link(int x,int y){
  Access(x);Splay(x);fa[x]=y;
}

这个东西是对的。先说 Cut 操作。先把 \(x\) Access 了。出现了一条实链，\(x\) 为其中深度最大的点。然后在辅助树中将它 Splay 到根。它的柚子树就空了，左子树是它到根的所有节点。然后把它和它的左子树断掉，Cut 结束。这里可能会有疑问，把 \(fa\) 设为 \(0\) 不会有问题吗？要是实链上方还有节点怎么办？这个实链是一直到根的，所以它上面一定没有节点了。

然后是 Link 操作。是类似的。唯一要注意的是，Access(x) 后，\(x\) 所在实链必定只有 \(x\) 一个点，直接将 \(fa_x\) 赋值成 \(y\) 是没有问题的。

最后是分讨和虚边维护问题。

只有两种情况：要么删的是虚边，要么不是。比较好做。

注意事项

其实情况不止两种，还是比较多。居然（几乎）一遍过，出乎意料。