SAM

前言：这只是一篇随笔，不保证啥啥啥的东西。

Next DAG：Next DAG，顾名思义，是一个搭个。对于弦乐器 \(S=\text{geven}\)，可以建造出这样的 Next DAG。

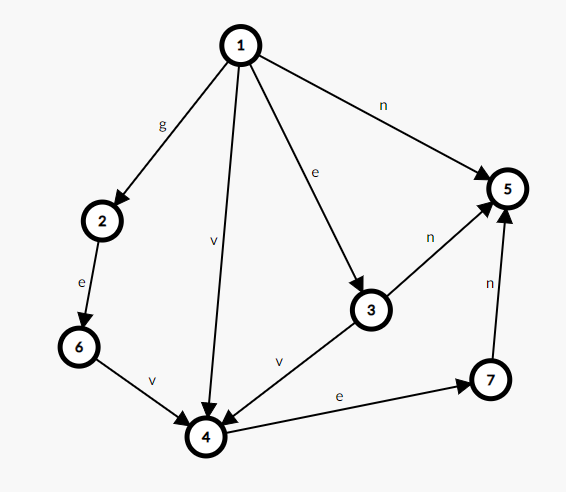
从 \(1\) 出发的一条路径可以构成一个原串的子串。把除 \(1\) 外每个点对应的路径写下来：
\(2:\{\text{g}\}\)。
\(3:\{\text{e}\}\)。
\(4:\{\text{gev,v,ev}\}\)。
\(5:\{\text{n,en,ven,even,geven}\}\)。
\(6:\{\text{ge}\}\)。
\(7:\{\text{eve,ve,geve}\}\)。
可以发现每个子串都唯一对应了一条路径，每条路径都唯一对应了一个子串。
且 \(S=\text{geven}\) 的终止态只有点 \(5\)。
Next DAG 的性质为：每个点对应的路径所对应的子串的 \(\text{endpos}\) 集合相同，即属于同一个 \(\text{endpos}\) 等价类。
容易证明，两个合法的 \(\text{endpos}\) 等价类要么是不交关系，要么是包含关系。
容易证明，一个 \(\text{endpos}\) 等价类里的一个结尾所对应的左端点必定是 \([x,y]\) 这样的一个区间，且所有 \(\text{endpos}\) 等价类对该结尾所有可能的左端点做了一个划分。
事实上，一个 \(\text{endpos}\) 等价类里所有的结尾都对应着相同的一些子串（呈后缀关系），由定义就可以证明，所以大多数情况只考虑一个结尾就行了。

这个图是会用到的，没错。

Parent 树/Fail 树：

因为 \(\text{endpos}\) 们的特殊的包含关系，它们一定形成一个树形结构。
具体来说，我们只需要把 A 连向 B，把 B 连向 C 就行了，B 一定是 A 的最小父集，C 一定是 B 的最小父集。设 \(len\) 为某个 \(\text{endpos}\) 等价类的最长子串长度，则这样连边 \(len\) 一定递减。
于是我们有了一棵 \(S=\text{geven}\) 的 Parent 树。

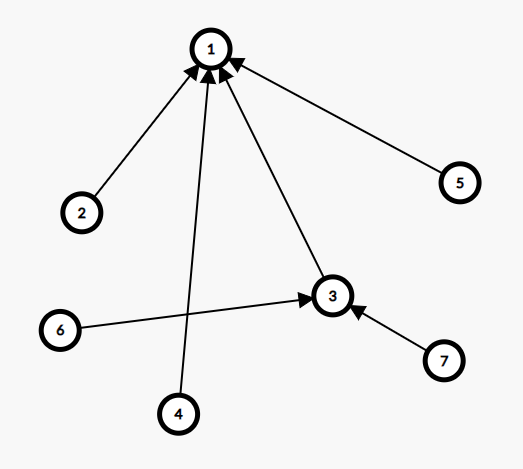
jr_zch 说，每个前缀都对应了 Parent 树上的一个叶子结点。

求法：
增量式构造。

当前加入了 \(S_i=c\)，上一个 \(i-1\) 对应的等价类为 \(lst\)。这个等价类一定是新出现的等价类，因为原来都没有 \(\text{endpos}\) 等价类含有 \(i-1\)。
于是，对于 \(i\)，也新建一个等价类，其对应的点为 \(np\)。这个等价类的代表字串是 \(S[1,i]\)，肯定只出现过一次，所以 \(\text{endpos}=\{i\}\)。所以 \(i-1\) 新建的那个 \(\text{endpos}=\{i-1\}\) 是肯定的。
\(len_{np}\) 更新为 \(len_{lst}+1\)，现在考虑求 \(Parent_{np}\)。从 \(lst\) 开始，一直往上跳 \(p\)。如果说不存在 \(nxt_{p,c}\)，就说明在等价类 \(p\) 中的任意一个子串后加一个 \(c\)，都在 \(S[1,i]\) 中只出现过一次，与 \(np\) 等价。
如果一直找不到一个不等价的 \(p\)，说明字符 \(c\) 第一次出现，\(Parent_{np}\) 当然可以直接赋值为 \(1\)，\(go_{1,c}=np\)。
否则就有点麻烦。假设这个不等价的就是 \(p\)，记录 \(q = go_{p,c}\)。

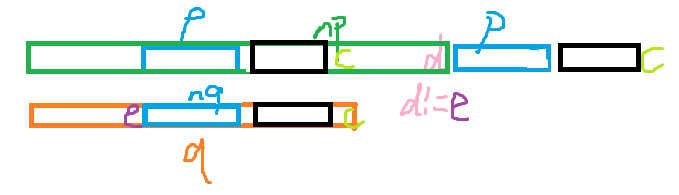
然后大概就是这么一个局势。\(len_q\) 不是所有后缀都是我们想要的。具体来说，若 \(len_q=len_p+1\)，则 q 的所有后缀都是合法的，可以直接替换掉 \(p\)，\(Parent_{np}\) 直接赋值成 \(q\)。这很好。

但是如果 \(len_q>len_p+1\)，我们想要的只有 \(q\) 中蓝色黑色与 \(c\) 的那一部分。只有那一部分的后缀 \(\text{endpos}\) 才会 insert 一个 \(i\)。所以 \(q\) 中不同后缀的 \(\text{endpos}\) 变得不同了，我们必须将其分裂成两个等价类，设右边蓝色黑色与 \(c\) 的为 \(nq\)，而 \(q\) 现在只能指左边橙色的，那么 \(Parent_q\) 和 \(Parent_{np}\) 都应该赋值成 \(nq\)。现在，\(p\) 及它到根链上所有的点如果原来 \(go_{c}\) 是 \(q\)，那么现在只能指到 \(nq\)，然后就做完了。