「算法笔记」线性基
修改于 2023 年不知道哪个月。
2020 年写的(已折叠)
一、定义
线性基是向量空间的一组基,通常可以解决有关异或的一些题目。
通俗一点的讲法就是由一个集合构造出来的另一个集合,它的性质如下:
-
线性基的元素能 相互异或 得到原集合的元素的 所有 相互异或得到的值,并且线性基是满足该性质的 最小的 集合。
-
线性基没有异或和为 \(0\) 的子集。
-
线性基中每个元素的异或方案唯一,即线性基中不同的异或组合异或出的数都是不同的。
-
线性基中每个元素的二进制最高位互不相同。
每个序列都拥有至少一个线性基。线性基中的第 \(i\) 个数在二进制下最高位 \(1\) 的位置为 \(i\)。
二、线性基的操作
1. 插入与判断
具体来说,就是向一个集合中插入一个元素,同时维护这个集合的线性基。
令插入的数为 \(x\)。将 \(x\) 转为二进制。
设 \(x\) 在二进制下的最高位 \(1\) 的位置为 \(i\)。
-
若线性基中的第 \(i\) 个数不存在,则直接令线性基的第 \(i\) 个数为 \(x\)。结束。
-
否则,若线性基中的第 \(i\) 个数已经有值 \(a_i\),则令 \(x=x\text{ xor }a_i\)。并重复上述操作直到 \(x=0\)(即将异或后得到的 \(x\) 重新插入线性基)。
若结束时 \(x=0\),则原来的线性基中已经可以表示出原先的 \(x\) 了;反之,则说明此时往线性基中加入了一个新元素,此时也能表示 \(x\) 了。
void insert(int x){ for(int i=N-1;i>=0;i--){ //从高位向低位扫 if(((x>>i)&1)==0) continue; if(!a[i]){a[i]=x;break;} //线性基的第 i 个数不存在 else x^=a[i]; } }
判断一个数是否可以被线性基中的数异或得到:用上面插入的方法判断,若结束时 \(x=0\),则能表示;反之,不能表示。
2. 合并
两个线性基是可以暴力合并的。
对于集合 \(A,B\),把 \(B\) 线性基中的元素依次插入到 \(A\) 的线性基中即可得到 \(A\cup B\) 的线性基。
三、线性基的应用
1. 查询异或最小值
注意这里的最小值,指的是线性基中取若干个数异或可以得到的数的最小值。
线性基中的元素最高位 \(1\) 的位置都不同。考虑线性基中最小的数,它异或上其他数显然会变大。所以答案就是线性基中所有元素中最小的那个。
而若是查询一个集合中取若干个数(而不是这个集合的线性基),使得它们的异或和最小,就要再看看最小值是否有可能为 \(0\),即判断在插入集合元素的过程中,是否存在结束时 \(x=0\) 的情况(说明原来的线性基中已经可以表示出原先的 \(x\) 了)。
2. 查询异或最大值
具体来说,就是查询一个集合中取若干个数,使得它们的异或和最大。
先构造出这个集合的线性基。
考虑贪心,从高到低位扫,由于若当前扫到第 \(i\) 个数,意味着可以保证答案的第 \(i\) 位为 \(1\),且后面没有机会改变第 \(i\) 位,所以若异或上当前扫到的 \(a_i\) 会使答案变大,就把答案异或上 \(a_i\)。其中 \(a_i\) 为线性基中的第 \(i\) 个数。
具体地,若此时的答案异或上 \(a_i\) 能使答案变大(其实就是在二进制下 \(a_i\) 的第 \(i\) 位为 \(1\) 且答案的第 \(i\) 位为 \(0\) 时),则将答案异或上 \(a_i\)。扫完线性基之后得到的答案一定就是集合中的数可以通过异或表示出来的最大值。
int query(){ //查询异或最大值 int ans=0; for(int i=N-1;i>=0;i--) ans=max(ans,ans^a[i]); return ans; }
3. 查询异或第 k 小
参考 Menci 的博客 qwq。
给出一个集合,求其第 \(k\) 小的子集异或和。
Part 1. 首先,求出这个集合的线性基 \(a\),选择线性基的一个 非空子集 共有 \(2^{|a|}-1\) 种方案(能通过异或表示出 \(2^{|a|}-1\) 个数)。如果 \(|a|<n\),则说明至少有一个没有被插入到线性基中的数可以被线性基中的数表示出来,选择线性基中的一些数与这个数,可以得到其异或和为 \(0\),这样有 \(2^{|a|}\) 种方案。
然后,考虑给出线性基,求选择若干数可以组成的第 \(k\) 小的数(由于线性基没有异或和为 \(0\) 的子集,所以要特殊考虑 \(0\),若能异或表示出 \(0\),那么 \(0\) 肯定是最小值,则要把查询的 \(k\) 减 \(1\))。
Part 2. 将 \(k\) 表示为一个长度为 \(|a|\) 的二进制数(若不足,可在高位补 \(0\))。\(k\) 的二进制排列符合以下性质:
- 1. 选择「较高位上的 \(1\)」比「较低位上的 \(1\)」更能使 \(k\) 更大。
- 2. 选择「较高位上的 \(1\)」后,再选择「更低位上的 \(1\)」一定会使 \(k\) 更大。
线性基的 \(|a|\) 个元素控制了异或后结果的 \(|a|\) 个二进制位,而二进制数的规律恰好与从线性基中选数的两条规律 相对应:
- 1. 选择「控制较高位上的 \(1\) 的元素」比「控制较低位上的 \(1\) 的元素」更能使异或和更大。
- 2. 选择「控制较高位上的 \(1\) 的元素」后,再选择「控制更低位上 \(1\) 的元素」一定会使异或和更大。
于是就可以:枚举 \(k\) 所有为 \(1\) 的二进制位,如果第 \(i\) 位为 \(1\),则将线性基中控制的第 \(i\) 小的二进制位的元素异或到答案中。
//HDU 3949 #include<bits/stdc++.h> #define int long long using namespace std; const int N=60; int t,n,q,x,k,a[N],b[N],cnt,tot; bool flag; void insert(int x){ for(int i=N-1;i>=0;i--){ if(((x>>i)&1)==0) continue; if(!a[i]){a[i]=x;break;} else x^=a[i]; } if(!x) flag=1; //flag: 标记是否存在异或和为 0 的情况 } int query(int k){ if(k>(1ll<<cnt)-1) return -1; int ans=0; for(int i=0;i<cnt;i++) if((k>>i)&1) ans^=b[i]; return ans; } signed main(){ scanf("%lld",&t); while(t--){ scanf("%lld",&n),flag=0,cnt=0,fill(a,a+N,0); for(int i=1;i<=n;i++) scanf("%lld",&x),insert(x); for(int i=N-1;i>=0;i--) for(int j=i-1;j>=0;j--) if((a[i]>>j)&1) a[i]^=a[j]; //重构线性基,将每一位都独立,使每一位的选择都不会影响下一位。相当于线性基中的元素与其它元素异或,得到的仍满足线性基的性质。此时线性基中任一元素都要满足:最高位的 1 在线性基中只出现一次。 for(int i=0;i<N;i++) if(a[i]) b[cnt++]=a[i]; //b[i] 表示线性基中控制第 i 小的二进制位的元素 scanf("%lld",&q),printf("Case #%lld:\n",++tot); while(q--){ scanf("%lld",&k),k-=flag; printf("%lld\n",query(k)); } } return 0; }
4. 求子集异或值排名
给出一个集合,以及一个数 \(x\)。这个集合的所有子集(可以为空)的异或值从小到大排序得到序列 \(\{b_i\}\),求 \(x\) 在 \(\{b_i\}\) 中第一次出现的下标。
首先,求出这个集合的线性基 \(a\)。
考虑线性基所控制的某个二进制位,如果 \(x\) 的这一位为 \(1\),那么线性基中控制这一位的元素一定被选择,这样可以求出 \(x\) 在去重后的 \(\{b_i\}\) 中第一次出现的下标。
之后,计算每个重复的数字出现了多少次。设给定集合中不在线性基中的数的集合为 \(S\),显然 \(|S|=n-|a|\)。考虑它的一个子集 \(S'\)(可以为空),\(S'\) 的异或和一定可以 唯一表示 为 \(a\) 中若干个数的异或和,将它们都异或起来,就可以得到 \(0\)。那么就有 \(2^{n-|a|}\) 中方案得到 \(0\)。所以,对于每一个 \(b_i\),它的出现次数至少为 \(2^{n-|a|}\)。接着证明它的上界,假设在 \(S\) 中任意选,最终都可以凑出这个数,而选择 \(a\) 中的数的方案一定是唯一的,即上界也为 \(2^{n-|a|}\)。
求出线性基中子集异或和小于 \(x\) 的子集个数 \(cnt\),答案为 \(cnt \times 2^{n-|a|}+1\)。
//BZOJ 2844 #include<bits/stdc++.h> #define int long long using namespace std; const int N=60,mod=10086; int n,x,k,a[N],b[N],cnt,ans; int mul(int x,int n,int mod){ int ans=mod!=1; for(x%=mod;n;n>>=1,x=x*x%mod) if(n&1) ans=ans*x%mod; return ans; } void insert(int x){ for(int i=N-1;i>=0;i--){ if(((x>>i)&1)==0) continue; if(!a[i]){a[i]=x;break;} else x^=a[i]; } } signed main(){ scanf("%lld",&n); for(int i=1;i<=n;i++) scanf("%lld",&x),insert(x); scanf("%lld",&k); for(int i=0;i<N;i++) if(a[i]) b[cnt++]=i; //转化后显然对最高位的 1 不影响,实现时可以不写“查询异或第 k 小”中「重构线性基使最高位的 1 在线性基中只出现一次」的部分。 for(int i=0;i<cnt;i++) if((k>>b[i])&1) ans+=(1ll<<i),ans%=mod; //ans: k 在去重后的「所有子集(可以为空)的异或值从小到大排序得到序列」中的排名 printf("%lld\n",(ans%mod*mul(2,n-cnt,mod)%mod+1)%mod); return 0; }
四、例题
1. Luogu P3857 彩灯
题目大意:有 \(n\) 个彩灯,并且有 \(m\) 个开关控制它们。当一个开关被按下的时候,它会把所有它控制的彩灯改变状态(即亮变成不亮,不亮变成亮)。给定每个开关所控制彩灯的范围,求这些彩灯的样式的方案数。答案对 \(2008\) 取模。
(初始时所有彩灯都是不亮的状态。两种样式不同当且仅当有至少一个彩灯的状态不同。)
Solution:
考虑把开关的控制转化为将所有彩灯的状态异或上一个数 \(x\)。根据异或的性质,该转化成立。
构造出 \(x\) 的集合的线性基,求出线性基中元素的数量 \(k\)。
由于线性基中的每个元素都有选与不选两种情况,并且线性基中不同的异或组合异或出的数都是不同的(线性基的性质),所以答案就是 \(2^k\)。
#include<bits/stdc++.h> #define int long long using namespace std; const int N=60; int n,m,x,a[N]; char s[N]; void insert(int x){ for(int i=N-1;i>=0;i--){ if(((x>>i)&1)==0) continue; if(!a[i]){a[i]=x;break;} else x^=a[i]; } } int query(){ //求出线性基中元素的数量 int cnt=0; for(int i=N-1;i>=0;i--) if(a[i]) cnt++; return cnt; } signed main(){ scanf("%lld%lld",&n,&m); for(int i=1;i<=m;i++){ scanf("%s",s+1),x=0; for(int j=1;j<=n;j++) if(s[j]=='O') x|=(1ll<<(j-1)); insert(x); } printf("%lld\n",(1ll<<query())%2008); return 0; }
2. Luogu P4151 最大 XOR 和路径
题目大意:给一个 \(n\) 个点 \(m\) 条边的无向有权图,可能有重边或自环,保证图连通。求从 \(1\to n\) 的路径的最大异或和。
路径可以重复经过某些点或边,当一条边在路径中出现了多次时,其权值在计算异或和时也要被计算相应多的次数。
\(n\leq 5\times 10^4,m\leq 10^5,d_i\leq 10^{18}\),其中 \(d_i\) 为边权。
Solution:
先考虑不经过环的情况(即链的情况),找到一条路径。
考虑增广。如图,从某一点开始,经过一个环,再原路返回(这个图有点抽象……粉色的是同一条路径)。

往返的路径两次异或后对答案的贡献为 \(0\),所以只需考虑环的异或和。增广的路径就是环上的路径。
由于保证图为连通图,所以每个环都能走到。
把所有环的异或和丢进线性基,选一条链作为初值,求异或和最大值。
那么如何选择作为初值的链?假设 \(1\to n\) 的路径有 \(a\) 和 \(b\) 两条,并且我们选择了 \(a\) 作为初值。若 \(b\) 更优,由于 \(a\) 和 \(b\) 共同组成一个环,且所有环的价值都已经丢进了线性基,而 \(a\) 的异或和异或上 \(a\) 和 \(b\) 共同组成的环的异或和,就能得到 \(b\) 的异或和。求最大值时一定会发现异或上这个环的异或和会使答案更优,从而得到 \(b\) 的异或和。
\(1\to n\) 的路径一定会两两组成若干个环,无论选择哪条链作为初值,最终都可以得到答案。
#include<bits/stdc++.h> #define int long long using namespace std; const int N=1e5+5,M=61; int n,m,x,y,z,cnt,hd[N],to[N<<1],nxt[N<<1],val[N<<1],a[M],d[N]; bool vis[N]; void add(int x,int y,int z){ to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt,val[cnt]=z; } void insert(int x){ for(int i=M-1;i>=0;i--){ if(((x>>i)&1)==0) continue; if(!a[i]){a[i]=x;break;} else x^=a[i]; } } int query(int x){ int ans=x; for(int i=M-1;i>=0;i--) ans=max(ans,ans^a[i]); return ans; } void dfs(int x){ vis[x]=1; for(int i=hd[x];i;i=nxt[i]){ int y=to[i],z=val[i]; if(!vis[y]) d[y]=d[x]^z,dfs(y); else insert(d[x]^d[y]^z); //将环的异或和丢进线性基 } } signed main(){ scanf("%lld%lld",&n,&m); for(int i=1;i<=m;i++){ scanf("%lld%lld%lld",&x,&y,&z); add(x,y,z),add(y,x,z); } dfs(1),printf("%lld\n",query(d[n])); return 0; }
3. Luogu P4301 新 Nim 游戏
题目大意:传统 \(\text{Nim}\) 游戏:现在有 \(n\) 堆石子,第 \(i\) 堆有 \(a_i\) 个。两人轮流操作,每人每次可以从任选一堆中取走任意多个石子,但是不能不取。取走最后一个石子的人获胜(即无法再取的人就输了)。
新 \(\text{Nim}\) 游戏:第一轮,先手和后手可以取走若干个整堆的石子,可以一堆都不拿,但不能全部取走。接下来为传统 \(\text{Nim}\) 游戏。
问先手第一轮拿的石子数目的最小值。若不能保证取胜,输出 \(-1\)。
\(1\leq n\leq 100,1\leq a_i\leq 10^9\)。
Solution:
传统 \(\text{Nim}\) 游戏先手必胜,当且仅当 \(a_1\oplus a_2\oplus \cdots \oplus a_n\neq 0\)。
所以,若先手取完石子后,后手无论怎么取,都不能使剩余石子堆的异或和为 \(0\)(异或和为 \(0\) 意味着后手必胜),则先手必胜。
那么,在新 \(\text{Nim}\) 游戏中先手必胜,当且仅当先手取完石子后不存在剩余石子堆集中的子集,使得它的异或和为 \(0\)。
考虑线性基。在插入线性基时,若结束时 \(x=0\),意味着原来的线性基中已经可以通过异或表示出原先的 \(x\) 了,那么 \(x\) 与线性基中表示 \(x\) 的数异或起来就是 \(0\)。为了使后手无法使石子堆的异或和为 \(0\),先手就要把 \(x\) 取走。
于是问题转化为如何使第一轮拿的石子数目最小。
贪心:从大到小,能取则取(即结束时 \(x=0\) 时就取,否则插入线性基)。
#include<bits/stdc++.h> #define int long long using namespace std; const int N=110,M=60; int n,p[N],a[M],ans; bool solve(int x){ for(int i=M-1;i>=0;i--){ if(((x>>i)&1)==0) continue; if(!a[i]){a[i]=x;break;} else x^=a[i]; } return x==0; } signed main(){ scanf("%lld",&n); for(int i=1;i<=n;i++) scanf("%lld",&p[i]); sort(p+1,p+1+n,greater<int>()); for(int i=1;i<=n;i++) if(solve(p[i])) ans+=p[i]; printf("%lld\n",ans); return 0; }
4. Luogu P3292 幸运数字
题目大意:给定一棵 \(n\) 个节点的树。求点 \(x\) 到 \(y\) 的简单路径上,任意选择若干个点的点权异或和的最大值。
\(n\leq 2\times 10^4,q\leq 2\times 10^5,w\leq 2^{60}\),其中 \(w\) 为点权。
Solution:
设点权的最大值为 \(w\)。
两个线性基是可以暴力合并的。对于集合 \(A,B\),把 \(B\) 线性基中的元素依次插入到 \(A\) 的线性基中即可得到 \(A\cup B\) 的线性基。定义 \(\text{merge}\) 运算合并两个线性基。显然 \(\text{merge}\) 运算的复杂度是 \(\mathcal{O(\log^2 w)}\) 的。
考虑树上倍增。设 \(f_{i,j}\) 表示节点 \(i\) 向上跳 \(2^j\) 步所到达的节点编号,\(g_{i,j}\) 表示节点 \(i\) 向上跳 \(2^j\) 步所经过结点(不包括节点 \(i\))的点权组成的线性基。则有:\(f_{i,j}=f_{f_{i,j-1\ \ }\ ,j-1},g_{i,j}=g_{i,j-1}\text{ merge }g_{f_{i,j-1\ \ }\ ,j-1}\)。
可以通过 DFS 预处理出 \(f\) 与 \(g\)。
对于每一组询问 \((x,y)\),令 \(t=\text{lca}(x,y)\)。我们把 \((x,y)\) 的路径拆成 \((x,t)\) 和 \((y,t)\) 两条路径,分别 RMQ。具体地,以 \((x,t)\) 为例,令 \(k=\log_{2}({dep}_x-{dep}_t+1)\),令 \(\text{jump}(x,k)\) 为 \(x\) 向上跳 \(k\) 步所到达的节点标号,把 \(g_{x,k}\) 和 \(g_{\text{jump}(x,{dep}_x-{dep}_t+1-2^k),k}\) 合并,求出合并得到的线性基的最大异或和即可。
#include<bits/stdc++.h> #define int long long using namespace std; const int N=2e4+5,M=60; int n,q,a[N],x,y,cnt,hd[N],to[N<<1],nxt[N<<1],f[N][25],dep[N],t,k; struct node{ int a[M]; void insert(int x){ for(int i=M-1;i>=0;i--){ if(((x>>i)&1)==0) continue; if(!a[i]){a[i]=x;break;} else x^=a[i]; } } int query(){ //求最大异或和 int ans=0; for(int i=M-1;i>=0;i--) ans=max(ans,ans^a[i]); return ans; } }g[N][25],ans; node operator + (node x,node y){ //合并 x 和 y node res=x; for(int i=0;i<M;i++) if(y.a[i]) res.insert(y.a[i]); return res; } void add(int x,int y){ to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt; } void dfs(int x,int fa){ dep[x]=dep[fa]+1,g[x][0].insert(a[x]); for(int i=0;i<=19;i++) f[x][i+1]=f[f[x][i]][i],g[x][i+1]=g[x][i]+g[f[x][i]][i]; for(int i=hd[x];i;i=nxt[i]){ int y=to[i]; if(y==fa) continue; f[y][0]=x,dfs(y,x); } } int LCA(int x,int y){ //LCA if(dep[x]<dep[y]) swap(x,y); for(int i=20;i>=0;i--){ if(dep[f[x][i]]>=dep[y]) x=f[x][i]; if(x==y) return x; } for(int i=20;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i]; return f[x][0]; } int get(int x,int k){ //求 x 向上跳 k 步所到达的节点标号 for(int i=20;i>=0;i--) if((k>>i)&1) x=f[x][i]; return x; } signed main(){ scanf("%lld%lld",&n,&q); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); for(int i=1;i<n;i++){ scanf("%lld%lld",&x,&y); add(x,y),add(y,x); } dfs(1,0); //预处理出 f 和 g while(q--){ scanf("%lld%lld",&x,&y),t=LCA(x,y); k=log(dep[x]-dep[t]+1)/log(2),ans=g[x][k]; if(dep[x]-dep[t]+1!=(1<<k)) ans=ans+g[get(x,dep[x]-dep[t]+1-(1<<k))][k]; k=log(dep[y]-dep[t]+1)/log(2),ans=ans+g[y][k]; if(dep[y]-dep[t]+1!=(1<<k)) ans=ans+g[get(y,dep[y]-dep[t]+1-(1<<k))][k]; printf("%lld\n",ans.query()); } return 0; }
5. BZOJ 3569 DZY Loves Chinese II
题目大意:给定一张 \(n\) 个点 \(m\) 条边的无向连通图,多次询问,每次询问删掉 \(k\) 条边后图是否连通。询问相互独立,强制在线,\(k\) 条边的编号需异或之前询问答案为连通的数量。
\(n\leq 10^5,m\leq 5\times 10^5,q\leq 5\times 10^4,1\leq k\leq 15\),保证没有重边和自环。
Solution:
考虑把无向连通图拆成一棵树和一些边。
对于每条非树边,我们随机一个权值给它。对于树边,它的权值就是所有覆盖它的非树边的权值的异或和。
那么删掉 \(k\) 条边后图不连通,当且仅当这 \(k\) 条边中存在一个子集的权值异或和为 \(0\),即把一条树边以及覆盖它的非树边都删去了。
线性基维护即可。
#include<bits/stdc++.h> #define int long long using namespace std; const int N=1e5+5,M=5e5+5,K=60; int n,m,q,x,y,cnt,hd[N],to[M<<1],nxt[M<<1],id[M<<1],a[K],k,w[M<<1],d[N],ans; bool vis[N],flag; void add(int x,int y,int z){ to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt,id[cnt]=z; } void dfs(int x,int fa){ vis[x]=1; for(int i=hd[x];i;i=nxt[i]){ int y=to[i],z=id[i]; if(y==fa) continue; if(vis[y]){ if(!w[z]) w[z]=rand()+1,d[x]^=w[z],d[y]^=w[z]; //对于非树边,随机一个权值 } else dfs(y,x),w[z]=d[y],d[x]^=d[y]; //树边的权值 } } bool solve(int x){ for(int i=K-1;i>=0;i--){ if(((x>>i)&1)==0) continue; if(!a[i]){a[i]=x;break;} else x^=a[i]; } return x==0; } signed main(){ scanf("%lld%lld",&n,&m); for(int i=1;i<=m;i++){ scanf("%lld%lld",&x,&y); add(x,y,i),add(y,x,i); } dfs(1,0),scanf("%lld",&q); while(q--){ scanf("%lld",&k),flag=1,fill(a,a+K,0); for(int i=1;i<=k;i++){ scanf("%lld",&x); if(solve(w[x^ans])) flag=0; //存在异或和为 0 的情况 } puts(flag?"Connected":"Disconnected"),ans+=flag; } return 0; }
2022 年写的(已折叠)
一、前置知识
-
线性相关:对于向量 \(a_1,a_2,\cdots,a_n\),如果存在一组 \(k\)(\(k_i\) 不全为 \(0\))使得 \(k_1a_1+k_2a_2+\cdots+k_na_n=0\),则称它们是线性相关的,否则是线性无关的。
比如 \(a_1=(1,0),a_2=(2,0)\),\(2a_1+(-1)a_2=0\),所以是线性相关的。
-
线性组合 & 张成空间:对于向量 \(a_1,a_2,\cdots,a_n\),\(k_1a_1+k_2a_2+\cdots+k_na_n=x\),则称 \(x\) 为 \(a_i\) 的线性组合。所有这样的 \(x\) 组成的集合称为 \(a_i\) 的张成空间,记作 \(\text{span}(a)\)。
-
基:对于向量集合 \(a,b\),\(b\) 是 \(a\) 的一组基当且仅当 \(\text{span}(b)=a\) 且 \(b\) 线性无关。
比如三维空间,\((1,0,0),(0,1,0),(0,0,1)\) 能表示出所有 \((x,y,z)\),这就是一组基。同理,\(n\) 维空间基的大小为 \(n\)。
-
\(a\) 的任何真子集都不是 \(\text{span}(a)\) 的基。
由 \(a\) 线性无关,去掉任意一个向量,其余的都无法将其拼出来,显然也无法张成原来的 \(\text{span}(a)\)。
-
\(\text{span}(a)\) 中所有的向量,被 \(a\) 中向量表示出来的方案唯一。
若有两种不同的方案,相减之后则可得出 \(a\) 线性有关,矛盾。
-
若向量集合 \(c\) 线性有关,存在 \(a\subsetneq c\) 使得 \(\text{span}(a)=\text{span}(c)\)。
因为 \(c\) 线性有关,可以用剩下的向量来表示丢掉的那个向量。
-
二、线性基
1. 定义
解决和异或有关的一类问题。把每个数看作每一维为 \(0/1\) 的向量(二进制),而异或是 \(\bmod 2\) 意义下的向量加法,故转化为线性代数问题。
具体地,定义整数序列 \(a\) 的张成空间 \(\text{span}(a)\) 为,它们对应向量集在 \(\bmod 2\) 意义下的张成空间。其实际意义为 \(a\) 所有子集的异或和组成的集合。那么 线性基 就是 \(\text{span}(a)\) 的一组基。
显然,一个序列的线性基并不唯一,假设 \(b\) 为 \(a\) 的一组线性基,那么任意选择 \(i,j\) 并令 \(b_i\gets b_i\oplus b_j\),得到的 \(b\) 仍为 \(a\) 的线性基。
2. 求法
考虑动态维护 \(a\) 的线性基 \(b\),对于每一个 \(a_i\),查看其是否能被 \(b\) 中的数表示出来,如果不能,将其加入 \(b\);否则,加入 \(a_i\) 后 \(b\) 就不是线性无关的了,不符合线性基的定义。但不管是哪一种,\(a_i\) 都能被表示出来了。
怎么检验 \(a_i\) 是否能被 \(b\) 表示?高斯消元,考虑 \(a_i\) 的最高位 \(x\),如果 \(b\) 中存在某个向量 \(v\) 满足 \(v\) 的最高位也是 \(x\),就用 \(v\) 去消 \(a_i\)(\(a_i\gets a_i\oplus v\)),如果最后 \(a_i=0\) 则能被表示,否则不能。
实现时,并不需要写 \(|b|^3\) 的高斯消元。设 \(v_i\) 表示最高位的 \(1\) 为第 \(i\) 位的向量,加入 \(x\) 时,就从高到低枚举第 \(i\) 位,如果 \(x\) 第 \(i\) 位为 \(1\),就令 \(x\gets x\oplus v_i\),把这一位上的 \(1\) 消掉。特别地,如果 \(v_i=0\),则表明这一位上的 \(1\) 消不掉,\(x\) 不能被表示出来,所以令 \(v_i\gets x\),表示将 \(x\) 插入线性基。如果最终都没插进去,说明 \(x\) 能被表示出来,不需要插入线性基。
void insert(ll x){
for(int i=N-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{a[i]=x;break;}
}
}
合并:暴力将 \(b\) 线性基中的元素插入 \(a\) 的线性基,即可得到 \(a\cup b\) 的线性基。复杂度 \(\mathcal O(\log^2 w)\)。
删除:离线 + 线段树分治 \(\mathcal O(nB\log n)\)。在线做法先咕了。
三、应用
1. 本质不同子集异或和个数
即求 \(|\text{span}(a)|\)。设 \(b\) 为 \(a\) 的线性基,则 \(|\text{span}(a)|=2^{|b|}\)。
因为 \(\text{span}(b)=\text{span}(a)\) 且 \(b\) 线性无关,而我们知道,如果 \(a\) 线性无关,\(\text{span}(a)\) 中所有的向量,被 \(a\) 中向量表示出来的方案唯一。根据“在 \(\bmod 2\) 意义下”可证。
如果子集非空要特判 \(0\) 是否能被表示出来,因为 \(b\) 线性无关,如果子集非空不能表示出 \(0\),而 \(a\) 是有可能的。如果 \(a\) 本身就线性无关(检验:insert 看是否有插不进去的 \(a_i\)),则不能表示出 \(0\),答案要 \(-1\)。
2. 异或最大/小值
最大:从高到低枚举第 \(i\) 位,\(ans\gets\max(ans,ans\oplus b_i)\)。为什么?若 \(b_i\neq 0\),则 \(b_i\) 第 \(i\) 位必然为 \(1\)。如果 \(ans\) 第 \(i\) 位为 \(1\),则 \(ans\oplus b_i\) 第 \(i\) 位为 \(0\),并且之后不管怎么取都不能补上这位的 \(1\),不优;否则,\(ans\oplus b_i\) 第 \(i\) 位为 \(1\),更优。
ll query(){
ll ans=0;
for(int i=N-1;i>=0;i--) ans=max(ans,ans^a[i]);
return ans;
}
最小:输出最小的 \(b_i\),因为它不管与什么异或都会变大。还要看能否表示出 \(0\)。
3. 本质不同异或第 k 小
首先特判掉 \(0\),因为 \(b_i\) 异或出来的值没有 \(0\)。
设有值的 \(b_i\) 从低位到高位分别为 \(c_0,c_1,c_2,\cdots,c_t\)。
如果选好了 \(c_{i+1\sim t}\) 后,选 \(c_i\) 后总比不选 \(c_i\) 大,那么将 \(k\) 二进制拆分,如果 \(k\) 的第 \(i\) 位为 \(1\),就 \(ans\gets ans\oplus c_i\) 即可。
考虑重构线性基,使每一位的选择都不会影响下一位。从大到小枚举每一位 \(i\),枚举 \(j>i\),若 \(b_j\) 的第 \(i\) 位为 \(1\) 就令 \(b_j\gets b_j\oplus b_i\),最后得到的 \(b\) 仍满足线性基的性质。并且此时线性基满足,每个 \(b_i\neq 0\),其最高位的 \(1\)(第 \(i\) 位的 \(1\))在线性基中只出现一次(当然 \(b_i=0\) 的位 \(i\) 可以多次出现)。暂时称它为对角基。可以类比高斯消元把阶梯型矩阵消到最简行阶梯矩阵。
这样一来,不论 \(c_{i+1\sim t}\) 是否选择,都有 \(ans\oplus c_i>ans\),并且后来这一位无法消除,故选 \(c_i\) 总比不选 \(c_i\) 大。
//LOJ 114
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=51;
int n,q,cnt,flg;
ll x,k,a[N],b[N];
void insert(ll x){
for(int i=N-1;i>=0;i--) if(x>>i&1){
if(a[i]) x^=a[i];
else{a[i]=x;break;}
}
if(!x) flg=1;
}
ll query(ll k){
if(k>(1ll<<cnt)-1) return -1;
ll ans=0;
for(int i=0;i<cnt;i++) if(k>>i&1) ans^=b[i];
return ans;
}
signed main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%lld",&x),insert(x);
for(int i=N-1;i>=0;i--)
for(int j=i+1;j<N;j++)
if(a[j]>>i&1) a[j]^=a[i];
for(int i=0;i<N;i++) if(a[i]) b[cnt++]=a[i];
scanf("%d",&q);
while(q--) scanf("%lld",&k),printf("%lld\n",query(k-flg));
return 0;
}
模板题还有 [ABC283G] Partial Xor Enumeration。
4. 子集异或值排名
求 \(a\) 所有子集(可以为空)的异或值从小到大排序后,\(x\) 在其中第一次出现的位置。
-
结论:异或和为 \(v\) 的子集数:\(2^{|a|-|b|}\)(若 \(v\) 能被异或出来)。
证明:不在线性基中的数随便取,其“异或和 \(\oplus v\)”对应到线性基中有唯一的表示方式(基的性质)。
也就是说,一共有 \(2^{|b|}\) 种不同的异或和,每种异或和的出现次数都是 \(2^{|a|-|b|}\)。
转化为求所有异或值去重后,\(x\) 第一次出现的位置。
求出 \(a\) 的对角基 \(b\)。如果 \(x\) 第 \(i\) 位为 \(1\),那肯定要选 \(b_i\)。
由于只要计算排名,那么只要知道这些要选的 \(b_i\) 的 \(i\),不关心 \(b_i\) 具体的值,所以不消成对角基也没事。
//Luogu P4869
#include<bits/stdc++.h>
using namespace std;
const int N=31,mod=10086;
int n,x,k,a[N],b[N],cnt,ans;
int qpow(int x,int n){
int ans=1;
for(;n;n>>=1,x=1ll*x*x%mod) if(n&1) ans=1ll*ans*x%mod;
return ans;
}
void insert(int x){
for(int i=N-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{a[i]=x;break;}
}
}
signed main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&x),insert(x);
scanf("%d",&k);
for(int i=0;i<N;i++) if(a[i]) b[++cnt]=i;
for(int i=1;i<=cnt;i++)
if((k>>b[i])&1) ans=(ans+(1<<(i-1)))%mod;
printf("%lld\n",(1ll*ans*qpow(2,n-cnt)%mod+1)%mod);
return 0;
}
四、例题
P3265 [JLOI2015]装备购买
给出 \(n\) 个 \(m\) 维向量,每个向量有一个代价,求最多可以选多少个线性无关的向量,以及极大线性无关组的代价和最小是多少。
\(1\leq n,m\leq 500\),\(0\leq a_{i,j}\leq 10^3\)。
将线性基扩展到实数域。
将所有向量按代价从小到大排序,动态地维护 \(b\),插入一个 \(a_i\) 时,查看其是否可以表示为 \(b\) 中的线性组合,如果可以则不插入,否则将其插入 \(b\),答案加上其代价。正确性同 Kruskal。
#include<bits/stdc++.h>
using namespace std;
const int N=510;
int n,m,c[N],id[N],b[N],cnt,ans;
double eps=1e-5,a[N][N];
void insert(int x){
for(int i=1;i<=m;i++) if(fabs(a[x][i])>eps){
if(!b[i]){b[i]=x,cnt++,ans+=c[x]; break;}
else{
double t=a[x][i]/a[b[i]][i];
for(int j=i;j<=m;j++) a[x][j]-=a[b[i]][j]*t;
}
}
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) scanf("%lf",&a[i][j]);
for(int i=1;i<=n;i++)
scanf("%d",&c[i]),id[i]=i;
sort(id+1,id+1+n,[](int x,int y){return c[x]<c[y];});
for(int i=1;i<=n;i++) insert(id[i]);
printf("%d %d\n",cnt,ans);
return 0;
}
P4839 P哥的桶
有一个长度为 \(n\) 的序列 \(a\),每个 \(a_i\) 都是一个集合。\(m\) 次操作:
1 x v:将 \(v\) 放入集合 \(a_x\)。2 l r:询问 \(a_{l\sim r}\) 能构造出的异或最大值。\(n,m\leq 5\times 10^4\),\(v<2^{31}\)。
线段树,每个节点维护其代表区间的线性基。单点修改就将 \(v\) 插入根到叶子节点路径上每个节点的线性基中,区间查询就执行 \(\log n\) 次线性基合并。
时间复杂度 \(\mathcal O(m\log n\log^2 w)\)。
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+5,M=31;
int n,m,op,x,y,res;
struct node{
int a[M];
void insert(int x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{a[i]=x;break;}
}
}
}s[N<<2],ans;
void modify(int p,int l,int r,int pos,int v){
s[p].insert(v);
if(l==r) return ;
int mid=(l+r)/2;
if(pos<=mid) modify(p<<1,l,mid,pos,v);
else modify(p<<1|1,mid+1,r,pos,v);
}
void query(int p,int l,int r,int lx,int rx){
if(l>=lx&&r<=rx){
for(int i=0;i<M;i++) if(s[p].a[i]) ans.insert(s[p].a[i]);
return ;
}
int mid=(l+r)/2;
if(lx<=mid) query(p<<1,l,mid,lx,rx);
if(rx>mid) query(p<<1|1,mid+1,r,lx,rx);
}
signed main(){
scanf("%d%d",&m,&n);
while(m--){
scanf("%d%d%d",&op,&x,&y);
if(op==1) modify(1,1,n,x,y);
else{
fill(ans.a,ans.a+M,0),query(1,1,n,x,y),res=0;
for(int i=M-1;i>=0;i--) res=max(res,res^ans.a[i]);
printf("%d\n",res);
}
}
return 0;
}
CF1100F Ivan and Burgers(*2500)
给出一个长度为 \(n\) 的序列 \(a\),\(q\) 次询问,每次给定 \(l,r\),要求在 \(a_l,a_{l+1},\cdots,a_r\) 中选取任意个,使得它们的异或和最大。
\(1\leq n,q\leq 5\times 10^5\),\(0\leq a_i\leq 10^6\)。
类似上一题线段树 + 线性基,3log 过不去。
考虑对每个前缀 \(a_1,a_2,\cdots,a_i\) 各建一个线性基,额外维护一个 \(pos_i\) 表示能够使这一位为 \(1\) 的最大的位置,那么 \([l,r]\) 的线性基就是前缀 \([1,r]\) 的线性基中 \(pos_i\geq l\) 的部分。
每插入一个值 \(x=a_p\),如果 \(x\) 第 \(i\) 位为 \(1\) 且 \(pos_i<p\),就把 \(b_i\) 换成 \(x\),\(pos_i\) 换成 \(p\)(swap(b[i],x),swap(pos[i],p)),然后把交换后的 \(x,p\) 继续往下插入,这样构造出的线性基 \(pos\) 就是最大的了。
时间复杂度 \(\mathcal O(n\log n)\)。
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,M=25;
int n,m,x,l,r;
struct node{
int a[M],pos[M];
void insert(int x,int p){
for(int i=20;i>=0;i--) if((x>>i)&1){
if(!a[i]){a[i]=x,pos[i]=p;break;}
else if(pos[i]<p) swap(a[i],x),swap(pos[i],p);
x^=a[i];
}
}
int query(int l){
int ans=0;
for(int i=20;i>=0;i--)
if(pos[i]>=l) ans=max(ans,ans^a[i]);
return ans;
}
}pre[N];
signed main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&x),pre[i]=pre[i-1],pre[i].insert(x,i);
scanf("%d",&m);
while(m--) scanf("%d%d",&l,&r),printf("%d\n",pre[r].query(l));
return 0;
}
ABC223H 也用到了这个技巧。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=4e5+5,M=65;
int n,m,l,r;
ll x;
struct node{
ll a[M]; int pos[M];
void insert(ll x,int p){
for(int i=60;i>=0;i--) if((x>>i)&1){
if(!a[i]){a[i]=x,pos[i]=p;break;}
else if(pos[i]<p) swap(a[i],x),swap(pos[i],p);
x^=a[i];
}
}
bool ok(int l,ll x){
for(int i=60;i>=0;i--) if((x>>i)&1){
if(!a[i]||pos[i]<l) return 0;
else x^=a[i];
}
return 1;
}
}pre[N];
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%lld",&x),pre[i]=pre[i-1],pre[i].insert(x,i);
while(m--){
scanf("%d%d%lld",&l,&r,&x);
puts(pre[r].ok(l,x)?"Yes":"No");
}
return 0;
}
P3292 [SCOI2016]幸运数字
给出一棵 \(n\) 个点的树,\(q\) 次询问 \(x\to y\) 的简单路径上,任意选择若干个点的点权异或和的最大值。
\(n\leq 2\times 10^4\),\(q\leq 2\times 10^5\),\(a_i\leq 2^{60}\)。
线段树 + 树剖 + 线性基,复杂度 4log 甚至跑不过暴力。
考虑倍增,设 \(f_{i,j}\) 表示 \(i\) 的 \(2^j\) 级祖先,\(g_{i,j}\) 表示 \(i\to f_{i,j}\) 的点权的线性基。\(f_{i,j}=f_{f_{i,j-1},j-1}\),\(g_{i,j}=g_{i,j-1}\text{ merge }g_{f_{i,j-1},j-1}\)。
如果暴力跳父亲合并线性基,要进行 \(\log n\) 次线性基合并,复杂度 \(\mathcal O((n+m)\log^3 n)\),还是无法通过。
注意到插入 \(x\) 后,再重新插入 \(x\),线性基不变,也就是线性基合并可重复计算贡献的量。那么类似 ST 表,设 \(t=\text{lca}(x,y)\),\(k=\lfloor\log_2(dep_x-dep_t+1)\rfloor\),我们只需将 \(g_{x,k}\) 与 \(g_{\text{jump}(x,dep_x-dep_t+1-2^k),k}\) 合并即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e4+5,M=61;
int n,q,x,y,f[N][21],d[N],t,k;
ll a[N],res;
vector<int>v[N];
struct node{
ll a[M];
void insert(ll x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{a[i]=x;break;}
}
}
friend node operator+(node x,node y){
for(int i=0;i<M;i++)
if(y.a[i]) x.insert(y.a[i]);
return x;
}
}g[N][25],ans;
void dfs(int x,int fa){
g[x][0].insert(a[x]);
for(int i=0;i<=19;i++)
f[x][i+1]=f[f[x][i]][i],g[x][i+1]=g[x][i]+g[f[x][i]][i];
for(int y:v[x])
if(y!=fa) f[y][0]=x,d[y]=d[x]+1,dfs(y,x);
}
int lca(int x,int y){
if(d[x]<d[y]) swap(x,y);
for(int i=20;i>=0;i--) if(d[f[x][i]]>=d[y]) x=f[x][i];
if(x==y) return x;
for(int i=20;i>=0;i--)
if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
signed main(){
scanf("%d%d",&n,&q);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<n;i++)
scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
dfs(1,0);
while(q--){
scanf("%d%d",&x,&y),t=lca(x,y),res=0;
auto get=[&](int x,int k){
for(int i=20;i>=0;i--) if((k>>i)&1) x=f[x][i];
return x;
};
k=log2(d[x]-d[t]+1),ans=g[x][k]+g[get(x,d[x]-d[t]+1-(1<<k))][k];
k=log2(d[y]-d[t]+1),ans=ans+g[y][k]+g[get(y,d[y]-d[t]+1-(1<<k))][k];
for(int i=M-1;i>=0;i--) res=max(res,res^ans.a[i]);
printf("%lld\n",res);
}
return 0;
}
P5607 [Ynoi2013] 无力回天 NOI2017
给出一个长度为 \(n\) 的序列 \(a\),\(m\) 次操作:
1 l r v:\(\forall i\in[l,r],a_i\gets a_i\oplus v\)。2 l r v:查询 \([l,r]\) 内选任意个数(包括 \(0\) 个)xor 起来,这个值与 \(v\) 的最大 xor 和。\(1\leq n,m\leq 5\times 10^4\),值域 \([0,10^9]\)。
线性基 + 线段树。可如果区间修改打标记,会出现问题:线性基不支持整体加,即 \(a_1,a_2,\cdots,a_n\) 的线性基 \(\neq\) \(a_1\oplus v,a_2\oplus v,\cdots,a_n\oplus v\) 的线性基。
于是考虑差分,记 \(b_i=a_i\oplus a_{i-1}\),将区间异或转化为单点异或 \(b_l,b_{r+1}\)。
因为 \(\forall i\in[l,r],a_i=a_l\oplus(\text{xor}_{l+1}^ib_j)\),如果某个数能用 \(a_l,a_{l+1},\cdots,a_r\) 表示,那肯定也能用 \(a_l,b_{l+1},\cdots,b_r\) 表示,反之亦然,所以 \(a_l,a_{l+1},\cdots,a_r\) 的线性基就是 \(a_l,b_{l+1},\cdots,b_r\) 的线性基。
而 \(b_{l+1},b_{l+2},\cdots,b_r\) 的线性基显然可以线段树维护,复杂度 3log。
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+5,M=30;
int n,m,a[N],op,l,r,x;
struct node{
int v,a[M];
void insert(int x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{a[i]=x;break;}
}
}
friend node operator+(node x,node y){
for(int i=0;i<M;i++) if(y.a[i]) x.insert(y.a[i]);
return x.v^=y.v,x;
}
}s[N<<2],ans;
void modify(int p,int l,int r,int pos,int v){
if(l==r){fill(s[p].a,s[p].a+M,0),s[p].insert(s[p].v^=v);return ;}
int mid=(l+r)/2;
if(pos<=mid) modify(p<<1,l,mid,pos,v);
else modify(p<<1|1,mid+1,r,pos,v);
s[p]=s[p<<1]+s[p<<1|1];
}
int calc(int p,int l,int r,int pos){
if(l==r) return s[p].v;
int mid=(l+r)/2;
if(pos<=mid) return calc(p<<1,l,mid,pos);
return s[p<<1].v^calc(p<<1|1,mid+1,r,pos);
}
void query(int p,int l,int r,int lx,int rx){
if(l>=lx&&r<=rx){ans=ans+s[p];return ;}
int mid=(l+r)/2;
if(lx<=mid) query(p<<1,l,mid,lx,rx);
if(rx>mid) query(p<<1|1,mid+1,r,lx,rx);
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=n;i>=1;i--) a[i]^=a[i-1],modify(1,1,n,i,a[i]);
while(m--){
scanf("%d%d%d%d",&op,&l,&r,&x);
if(op==1) modify(1,1,n,l,x),r<n?modify(1,1,n,r+1,x):void();
else{
fill(ans.a,ans.a+M,0),ans.insert(calc(1,1,n,l)),query(1,1,n,l+1,r);
for(int i=M-1;i>=0;i--) x=max(x,x^ans.a[i]);
printf("%d\n",x);
}
}
return 0;
}
类似的题:CF587E Duff as a Queen(*2900)。
CF959F Mahmoud and Ehab and yet another xor task(*2400)
给出一个长度为 \(n\) 的序列 \(a\),\(m\) 次询问前 \(l\) 个数中,有多少子序列的异或和为 \(x\)。
\(1\leq n,q\leq 10^5\),\(0\leq a_i<2^{30}\)。
对 \(a\) 的每个前缀 \(a_1,a_2,\cdots,a_i\) 建线性基 \(b_i\),每次询问判断 \(x\) 能否被 \(b_l\) 表示,如果不能 \(ans=0\),否则 \(ans=2^{l-|b_l|}\)。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=30,mod=1e9+7;
int n,q,p[N],x,v;
struct node{
int a[M],cnt;
void insert(int x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{a[i]=x,cnt++;break;}
}
}
bool in(int x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else return 0;
}
return 1;
}
}pre[N];
signed main(){
scanf("%d%d",&n,&q),p[0]=1;
for(int i=1;i<=n;i++)
scanf("%d",&x),pre[i]=pre[i-1],pre[i].insert(x),p[i]=2ll*p[i-1]%mod;
while(q--){
scanf("%d%d",&x,&v);
printf("%d\n",!pre[x].in(v)?0:p[x-pre[x].cnt]);
}
return 0;
}
P4151 [WC2011]最大XOR和路径
给出一张 \(n\) 个点 \(m\) 条边的无向图,边有边权,求 \(1\to n\) 的路径的最大异或和。
可能还有重边或自环,保证图连通。路径可以重复经过某些点或边,当一条边在路径中出现了多次时,其权值在计算异或和时也要被计算相应多的次数。
\(n\leq 5\times 10^4\),\(m\leq 10^5\),\(w_i\leq 10^{18}\)。
一条 \(1\to n\) 的链,可以通过走若干个环(走到环上任意一点 \(x\),走完整个环,再原路返回,往返的路径异或相抵消,只剩下新走的环),使答案异或上环的权值。
考虑随便找一棵以 \(1\) 为根的生成树,对于每条非树边 \((x,y)\),显然其与生成树上 \(x\to y\) 的路径所经过的边会形成一个环,将这个环的权值插入线性基即可。
最后随便找一条 \(1\to n\) 的链,设其权值为 \(w\),在线性基中查询与 \(w\) 异或值最大的子集即可。因为两条 \(1\to n\) 的链可以组成一个大环,这个环的权值与 \(w\) 相异或可以得到另一条链的权值。
时间复杂度 \(\mathcal O(n\log w)\)。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5,M=60;
int n,m,x,y,vis[N];
ll z,a[M],d[N];
vector<pair<int,ll> >v[N];
void insert(ll x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{a[i]=x;break;}
}
}
ll query(ll x){
for(int i=M-1;i>=0;i--) x=max(x,x^a[i]);
return x;
}
void dfs(int x){
vis[x]=1;
for(auto p:v[x]){
int y=p.first; ll z=p.second;
if(!vis[y]) d[y]=d[x]^z,dfs(y);
else insert(d[x]^d[y]^z);
}
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d%lld",&x,&y,&z),v[x].push_back({y,z}),v[y].push_back({x,z});
dfs(1);
printf("%lld\n",query(d[n]));
return 0;
}
双倍经验:CF845G Shortest Path Problem?。
CF938G Shortest Path Queries(*2900)
给出一张 \(n\) 个点 \(m\) 条边的无向图,边有边权。\(q\) 次操作:
1 x y z:加入一条边 \((x,y,z)\)。2 x y:删除边 \((x,y)\)。3 x y:询问 \(x\to y\) 的异或最短路。保证无重边、自环,图连通,且操作均合法。
\(1\leq n,m,q\leq 2\times 10^5\),\(0\leq z<2^{30}\)。
上一题的带修版本。
考虑线段树分治,对时间轴建一棵线段树,将每条边存活拆成 \(\log n\) 个小区间插入线段树。
对线段树进行 dfs,可撤销并查集维护连通性,dfs 到某个节点就将它上面的每条边 \((x,y)\) merge 起来,如果它们本来就连通说明会形成一个环,将环的权值插入线性基(并查集额外维护,点到其所在连通块代表点,路径上的权值异或和)。
时间复杂度 \(\mathcal O(n\log^2 n)\)。
#include<bits/stdc++.h>
#define pi pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=2e5+5,M=30;
int n,m,t,f[N],w[N],sz[N],op,x,y,z,top;
map<pi,pi>mp;
pair<pi,int>s[N];
struct qry{int x,y,z;}q[N];
vector<qry>v[N<<2];
struct node{
int a[M];
void insert(int x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{a[i]=x;break;}
}
}
int query(int x){
for(int i=M-1;i>=0;i--) x=min(x,x^a[i]);
return x;
}
}cur;
pi find(int x){
int d=0;
while(x!=f[x]) d^=w[x],x=f[x];
return {x,d};
}
void modify(int p,int l,int r,int lx,int rx,qry k){
if(l>=lx&&r<=rx){v[p].push_back(k);return ;}
int mid=(l+r)/2;
if(lx<=mid) modify(p<<1,l,mid,lx,rx,k);
if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,k);
}
void dfs(int p,int l,int r){
int x=top,mid=(l+r)/2;
node tmp=cur;
for(auto i:v[p]){
pi x=find(i.x),y=find(i.y);
if(x.fi==y.fi){cur.insert(x.se^y.se^i.z);continue;}
if(sz[x.fi]<sz[y.fi]) swap(x,y);
s[++top]={{x.fi,y.fi},sz[x.fi]};
f[y.fi]=x.fi,sz[x.fi]+=sz[y.fi],w[y.fi]=x.se^y.se^i.z;
}
if(l==r) q[l].x?printf("%d\n",cur.query(find(q[l].x).se^find(q[l].y).se)):0;
else dfs(p<<1,l,mid),dfs(p<<1|1,mid+1,r);
cur=tmp;
while(top>x){
int x=s[top].fi.fi,y=s[top].fi.se;
f[y]=y,w[y]=0,sz[x]=s[top].se,top--;
}
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) f[i]=i,sz[i]=1;
for(int i=1;i<=m;i++)
scanf("%d%d%d",&x,&y,&z),mp[{x,y}]={z,0};
scanf("%d",&t);
for(int i=1;i<=t;i++){
scanf("%d%d%d",&op,&x,&y);
if(op==1) scanf("%d",&z),mp[{x,y}]={z,i};
else if(op==2) modify(1,0,t,mp[{x,y}].se,i-1,{x,y,mp[{x,y}].fi}),mp.erase({x,y});
else q[i]={x,y,0};
}
for(auto p:mp){
auto e=p.fi,i=p.se;
modify(1,0,t,i.se,t,{e.fi,e.se,i.fi});
}
dfs(1,0,t);
return 0;
}
P3733 [HAOI2017]八纵八横
给出一张 \(n\) 个点 \(m\) 条边的无向图,\(q\) 次操作:
Add x y z:加入一条边 \((x,y,z)\)。Cancel k:删除第 \(k\) 次Add操作加入的边,保证该边存在。Change k z:将第 \(k\) 次Add操作的边的边权改为 \(z\),保证该边存在。求每次操作后,及没有操作前,从 \(1\) 出发最后走回 \(1\),路径边权异或和最大值,以二进制的形式给出。可以重复经过点或边,重复经过的边重复算。
有重边有自环。
\(n,m\leq 500\),\(q\leq 10^3\),\(z\leq 2^{1000}\)。
问题可以转化为求所有环的最大异或和,因为可以从 \(1\) 走到环上绕一圈,再原路返回。
线段树分治 + bitset + 线性基 即可。
#include<bits/stdc++.h>
#define ll bitset<N>
using namespace std;
const int N=1e3+5;
int n,m,q,len,x,y,cnt,id,pos[N],vis[N];
char s[N];
ll z,d[N];
vector<pair<int,ll> >g[N];
struct E{int x,y,l,r; ll z;}e[N<<1];
vector<int>v[N<<2];
struct node{
ll a[N];
void insert(ll x){
for(int i=N-1;i>=0;i--) if(x[i]){
if(a[i].any()) x^=a[i];
else{a[i]=x;break;}
}
}
ll query(){
ll x; x.reset();
for(int i=N-1;i>=0;i--) if(!x[i]) x^=a[i];
return x;
}
}cur;
void read(ll &x){
scanf("%s",s+1),len=strlen(s+1),x.reset();
for(int i=1;i<=len;i++) x[len-i]=s[i]-'0';
}
void dfs0(int x){
vis[x]=1;
for(auto p:g[x]){
int y=p.first; ll z=p.second;
if(!vis[y]) d[y]=d[x]^z,dfs0(y);
else e[++cnt]={x,y,0,q,z};
}
}
void modify(int p,int l,int r,int lx,int rx,int k){
if(l>=lx&&r<=rx){v[p].push_back(k);return ;}
int mid=(l+r)/2;
if(lx<=mid) modify(p<<1,l,mid,lx,rx,k);
if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,k);
}
void dfs(int p,int l,int r){
node tmp=cur;
int mid=(l+r)/2;
for(int i:v[p]) cur.insert(d[e[i].x]^d[e[i].y]^e[i].z);
if(l==r){
ll x=cur.query();
int i=N-1; while(!x[i]) i--;
while(~i) putchar(x[i--]+'0'); puts("");
}
else dfs(p<<1,l,mid),dfs(p<<1|1,mid+1,r);
cur=tmp;
}
signed main(){
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y),read(z);
g[x].push_back({y,z}),g[y].push_back({x,z});
}
dfs0(1);
for(int i=1;i<=q;i++){
scanf("%s%d",s+1,&x);
if(s[1]=='A') scanf("%d",&y),read(z),e[pos[++id]=++cnt]={x,y,i,q,z};
else if(s[2]=='a') e[pos[x]].r=i-1;
else{
read(z),e[pos[x]].r=i-1;
e[++cnt]={e[pos[x]].x,e[pos[x]].y,i,q,z},pos[x]=cnt;
}
}
for(int i=1;i<=cnt;i++) modify(1,0,q,e[i].l,e[i].r,i);
dfs(1,0,q);
return 0;
}
CF724G Xor-matic Number of the Graph(*2600)
给出一张 \(n\) 个点 \(m\) 条边的无向图,边有边权。
定义三元组 \((x,y,z)\,(1\leq x<y\leq n)\) 合法当且仅当存在 \(x\to y\) 的路径,边权异或和为 \(z\)。经过多次的边要计算多次。
求所有合法三元组的 \(z\) 之和对 \(10^9+7\) 取模。
\(1\leq n\leq 10^5\),\(0\leq m\leq 2\times 10^5\),\(0\leq w_i\leq 10^{18}\)。
图可能不连通,要对每个连通块分别计算。
类似 P4151 求出任意一棵 dfs 树,记录 \(x\) 到根的边权异或和 \(d_x\),把所有简单环的异或和丢到线性基里。那么 \(x\to y\) 的本质不同的异或和都可以写成 \(d_x\oplus d_y\oplus v\) 的形式,其中 \(v\) 表示线性基向量的线性组合。
肯定不能枚举 \(x,y\),考虑对于每个二进制位 \(p\),计算有多少 \(x,y,S\) 满足 \(d_x\oplus d_y\oplus \text{xor}_{v\in S}v\) 的第 \(p\) 位为 \(1\),产生 \(2^p\) \(\times\) 个数 的贡献。
设线性基为 \(b_1,b_2,\cdots,b_m\)。
- 如果 \(\exists i\) 满足 \(b_i\) 的第 \(p\) 位为 \(1\),那么不管剩下 \(m-1\) 个数选不选,我们总可以控制 \(b_i\) 的选/不选来使第 \(p\) 位为 \(1\)。故符合条件的 \((x,y,S)\) 的个数为 \(2^{m-1}\times \large\binom n 2\)。
- 否则 \(\forall S\),\(\text{xor}_{v\in S}v\) 的第 \(p\) 位为 \(0\),\((x,y,S)\) 符合条件当且仅当 \(d_x,d_y\) 的第 \(p\) 位不同,开个桶 \(num_p\) 表示有多少 \(d_x\) 第 \(p\) 位为 \(1\),贡献 \(2^m\times num_p\times (sz-num_p)\),其中 \(sz\) 为连通块大小。
时间复杂度 \(\mathcal O(n\log^2 v)\)。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5,M=61,mod=1e9+7;
int n,m,x,y,vis[N],cnt,num[M],sz,ans;
ll z,d[N],a[M];
vector<pair<int,ll> >v[N];
void insert(ll x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{cnt++,a[i]=x;break;}
}
}
void dfs(int x){
vis[x]=1,sz++;
for(int i=0;i<M;i++) num[i]+=(d[x]>>i)&1;
for(auto p:v[x]){
int y=p.first; ll z=p.second;
if(!vis[y]) d[y]=d[x]^z,dfs(y);
else insert(d[x]^d[y]^z);
}
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
scanf("%d%d%lld",&x,&y,&z);
v[x].push_back({y,z}),v[y].push_back({x,z});
}
for(int x=1;x<=n;x++) if(!vis[x]){
for(int i=0;i<M;i++) a[i]=num[i]=0;
cnt=sz=0,dfs(x);
for(int i=0;i<M;i++){
bool flg=0;
for(int j=0;j<M;j++) flg|=(a[j]>>i)&1;
if(flg) ans=(ans+(1ll<<i)%mod*((1ll<<(cnt-1))%mod)%mod*sz%mod*(sz-1)%mod*((mod+1)/2)%mod)%mod;
else ans=(ans+(1ll<<i)%mod*((1ll<<cnt)%mod)%mod*num[i]%mod*(sz-num[i])%mod)%mod;
}
}
printf("%d\n",ans);
return 0;
}
P5556 圣剑护符
给出一棵 \(n\) 个节点的树,第 \(i\) 个点的点权为 \(a_i\),\(m\) 次操作:
Update x y z:将 \(x\to y\) 简单路径上的 \(a_i\) 异或上 \(z\)。Query x y:判断对于 \(x\to y\) 简单路径上的 \(a_i\),是否存在两个不相等的子集,使得两个子集的异或和相同。\(1\leq n,q\leq 10^5\),\(0\leq a_i,z<2^{30}\)。
等价于求 \(x\to y\) 路径上的 \(a_i\) 是否线性有关。
树剖 + 线段树 + 线性基,4log 过不去。
注意到,如果集合大小 > 向量位数,则该集合一定不是线性无关集。所以如果 \(x,y\) 路径上的点数 \(>30\),输出 YES,否则暴力跳 fa 将权值插入线性基即可,修改可用树剖维护,时间复杂度 \(\mathcal O(n\log n\log v)\)。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=30;
int n,m,x,y,v,a[N],b[M],sz[N],f[N],dep[N],son[N],top[N],tot,id[N],c[N],ans;
char s[8];
vector<int>g[N];
void insert(int x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(b[i]) x^=b[i];
else{b[i]=x;return ;}
}
ans=1;
}
void dfs(int x){
sz[x]=1;
for(int y:g[x])
if(y!=f[x]) f[y]=x,dep[y]=dep[x]+1,dfs(y),sz[x]+=sz[y],son[x]=(sz[y]>sz[son[x]]?y:son[x]);
}
void dfs2(int x,int tp){
id[x]=++tot,top[x]=tp;
if(son[x]) dfs2(son[x],tp);
for(int y:g[x])
if(y!=f[x]&&y!=son[x]) dfs2(y,y);
}
void upd(int x,int y,int k){
auto add=[&](int x,int y){
for(int i=x;i<=n;i+=i&(-i)) c[i]^=y;
};
add(x,k),add(y+1,k);
}
int query(int x){
int ans=0;
for(int i=x;i;i-=i&(-i)) ans^=c[i];
return ans;
}
int lca(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
x=f[top[x]];
}
return dep[x]<dep[y]?x:y;
}
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<n;i++)
scanf("%d%d",&x,&y),g[x].push_back(y),g[y].push_back(x);
dfs(1),dfs2(1,1);
while(m--){
scanf("%s%d%d",s+1,&x,&y);
if(s[1]=='U'){
scanf("%d",&v);
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) swap(x,y);
upd(id[top[x]],id[x],v),x=f[top[x]];
}
if(dep[x]>dep[y]) swap(x,y);
upd(id[x],id[y],v);
}
else{
int z=lca(x,y);
if(dep[x]+dep[y]-dep[z]*2>30){puts("YES");continue;}
fill(b,b+M,0),ans=0;
while(dep[x]>dep[z]) insert(a[x]^query(id[x])),x=f[x];
while(dep[y]>dep[z]) insert(a[y]^query(id[y])),y=f[y];
insert(a[z]^query(id[z])),puts(ans?"YES":"NO");
}
}
return 0;
}
CF895C Square Subsets(*2000)
给出一个长度为 \(n\) 的序列 \(a\),求有多少非空子集的乘积是完全平方数。对 \(10^9+7\) 取模。
\(1\leq n\leq 10^5\),\(1\leq a_i\leq 70\)。
质因数分解后,如果每个质数的次数加起来都是偶数,说明是完全平方数。用二进制每一位的 \(0/1\) 表示每个质数次数奇偶性,这又等价于异或和每一位为 \(0\)。
求出线性基 \(b\),则答案为 \(2^{n-|b|}-1\)。
#include<bits/stdc++.h>
using namespace std;
const int N=75,M=20,mod=1e9+7;
int n,x,cnt,p[N],vis[N],v,m,a[M];
int qpow(int x,int n){
int ans=1;
for(;n;n>>=1,x=1ll*x*x%mod)
if(n&1) ans=1ll*ans*x%mod;
return ans;
}
void insert(int x){
for(int i=M-1;i>=0;i--) if((x>>i)&1){
if(a[i]) x^=a[i];
else{a[i]=x,m++;break;}
}
}
signed main(){
scanf("%d",&n);
for(int i=2;i<=70;i++) if(!vis[i]){
p[++cnt]=i;
for(int j=i;j<=70;j+=i) vis[j]=1;
}
for(int i=1;i<=n;i++){
scanf("%d",&x),v=0;
for(int j=1;j<=cnt;j++){
int c=0;
while(x%p[j]==0) x/=p[j],c^=1;
v|=c<<(j-1);
}
insert(v);
}
printf("%d\n",(qpow(2,n-m)-1+mod)%mod);
return 0;
}
P7451 [THUSCH2017] 杜老师
类似的题有 ZR#880. 小K与作品
给出 \(l,r\),求 \(l\sim r\) 这 \(r-l+1\) 个数中能选出多少个不同的子集,使得子集中数的乘积为完全平方数。特别地,空集也算一种选法,定义其乘积为 \(1\)。
对 \(998244353\) 取模。
\(T\leq 100\),\(1\leq l\leq r\leq 10^7\),\(\sum r-l+1\leq 6\times 10^7\)。
上一题的加强版。
按上一题的做法,bitset 优化异或,复杂度 \(\mathcal O(\large\frac{n\pi^2(n)}{w}\normalsize)\approx 10^{18}\),无法通过。
对于每个数,\(>\sqrt r\) 的质因子至多只有一个(不然多个乘起来就 \(>r\) 了)。考虑只对 \(1\sim r\) 的质数编号(\(r=10^7\) 时大约有 \(450\) 个),然后对 \(>\sqrt r\) 的质因子 \(p\) 建个 bitset,单独做和线性基一样的操作,不过线性基的规模从 \(\pi(10^7)\approx 10^6\) 缩小到 \(\pi(\sqrt{10^7})\approx 450\),复杂度 \(\mathcal O(\frac{n\pi^2(\sqrt n)}{w})\approx 10^{10}\)。
注意到当区间长度大于某个临界值时(打表发现大约是 \(2\sqrt n\)),线性基是非常容易塞满的,即 \([l,r]\) 中出现过的质因子都会以某个数的因数的形式被加入到线性基,只需统计 \([l,r]\) 质因子的数量(线性基的大小)。所以可以像根号分治一样,\(<2\sqrt n\) 跑线性基,\(>2\sqrt n\) 枚举质因子,复杂度 \(6000\times\large\frac{450^2}{64}\normalsize+6\times 10^6\approx 10^7\)。
#include<bits/stdc++.h>
#define ll bitset<M>
using namespace std;
const int N=1e7+5,M=450,mod=998244353;
int t,n=1e7,cnt,p[N/10],usd[N/10],p2[N],vis[N],id[N],mxp[N],l,r,tot,lim=3162;
ll a[M],b[N/10],tmp;
vector<int>v;
void insert(ll x){
for(int i=M-1;i>=0;i--) if(x[i]){
if(a[i].any()) x^=a[i];
else{a[i]=x,tot++;break;}
}
}
void add(int x){
int mx=mxp[x]; tmp.reset();
if(mx>=lim) x/=mx;
while(x!=1){
int p=mxp[x],c=0;
while(x%p==0) x/=p,c^=1;
tmp[id[p]]=c;
}
if(mx>=lim){
if(usd[id[mx]]) tmp^=b[id[mx]];
//若 x=mx,tmp 可能为空,所以必须 usd[id[mx]] 而不是 b[id[mx]].any()
else{b[id[mx]]=tmp,usd[id[mx]]=1,v.push_back(id[mx]),tot++;return ;}
}
insert(tmp);
}
signed main(){
scanf("%d",&t),p2[0]=1,p2[1]=2;
for(int i=2;i<=n;i++){
if(!vis[i]) p[id[i]=++cnt]=i,mxp[i]=i;
for(int j=1;j<=cnt&&i*p[j]<=n;j++){
vis[i*p[j]]=1,mxp[i*p[j]]=max(mxp[i],p[j]);
if(i%p[j]==0) break;
}
p2[i]=2ll*p2[i-1]%mod;
}
while(t--){
scanf("%d%d",&l,&r),tot=0;
if(r-l+1<=7e3){
for(int i=l;i<=r;i++) add(i);
for(int i:v) usd[i]=0,b[i].reset(); v.clear();
for(int i=0;i<M;i++) a[i].reset();
}
else{
for(int i=1;i<=cnt;i++){
if(p[i]>r) break;
if((l-1)/p[i]!=r/p[i]) tot++;
}
}
printf("%d\n",p2[r-l+1-tot]);
}
return 0;
}
一、线性基
向量相关
-
对于向量集合 \(a,b\),\(b\) 是 \(a\) 的一组基当且仅当 \(\text{span}(b)=a\) 且 \(b\) 线性无关。
其中 \(\text{span}(b)\) 表示 \(b\) 所有线性组合构成的集合,称为 \(b\) 的张成空间。
\(a\) 的基可能不止一组,但 \(|b|\) 都是一样的。
基的性质:\(a\) 中每个向量被 \(b\) 表示出来的方式唯一(否则相减可得 \(a\) 线性有关,矛盾)。
矩阵相关
-
阶梯型矩阵:第 \(i\) 行无法“控制”比 \(i\) 更高的维。
最简行阶梯型矩阵:能控制 \(i\) 的只可能是第 \(i\) 行。
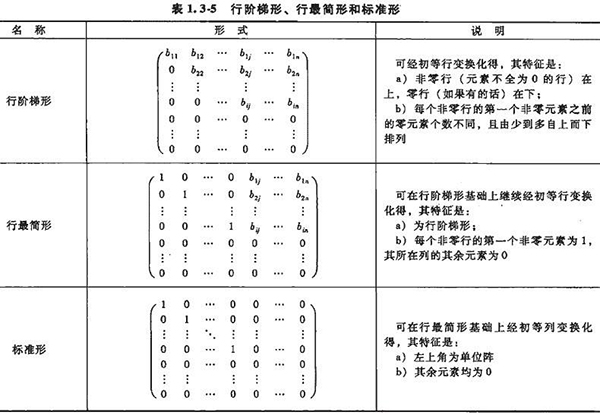
矩阵的秩:极大线性无关组的向量个数。
矩阵转置后行列式和秩都不变。
矩阵的秩 = 行向量组的秩 = 列向量组的秩。
求线性基
类比阶梯型矩阵。
-
实数线性基:
-
方法 1:高斯消元。
把向量们拼成一个矩阵。消成阶梯型矩阵后,所有非空行向量就构成了一组基(正确性:去掉一个全 \(0\) 的行向量 / 矩阵做行的初等变换 都不影响张成,而显然高斯消元后的非空行向量是线性无关的)。
称这个矩阵的秩为线性基的秩,每行的主元为线性基的主元。
时间复杂度 \(\mathcal O(nd^2)\),其中 \(d\) 为向量维数。另外,若只需要算矩阵的秩,当 \(d>n\) 时,可以转置矩阵进行 \(\mathcal O(n^2d)\) 的消元。
-
方法 2:在线插入。
\(b_i\) 表示第 \(i\) 行的向量。由于令 \(b_i\gets x\) 时 \(x\) 的更高维都是 \(0\),所以每个 \(b_i\) 的非 \(0\) 最高维都是 \(i\),维护的是阶梯型矩阵,与高斯消元本质相同。
void insert(int x){ //插入 a[x] for(int i=1;i<=m;i++) if(fabs(a[x][i])>eps){ if(!b[i]){b[i]=x;break;} else{ double t=a[x][i]/a[b[i]][i]; for(int j=i;j<=m;j++) a[x][j]-=a[b[i]][j]*t; } } }
-
-
异或线性基:把每个数看成一个 \(01\) 向量,其张成就是能异或出来的所有数。
void insert(ll x){ for(int i=60;i>=0;i--) if(x>>i&1){ if(!b[i]){b[i]=x;break;} else x^=b[i]; } }
最简线性基
类比最简行阶梯型矩阵。
-
在线插入:
void insert(ll x){ for(int i=60;i>=0;i--) if(x>>i&1){ if(!b[i]){ b[i]=x; for(int j=i-1;j>=0;j--) if(b[i]>>j&1) b[i]^=b[j]; for(int j=i+1;j<=60;j++) if(b[j]>>i&1) b[j]^=b[i]; break; } else x^=b[i]; } } -
性质:线性空间不同 \(\Leftrightarrow\) 最简线性基不同。
因为对于给定的线性空间,含有主元的子矩阵只有一种情况,非主元列也只有一种情况。
时间线性基
前缀线性基/后缀线性基。
带删除的线性基
方法 1:离线,线段树分治。
方法 2:离线,时间线性基。对每个元素预处理出它接下来要被删除的时间。用时间线性基使得线性基元素的被删除时间尽可能靠后。
方法 3:在线,带删线性基。对每个向量 bitset 维护它是由原本的哪些向量组成。
void insert(int id,int x){ //第 id 个元素 a[x]
fr[x].reset(),fr[x].set(id),pos[x]=-1;
for(int i=m-1;i>=0;i--) if(a[x].test(i)){
if(!b[i]){b[i]=x,pos[x]=i;break;}
else a[x]^=a[b[i]],fr[x]^=fr[b[i]];
}
}
void upd(int id,bitset<N>&v){ //第 id 个元素改成 v
int x=0;
for(int i=1;i<=n;i++)
if(fr[i].test(id)&&(!x||pos[i]<pos[x])) x=i;
for(int i=1;i<=n;i++)
if(fr[i].test(id)&&i!=x) a[i]^=a[x],fr[i]^=fr[x];
if(~pos[x]) b[pos[x]]=0,pos[x]=-1;
a[x]=v,insert(id,x);
}
线性基求并与求交
求并:将线性基 \(A\) 中的所有向量一个个插入到 \(B\) 中。
求交:咕咕咕
小应用
-
\(x\) 与线性基的最大异或和。
方法 1:最大子集异或和就是
qry(0)。ll qry(ll x){ for(int i=60;i>=0;i--) x=max(x,x^b[i]); return x; }方法 2:消成最简线性基,
qry(0)就是所有元素的异或和。 -
取奇数/偶数个数,使得异或和最大:给每个权值 \(+2^{61}\),根据这一位确定取了奇数个数还是偶数个数。根据需要的奇偶性,代入初始值 \(0\) 或 \(2^{61}\) 查询最大的异或和即可。
-
判 \(x\) 能否被线性基 \(b\) 表示出来:
\(b\) 为普通线性基:
insert不进去就说明能。\(b\) 未满秩时暴力insert,否则肯定能。\(b\) 为最简线性基:只需找到 \(x\) 包含的主元集合 \(S\),判断 \(\oplus_{i\in S}b_i\) 是否为 \(0\) 即可。
-
用线性基代替高斯消元。
-
序列查询区间构成的线性基:一个性质是,按顺序无论加入多少个元素,不同的最简线性基只有 \(\mathcal O(d)\) 个,因为成功插入一次秩必定 \(+1\)。扫描线 \(r\),维护以 \(r\) 为结尾的所有区间的本质不同最简线性基,时间复杂度 \(\mathcal O(nd^2)\)。
-
非空子集异或和本质不同异或第 \(k\) 小:消成最简线性基 + 二进制从高到低按位贪心。
void insert(ll x){ for(int i=60;i>=0;i--) if(x>>i&1){ if(!b[i]){ b[i]=x; for(int j=i-1;j>=0;j--) if(b[i]>>j&1) b[i]^=b[j]; for(int j=i+1;j<=60;j++) if(b[j]>>i&1) b[j]^=b[i]; break; } else x^=b[i]; } if(!x) f0=1; } ll kth(ll k){ k-=f0; if(k>(1ll<<cnt)-1) return -1; ll ans=0; for(int i=cnt-1;i>=0;i--) if(k>=(1ll<<i)) k-=1ll<<i,ans^=b[i]; //其实等价于 for(int i=0;i<cnt;i++) if(k>>i&1) ans^=b[i]; return ans; } signed main(){ scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%lld",&x),insert(x); for(int i=0;i<=60;i++) if(b[i]) b[cnt++]=b[i]; scanf("%d",&q); while(q--) scanf("%lld",&k),printf("%lld\n",kth(k)); return 0; } -
异或和为 \(v\) 的子集数:\(2^{n-|b|}\)(若 \(v\) 能被异或出来)。
因为不在线性基中的数随便取,其“异或和 \(\oplus v\)”对应到线性基中有唯一的表示方式(基的性质)。
也就是说,一共有 \(2^{|b|}\) 种不同的异或和,每种异或和的出现次数都是 \(2^{n-|b|}\)。
-
另一种理解方式是高斯消元。本质是转置起来看。
每个 \(a_i\) 对应一个 \(01\) 变量 \(x_i\) 表示是否选择。则每一位 \(k\) 对应一个方程,形如 \(\oplus_{i=1}^n x_ibit(a_i,k)=bit(v,k)\)。
(把每个 \(a_i\) 写成一行,原本是对每行看,现在对每列看)
假设有 \(t\) 位。对这 \(t\) 个 \(n\) 异或方程组做高斯消元,答案就是 \(2^{自由元个数}\)。
\[\left( \begin{matrix} bit(a_1,1)&bit(a_2,1)&\cdots&bit(a_t,1)\\ bit(a_1,2)&bit(a_2,2)&\cdots&bit(a_t,2)\\ \vdots &\vdots&\ddots&\vdots\\ bit(a_1,t)&bit(a_2,t)&\cdots&bit(a_t,t) \end{matrix} \middle| \begin{matrix} bit(v,1) \\ bit(v,2) \\ \vdots\\ bit(v,t) \end{matrix} \right) \]而自由元对应的 \(a_i\),就是不在线性基里的数,因为不管它选不选都不影响张成。
本质:矩阵的秩 = 行向量组的秩 = 列向量组的秩。
\[rank\left( \begin{matrix} bit(a_1,1)&bit(a_2,1)&\cdots&bit(a_t,1)\\ bit(a_1,2)&bit(a_2,2)&\cdots&bit(a_t,2)\\ \vdots &\vdots&\ddots&\vdots\\ bit(a_1,t)&bit(a_2,t)&\cdots&bit(a_t,t) \end{matrix} \right)=rank \left( \begin{matrix} bit(a_1,1)&bit(a_1,2)&\cdots&bit(a_1,t)\\ bit(a_2,1)&bit(a_2,2)&\cdots&bit(a_2,t)\\ \vdots &\vdots&\ddots&\vdots\\ bit(a_n,1)&bit(a_n,2)&\cdots&bit(a_t,t) \end{matrix} \right) \]
-
-
可空子集异或值和排名:
考虑最简线性基,要异或出 \(x\),那控制 \(x\) 每一位的主元对应的行都必须选。容易算出 \(x\) 在去重后的异或值中的排名。由于每种异或和的出现次数都是 \(2^{n-|b|}\),能算出 \(x\) 在未去重时的排名。
实现时,由于只关心有哪些主元,所以不需要消成最简线性基。
int rnk(ll x){ ll ans=0; for(int i=cnt-1;i>=0;i--) if(x>>b[i]&1) ans+=1ll<<i; //b 表示有哪些主元 return (ans%mod*pw[n-cnt]%mod+1)%mod; } //for(int i=0;i<=60;i++) if(b[i]) b[cnt++]=i;
k 进制线性基
线性基的本质是高斯消元。
#define vec array<int,30>
vec operator-(vec a,vec b){
for(int i=0;i<m;i++) a[i]=(a[i]-b[i]+k)%k;
return a;
}
vec operator*(vec a,int b){
for(int i=0;i<m;i++) a[i]=1ll*a[i]*b%k;
return a;
}
void insert(vec x){
for(int i=m-1;i>=0;i--) if(x[i]){
if(!b[i][i]){b[i]=x;break;}
while(x[i]) //辗转相减
b[i]=b[i]-x*(b[i][i]/x[i]),swap(b[i],x);
}
}
\(k\) 进制异或的定义是,在 \(k\) 进制下做不进位加法。
求最大/最小异或和。
下面称不进位加法为“累加”。
没法直接把 \(b\) 拿去求最大/最小异或和:一个数的累加次数不确定。比如 \(num\) 的最高位是 \(pos\),累加 \(x\) 次 \(num\) 与累加 \(y\) 次 \(num\),得到的第 \(pos\) 位都相同,但低位不一定相同。
注意到,如果累加 \(\frac{\text{lcm}(bit(num,pos),k)}{bit(num,pos)}=\frac{k}{\gcd(bit(num,pos),k)}\) 次 \(num\),那么 \(bit(num,pos)\) 不会改变。
于是类似完全背包,将 \(num\) 的 \(\frac{k}{\gcd(bit(num,pos),k)}\) 次累加值也插入线性基、参与张成即可。
void exgcd(int a,int b,int &x,int &y){
if(!b){x=1,y=0;return ;}
exgcd(b,a%b,y,x),y-=a/b*x;
}
vec query(vec x){ //最小异或和
for(int i=0;i<m;i++) insert(b[i]*(k/__gcd(b[i][i],k))); //!!!
for(int i=m-1;i>=0;i--) if(b[i][i]){
int u,v,d=__gcd(b[i][i],k);
exgcd(b[i][i],k,u,v),u=(u%k+k)%k; //u*b[i] 的第 i 位为 d
x=x-b[i]*(1ll*x[i]/d*u%k); //想使 x[i] 减 x[i]/d 次 d
}
return x;
}
QOJ#5402. 术树数:
#include<bits/stdc++.h>
#define vec array<int,30>
using namespace std;
const int N=2e5+5;
int q,n=1,k,m,op,x,y,v;
vec b[35],dis[N],ans;
vec operator+(vec a,vec b){
for(int i=0;i<m;i++) a[i]=(a[i]+b[i])%k;
return a;
}
vec operator-(vec a,vec b){
for(int i=0;i<m;i++) a[i]=(a[i]-b[i]+k)%k;
return a;
}
vec operator*(vec a,int b){
for(int i=0;i<m;i++) a[i]=1ll*a[i]*b%k;
return a;
}
vec to(int x){
vec a;
for(int i=0;i<m;i++) a[i]=x%k,x/=k;
return a;
}
void exgcd(int a,int b,int &x,int &y){
if(!b){x=1,y=0;return ;}
exgcd(b,a%b,y,x),y-=a/b*x;
}
void insert(vec x){
for(int i=m-1;i>=0;i--) if(x[i]){
if(!b[i][i]){b[i]=x;break;}
while(x[i])
b[i]=b[i]-x*(b[i][i]/x[i]),swap(b[i],x);
}
}
vec query(vec x){
for(int i=m-1;i>=0;i--) if(b[i][i]){
int u,v,d=__gcd(b[i][i],k);
exgcd(b[i][i],k,u,v),u=(u%k+k)%k;
x=x-b[i]*(1ll*x[i]/d*u%k);
}
return x;
}
signed main(){
scanf("%d%d%d",&q,&k,&m);
while(q--){
scanf("%d%d%d",&op,&x,&y);
if(op==1) dis[++n]=dis[x]+to(y),insert(to(y)+to(y));
if(op==2) scanf("%d",&v),insert(dis[x]+dis[y]+to(v));
if(op==3){
for(int i=0;i<m;i++) insert(b[i]*(k/__gcd(b[i][i],k)));
ans=query(dis[x]+dis[y]),v=0;
for(int i=m-1;i>=0;i--) v=v*k+ans[i];
printf("%d\n",v);
}
}
return 0;
}
二、例题
1. QOJ#61. Cut Cut Cut!
2023.9.19
给出一张 \(n\) 个点 \(m\) 条边的网络(DAG),每条边容量均为 \(1\),且节点 \(1\) 的出边只有 \(\leq 10\) 条。
对每个 \(x\in[2,n]\),求 \(1\leadsto x\) 的最大流。
\(n\leq 10^5\),\(m\leq 2\times 10^5\)。
设 \(1\) 的出边条数为 \(d\)。
做法:
-
给 \(1\) 的所有出边分别随机一个 \(d\) 维向量。
接下来,把每个点入边向量的随机线性组合(每个入边向量乘一个随机数再加起来)作为出边的向量。
\(ans_x\) 就是 \(x\) 所有入边向量生成的线性空间的秩。
实现时,为了避免 \(\sum indeg\times outdeg\),根据入边的线性组合随机出边时,需要消出入边的线性基,用线性基里的元素随机线性组合(因为本来就是在入边的线性空间里随机选一个向量)。
时间复杂度 \(\mathcal O(md^2)\)。
正确性:
-
割后面的边都是割的线性组合。
所以 \(x\) 的所有入边,都是最小割那些边的线性组合,因此秩一定 \(\leq\) 最小割。至于为什么不会比最小割小,是随机保证的,我也不太会证。
#include<bits/stdc++.h>
#define vec array<int,10>
using namespace std;
const int N=1e5+5,mod=998244353;
int n,m,d=10,x,y;
vector<int>v[N];
vec w;
mt19937 rnd(time(0));
vec operator+(vec a,vec b){
for(int i=0;i<d;i++) a[i]=(a[i]+b[i])%mod;
return a;
}
vec operator*(vec a,int b){
for(int i=0;i<d;i++) a[i]=1ll*a[i]*b%mod;
return a;
}
int qpow(int x,int n){
int ans=1;
for(;n;n>>=1,x=1ll*x*x%mod) if(n&1) ans=1ll*ans*x%mod;
return ans;
}
struct B{
int cnt;
vec b[15];
void insert(vec x){
for(int i=d-1;i>=0;i--) if(x[i]){
if(!b[i][i]){b[i]=x,cnt++;break;}
else x=x+b[i]*(mod-1ll*x[i]*qpow(b[i][i],mod-2)%mod);
}
}
}in[N];
signed main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d",&x,&y),v[x].push_back(y);
for(int y:v[1]){
for(int i=0;i<d;i++) w[i]=rnd();
in[y].insert(w);
}
for(int x=2;x<=n;x++){
printf("%d\n",in[x].cnt);
for(int y:v[x]){
for(int i=0;i<d;i++) w[i]=0;
for(int i=0;i<d;i++) w=w+in[x].b[i]*rnd();
in[y].insert(w);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号