「算法笔记」线段树专题

修改于 2024 年不知道哪月。

2020 年写的可持久化线段树（已折叠）

一、引入

有的时候，我们不仅需要支持修改，还需要支持访问历史版本。

这个时候普通的线段树就没法胜任了，因为每次我们都覆盖了之前的版本。

若想知道数据集在任意时间的历史状态，有没有什么方法呢？

方法一：直接记录之前得到的所有的线段树。在第 i 项操作结束后（∀i∈[1,M]），把整个线段树拷贝一遍，存储在 history[i] 中，多耗费 M 倍的空间。

复杂度 O(n²)。

方法二：注意到每次修改的位置都不会很多，所以相同的节点就没必要再记录一遍了。

复杂度 O(n log n)。

比如说要对 15 号节点进行“单点修改”，我们需要新建节点，如下图所示，白色的为最初版本的线段树，红色的为版本 2。产生了 O(logN) 个新节点。

唯一的问题是由于需要每次新建节点，我们没办法再用位运算（p<<1,p<<1|1）访问子节点，而需要在每一个点上记录左右儿子的位置。

这就是可持久化线段树（主席树）的基本思想。

二、区间第 k 小

Luogu P3834 主席树模板题

题目大意：长度为 n 的数组，每次查询一段区间里第 k 小的数。1≤n,q≤2×10⁵。

Solution：

我们先考虑一个比较简单的问题：如何维护全局第 k 小？

维护序列中落在值域区间 [L,R] 中数的个数（记作 cnt_L,R）。比较 cnt_L,mid 与 k 的大小关系，即可确定序列中第 k 小的数是 ≤mid 还是 >mid，从而可以进入线段树的左、右子树之一。换言之，可以建一棵权值线段树，然后在线段树上二分解决。 

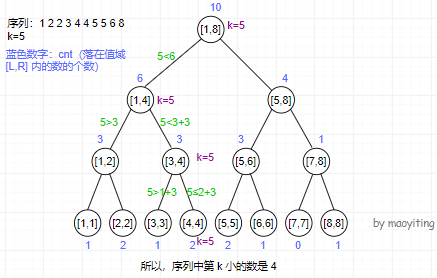
维护前缀第 k 小？

把这个权值线段树可持久化，这样我们就可以随时拎出来一个前缀。

区间第 k 小？

相当于两个线段树相减（类似前缀和？），同样可以用可持久化线段树维护。

“root[r] 的值域区间 [L,R] 的 cnt 值”-“root[l-1] 的值域区间 [L,R] 的 cnt 值”=“序列中落在值域 [L,R] 内的数的个数”，也就是可持久化线段树中两个代表相同值域的节点具有可减性。

时间复杂度 O(n log n)。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int n,m,l,r,k,tot,a[N],t,b[N],lc[N<<5],rc[N<<5],sum[N<<5],root[N];    //lc[],rc[]:左右子节点编号  tot:可持久化线段树的总点数  root[]:可持久化线段树的每个根 
void build(int &p,int l,int r){    //建出一棵初始时的的树
    p=++tot,sum[p]=0;    //新建一个节点
    if(l==r) return ;
    int mid=(l+r)/2;
    build(lc[p],l,mid);
    build(rc[p],mid+1,r);
}
int insert(int p,int l,int r,int pos,int ave){
    int x=++tot;
    lc[x]=lc[p],rc[x]=rc[p],sum[x]=sum[p];    //动态开点，先复制原来的节点 
    if(l==r){sum[x]+=ave;return x;}
    int mid=(l+r)/2;
    if(pos<=mid) lc[x]=insert(lc[p],l,mid,pos,ave);
    else rc[x]=insert(rc[p],mid+1,r,pos,ave);
    sum[x]=sum[lc[x]]+sum[rc[x]];
    return x; 
} 
int query(int x,int y,int l,int r,int k){    //在 x,y 两个节点上，值域为 [l,r]，求第 k 小的数 
    if(l==r) return l;    //找到答案 
    int mid=(l+r)/2,v=sum[lc[x]]-sum[lc[y]],ans=0;    //v:有多少个数落在值 [l,mid] 内 
    if(v>=k) ans=query(lc[x],lc[y],l,mid,k);
    else ans=query(rc[x],rc[y],mid+1,r,k-v);
    return ans;
} 
signed main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]),b[++t]=a[i];
    sort(b+1,b+1+t),t=unique(b+1,b+1+t)-b-1;    //离散化 
    build(root[0],1,t); 
    for(int i=1;i<=n;i++){
        int x=lower_bound(b+1,b+1+t,a[i])-b;
        root[i]=insert(root[i-1],1,t,x,1);    //在上一个版本的基础上修改
    }
    while(m--){
        scanf("%lld%lld%lld",&l,&r,&k);
        int x=query(root[r],root[l-1],1,t,k); 
        printf("%lld\n",b[x]);
    }
    return 0;
}

三、树上第 k 小

Luogu P2633 Count on a tree

题目大意：n 个点的一棵树，每次查询一条链 u,v 上第 k 小的数。1≤n,q≤10⁵。

Solution：

树链剖分，然后可持久化，每次拿出来 O(log n) 个线段树进行二分，……

恭喜你想到了一个 O(n log³ n) 的算法。

我们注意到，在可持久化线段树上，我们的 root[x] 不一定去依赖 root[x-1]，完全可以依赖别的位置。

所以我们可以每一个点依赖它的父节点。这样每一个点的线段树就是维护的它到根节点的信息。

对于一条链 u...v，我们设 u 和 v 的 LCA 是 d，那么只需要在 T(u)+T(v)-T(d)-T(fa(d)) 上进行二分即可。

时间复杂度 O(n log n)。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5;
int n,m,x,y,k,lastans,tot,a[N],t,b[N],lc[N<<5],rc[N<<5],sum[N<<5],root[N],cnt,hd[N],to[N<<1],nxt[N<<1],dep[N],f[N][30];
void add(int x,int y){
    to[++cnt]=y,nxt[cnt]=hd[x],hd[x]=cnt;
}
void build(int &p,int l,int r){
    p=++tot,sum[p]=0;
    if(l==r) return ;
    int mid=(l+r)/2;
    build(lc[p],l,mid);
    build(rc[p],mid+1,r);
}
int insert(int p,int l,int r,int pos,int ave){
    int x=++tot;
    lc[x]=lc[p],rc[x]=rc[p],sum[x]=sum[p];
    if(l==r){sum[x]+=ave;return x;}
    int mid=(l+r)/2;
    if(pos<=mid) lc[x]=insert(lc[p],l,mid,pos,ave);
    else rc[x]=insert(rc[p],mid+1,r,pos,ave);
    sum[x]=sum[lc[x]]+sum[rc[x]];
    return x; 
} 
int query(int a,int b,int c,int d,int l,int r,int k){
    if(l==r) return l;
    int mid=(l+r)/2,v=sum[lc[a]]+sum[lc[b]]-sum[lc[c]]-sum[lc[d]],ans=0;    //T(u)+T(v)-T(d)-T(fa(d))
    if(v>=k) ans=query(lc[a],lc[b],lc[c],lc[d],l,mid,k);
    else ans=query(rc[a],rc[b],rc[c],rc[d],mid+1,r,k-v);
    return ans;
} 
void dfs(int x,int fa){    //预处理 
    root[x]=insert(root[fa],1,t,lower_bound(b+1,b+1+t,a[x])-b,1);    //每一个点依赖它的父节点
    dep[x]=dep[fa]+1;
    for(int i=0;i<=19;i++)
        f[x][i+1]=f[f[x][i]][i];
    for(int i=hd[x];i;i=nxt[i]){
        int y=to[i];
        if(y!=fa) f[y][0]=x,dfs(y,x);
    }
}
int LCA(int x,int y){    //求 LCA 
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=20;i>=0;i--){
        if(dep[f[x][i]]>=dep[y]) x=f[x][i];
        if(x==y) return x; 
    }
    for(int i=20;i>=0;i--)
        if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    return f[x][0];
}
signed main(){
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%lld",&a[i]),b[++t]=a[i];
    for(int i=1;i<n;i++){
        scanf("%lld%lld",&x,&y);
        add(x,y),add(y,x);
    }
    sort(b+1,b+1+t),t=unique(b+1,b+1+t)-b-1;    //离散化 
    build(root[0],1,t),dfs(1,0);
    while(m--){
        scanf("%lld%lld%lld",&x,&y,&k),x^=lastans;
        int d=LCA(x,y),v=query(root[x],root[y],root[d],root[f[d][0]],1,t,k);
        printf("%lld\n",lastans=b[v]);
    }
    return 0;
}

四、可持久化并查集

并查集的基本操作：

int f[N],sz[N];    //fa、size 
int find(int x){    //查询 
    return x==f[x]?x:f[x]=find(f[x]);    //优化 1:路径压缩 
}
void merge(int x,int y){    //合并 
    x=find(x),y=find(y);
    if(x!=y){
        if(sz[x]<sz[y]) swap(x,y);
        f[y]=x,sz[x]+=sz[y]; 
    }    //优化 2:启发式合并（按秩合并） 
}

首先科普一个关于并查集的知识点：

• 按秩合并 + 路径压缩：O(α(n))（反阿克曼函数）
• 只用按秩合并或只用路径压缩：O(log n)

在某些情况下，我们只能用按秩合并不能用路径压缩，比如可持久化。

然后回归正题。

Luogu P3402 可持久化并查集模板题

题目大意：实现一个可持久化并查集，不光要支持所有并查集的操作，还需要支持访问历史版本。1≤n,q≤10⁵。

Solution：

用可持久化线段树，我们可以实现数组的可持久化。也就是维护一个数组，支持单点修改数组元素和访问历史版本。

并查集，其实无非是维护 fa 和 size，将这两个数组都可持久化，我们就可以实现并查集的可持久化。

不能路径压缩，因为那样的话 fa 会进行很多修改。

时间复杂度 O(n log² n)，两个 log n 一个来自按秩合并并查集一个来自可持久化线段树。

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int n,m,opt,x,y,tot,lc[N<<5],rc[N<<5],val[N<<5],rt[N],sz[N<<5],fa[N<<5];
void build(int &p,int l,int r){
    p=++tot;
    if(l==r){fa[p]=l,sz[p]=1;return ;}    //初始版本:父亲是它自己 fa[i]=i,sz[i]=1
    int mid=(l+r)/2;
    build(lc[p],l,mid);
    build(rc[p],mid+1,r);
}
int modify(int p,int l,int r,int pos,int v){    //把 pos 的父亲改成 v
    int x=++tot;
    lc[x]=lc[p],rc[x]=rc[p];
    if(l==r){fa[x]=v,sz[x]=sz[p],sz[v]+=sz[x];return x;}    //fa[y]=x,sz[x]+=sz[y]
    int mid=(l+r)/2;
    if(pos<=mid) lc[x]=modify(lc[p],l,mid,pos,v);
    else rc[x]=modify(rc[p],mid+1,r,pos,v);
    return x; 
} 
int query(int p,int l,int r,int pos){    //询问某一个版本的一个点的父亲
    if(l==r) return fa[p];
    int mid=(l+r)/2,ans=0;
    if(pos<=mid) ans=query(lc[p],l,mid,pos);
    else ans=query(rc[p],mid+1,r,pos);
    return ans;
} 
int find(int p,int v){
    int f=query(p,1,n,v);    //查询在版本 p 中点 v 的父亲 
    return v==f?v:find(p,f);    //无路径压缩
}
signed main(){
    scanf("%lld%lld",&n,&m);
    build(rt[0],1,n);
    for(int i=1;i<=m;i++){
        scanf("%lld",&opt);
        if(opt==1){
            scanf("%lld%lld",&x,&y);
            rt[i]=rt[i-1],x=find(rt[i],x),y=find(rt[i],y);
            if(x!=y){
                if(sz[x]<sz[y]) swap(x,y);
                rt[i]=modify(rt[i-1],1,n,y,x);    //按秩合并，小的往大的合并
            }
        }
        else if(opt==2) scanf("%lld",&x),rt[i]=rt[x];
        else{
            scanf("%lld%lld",&x,&y),rt[i]=rt[i-1];
            puts(find(rt[i],x)==find(rt[i],y)?"1":"0");
        }
    }
    return 0;
}

另外：若可以不写 build，其实可以不用写，写了反而会变慢。（有一次写了就 T 了，不写就过了 QAQ）

不知道什么时候写的标记顺序问题（已折叠）

A1

区间加，区间乘，查询区间和。

怎么处理时间顺序问题？手动钦定顺序将 \(add\) 和 \(mul\) 结合起来。

维护 tag \((mul,add)\)，考虑两条路：

1. 表示区间内的数先 \(+add\) 再 \(\times mul\)，合并 info 和 tag 就是 \(sum'\gets (sum+add\cdot len)\times mul\)。

   当前 info \(sum\) 依次经过 \((+add_x,\times mul_x),(+add_{fa},\times mul_{fa})\) 后，则会变成 \(sum'\gets ((sum+add_x\cdot len)\times mul_x+add_{fa}\cdot len)\times mul_{fa}\)，想要将外面这个 \(+add_{fa}\cdot len\times mul_{fa}\) 放进 \(add_x'\) 必须下传 \(x\) 的标记使 \(mul_x'\gets 1\) 才行，于是就要一路下传下去，复杂度就错了。

   所以这条路走不通。

2. 表示区间内的数先 \(\times mul\) 再 \(+add\)，合并 info 和 tag 就是 \(sum'\gets sum\times mul+add\cdot len\)。

   当前 info \(sum\) 依次经过 \((\times mul_x,+add_x),(\times mul_{fa},+add_{fa})\) 后，则会变成

   \[\begin{aligned} sum'&\gets(sum\times mul_x+add_x\cdot len)\times mul_{fa}+add_{fa}\cdot len\\ &=sum\times mul_x\times mul_{fa}+(add_x\times mul_{fa}+add_{fa})\cdot len \end{aligned} \]

   于是下传时 \(mul_x'\gets mul_x\times mul_{fa}\)，\(add_x'\gets add_x\times mul_{fa}+add_{fa}\)。

想想为什么 2 走的通：因为区间乘会影响区间加，但区间加不会影响区间乘，所以钦定优先级 \(mul>add\)。

A2

区间加，区间乘，区间赋值，查询区间和。

考虑区间覆盖会直接置空区间乘和区间加，区间乘会影响区间加，区间加无法影响其他操作，所以钦定优先级 \(cov>mul>add\)。

以下纯口胡。

维护 tag \((cov,mul,add)\) 表示先赋值为 \(cov\) 再 \(\times mul\) 最后 \(+add\)。若存在 \(cov\) 标记则记 \(\text{cover}(sum,cov)\) 为 \(cov\cdot len\)，否则还是 \(sum\)。那么合并 info 和 tag 就是

\[sum'\gets\text{cover}(sum,cov)\times mul+add\cdot len \]

当前 info \(sum\) 依次经过 \((cov_x,\times mul_x,+add_x),(cov_{fa},\times mul_{fa},+add_{fa})\) 后，则会变成

\[\begin{aligned} sum'&\gets \text{cover}((\text{cover}(sum,cov_x)\times mul_x+add_x\cdot len),cov_{fa})\times mul_{fa}+add_{fa}\cdot len\\ &= \begin{cases} \text{cover}(sum,cov_{fa})\times mul_{fa}+add_{fa}\cdot len&(\text{have }cov_{fa}) \\ \text{cover}(sum,cov_x)\times mul_x\times mul_{fa}+(add_x\times mul_{fa}+add_{fa})\cdot len&(\text{otherwise}) \end{cases} \end{aligned} \]

2020 年写的线段树优化建图（已折叠）

戳这里

一、线段树合并

每次合并的复杂度为两棵线段树重合的节点个数，而每遇到一个重合的节点，线段树大小之和会 \(-1\)。最开始线段树大小之和 \(\mathcal O(n\log n)\)，故重合部分、合并次数和新建节点的数量也是 \(\mathcal O(n\log n)\) 的。故复杂度 \(\mathcal O(n\log n)\)。

void merge(int &x,int y,int l,int r){
	if(!x||!y){x|=y;return ;}
	if(l==r){sum[x]+=sum[y];return ;}
	int mid=(l+r)/2;
	merge(lc[x],lc[y],l,mid);
	merge(rc[x],rc[y],mid+1,r);
	pushup(x); 
}
int merge(int x,int y,int l,int r){	//可持久化
	if(!x||!y) return x|y;
	int p=++tot,mid=(l+r)/2;
	if(l==r){sum[p]=sum[x]+sum[y];return p;}
	lc[p]=merge(lc[x],lc[y],l,mid);
	rc[p]=merge(rc[x],rc[y],mid+1,r);
	return pushup(p),p; 
} 

一般来说 merge 的时候最好加上 l,r，因为我们得知道什么时候递归到了叶子节点，从而合并叶子节点处的信息。
有两种情况不用记录 l,r：

1. 若合并的整个过程中，所有叶子节点最多在一棵线段树中出现，就可以不下传 l,r（递归到叶子时，x,y 至少有一个为空，所以直接返回了）。一个例子是线段树合并维护 SAM 的 \(\text{endpos}\) 集合，此时一个叶子结点最多在一棵线段树上有值。
2. 若可以快速合并两个有交区间的信息，不需要从子节点中合并东西上来，就不需要担心叶节点合并两个空节点作为信息。此时可以不下传 l,r。

BZOJ 4771. 七彩树

给出一棵 \(n\) 个节点的树，以 \(1\) 为根，每个点有一个颜色 \(c_i\)。\(m\) 次询问 \(x\) 子树内 \(dep\leq dep_x+d\) 的所有点中出现了多少种本质不同的颜色。

\(1\leq T\leq 500\)，\(1\leq n,m\leq 10^5\)，\(\sum n,m\leq 5\times 10^6\)，\(1\leq c_i\leq n\)，强制在线。

对每个节点用线段树 \(T_1\) 维护距离 \(\leq d\) 的子孙的颜色总数，然后线段树合并。但合并时对于新增某些颜色的情况难以维护，因为无法判定这些颜色是否出现过。

于是对每个节点用另一棵线段树 \(T_2\) 维护每个颜色 \(c\) 在其子树中所有出现位置中最浅的一个 \(mn_c\)。当合并 \(x,y\) 时，先不考虑 \(x,y\) 中颜色重复，合并它们的 \(T_1\)，然后合并它们的 \(T_2\)，如果某个颜色在 \(x,y\) 中都出现了，就在 \(T_1\) 中使 \(\max(mn_{x,c},mn_{y,c})\) 减 \(1\)。

也就是说，某个颜色对 \(T_1\) 的贡献由其最浅出现位置贡献。

时间复杂度 \(\mathcal O((n+q)\log n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,M=N<<5;
int t,n,q,x,d,c[N],ans,dep[N];
vector<int>v[N];
struct Seg1{	//需要注意合并时要新建节点，否则会破坏原有的线段树结构
	int tot,rt[N],lc[M],rc[M],sum[M];
	int modify(int p,int l,int r,int pos,int v){
		int x=++tot,mid=(l+r)/2;
		//要可持久化，不能写 if(!p) p=++tot 那种写法
		//因为 merge 后 只有一棵线段树有的节点 是共用的，在一棵线段树改了另一棵就挂了（也就是 x|=y 那里，如果 x 改了 y 也挂了）
		sum[x]=sum[p]+v;
		if(l==r) return x;
		if(pos<=mid) lc[x]=modify(lc[p],l,mid,pos,v),rc[x]=rc[p];
		else lc[x]=lc[p],rc[x]=modify(rc[p],mid+1,r,pos,v); 
		return x;
	}
	int merge(int x,int y,int l,int r){
		if(!x||!y) return x|y;
		int p=++tot,mid=(l+r)/2;
		if(l==r) return sum[p]=sum[x]+sum[y],p;	
		lc[p]=merge(lc[x],lc[y],l,mid);
		rc[p]=merge(rc[x],rc[y],mid+1,r);
		return sum[p]=sum[lc[p]]+sum[rc[p]],p;
	}
	int query(int p,int l,int r,int lx,int rx){
		if(!p) return 0;
		if(l>=lx&&r<=rx) return sum[p];
		int mid=(l+r)/2,ans=0;
		if(lx<=mid) ans=query(lc[p],l,mid,lx,rx);
		if(rx>mid) ans+=query(rc[p],mid+1,r,lx,rx);
		return ans;
	}
}t1; 
struct Seg2{
	int tot,rt[N],lc[M],rc[M],mn[M];
	void modify(int &p,int l,int r,int pos,int v){
		if(!p) p=++tot;
		if(l==r){mn[p]=v;return ;}
		int mid=(l+r)/2;
		if(pos<=mid) modify(lc[p],l,mid,pos,v);
		else modify(rc[p],mid+1,r,pos,v); 
	} 
	void merge(int &x,int y,int l,int r,int p){
		if(!x||!y){x|=y;return ;}
		if(l==r){t1.rt[p]=t1.modify(t1.rt[p],1,n,max(mn[x],mn[y]),-1),mn[x]=min(mn[x],mn[y]);return ;}
		int mid=(l+r)/2;
		merge(lc[x],lc[y],l,mid,p);
		merge(rc[x],rc[y],mid+1,r,p); 
	}
}t2;
void dfs(int x,int fa){
	dep[x]=dep[fa]+1;
	t1.rt[x]=t1.modify(t1.rt[x],1,n,dep[x],1);
	t2.modify(t2.rt[x],1,n,c[x],dep[x]);
	for(int y:v[x]) if(y!=fa){
		dfs(y,x);
		t1.rt[x]=t1.merge(t1.rt[x],t1.rt[y],1,n);
		t2.merge(t2.rt[x],t2.rt[y],1,n,x);
	}
}
signed main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&q),ans=0;
		for(int i=1;i<=t1.tot;i++) t1.lc[i]=t1.rc[i]=t1.sum[i]=0;
		for(int i=1;i<=t2.tot;i++) t2.lc[i]=t2.rc[i]=t2.mn[i]=0;
		t1.tot=t2.tot=0;
		for(int i=1;i<=n;i++)
			scanf("%d",&c[i]),v[i].clear(),t1.rt[i]=t2.rt[i]=0;
		for(int i=2;i<=n;i++)
			scanf("%d",&x),v[x].push_back(i);
		dfs(1,0);
		while(q--){
			scanf("%d%d",&x,&d),x^=ans,d^=ans;
			printf("%d\n",ans=t1.query(t1.rt[x],1,n,dep[x],dep[x]+d));
		}
	}
	return 0;
}

P5327 [ZJOI2019]语言

给出一棵 \(n\) 个节点的树，以及 \(m\) 条链 \((s_i,t_i)\)，求有多少对点至少存在一条链同时覆盖这两个点。

\(1\leq n,m\leq 10^5\)。

显然不能直接枚举点对，考虑从点开始统计，\(x\) 能到达的点，实际上是所有经过 \(x\) 的链的并集（除去 \(x\) 自己）。

因为这些链都经过同一点，所以并集是一个连通块。问题转化为，维护点集 \(S\)，支持插入、删除点（\(s_i,t_i\)），求 \(S\) 虚树中的点数 \(-1\) = 边数。

将 \(S\) 中的点按 DFS 序排序（设为 \(a_1,a_2,\cdots,a_k\)）并依次插入，插入 \(a_i\) 时虚树边数增加 \(dep_{a_i}-dep_{\text{lca}(a_i,a_{i-1})}\)。其中 \(a_0=a_k\)，相当于 \(dep_{\text{lca}(a_1,a_k)}\) 表示这个连通块的根的深度。故为 \(\sum_{x\in S}dep_x-\sum_{x,y\,\text{相邻}}dep_{\text{lca}}\)，其中相邻指 DFS 序相邻，包括首尾相邻。

树上差分拆路径，得到若干“\(u\) 在 \(S_x\) 出现次数多 \(1\) 或 \(-1\)”的操作。对每个 \(x\) 建一棵下标为 DFS 序的权值线段树，下标为 \(x\) 的位置的值表示 DFS 序为 \(x\) 的点的出现次数。每个节点维护，该节点表示的区间中，出现次数 \(>0\) 的点的 DFS 序最小值 \(mn\)、最大值 \(mx\)，以及该区间所有出现次数 \(>0\) 的节点的 \(dep\) 之和减去相邻出现次数 \(>0\) 的 \(dep_{\text{lca}}\)（不算首尾）\(sum\)。

按套路线段树合并即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=N<<6;
int n,m,x,y,t,tim,dfn[N],id[N],dep[N],f[N],sz[N],son[N],top[N],tot,rt[N],lc[M],rc[M],val[M],mn[M],mx[M],sum[M];
long long ans;
vector<int>v[N],del[N];
void dfs(int x){
	sz[x]=1,id[dfn[x]=++tim]=x;
	for(int y:v[x]) if(y!=f[x]){
		f[y]=x,dep[y]=dep[x]+1,dfs(y),sz[x]+=sz[y];
		if(sz[y]>sz[son[x]]) son[x]=y;
	} 
}
void dfs2(int x,int tp){
	top[x]=tp;
	if(son[x]) dfs2(son[x],tp);
	for(int y:v[x])
		if(y!=f[x]&&y!=son[x]) dfs2(y,y);
}
int lca(int x,int y){
	if(!x||!y) return 0;
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]]) swap(x,y);
		x=f[top[x]];
	}
	return dep[x]<dep[y]?x:y;
}
void pushup(int p){
	sum[p]=sum[lc[p]]+sum[rc[p]]-dep[lca(mx[lc[p]],mn[rc[p]])];
	mn[p]=mn[lc[p]]?mn[lc[p]]:mn[rc[p]];
	mx[p]=mx[rc[p]]?mx[rc[p]]:mx[lc[p]];
}
void modify(int &p,int l,int r,int pos,int v){
	if(!p) p=++tot;
	if(l==r){
		if(val[p]+=v) sum[p]=dep[mx[p]=mn[p]=id[l]];
		else sum[p]=mx[p]=mn[p]=0; return ;
	}
	int mid=(l+r)/2;
	if(pos<=mid) modify(lc[p],l,mid,pos,v);
	else modify(rc[p],mid+1,r,pos,v);
	pushup(p);
}
void merge(int &x,int y,int l,int r){
	if(!x||!y){x|=y;return ;}
	if(l==r){
		if(val[x]+=val[y]) sum[x]=dep[mx[x]=mn[x]=id[l]];
		else sum[x]=mx[x]=mn[x]=0; return ;
	}
	int mid=(l+r)/2;
	merge(lc[x],lc[y],l,mid);
	merge(rc[x],rc[y],mid+1,r);
	pushup(x); 
}
void dfs3(int x){
	for(int y:v[x])
		if(y!=f[x]) dfs3(y),merge(rt[x],rt[y],1,n);
	for(int i:del[x]) modify(rt[x],1,n,dfn[i],-1);
	ans+=sum[rt[x]]-dep[lca(mn[rt[x]],mx[rt[x]])]; 
}
signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<n;i++)
		scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
	dfs(1),dfs2(1,1);
	while(m--){
		scanf("%d%d",&x,&y),t=lca(x,y);
		modify(rt[x],1,n,dfn[x],1),modify(rt[x],1,n,dfn[y],1);
		modify(rt[y],1,n,dfn[x],1),modify(rt[y],1,n,dfn[y],1);
		del[t].push_back(x),del[t].push_back(y);
		del[f[t]].push_back(x),del[f[t]].push_back(y);
	}
	dfs3(1),printf("%lld\n",ans/2);
	return 0;
} 

P5298 [PKUWC2018]Minimax

线段树合并优化 DP

给出一棵 \(n\) 个节点的二叉树，定义节点 \(x\) 的权值为：

• 若 \(x\) 是叶子节点，权值 \(w_x\) 会在输入中给出，保证这类点中每个节点的权值互不相同。
• 否则，它的权值有 \(p_x\) 的概率是它子节点权值的最大值，\(1-p_x\) 的概率是最小值。

假设根节点 \(1\) 的权值有 \(m\) 种可能，第 \(i\) 小的权值是 \(v_i\)，概率是 \(d_i\,(d_i>0)\)，求 \(\sum_{i=1}^m i\cdot v_i\cdot d_i^2\bmod 998244353\)。

\(1\leq n\leq 3\times 10^5\)，\(1\leq w_i\leq 10^9\)，\(0<p_i\cdot 10000<10000\)，易证明所有叶子的权值都有概率被根取到。

朴素 DP：设 \(f_{x,i}\) 表示考虑了 \(x\) 的子树，\(x\) 的权值为 \(i\) 的概率。

\[f_{x,i}=f_{lc_x,i}\times (p \sum_{j=1}^{i-1}f_{rc_x,j}+(1-p) \sum_{j=i+1}^m f_{rc_x,j})+f_{rc_x,i}\times (p \sum_{j=1}^{i-1}f_{lc_x,j}+(1-p)\sum_{j=i+1}^m f_{lc_x,j}) \]

注意到，这个式子关系到前后缀和，并且对于 \(x\)，只有 \(x\) 的子树中存在权值为 \(i\) 的点，\(f_{x,i}\) 才有值。

考虑对每个 \(x\) 建立一棵动态开点线段树，下标为 \(i\) 的位置的值为 \(f_{x,i}\)，每个节点维护区间 \(f\) 的和 \(sum\)。

合并 \(f_x,f_y\) 到 \(f_{fa}\) 时，在 dfs 时维护 \(x_l,x_r,y_l,y_r\) 表示 \(\displaystyle \sum_{i=1}^{l-1} f_{x,i},\sum_{i=r+1}^m f_{x,i},\sum_{i=1}^{l-1}f_{y,i},\sum_{i=r+1}^m f_{y,i}\)，其中 \([l,r]\) 为当前递归的区间。如果递归到某个位置 \(y\) 对应节点为空，则 \(f_{y,l},f_{y,l+1},\cdots,f_{y,r}\) 均为 \(0\)，\(f_{fa,i}=f_{x,i}\times (p\times y_l+(1-p)\times y_r)\)（因为 \(\sum_{j=l}^r f_{y,j}=0\)，\(\sum_{j=1}^{i-1}f_{y,j}=\sum_{j=1}^{l-1}f_{y,j}\)），令 \(sum_x\gets sum_x\times (p\times y_l+(1-p)\times y_r)\)，并整体打一个 \(\times (p\times y_l+(1-p)\times y_r)\) 的 tag 即可。其他都和普通的线段树合并一样。

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5,mod=998244353;
int n,x,a[N],t,b[N],tot,rt[N],lc[N<<6],rc[N<<6],s[N<<6],tag[N<<6],p,ans;
vector<int>v[N];
void upd(int p,int v){s[p]=1ll*s[p]*v%mod,tag[p]=1ll*tag[p]*v%mod;}
void pushdown(int p){upd(lc[p],tag[p]),upd(rc[p],tag[p]),tag[p]=1;}
void modify(int &p,int l,int r,int pos){
	if(!p) p=++tot,tag[p]=1; s[p]++;
	if(l==r) return ;
	int mid=(l+r)/2;
	if(pos<=mid) modify(lc[p],l,mid,pos);
	else modify(rc[p],mid+1,r,pos);
}
void merge(int &x,int y,int l,int r,int xl,int xr,int yl,int yr){
	if(!x||!y){
		if(y) swap(xl,yl),swap(xr,yr),x=y;
		return upd(x,(1ll*p*yl%mod+1ll*(1-p+mod)%mod*yr%mod)%mod);
	}
	pushdown(x),pushdown(y);
	int mid=(l+r)/2,x0=s[lc[x]],x1=s[rc[x]],y0=s[lc[y]],y1=s[rc[y]];
	merge(lc[x],lc[y],l,mid,xl,(xr+x1)%mod,yl,(yr+y1)%mod);
	merge(rc[x],rc[y],mid+1,r,(xl+x0)%mod,xr,(yl+y0)%mod,yr);
	s[x]=(s[lc[x]]+s[rc[x]])%mod;
}
void dfs(int x){
	if(!v[x].size()) modify(rt[x],1,t,lower_bound(b+1,b+1+t,a[x])-b);
	for(int y:v[x]){ 
		dfs(y);
		if(!rt[x]) rt[x]=rt[y];
		else p=a[x],merge(rt[x],rt[y],1,t,0,0,0,0);
	}
}
void dfs2(int p,int l,int r){
	if(!p) return ;
	if(l==r) return ans=(ans+1ll*l*b[l]%mod*s[p]%mod*s[p]%mod)%mod,void();
	int mid=(l+r)/2;
	pushdown(p);
	dfs2(lc[p],l,mid),dfs2(rc[p],mid+1,r);
}
signed main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&x);
		if(x) v[x].push_back(i);
	}
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		if(v[i].size()) a[i]=796898467ll*a[i]%mod;
		else b[++t]=a[i];
	} 
	sort(b+1,b+1+t),t=unique(b+1,b+1+t)-b-1;
	dfs(1),dfs2(rt[1],1,t),printf("%d\n",ans);
	return 0;
}

P6773 [NOI2020] 命运

线段树合并优化 DP

给出一棵 \(n\) 个节点的树，你可以给每条边赋上 \(0\) 或 \(1\) 的权值。有 \(m\) 条限制 \((x,y)\)（保证 \(y\) 为 \(x\) 的祖先），你需要保证 \(x\to y\) 上至少有一条边的权值为 \(1\)。求赋值方案数 \(\bmod 998244353\)。

\(1\leq n,m\leq 5\times 10^5\)。

一个显然的性质：对于限制 \((y_1,x),(y_2,x)\)，若 \(dep_{y_1}<dep_{y_2}\)，那么第二个限制满足 → 第一个限制满足。于是我们只要关心同一个下端点中，上端点最深的那个。

设 \(f_{x,i}\) 表示已经赋好了 \(x\) 子树内边的取值，在下端点在 \(x\) 子树内、还未满足的的限制中，上端点最深为 \(i\) 的方案数。将两棵子树 \(x,y\) 合并，其中 \(x\) 是 \(y\) 的父亲：

• 若 \((x,y)\) 的权值为 \(1\)，那么显然 \(y\) 子树内所有未满足的限制，此时都满足了，\(i\) 只能由 \(x\) 贡献，\(f_{x,i}\gets f_{x,i}\sum_{j=1}^{dep_x}f_{y,j}\)。
• 否则 \(f_{x,i}\gets \sum_{\max(j,k)=i}f_{x,j}f_{y,k}=f_{x,i}\sum_{j=1}^i f_{y,j}+f_{y,i}\sum_{j=1}^{i-1}f_{x,j}\)。

\(ans=f_{1,0}\)。和上一题一样，只有 \(x\) 的子树中存在 \(mxd=i\) 的点，\(f_{x,i}\) 才有值，遇到这类前缀和形式的转移方程式，可想到用线段树合并优化。在 dfs 时维护 \(s_x,s_y\) 表示 \(\sum_{i=1}^{l-1}f_{x,i},\sum_{i=1}^{dep_x}f_{y,i}+\sum_{i=1}^{l-1} f_{y,i}\)。当某个节点 \(y\) 为空时，\(f_{y,l},f_{y,l+1},\cdots,f_{y,r}=0\)，\(f_{x,i}\gets f_{x,i}\times s_y\)。当 \(l=r\) 时，记得加 \(s_y\) 里没算的 \(f_{y,l}\) 的贡献。具体见代码。

时间复杂度 \(\mathcal O(n\log n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,mod=998244353;
int n,m,x,y,dep[N],mx,mxd[N],tot,s[N<<6],tag[N<<6],rt[N],lc[N<<5],rc[N<<5];
vector<int>v[N];
void upd(int p,int v){s[p]=1ll*s[p]*v%mod,tag[p]=1ll*tag[p]*v%mod;}
void pushdown(int p){upd(lc[p],tag[p]),upd(rc[p],tag[p]),tag[p]=1;}
void modify(int &p,int l,int r,int pos){
	if(!p) p=++tot,tag[p]=1; s[p]++;
	if(l==r) return ;
	int mid=(l+r)/2;
	if(pos<=mid) modify(lc[p],l,mid,pos);
	else modify(rc[p],mid+1,r,pos);
}
void merge(int &x,int y,int l,int r,int sx,int sy){
	if(!x||!y){
		if(y) swap(sx,sy),x=y;
		return upd(x,sy);
	}
	if(l==r) return s[x]=(1ll*s[x]*(sy+s[y])%mod+1ll*s[y]*sx%mod)%mod,void();
	pushdown(x),pushdown(y);
	int mid=(l+r)/2,x0=s[lc[x]],y0=s[lc[y]];
	merge(lc[x],lc[y],l,mid,sx,sy);
	merge(rc[x],rc[y],mid+1,r,(sx+x0)%mod,(sy+y0)%mod);
	s[x]=(s[lc[x]]+s[rc[x]])%mod;
}
int query(int p,int l,int r,int pos){
	if(!p) return 0;
	if(l==r) return s[p];
	int mid=(l+r)/2; pushdown(p);
	if(pos<=mid) return query(lc[p],l,mid,pos);
	return (s[lc[p]]+query(rc[p],mid+1,r,pos))%mod;
}
void dfs(int x,int fa){
	mx=max(mx,dep[x]=dep[fa]+1);
	for(int y:v[x]) if(y!=fa) dfs(y,x);
}
void dfs2(int x,int fa){
	modify(rt[x],0,mx,mxd[x]);
	for(int y:v[x])
		if(y!=fa) dfs2(y,x),merge(rt[x],rt[y],0,mx,0,query(rt[y],0,mx,dep[x]));
}
signed main(){
	scanf("%d",&n);
	for(int i=1;i<n;i++)
		scanf("%d%d",&x,&y),v[x].push_back(y),v[y].push_back(x);
	dfs(1,0),scanf("%d",&m);
	for(int i=1;i<=m;i++)
		scanf("%d%d",&x,&y),mxd[y]=max(mxd[y],dep[x]);
	dfs2(1,0),printf("%d\n",query(rt[1],0,mx,0));
	return 0; 
}

P7219 [JOISC2020] 星座 3，也用到了这个 trick。

二、线段树分裂

对于一个区间 \([l,r]\)，假设原状态为 \(x\)，分裂出来的状态为 \(y\)，需要保留原树的前 \(k\) 个数。

• 若 \(k<sz_{lc_x}\)，说明 \(rc_x\) 要给 \(y\)，并且左儿子继续分裂。
• 若 \(k=sz_{lc_x}\)，说明 \(rc_x\) 要给 \(y\)。
• 若 \(k>sz_{lc_x}\)，说明 \(rc_x\) 要继续分裂，\(k\gets k-sz_{lc_x}\)。

边界：\(x=0\)，此时节点为空。显然，一次分裂只需 \(\log n\) 的时间。

P5494 【模板】线段树分裂

对于 \(0\) 操作，将 \([1,n]\) 分裂成 \([1,x-1],[x,y],[y+1,n]\)，再将 \([1,x-1]\) 与 \([y+1,n]\) 合并即可。

对于 \(1\) 操作，将 \(p,t\) 两棵线段树进行线段树合并。

剩下的操作，权值线段树随便做。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+5;
int n,m,a[N],op,p,x,y,cnt=1,tot,rt[N],lc[N<<5],rc[N<<5],tmp;
ll sz[N<<5];
void build(int &p,int l,int r){
	p=++tot;
	if(l==r){sz[p]=a[l];return ;}
	int mid=(l+r)/2;
	build(lc[p],l,mid);
	build(rc[p],mid+1,r); 
	sz[p]=sz[lc[p]]+sz[rc[p]];
} 
void modify(int &p,int l,int r,int pos,int v){
	if(!p) p=++tot;
	sz[p]+=v;
	if(l==r) return ;
	int mid=(l+r)/2;
	if(pos<=mid) modify(lc[p],l,mid,pos,v);
	else modify(rc[p],mid+1,r,pos,v);
}
void merge(int &x,int y){
	if(!x||!y){x|=y;return ;}
	merge(lc[x],lc[y]),merge(rc[x],rc[y]),sz[x]+=sz[y];
}
void split(int x,int &y,ll k){
	if(!x) return ;
	y=++tot;
	if(k>sz[lc[x]]) split(rc[x],rc[y],k-sz[lc[x]]);
	else swap(rc[x],rc[y]);
	if(k<sz[lc[x]]) split(lc[x],lc[y],k);
	sz[y]=sz[x]-k,sz[x]=k;
}
int kth(int p,int l,int r,ll k){
	if(l==r) return k<=sz[p]?l:-1;
	int mid=(l+r)/2;
	if(k<=sz[lc[p]]) return kth(lc[p],l,mid,k);
	return kth(rc[p],mid+1,r,k-sz[lc[p]]);
}
ll rk(int p,int l,int r,int v){
	if(l==r) return 0;
	int mid=(l+r)/2;
	if(v<=mid) return rk(lc[p],l,mid,v);
	return sz[lc[p]]+rk(rc[p],mid+1,r,v); 
}
signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(rt[1],1,n);
	while(m--){
		scanf("%d%d%d",&op,&p,&x);
		if(!op){
			scanf("%d",&y);
			ll k1=rk(rt[p],1,n,x),k2=rk(rt[p],1,n,y+1);
			split(rt[p],rt[++cnt],k1),split(rt[cnt],tmp,k2-k1),merge(rt[p],tmp);
		}
		if(op==1) merge(rt[p],rt[x]);
		if(op==2) scanf("%d",&y),modify(rt[p],1,n,y,x);
		if(op==3) scanf("%d",&y),printf("%lld\n",rk(rt[p],1,n,y+1)-rk(rt[p],1,n,x));
		if(op==4) printf("%d\n",kth(rt[p],1,n,x));
	}
	return 0;
}

三、线段树分治

离线，按时间分治，维护支持插入、不支持删除的数据结构（支持撤销，用栈记录更新操作再回退）。若一次询问或修改仅对一段时间有效，一段时间的修改可以拆分成若干小时间段的修改，就可以线段树分治。

按时间轴建一棵线段树。对于一个加入操作，如果它的持续时间为 \([l,r]\)，就在线段树上找到 \([l,r]\) 对应的 log 个区间并加入该操作（存在节点的 vector 里）。最后，遍历整棵线段树，向儿子走表示加入子节点的操作贡献，向父亲走表示撤销当前节点的所有操作。时刻 \(t\) 时的数据结构，就是从根节点遍历到 \([t,t]\) 时的数据结构。

注意，递归到叶子时不能回答完询问后直接返回，不要忘记撤销修改。否则叶子处的修改会一直保留。

void modify(int p,int l,int r,int lx,int rx,/*操作*/ v){	//操作 v 在 [lx,rx] 时刻有效
	if(l>=lx&&r<=rx){a[p].push_back(v);return ;}	//a[p] 表示节点 p 对应的时间区间 [l,r] 上存活的元素，将 v 插入其中
	int mid=(l+r)/2;
	if(lx<=mid) modify(p<<1,l,mid,lx,rx,v);
	if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,v); 
}
void dfs(int p,int l,int r){
	for(int i:a[p]) /*计算 i 的贡献，或执行操作*/;	//[l,r] 时刻的影响
    int mid=(l+r)/2;
	if(l==r) /*输出答案*/;	//若此时刻有询问操作，则回答询问
	else dfs(p<<1,l,mid),dfs(p<<1|1,mid+1,r);	//递归左右儿子
	/*撤销贡献或操作*/; 
} 

P5631 最小 mex 生成树

给定 \(n\) 个点 \(m\) 条边的无向连通图，边有边权。

设一个自然数集合 \(S\) 的 \(\text{mex}\) 为：最小的、没有出现在 \(S\) 中的自然数。

现在你要求出一个这个图的生成树，使得其边权集合的 \(\text{mex}\) 尽可能小。

\(1\leq n\leq 10^6\)，\(1\leq m\leq 2\times 10^6\)，\(0\leq w\leq 10^5\)。

由于 \(\text{mex}\) 没有出现的最小自然数，所以若去掉边权为 \(x\) 的边后图不连通，则所有生成树一定都包含边权为 \(x\) 的边，\(x\) 就不可能成为某个生成树的 \(\text{mex}\)。

故只需对于每个 \(x\)，看去掉边权为 \(x\) 的边后图是否连通。注意到删边不太好维护，考虑线段树分治 + 并查集。具体来说，建一棵以边权为下标的线段树，对于每条边权为 \(w\) 的边将其放到 \([0,w-1]\) 和 \([w+1,10^5]\) 上，这样到叶节点时就连上了所有不包含该边权的边，判断图是否连通即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,m,t=1e5,u[N<<1],v[N<<1],w[N<<1],f[N],sz[N],top;
vector<int>a[N<<2];
pair<int,int>s[N];
int find(int x){return x==f[x]?x:find(f[x]);}
void merge(int x,int y){
	x=find(x),y=find(y);
	if(x!=y){ 
		if(sz[x]<sz[y]) swap(x,y);
		s[++top]={x,y},f[y]=x,sz[x]+=sz[y];
	} 
}
void undo(int p){
	while(p<top){
		int x=s[top].first,y=s[top--].second;
		f[y]=y,sz[x]-=sz[y];
	}
}
void modify(int p,int l,int r,int lx,int rx,int id){
	if(lx>rx) return ;
	if(l>=lx&&r<=rx){a[p].push_back(id);return ;}
	int mid=(l+r)/2;
	if(lx<=mid) modify(p<<1,l,mid,lx,rx,id);
	if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,id); 
}
void dfs(int p,int l,int r){
	int x=top; 
	for(int i:a[p]) merge(u[i],v[i]);
	int mid=(l+r)/2;
	if(l==r){if(sz[find(1)]==n) printf("%d\n",l),exit(0);} 
	else dfs(p<<1,l,mid),dfs(p<<1|1,mid+1,r);
	undo(x);
}
signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) f[i]=i,sz[i]=1;
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&u[i],&v[i],&w[i]);
		modify(1,0,t,0,w[i]-1,i),modify(1,0,t,w[i]+1,t,i);
	}
	dfs(1,0,t);
	return 0; 
}

四、历史值问题

要考虑标记时间的先后顺序。

对于询问一个区间的所有子区间，扫描线 \(r\)，不同的 \(r\) 看作不同历史版本，转化为历史值问题。

对于询问一个矩阵，扫描线 \(x\)，不同的 \(x\) 看作不同历史版本，也可以转化为历史值问题。

两者本质相同，就是把子区间 \([l,r]\) 看作平面上一个点 \((l,r)\)，一个区间的所有子区间就是平面上一个矩阵。

A1

区间加，查询区间最大值，查询区间历史最大值的最大值。

当前的 info \((mx,hmx)\) 经过 \(+v_1,+v_2,\cdots,+v_k\) 后，设 \(s_i\) 为 \(v_i\) 的前缀和，则会变成 \((mx+s_k,\max(hmx,mx+\max s_i))\)。所以 tag 需要维护当前的 \(s_k\) 和 \(s_i\) 的历史最大值 \(mxs\)。

将 \(fa\) 的 tag 下传到 \(x\) 时，不难发现 \(s_x'\gets s_x+s_{fa}\)，\(mxs_x'\gets \max(mxs_x,s_x+mxs_{fa})\)，下传完重置 \(s_{fa}=mxs_{fa}=0\)。

打新标记时，先将所有祖先的标记下传到它身上，清空祖先标记，再打上新标记，体现了时间的先后性。

struct tag{
	int s,mxs;
	void upd(tag tg){mxs=max(mxs,s+tg.mxs),s+=tg.s;}
}tg[N<<2];
struct info{
	int mx,hmx;
	void upd(tag tg){hmx=max(hmx,mx+tg.mxs),mx+=tg.s;}
	info operator+(info a){return {max(mx,a.mx),max(hmx,a.hmx)};}
}s[N<<2];
void upd(int p,tag v){
	s[p].upd(v),tg[p].upd(v);
}
void down(int p){
	upd(p<<1,tg[p]),upd(p<<1|1,tg[p]),tg[p].s=tg[p].mxs=0;
}

简洁版：

int s[N<<2],mxs[N<<2],mx[N<<2],hmx[N<<2];
void push(int p){
	mx[p]=max(mx[p<<1],mx[p<<1|1]);
	hmx[p]=max(hmx[p<<1],hmx[p<<1|1]);
}
void upd(int p,int t1,int t2){
	hmx[p]=max(hmx[p],mx[p]+t2),mx[p]+=t1;
	mxs[p]=max(mxs[p],s[p]+t2),s[p]+=t1;
}
void down(int p){
	upd(p<<1,s[p],mxs[p]),upd(p<<1|1,s[p],mxs[p]),s[p]=mxs[p]=0;
}

A2

P4314 CPU 监控

区间加，区间赋值，查询区间最大值，查询区间历史最大值的最大值。

容易发现，如果存在赋值标记，那么区间的所有数都会变得相同，之后的加法操作也可以视为赋值。于是标记们可以转化为一堆加法标记紧跟着一堆赋值标记，或者只有一堆加法标记没有赋值标记。

（技巧：将赋值之后的加法也看成是赋值，使 加法 赋值 “分层”）

当前的 info \((mx,hmx)\) 经过赋值 \(c_1,c_2,\cdots,c_k\) 后，则会变成 \((c_k,\max(hmx,\max c_i))\)。所以 tag 还需要维护：\(fc\) 表示是否有赋值操作，\(c\) 表示当前的 \(c_k\)，\(mxc\) 表示 \(\max c_i\)。

打加法标记时，若 \(fc_x=1\) 则要将加法标记改为赋值标记。

当 \(fc_{fa}=1\) 则需要下传赋值标记，\(fc_x'\gets 1\)，\(c_x'\gets c_{fa}\)，\(mxc_x'\gets\begin{cases}\max(mxc_x,mxc_{fa})&(fc_x=1)\\mxc_{fa}&(fc_x=0)\end{cases}\)，然后重置 \(fc_{fa}=0\)。

struct tag{
	int s,mxs,fc,c,mxc;
	void upd(tag tg){
		if(fc) mxc=max(mxc,c+tg.mxs),c+=tg.s;	//加法操作（如果之前有赋值操作了要改成赋值）
		else mxs=max(mxs,s+tg.mxs),s+=tg.s;
		if(tg.fc) c=tg.c,mxc=fc?max(mxc,tg.mxc):tg.mxc,fc=1;	//赋值操作
	}
}tg[N<<2];
struct info{
	int mx,hmx;
	void upd(tag tg){
		hmx=max(hmx,mx+tg.mxs),mx+=tg.s;
		if(tg.fc) mx=tg.c,hmx=max(hmx,tg.mxc);
	}
	info operator+(info a){return {max(mx,a.mx),max(hmx,a.hmx)};}
}s[N<<2];
void upd(int p,tag v){
	s[p].upd(v),tg[p].upd(v);
}
void down(int p){
	upd(p<<1,tg[p]),upd(p<<1|1,tg[p]),tg[p].s=tg[p].mxs=tg[p].fc=0;
}

A3

SP1557 GSS2 - Can you answer these queries II

多次询问一个区间的最大子段和，相同的数只算一次。

即询问一个区间中所有子区间相同数只算一次时的和的最大值。

离线，扫描线 \(r\)，不同的 \(r\) 看作不同历史版本，扫的过程中线段树上第 \(l\) 个位置维护 \([l,r]\) 相同数只算一次的和。处理相同数就是加入 \(a_r\) 时只对线段树上的 \([pre_{a_r}+1,r]\) 区间 \(+a_r\)。这样就转化为了区间加，询问区间历史最大值的最大值。

signed main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	scanf("%d",&m);
	for(int i=1;i<=m;i++)
		scanf("%d%d",&l,&r),v[r].push_back({l,i}); 
	for(int i=1;i<=n;i++){
		modify(1,1,n,lst[a[i]+o]+1,i,a[i]),lst[a[i]+o]=i;
		for(auto p:v[i]) ans[p.second]=query(1,1,n,p.first,i);
	}
	for(int i=1;i<=m;i++) printf("%lld\n",ans[i]);
	return 0;
}

A4

P6109 [Ynoi2009] rprmq1

总结：二维问题可将一维看作时间轴，转化为历史版本问题。将前缀移植到区间上，可以考虑分治。

有一个 \(n\times n\) 的矩阵 \(a\)，初始全为 \(0\)。先进行 \(m\) 次子矩阵加，再进行 \(q\) 次查询子矩阵最大值。

\(1\leq n,m\leq 5\times 10^4\)，\(1\leq q\leq 5\times 10^5\)，\(1\leq v\leq 2147483647\)，4s。

考虑一条竖线从左到右扫，修改就是扫到 \(x=l_1\) 时对 \(y\in[l_2,r_2]\) 区间 \(+v\)，扫到 \(x=r_1+1\) 时对 \(y\in[l_2,r_2]\) 区间 \(-v\)，询问就是问区间 \([l_2,r_2]\) 在从 \(x=l_1\) 扫到 \(x=r_1\) 这段时间的区间历史最大值。

时间是区间的历史最大值并不好做，但时间是前缀的历史最大值好做（线段树）。

一个技巧是分治。对时间（即 \(x\) 坐标）进行猫树分治，递归到 \([l,r]\) 时，我们手里有 \([l_1,r_1]\subseteq [l,r]\) 的询问和 \([l_1,r_1]\cap[l,r]\neq\varnothing\) 的修改，现在需要处理这些修改并回答其中跨过 \(mid\) 的询问。询问的 \(x\in[l_1,r_1]\) 拆成 \(x\in[l_1,mid]\) 和 \(x\in[mid+1,r_1]\)，这样的一段后缀和一段前缀就好做了。具体地：

1. 清空历史最大值。然后一条竖线从 \(mid\) 扫到 \(l\)，对于一个 \([l_1,r_1]\cap[l,mid]\neq\varnothing\) 修改，扫到 \(x=\min(r_1,mid)\) 时对 \(y\in[l_2,r_2]\) 区间 \(+v\)。扫到一个询问的 \(l_1\) 时，\(x\in[l_1,mid]\) 已经处理好了，那么其 \(x\in[l_1,mid]\) 的历史最大值直接在线段树上查从开始扫到现在区间 \([l_2,r_2]\) 的历史最大值即可。
2. 清空历史最大值。然后一条竖线从 \(mid+1\) 扫到 \(r\)，类似。

清空历史最大值有两种方法：1. 每次修改进行备份，打标记还原。2. 比较妙的方法是，全局 \(+\infty\)，这样由于之前的值 \(<\infty\) 肯定不会是历史最大值，之后查询将结果 \(-\infty\) 即可。

但还有一个问题，容易发现一个修改会在所有与它有交的分治区间处理一次，复杂度爆炸。解决方法是，若 \([l_1,r_1]\) 完全覆盖分治区间就不需要下传了，提前操作好递归完再撤销，这样类似线段树一个修改会劈成 \(\log\) 个区间，只会处理 \(\log\) 次。

时间复杂度 \(\mathcal O((n+q)\log n+m\log^2 n)\)。

#include<bits/stdc++.h>
#define ll long long
#define pb push_back
using namespace std;
const int N=5e4+5,M=5e5+5;
int n,m,Q,xl,xr,yl,yr,v,tim;
ll inf=7e12,s[N<<2],mxs[N<<2],mx[N<<2],hmx[N<<2],ans[M];	//注意 inf 设太大就爆了，会 wa
struct P{
	int xl,xr,yl,yr,v;
};
vector<P>u,q,ins[N],del[N],qry[N];
void upd(int p,ll t1,ll t2){
	hmx[p]=max(hmx[p],mx[p]+t2),mx[p]+=t1;
	mxs[p]=max(mxs[p],s[p]+t2),s[p]+=t1;
}
void down(int p){
	upd(p<<1,s[p],mxs[p]),upd(p<<1|1,s[p],mxs[p]),s[p]=mxs[p]=0;
}
void modify(int p,int l,int r,int lx,int rx,ll v){
	if(l>=lx&&r<=rx) return upd(p,v,max(v,0ll));
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) modify(p<<1,l,mid,lx,rx,v);
	if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,v);
	mx[p]=max(mx[p<<1],mx[p<<1|1]);
	hmx[p]=max(hmx[p<<1],hmx[p<<1|1]);
}
ll query(int p,int l,int r,int lx,int rx){
	if(l>=lx&&r<=rx) return hmx[p];
	int mid=(l+r)/2; ll ans=-8e18;
	down(p);
	if(lx<=mid) ans=query(p<<1,l,mid,lx,rx);
	if(rx>mid) ans=max(ans,query(p<<1|1,mid+1,r,lx,rx));
	return ans;
}
void clear(){
	modify(1,1,n,1,n,inf),tim++;
}
void dou(vector<P>u,int v){
	for(auto i:u) modify(1,1,n,i.yl,i.yr,i.v*v);
} 
void doq(vector<P>q){
	for(auto i:q) ans[i.v]=max(ans[i.v],query(1,1,n,i.yl,i.yr)-tim*inf);
}
void solve(int l,int r,vector<P>u,vector<P>q){
	if(!q.size()) return ;	//卡常
	if(l==r) return dou(u,1),doq(q),dou(u,-1),clear();
	int mid=(l+r)/2;
	vector<P>ul,ur,al,ar,ql,qr;	//al 是完全覆盖左区间的修改，ul 是其他与左区间有交的修改
	for(int i=l-1;i<=r+1;i++)
		ins[i].clear(),del[i].clear(),qry[i].clear();
	for(auto i:u){
		if(i.xl<=mid){
			int tmp=i.xr;
			i.xr=min(i.xr,mid);
			ins[i.xr].pb(i),del[i.xl-1].pb(i),(i.xl==l&&i.xr==mid?al:ul).pb(i);
			i.xr=tmp;
		}
		if(i.xr>mid){
			i.xl=max(i.xl,mid+1);
			ins[i.xl].pb(i),del[i.xr+1].pb(i),(i.xl==mid+1&&i.xr==r?ar:ur).pb(i);
		}
	}
	for(auto i:q){
		if(i.xr<=mid) ql.pb(i);
		else if(i.xl>mid) qr.pb(i);
		else qry[i.xl].pb(i),qry[i.xr].pb(i);
	}
	for(int i=mid;i>=l-1;i--)	//注意循环到 l-1
		dou(del[i],-1),dou(ins[i],1),doq(qry[i]); clear();	//注意要先 del 再 ins，因为同时 ins +x,del -y，可能的历史最值应为 -y+x 而非 x
	for(int i=mid+1;i<=r+1;i++)
		dou(del[i],-1),dou(ins[i],1),doq(qry[i]); clear();
	dou(al,1),solve(l,mid,ul,ql),dou(al,-1),clear();
	dou(ar,1),solve(mid+1,r,ur,qr),dou(ar,-1),clear();
}
signed main(){
	scanf("%d%d%d",&n,&m,&Q);
	for(int i=1;i<=m;i++)
		scanf("%d%d%d%d%d",&xl,&yl,&xr,&yr,&v),u.pb({xl,xr,yl,yr,v});
	for(int i=1;i<=Q;i++)
		scanf("%d%d%d%d",&xl,&yl,&xr,&yr),q.pb({xl,xr,yl,yr,i});
	solve(1,n,u,q);
	for(int i=1;i<=Q;i++) printf("%lld\n",ans[i]);
	return 0;
}

B1

区间加，区间和，区间历史版本和（每次区间加后都是一个版本）。

当前 info \((sum,hsum)\) 经过 \(+v_1,+v_2,\cdots,+v_k\) 后，设 \(s_i\) 为 \(v_i\) 的前缀和，则会变成 \((sum+s_k\times len,hsum+\sum_{i=1}^k(sum+s_i\times len))=(sum+s_k\times len,hsum+sum\times k+\sum_{i=1}^k s_i\times len)\)，其中 \(len\) 表示区间长度。所以 tag 需要维护当前的 \(s_k\)、更新标记的个数 \(k\)、加法标记前缀和的历史版本和 \(ss=\sum_{i=1}^k s_i\)。

将 \(fa\) 的 tag 下传到 \(x\) 时，不难发现 \(s_x'\gets s_x+s_{fa}\)，\(k'_x\gets k_x+k_{fa}\)，\(ss_x'\gets ss_x+(s_x\times k_{fa}+ss_{fa})\)。

struct tag{
	ll s,k,ss;
	void upd(tag tg){
		if(tg.k) ss+=s*tg.k+tg.ss,k+=tg.k;
		s+=tg.s;
	}
}tg[M<<2];
struct info{
	ll sum,hsum;
	void upd(tag tg,int len){
		if(tg.k) hsum+=tg.k*sum+tg.ss*len;
		sum+=tg.s*len;
	}
	info operator+(info a){return {sum+a.sum,hsum+a.hsum};}
}s[M<<2];
void upd(int p,int l,int r,tag v){
	s[p].upd(v,r-l+1),tg[p].upd(v);
}
void down(int p,int l,int r,int mid){
	upd(p<<1,l,mid,tg[p]),upd(p<<1|1,mid+1,r,tg[p]),tg[p]={0,0,0};
}

B2

CF997E 中：区间加，询问区间历史全局最小值个数和。

info \((mn,cnt,hcnt)\)（分别表示最小值，最小值个数，历史全局最小值个数和），tag \((tg,tgc)\) 表示当前 info 会变成 \((mn+tg,cnt,hcnt+cnt\times tgc)\)。

只有左右儿子的最小值是整个区间的最小值时，才把 \(tgc\) pushdown 给它。

void push(int p){
	mn[p]=min(mn[p<<1],mn[p<<1|1]);
	cnt[p]=cnt[p<<1]*(mn[p<<1]==mn[p])+cnt[p<<1|1]*(mn[p<<1|1]==mn[p]);
}
void tag(int p,int v){tg[p]+=v,mn[p]+=v;}
void tagc(int p,int v){tgc[p]+=v,hcnt[p]+=v*cnt[p];} 
void down(int p){
	tag(p<<1,tg[p]),tag(p<<1|1,tg[p]),tg[p]=0;
	if(mn[p<<1]==mn[p]) tagc(p<<1,tgc[p]);
	if(mn[p<<1|1]==mn[p]) tagc(p<<1|1,tgc[p]);
	tgc[p]=0;
}

扩展：询问区间历史全局最小值个数带权和。比如某时刻全局最小值个数 \(\times k\) 贡献给答案。

把 tagc(p,1) 改成 tagc(p,k) 即可。

B3

P8868 [NOIP2022] 比赛 中：给出 \(a_{1\sim n},b_{1\sim n}\)，同时对 \(a,b\) 区间加，询问 \(\sum_{i=1}^n a_ib_i\) 的历史和。

由于 \(\sum(a_i+va)(b_i+vb)=\sum a_ib_i+\sum a_i\times vb+\sum b_i\times va+\sum va\times vb\)，info 除了维护 \(sab,hsab\)，还需维护 \(sa,sb\)。

当前 info \((sa,sb,sab,hsab)\) 经过 \(+va_{1\sim k},+vb_{1\sim k}\) 后，设 \(da_i,db_i\) 分别为 \(va_i,vb_i\) 的前缀和，则会变成 \(sa'\gets sa+da_k\times len\)，\(sb'\gets sb+db_k\times len\)，\(sab'\gets sab+sa\cdot db_k+sb\cdot da_k+da_k\cdot db_k\cdot len\)，\(hsab'\gets hsab+sab\times k+sa\times \sum_{i=1}^k db_i+sb\times \sum_{i=1}^k da_i+\sum_{i=1}^k da_i\times db_i\)，所以 tag 需要维护 \(k\)、\(da_k\)、\(db_k\)、\(hda=\sum_{i=1}^k da_i\)、\(hdb=\sum_{i=1}^k db_i\)、\(hdab=\sum_{i=1}^k da_i\times db_i\)。

下传：\(k_x',da_x',db_x'\) 显然，\(hda_x'\gets hda_x+da_x\times k_{fa}+hda_{fa}\)，\(hdb_x'\) 同理，展开 \(\sum_{i=1}^{k_{fa}}(da_x+{da_{fa}}_i)(db_x+{db_{fa}}_i)\) 可得 \(hdab_x'\gets hdab_x+da_x\times db_x\times k_{fa}+da_x\times hdb_{fa}+db_x\times hda_{fa}\)。

struct tag{
	ull da,db,c,ha,hb,hab;
	void upd(tag tg){
		if(c==-1) *this=tg;
		else{
			hab+=tg.hab+da*tg.hb+db*tg.ha+da*db*tg.c;
			ha+=tg.ha+da*tg.c,hb+=tg.hb+db*tg.c;
			da+=tg.da,db+=tg.db,c+=tg.c;
		}
	}
}tg[N<<2];
struct info{
	ull sa,sb,sab,hab;
	void upd(tag tg,int len){
		hab+=sab*tg.c+sa*tg.hb+sb*tg.ha+tg.hab*len;
		sab+=sa*tg.db+sb*tg.da+tg.da*tg.db*len;
		sa+=tg.da*len,sb+=tg.db*len;
	}
	info operator+(info x){
		return {sa+x.sa,sb+x.sb,sab+x.sab,hab+x.hab};
	}
}s[N<<2];
void upd(int p,int l,int r,tag v){
	s[p].upd(v,r-l+1),tg[p].upd(v);
}
void down(int p,int l,int r,int mid){
	if(~tg[p].c) upd(p<<1,l,mid,tg[p]),upd(p<<1|1,mid+1,r,tg[p]),tg[p].c=-1;
}

B4

Gym103069G Prof. Pang's sequence

询问一个区间中有多少子区间颜色数为奇数。

类似 A3，离线，扫描线 \(r\)，加入 \(a_r\) 时 \(l\in[pre_{a_r}+1,r]\) 的区间颜色数奇偶性 \(\oplus 1\)。转化为 01 序列区间取反，查询历史区间和。

由于一个区间只有取反和不取反两种状态，所以可以分别维护。类似 B2。

void tag(int p){
	tg[p]^=1,swap(c0[p],c1[p]),swap(s0[p],s1[p]),swap(tc0[p],tc1[p]);
}
void tagc0(int p,int v){tc0[p]+=v,s0[p]+=1ll*c0[p]*v;}
void tagc1(int p,int v){tc1[p]+=v,s1[p]+=1ll*c1[p]*v;}
void down(int p){
	if(tg[p]) tag(p<<1),tag(p<<1|1),tg[p]=0;
	if(tc0[p]) tagc0(p<<1,tc0[p]),tagc0(p<<1|1,tc0[p]),tc0[p]=0;
	if(tc1[p]) tagc1(p<<1,tc1[p]),tagc1(p<<1|1,tc1[p]),tc1[p]=0;
}
void modify(int p,int l,int r,int lx,int rx){	//区间取反
	if(l>=lx&&r<=rx) return tag(p);
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) modify(p<<1,l,mid,lx,rx);
	if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx);
	c0[p]=c0[p<<1]+c0[p<<1|1],c1[p]=c1[p<<1]+c1[p<<1|1];
	s0[p]=s0[p<<1]+s0[p<<1|1],s1[p]=s1[p<<1]+s1[p<<1|1];
}
//每次 tagc1(1,1)

五、兔队线段树

即线段树维护单调栈，处理前缀最值相关。

P4198 楼房重建

给出 \(a_{1\sim n}\)，支持单点修改，每次求区间上升序列的长度，其中上升序列指由前缀最大值组成的序列。

\(n,q\leq 10^5\)。

维护 \(ans\)，合并两个区间时，先 \(ans_p\gets ans_{lc_p}\)，当前结尾是 \(mx_{lc_p}\)，要算 \(rc_p\) 以 \(mx_{lc_p}\) 开头的上升序列长度。

写一个 \(G(p,pre)\) 算区间 \(p\) 以 \(pre\) 开始的上升序列长度：

• 若 \(pre\geq mx_{lc_p}\)，\(G(p,pre)\gets G(rc_p,pre)\)。
• 否则 \(pre<mx_{lc_p}\)，\(G(p,pre)\gets G(lc_p,pre)+G(rc_p,mx_{lc_p})\)，\(G(rc_p,mx_{lc_p})\) 与 \(pre\) 无关。发现 \(ans_p=G(p,0)=G(lc_p,0)+G(rc_p,mx_{lc_p})\)，所以 \(G(rc_p,mx_{lc_p})=ans_p-ans_{lc_p}\)。

现在两种情况都只往一边递归，算一次 \(G\) 是 \(\mathcal O(\log n)\) 的。

upd on 2023.8.5：如果维护“整个子树的信息和”没法维护可减信息。但维护“考虑整个子树时右儿子的信息和（受左儿子限制）”就可以，只要满足结合律就可以维护。

一个类似的问题

2023.11.14

有一些区间 \([l_r,r]\subseteq[1,n]\)，多次询问 \(|\cup_{j=x}^y[l_j,j]|\)。

从右往左考虑所有 \(j\)（因为后面的区间可能被覆盖到前面，而前面的区间不可能覆盖到后面）。

考虑 \([a,b]\) 有多少位置被覆盖时，只需要考虑：1. \(j\in[a,b]\) 的 \([l_j,j]\)；2. \(j>b\) 的 \([l_j,j]\) 中 \(l_j\) 最小的。

类似楼房重建，写一个 \(G(p,v)\) 算，\(j\) 在区间 \(p\) 后面的 \(\min l_j\) 是 \(v\)，区间 \(p\) 有多少位置被覆盖。

• 若 \(v>mid\)，\(G(p,v)\gets G(rc_p,v)+G(lc_p,mn_{rc_p})\)，\(G(lc_p,mn_{rc_p})\) 与 \(v\) 无关，可以 pushup 时记录。
• 否则 \(v\leq mid\)，\(G(p,v)\gets r-mid+G(lc_p,\min(v,mn_{rc_p}))\)。

其中 \(mn_p\) 表示 \(\min_{j\in I_p}l_j\)。

两种情况都只往一边递归，算一次 \(G\) 是 \(\mathcal O(\log n)\) 的。

int calc(int p,int l,int r,int v){
	if(l==r) return v<=l||vis[l];	//vis[i] 表示是否存在以 i 为右端点的区间
	int mid=(l+r)/2;
	if(v>mid) return calc(p<<1|1,mid+1,r,v)+sum[p];
	return r-mid+calc(p<<1,l,mid,min(v,mn[p<<1|1]));
}
void push(int p,int l,int mid){
	mn[p]=min(mn[p<<1],mn[p<<1|1]);
	sum[p]=calc(p<<1,l,mid,mn[p<<1|1]);
}
void query(int p,int l,int r,int lx,int rx){
	if(l>=lx&&r<=rx){ans+=calc(p,l,r,Mn),Mn=min(Mn,mn[p]);return ;}
	int mid=(l+r)/2;
	if(rx>mid) query(p<<1|1,mid+1,r,lx,rx);
	if(lx<=mid) query(p<<1,l,mid,lx,rx);
}

Gym102012E Rikka with Data Structures

2023.3.2

给出 \(a_{1\sim n}\)，\(m\) 次操作：

• 1 l r v：\(\forall i\in[l,r]\)，\(a_i\gets a_i+v\)。
• 2 l r v：\(\forall i\in[l,r]\)，\(a_i\gets v\)。
• 3 l r x：询问有多少 \(y\in[l,r]\) 满足 \(\max(a_{\min(x,y)\sim \max(x,y)})=\max(a_x,a_y)\)。

\(1\leq T\leq 200\)，\(1\leq n,m\leq 10^5\)，\(1\leq a_i,v\leq 10^9\)，最多 \(10\) 组数据满足 \(n>10^3\) 或 \(m>10^3\)。

有 \(x<l,x>r,l\leq x\leq r\) 三种情况，第三种情况 \(x\) 本身肯定是答案，可以分成 \([l,x-1],[x+1,r]\)，这样就只剩前两种情况了。

以 \(x<l\) 为例，可以用 \(y\in[x,r]\) 的答案减去 \(y\in[x,l-1]\) 的答案。转化为求单看区间 \([x,r]\)，前缀最大值的位置数量。用楼房重建的方法做，维护节点最大值、以节点首元素为开头的单调栈长度，只不过这里不是 \([1,n]\) 而是一个区间。我们可以把 \([x,r]\) 分为 \(\mathcal O(\log n)\) 个线段树区间，然后用前一个区间的最大值作为下一个区间的单调栈开头元素传入。

时间复杂度 \(\mathcal O(Tm\log^2 n)\)。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+5;
int t,n,m,a[N],op,l,r,x,ans;
struct Seg{
	int tg[N<<2],sum[N<<2];
	ll ad[N<<2],mx[N<<2];
	void add(int p,ll v){mx[p]+=v,ad[p]+=v;}
	void cov(int p,int l,int r,int v){mx[p]=tg[p]=v,ad[p]=0,sum[p]=r-l+1;}
	void down(int p,int l,int r,int mid){
		if(tg[p]) cov(p<<1,l,mid,tg[p]),cov(p<<1|1,mid+1,r,tg[p]),tg[p]=0;
		if(ad[p]) add(p<<1,ad[p]),add(p<<1|1,ad[p]),ad[p]=0;
	}
	int calc(int p,int l,int r,ll v){
		if(l==r) return mx[p]>=v;
		int mid=(l+r)/2;
		down(p,l,r,mid);
		if(v<=mx[p<<1]) return calc(p<<1,l,mid,v)+sum[p]-sum[p<<1];
		return calc(p<<1|1,mid+1,r,v);
	}
	void push(int p,int r,int mid){
		mx[p]=max(mx[p<<1],mx[p<<1|1]);
		sum[p]=sum[p<<1]+calc(p<<1|1,mid+1,r,mx[p<<1]);	//楼房重建
	}
	void build(int p,int l,int r){
		tg[p]=ad[p]=0;
		if(l==r){mx[p]=a[l],sum[p]=0;return ;}
		int mid=(l+r)/2;
		build(p<<1,l,mid);
		build(p<<1|1,mid+1,r);
		push(p,r,mid);
	}
	void modify(int p,int l,int r,int lx,int rx,int v,int op){
		if(l>=lx&&r<=rx) return op==1?add(p,v):cov(p,l,r,v);
		int mid=(l+r)/2;
		down(p,l,r,mid);
		if(lx<=mid) modify(p<<1,l,mid,lx,rx,v,op);
		if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,v,op);
		push(p,r,mid);
	}
	ll qry(int p,int l,int r,int pos){	//查询单个位置
		if(l==r) return mx[p];
		int mid=(l+r)/2;
		down(p,l,r,mid);
		if(pos<=mid) return qry(p<<1,l,mid,pos);
		return qry(p<<1|1,mid+1,r,pos);
	}
	int find(int p,int l,int r,int pos,ll v){	//查询 pos 及其后面第一个 >v 的位置。复杂度是 1log 的，可以看成是先定位到 [pos,n] 再往下二分
		if(mx[p]<=v) return n+1;
		if(l==r) return l;
		int mid=(l+r)/2,tmp;
		down(p,l,r,mid);
		if(pos<=mid&&(tmp=find(p<<1,l,mid,pos,v))<=n) return tmp;
		return find(p<<1|1,mid+1,r,pos,v);
	}
	int query(int p,int l,int r,int lx,int rx,ll &pre){	//把 [lx,rx] 分为 log 个线段树区间，用前一个区间的最大值作为下一个区间单调栈的开头传入
		if(l>=lx&&r<=rx){
			int ans=calc(p,l,r,pre);
			return pre=max(pre,mx[p]),ans;
		}
		int mid=(l+r)/2,ans=0;
		down(p,l,r,mid);
		if(lx<=mid) ans=query(p<<1,l,mid,lx,rx,pre);
		if(rx>mid) ans+=query(p<<1|1,mid+1,r,lx,rx,pre);
		return ans;
	}
	int ask(int x,int r){
		int pos=find(1,1,n,x,qry(1,1,n,x)); ll tmp=0;
		return pos>r?r-x+1:pos-x+query(1,1,n,pos,r,tmp);
	}
}A,B;
signed main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++) scanf("%d",&a[i]);
		A.build(1,1,n),reverse(a+1,a+1+n),B.build(1,1,n);
		while(m--){
			scanf("%d%d%d%d",&op,&l,&r,&x);
			if(op<=2) A.modify(1,1,n,l,r,x,op),B.modify(1,1,n,n-r+1,n-l+1,x,op);
			else{
				ans=0;
				if(x<=r) ans+=A.ask(x,r)-(x<l?A.ask(x,l-1):0);
				if(x>=l) ans+=B.ask(n-x+1,n-l+1)-(x>r?B.ask(n-x+1,n-(r+1)+1):0);
				printf("%d\n",ans-(x>=l&&x<=r));	//x>=l&&x<=r 时 x 被算了两次
			}
		}
	}
	return 0;
}

六、Segment tree Beats

一般有两类方法：

• 复合型标记。

  比如标记 \((add,v)\) 表示先加 \(add\) 再对 \(v\) 取 \(\max\)。

• 数域划分。

  本质上是通过维护最大值/严格次大值/最小值/严格次小值，将区间取 \(\min\) / \(\max\) 操作，转化成一种只针对区间最大值/最小值进行加减修改的操作。比如，打 \(\min\) 标记时，只有区间中的最大值会受到这一标记的影响，其余数都是不变的，且最大值被修改后，原来是区间最大值的所有数仍然是区间最大值。

  把线段树上一个节点的数分成三类——最大值、最小值、既不是最大值也不是最小值，然后对每一类数分别维护它们的标记与信息。

A1

HDU5306 Gorgeous Sequence

维护一个序列，支持：

• 修改：区间对一个数 \(v\) 取 \(\min\)。
• 查询：区间求 \(\max\)，区间求和。

info：区间最大值 \(mx\)，严格次大值 \(mx2\)，最大值出现次数 \(cnt\)，区间和 \(sum\)。

tag：\(tg\) 表示区间里所有的 \(mx\) 要改为 \(tg\)。

down：若 \(lc_p,rc_p\) 的 \(mx\) 与 \(p\) 相同就下传。

区间对 \(v\) 取 \(\min\) 时：

• 若 \(mx\leq v\)：return。
• 若 \(mx2\leq v<mx\)：打标记，return。
• 若 \(v<mx2\)：暴力递归。

\(mx2\leq v<mx\)，\(mx\) 对 \(v\) 取 \(\min\) 时：\(mx'\gets v\)，\(sum'\gets sum-(mx-v)\cdot cnt\)。

复杂度分析：初始线段树上所有区间的数的种类数之和是 \(\mathcal O(n\log n)\) 的，每递归经过一个 \(v<mx2\) 的区间一定会将 \(mx,mx2\) 的数都改为 \(v\)，导致区间的数的种类数至少 \(-1\)。再加上区间操作本身的复杂度 \(\mathcal O(m\log n)\)，时间复杂度 \(\mathcal O((n+m)\log n)\)。

void upd(int p,int v){
	sum[p]-=1ll*(mx[p]-v)*cnt[p],tg[p]=mx[p]=v;	//!!! 某 sb 没写 1ll
}
void down(int p){
	if(~tg[p]){
		int mx_=max(mx[p<<1],mx[p<<1|1]);	//mx[p] 已经被改掉了，原来的 mx[p] 是 mx_
		if(mx[p<<1]==mx_) upd(p<<1,tg[p]);
		if(mx[p<<1|1]==mx_) upd(p<<1|1,tg[p]);
		tg[p]=-1;
	}
}
void modify(int p,int l,int r,int lx,int rx,int v){
	if(mx[p]<=v) return ;
	if(l>=lx&&r<=rx&&mx2[p]<=v) return upd(p,v);
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) modify(p<<1,l,mid,lx,rx,v);
	if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}

实现的小技巧：不需要记录 \(tg\)，直接将 \(mx_p\) 当做 \(tg\) 下传给儿子节点即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5,M=N<<2;
int t,n,m,a[N],op,l,r,v,mx[M],mx2[M],cnt[M],Mx;
long long sum[M],Sum;
void push(int p){
	sum[p]=sum[p<<1]+sum[p<<1|1];
	mx[p]=max(mx[p<<1],mx[p<<1|1]);
	mx2[p]=max(mx[p]^mx[p<<1]?mx[p<<1]:mx2[p<<1],mx[p]^mx[p<<1|1]?mx[p<<1|1]:mx2[p<<1|1]);
	cnt[p]=(mx[p]==mx[p<<1]?cnt[p<<1]:0)+(mx[p]==mx[p<<1|1]?cnt[p<<1|1]:0);
}
void build(int p,int l,int r){
	if(l==r){mx[p]=sum[p]=a[l],mx2[p]=-1,cnt[p]=1;return ;}
	int mid=(l+r)/2;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	push(p);
}
void upd(int p,int v){	//p 对应区间对 v 取 min，保证 mx2[p]<=v<mx[p]
	sum[p]-=1ll*(mx[p]-v)*cnt[p],mx[p]=v;
}
void down(int p){
	if(mx[p]<mx[p<<1]) upd(p<<1,mx[p]);
	if(mx[p]<mx[p<<1|1]) upd(p<<1|1,mx[p]);
}
void modify(int p,int l,int r,int lx,int rx,int v){
	if(mx[p]<=v) return ;
	if(l>=lx&&r<=rx&&mx2[p]<=v) return upd(p,v);
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) modify(p<<1,l,mid,lx,rx,v);
	if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void query(int p,int l,int r,int lx,int rx){
	if(l>=lx&&r<=rx){Mx=max(Mx,mx[p]),Sum+=sum[p];return ;}
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) query(p<<1,l,mid,lx,rx);
	if(rx>mid) query(p<<1|1,mid+1,r,lx,rx);
}
signed main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;i++) scanf("%d",&a[i]);
		build(1,1,n);
		while(m--){
			scanf("%d%d%d",&op,&l,&r);
			if(!op) scanf("%d",&v),modify(1,1,n,l,r,v);
			else
				Mx=Sum=0,query(1,1,n,l,r),printf("%lld\n",op==1?1ll*Mx:Sum);
		}
	}
	return 0;
}

A2

维护一个序列，支持：

• 修改：区间取 \(\min\)，区间加。
• 查询：区间求 \(\max\)，区间求和。

info：同 A1。

tag：\((add,tg)\) 表示先全 \(+add\)，再让 \(mx\) 对 \(tg\) 取 \(\min\)。

将 \(mx\) 当做 \(tg\) 下传，就不需记 \(tg\) 了。

\(mx2\leq v<mx\)，\(mx\) 对 \(v\) 取 \(\min\) 时：\(mx'\gets v\)，\(sum'\gets sum-(mx-v)\cdot cnt\)。

区间 \(+v\) 时：\(add'\gets add+v\)，\(sum'\gets sum+(r-l+1)v\)，\(mx'\gets mx+v\)，\(mx2'\gets mx2+v\)。

据说时间复杂度 \(\mathcal O(n\log n+m\log^2 n)\)，实战中表现近似于 \(\mathcal O((n+m)\log n)\)。

A3

BZOJ4695 最假女选手

维护一个序列，支持：

• 修改：区间取 \(\min\)，区间取 \(\max\)，区间加。
• 查询：区间求和，区间求 \(\max\)，区间求 \(\min\)。

info：区间最大值 \(mx\)，区间严格次大值 \(mx2\)，最大值出现次数 \(cmx\)；区间最小值 \(mn\)，区间严格次小值 \(mn2\)，最小值出现次数 \(cmn\)；区间和 \(sum\)。

tag：\((add,tgmx,tgmn)\) 表示先全 \(+add\)，再让 \(mx\) 对 \(tgmx\) 取 \(\min\)、\(mn\) 对 \(tgmn\) 取 \(\max\)。

将 \(mx\) 当做 \(tgmx\)，\(mn\) 当做 \(tgmn\) 下传，就不需要记 \(tgmx,tgmn\) 了，只需记 \(add\)。

\(mx2\leq v<mx\)，\(mx\) 对 \(v\) 取 \(\min\) 时：\(mx'\gets v\)，\(sum'\gets sum-(mx-v)cmx\)，并且当 \(mn=mx\) 时 \(mn'\gets v\)，当 \(mn2=mx\) 时 \(mn2'\gets v\)（但不影响 \(cmn\)）。

\(mn<v\leq mn2\)，\(mn\) 对 \(v\) 取 \(\max\) 时，\(mn'\gets v\)，\(sum'\gets sum'+(v-mn)\cdot cmn\)，并且当 \(mx=mn\) 时 \(mx'\gets v\)，当 \(mx2=mn\) 时 \(mx2'\gets v\)。

区间 \(+v\) 时：\(add'\gets add+v\)，\(mx'\gets mx+v\)，\(mx2'\gets mx2+v\)，\(mn'\gets mn+v\)，\(mn2'\gets mn2+v\)，\(sum'\gets sum+(r-l+1)v\)。

据说时间复杂度 \(\mathcal O(n\log n+m\log^2 n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,M=N<<2;
int n,m,a[N],op,l,r,v,mx[M],mx2[M],mn[M],mn2[M],cmx[M],cmn[M],Mx,Mn;
long long sum[M],add[M],Sum;
void push(int p){
	sum[p]=sum[p<<1]+sum[p<<1|1];
	mx[p]=max(mx[p<<1],mx[p<<1|1]);
	mx2[p]=max(mx[p]^mx[p<<1]?mx[p<<1]:mx2[p<<1],mx[p]^mx[p<<1|1]?mx[p<<1|1]:mx2[p<<1|1]);
	cmx[p]=(mx[p]==mx[p<<1]?cmx[p<<1]:0)+(mx[p]==mx[p<<1|1]?cmx[p<<1|1]:0);
	mn[p]=min(mn[p<<1],mn[p<<1|1]);
	mn2[p]=min(mn[p]^mn[p<<1]?mn[p<<1]:mn2[p<<1],mn[p]^mn[p<<1|1]?mn[p<<1|1]:mn2[p<<1|1]);
	cmn[p]=(mn[p]==mn[p<<1]?cmn[p<<1]:0)+(mn[p]==mn[p<<1|1]?cmn[p<<1|1]:0);
}
void build(int p,int l,int r){
	if(l==r){mx[p]=mn[p]=sum[p]=a[l],mx2[p]=-1e9,mn2[p]=1e9,cmx[p]=cmn[p]=1;return ;}
	int mid=(l+r)/2;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	push(p);
}
void updadd(int p,int l,int r,int v){	//p 对应区间 +v
	add[p]+=v,mx[p]+=v,mx2[p]+=v,mn[p]+=v,mn2[p]+=v,sum[p]+=1ll*(r-l+1)*v;
}
void updcmn(int p,int v){	//p 对应区间对 v 取 min，保证 mx2[p]<=v<mx[p]
	if(mn[p]==mx[p]) mn[p]=v;
	if(mn2[p]==mx[p]) mn2[p]=v;
	sum[p]-=1ll*(mx[p]-v)*cmx[p],mx[p]=v;
}
void updcmx(int p,int v){	//p 对应区间对 v 取 max，保证 mn[p]<v<=mn2[p]
	if(mx[p]==mn[p]) mx[p]=v;
	if(mx2[p]==mn[p]) mx2[p]=v;
	sum[p]+=1ll*(v-mn[p])*cmn[p],mn[p]=v;
}
void down(int p,int l,int r,int mid){
	if(add[p]) updadd(p<<1,l,mid,add[p]),updadd(p<<1|1,mid+1,r,add[p]),add[p]=0;
	if(mx[p]<mx[p<<1]) updcmn(p<<1,mx[p]);
	if(mx[p]<mx[p<<1|1]) updcmn(p<<1|1,mx[p]);
	if(mn[p]>mn[p<<1]) updcmx(p<<1,mn[p]);
	if(mn[p]>mn[p<<1|1]) updcmx(p<<1|1,mn[p]);
}
void mdfadd(int p,int l,int r,int lx,int rx,int v){
	if(l>=lx&&r<=rx) return updadd(p,l,r,v);
	int mid=(l+r)/2;
	down(p,l,r,mid);
	if(lx<=mid) mdfadd(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfadd(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void mdfcmn(int p,int l,int r,int lx,int rx,int v){
	if(mx[p]<=v) return ;
	if(l>=lx&&r<=rx&&mx2[p]<=v) return updcmn(p,v);
	int mid=(l+r)/2;
	down(p,l,r,mid);
	if(lx<=mid) mdfcmn(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfcmn(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void mdfcmx(int p,int l,int r,int lx,int rx,int v){
	if(v<=mn[p]) return ;
	if(l>=lx&&r<=rx&&v<=mn2[p]) return updcmx(p,v);
	int mid=(l+r)/2;
	down(p,l,r,mid);
	if(lx<=mid) mdfcmx(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfcmx(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void query(int p,int l,int r,int lx,int rx){
	if(l>=lx&&r<=rx){Mx=max(Mx,mx[p]),Mn=min(Mn,mn[p]),Sum+=sum[p];return ;}
	int mid=(l+r)/2;
	down(p,l,r,mid);
	if(lx<=mid) query(p<<1,l,mid,lx,rx);
	if(rx>mid) query(p<<1|1,mid+1,r,lx,rx);
}
signed main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(1,1,n);
	scanf("%d",&m);
	while(m--){
		scanf("%d%d%d",&op,&l,&r);
		if(op<=3)
			scanf("%d",&v),
			(op==1?mdfadd:(op==2?mdfcmx:mdfcmn))(1,1,n,l,r,v);
		else{
			Mx=-1e9,Mn=1e9,Sum=0,query(1,1,n,l,r);
			if(op==4) printf("%lld\n",Sum);
			else printf("%d\n",op==5?Mx:Mn);
		}
	}		
	return 0;
}

B1

维护两个序列 \(a,b\)，初始序列 \(b\) 全为 \(0\)。支持：

• 修改：对 \(a\) 区间取 \(\min\)，对 \(a\) 区间取 \(\max\)，对 \(a\) 区间加。
• 查询：查询 \(b\) 的区间和（每次操作完后，若 \(a_i\) 的值发生变化，就给 \(b_i\) 加 \(1\)。即 \(b_i\) 是 \(a_i\) 的成功 chkmax 次数）。

\(n,m\leq 3\times 10^5\)。

区间加：若 \(v\neq 0\)，给 \(b_i\) 区间 \(+1\)。

有了区间取 \(\min\)、区间取 \(\max\) 操作，本质上就是把线段树上一个节点的数分成三类——最大值、最小值、既不是最大值也不是最小值，然后对每一类数分别维护。

每次在 \(a\) 上 updcmn / updcmx 时就根据最大/小值个数在 \(b\) 上更新信息（不是给 \(b\) 打标记）。注意特判 \(mx=mn\) 的情况，避免重复贡献。

B2

两个序列 \(a,b\)，支持：

• 修改：对 \(a\) 区间取 \(\min\)，对 \(b\) 区间取 \(\min\)，对 \(a\) 区间加，对 \(b\) 区间加。
• 查询：查询区间 \(a_i+b_i\) 的最大值。

\(n,m\leq 3\times 10^5\)。

将线段树上一个节点的数分成四类——在 \(a\) 中“是/不是”区间最大值且在 \(b\) 中“是/不是”区间最大值。

对每类数分别维护区间中该类数的个数、答案的最大值。以及 \(a\) 的区间最大值/严格次大值，\(b\) 的区间最大值/严格次大值。

两个序列在操作中完全独立，两套标记之间并无影响，时间复杂度还是 \(\mathcal O((n+m)\log^2 n)\)。

扩展：对 \(k\) 个序列维护，只需将一个节点的树分成 \(2^k\) 类，时间复杂度 \(\mathcal O(2^k\cdot (n+m)\log^2 n)\)，空间复杂度 \(\mathcal O(2^k n)\)。

C1

灵活运用，来自 CF793F Julia the snail（*3000）

维护一个序列，支持：将一个区间所有 \(\geq x\) 的数改成 \(y\)，查询区间最大值。

info：区间最大值 \(mx\)，区间次大值 \(mx2\)。

• 若 \(mx<x\)，return。
• 若 \(mx2<x\leq mx\)，将所有 \(mx\) 改成 \(y\)。
• 若 \(x\leq mx2\)，递归。

CF855F Nagini（*3100）

2023.5.18

有 \(n=10^5\) 个集合，初始都为空。\(m\) 次操作：

• 1 l r v：在第 \([l,r)\) 个集合中加入 \(v\)。
• 2 l r：定义一个集合的权值为，若集合中同时存在 \(>0\) 和 \(<0\) 的数，则为“最小的 \(>0\) 的数”+“最大的 \(<0\) 的数的绝对值”，否则为 \(0\)。查询第 \([l,r)\) 个集合的权值和。

\(1\leq m\leq 5\times 10^4\)，\(-10^9\leq v\leq 10^9\land v\neq 0\)。

如果不管“同时存在 \(>0\) 和 \(<0\)”的限制，正数就是“初始所有值为 \(\infty\)，支持区间取 \(\min\)、区间非 \(\infty\) 部分求和”，负数取相反数后是一样的。

加上限制后，一个位置只有正负数对应的都 \(<\infty\) 才能计入答案。发现一个位置正负分别只会从 \(=\infty\) 变为 \(<\infty\) 一次。区间对 \(v\) 取 \(\min\) 时，若 \(mx2\leq v<mx\) 且 \(mx=\infty\)，就暴力重构整个区间子树的信息。

每个位置正负分别只会重构一次，这部分是 \(\mathcal O(n\log n)\) 的。总时间复杂度 \(\mathcal O((n+m)\log n)\)。

（代码实现非常妙。原来 \(cnt\) 表示最大值个数，现在改进一下——当存在正负是 \(\infty\) 时令 \(cnt=0\) 强制 upd 时不产生贡献。重构时就是把一个子树的叶子 \(mx\) 改掉并把 \(cnt\) 都改成 \(1\) 然后一路 pushup 上来）

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=N<<2;
int n=1e5,m,op,l,r,v,mx[2][M],mx2[2][M],cnt[2][M];
long long sum[M],Sum;
void push(int p){
	sum[p]=sum[p<<1]+sum[p<<1|1];
	for(int o=0;o<2;o++){
		int *m=mx[o],*m2=mx2[o],*c=cnt[o];
		m[p]=max(m[p<<1],m[p<<1|1]);
		m2[p]=max(m[p]^m[p<<1]?m[p<<1]:m2[p<<1],m[p]^m[p<<1|1]?m[p<<1|1]:m2[p<<1|1]);
		c[p]=(m[p]==m[p<<1]?c[p<<1]:0)+(m[p]==m[p<<1|1]?c[p<<1|1]:0);
	}
}
void upd(int o,int p,int v){
	sum[p]-=1ll*(mx[o][p]-v)*cnt[o][p],mx[o][p]=v;	//cnt>0 当且仅当正数负数都有了
}
void down(int p){
	for(int o=0;o<2;o++){
		if(mx[o][p]<mx[o][p<<1]) upd(o,p<<1,mx[o][p]);
		if(mx[o][p]<mx[o][p<<1|1]) upd(o,p<<1|1,mx[o][p]);
	}
}
void modify(int o,int p,int l,int r,int lx,int rx,int v){
	if(mx[o][p]<=v) return ;
	if(l>=lx&&r<=rx&&mx2[o][p]<=v){
		if(mx[o][p]<2e9) return upd(o,p,v);
		if(l==r){
			mx[o][p]=v;
			if(mx[o^1][p]<2e9) cnt[0][p]=cnt[1][p]=1,sum[p]=mx[0][p]+mx[1][p];	//只有正数负数都有了才令 cnt 有值
			return ;
		}
	}
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) modify(o,p<<1,l,mid,lx,rx,v);
	if(rx>mid) modify(o,p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void query(int p,int l,int r,int lx,int rx){
	if(l>=lx&&r<=rx){Sum+=sum[p];return ;}
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) query(p<<1,l,mid,lx,rx);
	if(rx>mid) query(p<<1|1,mid+1,r,lx,rx);
}
signed main(){
	scanf("%d",&m);
	for(int o=0;o<2;o++)
		fill(mx[o]+1,mx[o]+1+(n<<2),2e9);
	while(m--){
		scanf("%d%d%d",&op,&l,&r),r--;
		if(op==1) scanf("%d",&v),modify(v<0,1,1,n,l,r,abs(v));
		else Sum=0,query(1,1,n,l,r),printf("%lld\n",Sum);
	}
	return 0;
}

CF1290E Cartesian Tree（*3300）

2023.5.18

给出排列 \(a_{1\sim n}\)，对于所有 \(k\in[1,n]\)，查询所有 \(a_i\leq k\) 的项构成的子序列的“大根笛卡尔树的子树大小和”。

\(1\leq n\leq 1.5\times 10^5\)。

从小到大扫 \(k\)，每次插入 \(a_i=k\) 的项。

设 \(l_i,r_i\) 分别表示 \(i\) 左/右第一个 \(>a_i\) 的数在“已插入的子序列”中的位置，\(i\) 的子树就对应 \((l_i,r_i)\)，\(ans_k=\sum r_i-l_i-1\)。只需考虑怎么算 \(A=\sum r_i\)，然后把原序列翻转再算一次，得到的是 \(B=\sum_{i=1}^k k-l_i+1\)，\(ans_k=A+B-k(k+2)\)。

新插入 \(k\) 时，设 \(k\) 的位置是 \(pos\)。

• 对于 \((pos,n]\)：所有已插入项 \(r'\gets r+1\)。
• 对于 \(pos\)：从未插入改为已插入，\(r'\gets k+1\)。
• 对于 \([1,pos)\)：设 \(a_{pos}\) 在已插入项中的位置是 \(p\)，\(r'\gets \min(r,p)\)。

初始所有 \(r\) 为 \(0\)，支持区间 \(>0\) 的位置加，单点修改，区间取 \(\min\)。

时间复杂度 \(\mathcal O(n\log^2 n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=1.5e5+5,M=N<<2;
int n,a[N],pos[N],mx[M],mx2[M],cmx[M],cn0[M],add[M];	//cn0 表示区间中已插入数的个数
long long sum[M],res[N];
void push(int p){
	sum[p]=sum[p<<1]+sum[p<<1|1];
	mx[p]=max(mx[p<<1],mx[p<<1|1]);
	mx2[p]=max(mx[p]^mx[p<<1]?mx[p<<1]:mx2[p<<1],mx[p]^mx[p<<1|1]?mx[p<<1|1]:mx2[p<<1|1]);
	cmx[p]=(mx[p]==mx[p<<1]?cmx[p<<1]:0)+(mx[p]==mx[p<<1|1]?cmx[p<<1|1]:0);
	cn0[p]=cn0[p<<1]+cn0[p<<1|1];
}
void updadd(int p,int v){
	add[p]+=v,mx[p]+=v,mx2[p]+=v,sum[p]+=1ll*v*cn0[p];
}
void updcmn(int p,int v){
	sum[p]-=1ll*(mx[p]-v)*cmx[p],mx[p]=v;
}
void down(int p){
	if(add[p]) updadd(p<<1,add[p]),updadd(p<<1|1,add[p]),add[p]=0;
	if(mx[p]<mx[p<<1]) updcmn(p<<1,mx[p]);
	if(mx[p]<mx[p<<1|1]) updcmn(p<<1|1,mx[p]);
}
void mdfadd(int p,int l,int r,int lx,int rx,int v){
	if(l>=lx&&r<=rx) return updadd(p,v);
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) mdfadd(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfadd(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void mdfcmn(int p,int l,int r,int lx,int rx,int v){
	if(mx[p]<=v) return ;
	if(l>=lx&&r<=rx&&mx2[p]<=v) return updcmn(p,v);
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) mdfcmn(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfcmn(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void insert(int p,int l,int r,int pos,int v){
	if(l==r){mx[p]=sum[p]=v,cmx[p]=cn0[p]=1;return ;}
	int mid=(l+r)/2;
	down(p);
	if(pos<=mid) insert(p<<1,l,mid,pos,v);
	else insert(p<<1|1,mid+1,r,pos,v);
	push(p);
}
int qryn0(int p,int l,int r,int lx,int rx){
	if(l>=lx&&r<=rx) return cn0[p];
	int mid=(l+r)/2,ans=0;
	if(lx<=mid) ans=qryn0(p<<1,l,mid,lx,rx);
	if(rx>mid) ans+=qryn0(p<<1|1,mid+1,r,lx,rx);
	return ans;
}
void work(){
	for(int i=1;i<=n;i++) pos[a[i]]=i;
	for(int i=1;i<=(n<<2);i++) mx[i]=mx2[i]=-1e9,cmx[i]=cn0[i]=sum[i]=add[i]=0;
	for(int i=1;i<=n;i++){
		if(pos[i]<n) mdfadd(1,1,n,pos[i]+1,n,1);
		insert(1,1,n,pos[i],i+1);
		if(pos[i]>1) mdfcmn(1,1,n,1,pos[i]-1,qryn0(1,1,n,1,pos[i]));
		res[i]+=sum[1];
	}
}
signed main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	work(),reverse(a+1,a+1+n),work();
	for(int i=1;i<=n;i++)
		printf("%lld\n",res[i]-1ll*i*(i+2));
	return 0;
}

D1

P6242 【模板】线段树 3

维护一个序列，支持：

• 修改：区间加，区间取 \(\min\)。
• 查询：区间和，区间最大值，区间历史最大值的最大值。

根据 A2 要维护 \(\min\) 标记与加法标记，但可能会出现两种标记交替的情况，做不了历史的。

由于对 \(v\) 取 \(\min\) 时一定满足 \(mx2\leq v<mx\)，相当于区间内所有 \(=mx\) 的数加上 \(v-mx\)。

考虑对最大值和非最大值分别维护加法标记，\(tg\) 表示给区间内的 \(mx\) 加 \(tg\)，\(tg2\) 表示给区间内 \(mx\) 之外的数 \(+tg2\)。这样就处理掉了 \(\min\) 标记，只有加法标记了，沿用“五、A1”的做法即可。

（标记影响的对象不交，方便维护）

时间复杂度 \(\mathcal O(n\log n+m\log^2 n)\)。

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,M=N<<2;
int n,m,a[N],op,l,r,v,mx[M],mx2[M],hmx[M],cnt[M],Mx,hMx;
long long sum[M],Sum;
struct tag{
	int s,mxs;
	void upd(tag tg){mxs=max(mxs,s+tg.mxs),s+=tg.s;}
}tg[M],tg2[M];
void push(int p){
	sum[p]=sum[p<<1]+sum[p<<1|1];
	mx[p]=max(mx[p<<1],mx[p<<1|1]);
	mx2[p]=max(mx[p]^mx[p<<1]?mx[p<<1]:mx2[p<<1],mx[p]^mx[p<<1|1]?mx[p<<1|1]:mx2[p<<1|1]);
	cnt[p]=(mx[p]==mx[p<<1]?cnt[p<<1]:0)+(mx[p]==mx[p<<1|1]?cnt[p<<1|1]:0);
	hmx[p]=max(hmx[p<<1],hmx[p<<1|1]);
}
void build(int p,int l,int r){
	if(l==r){mx[p]=hmx[p]=sum[p]=a[l],mx2[p]=-2e9,cnt[p]=1;return ;}
	int mid=(l+r)/2;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	push(p);
}
void upd(int p,int l,int r,tag t1,tag t2){
	tg[p].upd(t1),tg2[p].upd(t2);
	sum[p]+=1ll*t1.s*cnt[p]+1ll*t2.s*(r-l+1-cnt[p]);
	hmx[p]=max(hmx[p],mx[p]+t1.mxs),mx[p]+=t1.s;
	if(mx2[p]>-2e9) mx2[p]+=t2.s;
}
void down(int p,int l,int r,int mid){
	int mx_=max(mx[p<<1],mx[p<<1|1]);
	upd(p<<1,l,mid,mx[p<<1]==mx_?tg[p]:tg2[p],tg2[p]),
	upd(p<<1|1,mid+1,r,mx[p<<1|1]==mx_?tg[p]:tg2[p],tg2[p]),
	tg[p]=tg2[p]={0,0};
}
void mdfadd(int p,int l,int r,int lx,int rx,int v){
	if(l>=lx&&r<=rx) return upd(p,l,r,{v,v},{v,v});
	int mid=(l+r)/2;
	down(p,l,r,mid);
	if(lx<=mid) mdfadd(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfadd(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void mdfcmn(int p,int l,int r,int lx,int rx,int v){
	if(mx[p]<=v) return ;
	if(l>=lx&&r<=rx&&mx2[p]<=v) return upd(p,l,r,{v-mx[p],v-mx[p]},{0,0});
	int mid=(l+r)/2;
	down(p,l,r,mid);
	if(lx<=mid) mdfcmn(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfcmn(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void query(int p,int l,int r,int lx,int rx){
	if(l>=lx&&r<=rx){Mx=max(Mx,mx[p]),hMx=max(hMx,hmx[p]),Sum+=sum[p];return ;}
	int mid=(l+r)/2;
	down(p,l,r,mid);
	if(lx<=mid) query(p<<1,l,mid,lx,rx);
	if(rx>mid) query(p<<1|1,mid+1,r,lx,rx);
}
signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(1,1,n);
	while(m--){
		scanf("%d%d%d",&op,&l,&r);
		if(op<=2)
			scanf("%d",&v),(op==1?mdfadd:mdfcmn)(1,1,n,l,r,v);
		else{
			Sum=0,Mx=hMx=-2e9,query(1,1,n,l,r);
			if(op==3) printf("%lld\n",Sum);
			else printf("%d\n",op==4?Mx:hMx);
		}
	}
	return 0;
}

D2

UOJ#170. Picks loves segment tree VIII

维护一个序列，支持：

• 修改：区间加，区间取 \(\min\)，区间取 \(\max\)。
• 查询：区间最小值，区间历史最小值的最小值，区间历史最大值的最大值。

三个加法标记 \(tmx,tmn,t\) 分别维护 \(mx\)、\(mn\)、非 \(mx\) 非 \(mn\) 的数要加多少。

注意改 \(mx\) 时可能会改 \(mn,mn2\)，改 \(mn\) 时可能会改 \(mx,mx2\)。

（题目不要求维护 \(sum\)，所以问题简单了很多）

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5,M=N<<2;
int n,m,a[N],op,l,r,v,mx[M],mx2[M],mn[M],mn2[M],hmx[M],hmn[M],Mn,hMn,hMx;
struct tag{
	int s,mxs,mns;
	void upd(tag tg){mxs=max(mxs,s+tg.mxs),mns=min(mns,s+tg.mns),s+=tg.s;}
}tmx[M],tmn[M],tg[M],tmp;
void push(int p){
	mx[p]=max(mx[p<<1],mx[p<<1|1]);
	mx2[p]=max(mx[p]^mx[p<<1]?mx[p<<1]:mx2[p<<1],mx[p]^mx[p<<1|1]?mx[p<<1|1]:mx2[p<<1|1]);
	mn[p]=min(mn[p<<1],mn[p<<1|1]);
	mn2[p]=min(mn[p]^mn[p<<1]?mn[p<<1]:mn2[p<<1],mn[p]^mn[p<<1|1]?mn[p<<1|1]:mn2[p<<1|1]);
	hmx[p]=max(hmx[p<<1],hmx[p<<1|1]);
	hmn[p]=min(hmn[p<<1],hmn[p<<1|1]);
}
void build(int p,int l,int r){
	if(l==r){mx[p]=mn[p]=hmx[p]=hmn[p]=a[l],mx2[p]=-2e9-1,mn2[p]=2e9+1;return ;}
	int mid=(l+r)/2;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	push(p);
}
void upd(int p,tag t1,tag t2,tag t3){
	tmx[p].upd(t1),tmn[p].upd(t2),tg[p].upd(t3);
	if(mx2[p]>=-2e9) mx2[p]+=mx2[p]==mn[p]?t2.s:t3.s;	//!!! 某 sb 把这一行和下一行放到了 upd 的最后，但最后 mx[p],mn[p] 都已被修改，导致误判
	if(mn2[p]<=2e9) mn2[p]+=mn2[p]==mx[p]?t1.s:t3.s;
	hmx[p]=max(hmx[p],mx[p]+t1.mxs),mx[p]+=t1.s;
	hmn[p]=min(hmn[p],mn[p]+t2.mns),mn[p]+=t2.s;
}
void down(int p){
	int mx_=max(mx[p<<1],mx[p<<1|1]),mn_=min(mn[p<<1],mn[p<<1|1]);
	auto o=[&](int v){return v==mx_?tmx[p]:(v==mn_?tmn[p]:tg[p]);};
	upd(p<<1,o(mx[p<<1]),o(mn[p<<1]),tg[p]);
	upd(p<<1|1,o(mx[p<<1|1]),o(mn[p<<1|1]),tg[p]);
	tmx[p]=tmn[p]=tg[p]={0,0,0};
}
void mdfadd(int p,int l,int r,int lx,int rx,int v){
	if(l>=lx&&r<=rx) return upd(p,{v,v,v},{v,v,v},{v,v,v});
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) mdfadd(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfadd(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void mdfcmn(int p,int l,int r,int lx,int rx,int v){
	if(mx[p]<=v) return ;
	if(l>=lx&&r<=rx&&mx2[p]<=v)
		return tmp={v-mx[p],v-mx[p],v-mx[p]},upd(p,tmp,mx[p]==mn[p]?tmp:(tag){0,0,0},{0,0,0});
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) mdfcmn(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfcmn(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void mdfcmx(int p,int l,int r,int lx,int rx,int v){
	if(v<=mn[p]) return ;
	if(l>=lx&&r<=rx&&v<=mn2[p])
		return tmp={v-mn[p],v-mn[p],v-mn[p]},upd(p,mx[p]==mn[p]?tmp:(tag){0,0,0},tmp,{0,0,0});
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) mdfcmx(p<<1,l,mid,lx,rx,v);
	if(rx>mid) mdfcmx(p<<1|1,mid+1,r,lx,rx,v);
	push(p);
}
void query(int p,int l,int r,int lx,int rx){
	if(l>=lx&&r<=rx){Mn=min(Mn,mn[p]),hMn=min(hMn,hmn[p]),hMx=max(hMx,hmx[p]);return ;}
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) query(p<<1,l,mid,lx,rx);
	if(rx>mid) query(p<<1|1,mid+1,r,lx,rx);
}
signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	build(1,1,n);
	while(m--){
		scanf("%d%d%d",&op,&l,&r);
		if(op==1||op==2||op==5)
			scanf("%d",&v),(op==1?mdfadd:(op==2?mdfcmx:mdfcmn))(1,1,n,l,r,v);
		else
			Mn=hMn=2e9,hMx=-2e9,query(1,1,n,l,r),
			printf("%d\n",op==3?Mn:(op==4?hMn:hMx));
	}
	return 0;
}

UOJ#164. 【清华集训2015】V

2023.5.19

维护一个序列，支持：

• 修改：区间加，区间减并对 \(0\) 取 \(\max\)，区间赋值。
• 查询：单点值，单点历史最大值。

直接套 seg-beats 2log 较慢。

可以将所有修改转化为先 \(+x\) 再立刻对 \(y\) 取 \(\max\)，三种修改分别是 \((v,-\infty),(-v,0),(-\infty,v)\)。

标记 \((x,y)\) 表示这个区间先 \(+x\) 再立刻对 \(v\) 取 \(\max\)。

\[v'=\max(\max(v+x_1,y_1)+x_2,y_2)=\max(v+x_1+x_2,\max(y_1+x_2,y_2))\\ \Rightarrow (x_1,y_1)+(x_2,y_2)=(x_1+x_2,\max(y_1+x_2,y_2)) \]

然后考虑维护历史值。

\[hmx_v=\max(\max(v+x_1,y_1),\max(v+x_1+x_2,-y_1+x_2,y_2))\\ =\max(v+\max(x_1,x_1+x_2),\max(y_1,\max(y_1+x_2,y_2))) \]

多维护 \(hx,hy\) 即可。想象一下两个标记队列合并的过程。

时间复杂度 \(\mathcal O(m\log n)\)。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e5+5,M=N<<2;
int n,m,a[N],op,l,r,v,x;
ll inf=1e18;
struct tag{
	ll x,y,hx,hy;
	void upd(tag tg){
		hx=max(hx,x+tg.hx),hy=max({hy,y+tg.hx,tg.hy});
		x+=tg.x,x=max(x,-inf),y=max(y+tg.x,tg.y);	//!!! 对 -inf 取 max，避免爆 ll
	}
}tg[M];
void down(int p){
	tg[p<<1].upd(tg[p]),tg[p<<1|1].upd(tg[p]),tg[p]={0,0,0,0};
}
void modify(int p,int l,int r,int lx,int rx,tag v){
	if(l>=lx&&r<=rx) return tg[p].upd(v);
	int mid=(l+r)/2;
	down(p);
	if(lx<=mid) modify(p<<1,l,mid,lx,rx,v);
	if(rx>mid) modify(p<<1|1,mid+1,r,lx,rx,v);
}
void query(int p,int l,int r,int pos){
	if(l==r){printf("%lld\n",op==4?max(a[l]+tg[p].x,tg[p].y):max(a[l]+tg[p].hx,tg[p].hy));return ;}
	int mid=(l+r)/2;
	down(p);
	if(pos<=mid) query(p<<1,l,mid,pos);
	else query(p<<1|1,mid+1,r,pos);
}
signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	while(m--){
		scanf("%d",&op);
		if(op<=3)
			scanf("%d%d%d",&l,&r,&v),
			modify(1,1,n,l,r,op==1?(tag){v,-inf,v,-inf}:(op==2?(tag){-v,0,-v,0}:(tag){-inf,v,-inf,v}));
		else
			scanf("%d",&x),query(1,1,n,x);
	}
	return 0;
}

七、zkw 线段树

用于优化在线段树上的遍历速度。比如单点取 \(\min\)，区间查 \(\min\)，树状数组做不了，zkw 比普通线段树快，可以卡常。

有些不会的可以写普通线段树的递归，会的那些写 zkw 版的遍历。

结构

除了底层都补满。原序列 \(a\) 在底层，且左右两边需要两个哨兵节点（用于区间查询）。

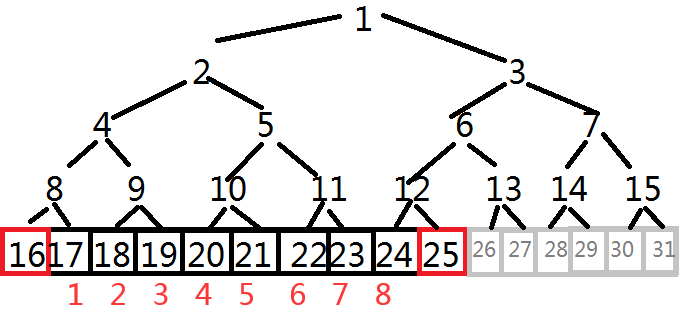
设 \(1\) 的深度为 \(0\)，底层的深度为 \(d\)。底层上面有 \(2^0+2^1+\cdots+2^{d-1}=2^d-1\) 个点，底层有 \(n+2\) 个点（需要满足 \(2^d\geq n+2\)。取最小的使得 \(2^d\geq n+2\) 的 \(d\) 即可）。

• \(a_i\) 在线段树中的编号恰好为 \((2^d-1)+(1+i)=2^d+i\)。
• 对于编号为 \(p\) 的节点：
  • 其父亲为 p>>1。进一步，其 \(k\) 级祖先为 p>>k。
  • 其儿子为 p<<1、p<<1|1。
  • 若 !(p&1)，则其为父亲的左儿子，否则为其父亲的右儿子。
  • 其兄弟为 p^1。

建树：写成 \(L=2^d\) 更方便。

for(L=1;L<n+2;L<<=1);
for(int i=1;i<=n;i++) scanf("%d",&s[L+i]);
for(int p=(L+n)>>1;p;p--) s[p]=s[p<<1]+s[p<<1|1];

单点修改

单点修改：

void modify(int p,int v){
	s[p+=L]+=v;
	for(p>>=1;p;p>>=1) s[p]=s[p<<1]+s[p<<1|1];
}

优化：往上更新时，若更新不动了或没必要更新时，就直接 break，不用遍历到根。普通线段树则无法实现这个优化。听说某些特殊题目加上这个优化可以实现势能 zkw 线段树。

单点查询：

void query(int p){
	for(p+=L;p;p>>=1) ans+=s[p];
}

区间查询：

void query(int l,int r){
	for(l+=L-1,r+=L+1;l^1^r;l>>=1,r>>=1){
		if(!(l&1)) ans+=s[l^1];
		if(r&1) ans+=s[r^1];
	}
}

区间修改

注意区间修改 \(\text{lca}\) 到根的链也需要 push。

标记永久化

注意，down 打标记只要标记有结合律就行了，而标记永久化还需要满足标记有交换律。

例如区间加，区间求 \(\max\)。

tg[p] 表示 \(p\) 的所有子孙（不包括 \(p\) 自己）都需要 +tg[p]。

#define push(p) mx[p]=max(mx[p<<1],mx[p<<1|1])+tg[p]
void modify(int l,int r,int v){
	for(l+=L-1,r+=L+1;l^1^r;){
		if(!(l&1)) mx[l^1]+=v,tg[l^1]+=v;
		if(r&1) mx[r^1]+=v,tg[r^1]+=v;
		l>>=1,r>>=1,push(l),push(r);
	}
	for(l>>=1;l;l>>=1) push(l);
}
int query(int l,int r){
	int mxl=0,mxr=0;
	for(l+=L-1,r+=L+1;l^1^r;){
		if(!(l&1)) mxl=max(mxl,mx[l^1]);
		if(r&1) mxr=max(mxr,mx[r^1]);
		l>>=1,r>>=1,mxl+=tg[l],mxr+=tg[r];
	}
	mxl=max(mxl,mxr);
	for(l>>=1;l;l>>=1) mxl+=tg[l];
	return mxl;
}

区间加，区间求和：

#define push(p) s[p]=s[p<<1]+s[p<<1|1]+tg[p]*len
void modify(int l,int r,ll v){
	int len=1;
	for(l+=L-1,r+=L+1;l^1^r;){
		if(!(l&1)) s[l^1]+=v*len,tg[l^1]+=v;
		if(r&1) s[r^1]+=v*len,tg[r^1]+=v;
		l>>=1,r>>=1,len<<=1,push(l),push(r);
	}
	for(l>>=1,len<<=1;l;l>>=1,len<<=1) push(l);
}
ll query(int l,int r){
	ll ans=0;
	int len=1,szl=0,szr=0;
	for(l+=L-1,r+=L+1;l^1^r;){
		if(!(l&1)) ans+=s[l^1],szl+=len;
		if(r&1) ans+=s[r^1],szr+=len;
		l>>=1,r>>=1,len<<=1,
		ans+=tg[l]*szl+tg[r]*szr;
	}
	szl+=szr;
	for(l>>=1,len<<=1;l;l>>=1,len<<=1) ans+=tg[l]*szl;
	return ans;
}

如果只是区间加，单点查询的话，由于不需要区间求和，维护 sum 没有意义。每次单点查询时，从叶子往上把所有 tg 加起来就行了。

void modify(int l,int r,int v){
	for(l+=L-1,r+=L+1;l^1^r;l>>=1,r>>=1){
		if(!(l&1)) tg[l^1]+=v;
		if(r&1) tg[r^1]+=v;
	}
}
int query(int p){
	int ans=a[p];
	for(p+=L;p;p>>=1) ans+=tg[p];
	return ans;
}

下传标记

实际上直接打标

实际上直接打标记也是可以的。不过速度貌似与普通线段树差不多。

例如区间加，区间求和：

void push(int p){
	s[p]=s[p<<1]+s[p<<1|1];
}
void upd(int p,ll v){
	tg[p]+=v,s[p]+=len[p]*v;
}
void down(int p){
	if(tg[p]) upd(p<<1,tg[p]),upd(p<<1|1,tg[p]),tg[p]=0;
}
void modify(int l,int r,ll v){
	l+=L-1,r+=L+1;
	for(int i=d;i>=0;i--) down(l>>i),down(r>>i);
	for(;l^1^r;push(l>>=1),push(r>>=1)){
		if(!(l&1)) upd(l^1,v);
		if(r&1) upd(r^1,v);
	}
	for(l>>=1;l;l>>=1) push(l);
}
ll query(int l,int r){
	l+=L-1,r+=L+1;
	for(int i=d;i>=0;i--) down(l>>i),down(r>>i);
	ll ans=0;
	for(;l^1^r;l>>=1,r>>=1){
		if(!(l&1)) ans+=s[l^1];
		if(r&1) ans+=s[r^1];
	}
	return ans;
}
signed main(){
	for(L=1;L<n+2;L<<=1,d++);
	for(int i=1;i<=n;i++)
		scanf("%lld",&s[L+i]),len[L+i]=1;
	for(int p=(L+n)>>1;p;p--)
		push(p),len[p]=len[p<<1]+len[p<<1|1];
}

zkw 线段树二分

到最底层才能知道具体位置。

比如求从右往左第一个 \(>0\) 的位置。从上往下找。

int find(){
	for(int p=1,stg=0;p<=L+n;){
		if(p>L) return s[p]+stg>0?p-L:-1;
		stg+=tg[p];
		if(s[p<<1|1]+stg>0) p=p<<1|1;
		else p<<=1;
	}
}

八、线段树结构

区间定位数：\([l,r]\) 最少拆成多少线段树节点的并。

对于 \([1,n]\) 的广义线段树：（注意广义线段树不能直接 p<<1,p<<1|1 分配编号）

• \([l,r]\) 的区间定位数 = 完全 \(\subseteq [l,r]\) 的点构成的完满二叉树森林的根的数量 = \(2\times (r-l+1)-\) 完全 \(\subseteq [l,r]\) 的线段树节点数。

  一棵完满二叉树的节点数 \(=n_0+n_1+n_2=n_0+0+(n_0-1)=2n_0-1\)。

  总节点数 \(=\sum (2n_0-1)=(2\sum n_0)-\sum 1=2(r-l+1)-\) 根个数。

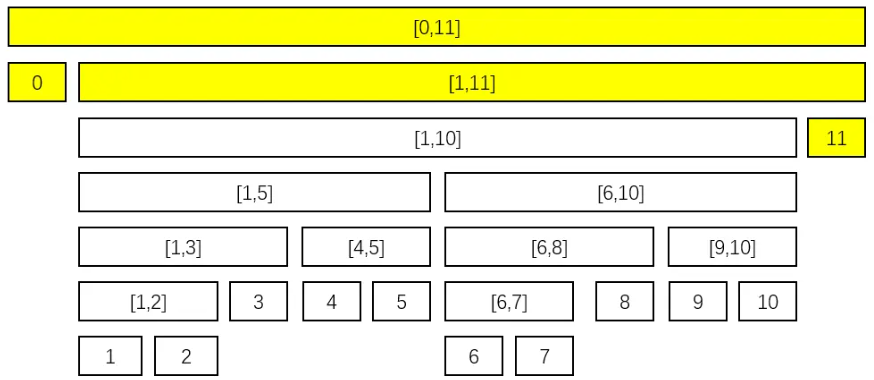
• 记 \([l-1,l-1],[r+1,r+1]\) 对应节点分别为 \(L,R\)、\(U=\text{lca}(L,R)\)，那么 \([l,r]\) 的区间定位由以下两部分组成：

  1. \(L\leadsto lc_U\) 的链上，所有左儿子对应的右兄弟。

  即，所有父亲在链上且为其父亲左儿子的点对应的右兄弟。

2. \(R\leadsto rc_U\) 的链上，所有右儿子对应的左兄弟。

   即，所有父亲在链上且为其父亲右儿子的点对应的左兄弟。

简单来讲，就是 \(L\leadsto U,R\leadsto U\) 包围住的点恰好就是要查询的区间。从 \(L\) 往父亲走，每当 \(L\) 为其父亲的左儿子时，其兄弟一定在区间里；从 \(R\) 往父亲走，每当 \(R\) 为其父亲的右儿子时，其兄弟也一定在区间里。这个可以应用到 zkw 线段树的区间查询中。

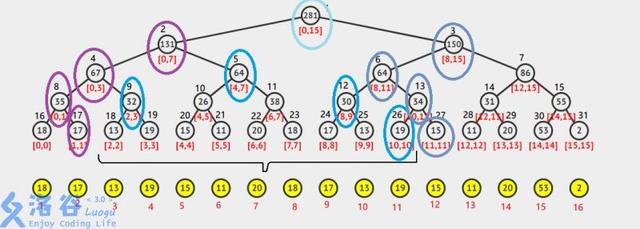
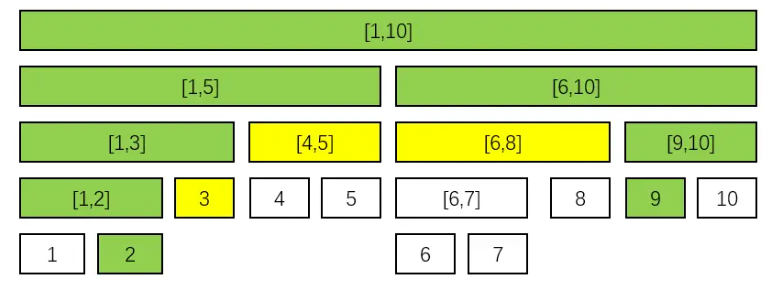
P5210 [ZJOI2017] 线段树

2024.1.6

给出 \([1,n]\) 的广义线段树，\(m\) 次询问：

• x l r：求线段树上节点 \(x\) 到所有“\([l,r]\) 的区间定位节点”的距离和。

\(2\leq n\leq 2\times 10^5\)，\(1\leq m\leq 2\times 10^5\)。

使用 zkw 的哨兵思想，记 \([l-1,l-1],[r+1,r+1]\) 对应节点分别为 \(L,R\)、\(U=\text{lca}(L,R)\)，那么 \([l,r]\) 的区间定位有：

1. \(L\leadsto lc_U\) 的链中，所有左儿子对应的右兄弟。

   即，所有父亲在链上且为其父亲左儿子的点对应的右兄弟。

2. \(R\leadsto rc_U\) 的链中，所有右儿子对应的左兄弟。

   即，所有父亲在链上且为其父亲右儿子的点对应的左兄弟。

以 1 为例，2 同理。先差分，转化为形如求：\(x\) 到“\(L\leadsto rt\) 的链中左儿子对应的右兄弟”的距离和。

\[\sum_{i\in S}dis(i,x)=dep_x|S|+\sum_{i\in S}dep_i-2\sum_{i\in S}dep_{\text{lca}(i,x)} \]

其中，\(L\leadsto rt\) 的链中的左儿子有多少右兄弟 \(cnt\)（\(|S|\)），这些右兄弟的 \(dep\) 之和 \(sum\)（\(\sum_{i\in S}dep_i\)），都可以前缀和求出。\(cnt_{lc_p}\gets cnt_p+1\)，\(cnt_{rc_p}\gets cnt_p\)，\(sum_{lc_p}\gets sum_p+dep_{rc_p}\)，\(sum_{rc_p}\gets sum_p\)。

对于 \(\text{lca}(i,x)\)（\(i\) 的左兄弟在 \(L\leadsto rt\) 上），需要分类讨论：记 \(p=\text{lca}(L,x)\)。

• 若 \(dep_{fa_i}>dep_p\)，则 \(\text{lca}(i,x)=p\)。

• 若 \(dep_{fa_i}=dep_p\)：

  若 \(i\) 合法，则一定有 \(L\in subtree(lc_p)\)（\(i\) 的左兄弟在链上）。故 \(x\in subtree(rc_p)\cup\{p\}\)（\(\text{lca}(L,x)=p\)）。此时，若 \(x\in subtree(rc_p)\)，则 \(\text{lca}(i,x)=i\)；否则 \(x=p\)，\(\text{lca}(i,x)=p\)。

• 若 \(dep_{fa_i}<dep_p\)，则 \(\text{lca}(i,x)=fa_i\)。

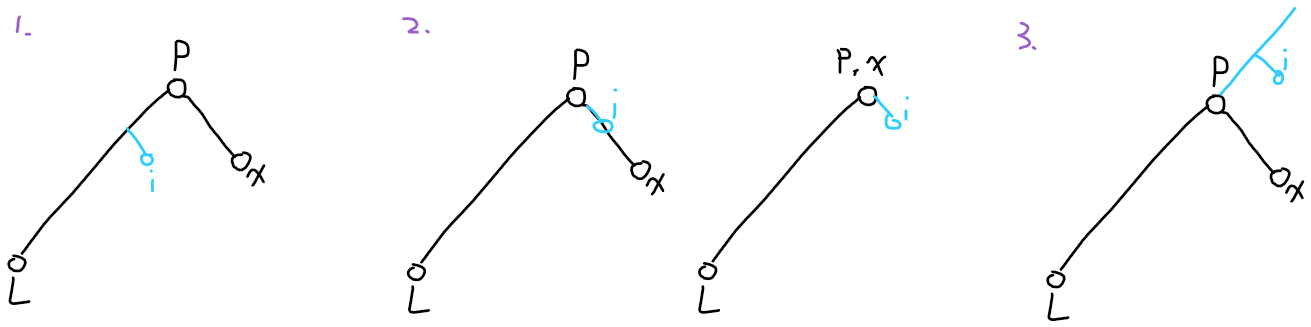
故：

\[\sum_{i\in S}dep_{\text{lca}(i,x)}=dep_p(cnt_L-cnt_p)+[L\in subtree(lc_p)\land x\neq p]+sum_p-cnt_p \]

时间复杂度 \(\mathcal O(n\log n)\)。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=4e5+5;
int n,m,x,l,r,U,rt,tot,id[N],lc[N],rc[N],cnt[N][2],f[N][25],dep[N];
ll sum[N][2],ans;
void build(int &p,int l,int r){
	p=++tot;
	if(l==r){id[l]=p;return ;}
	int mid;
	scanf("%d",&mid);
	build(lc[p],l,mid);
	build(rc[p],mid+1,r);
}
void dfs(int x){
	for(int i=0;i<=19;i++) f[x][i+1]=f[f[x][i]][i];
	int l=lc[x],r=rc[x];
	if(!l) return ;
	dep[l]=dep[r]=dep[x]+1,f[l][0]=f[r][0]=x;
	cnt[l][0]=cnt[x][0],sum[l][0]=sum[x][0];
	cnt[l][1]=cnt[x][1]+1,sum[l][1]=sum[x][1]+dep[r];
	cnt[r][0]=cnt[x][0]+1,sum[r][0]=sum[x][0]+dep[l];
	cnt[r][1]=cnt[x][1],sum[r][1]=sum[x][1];
	dfs(l),dfs(r);
}
int lca(int x,int y){
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=20;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
	if(x==y) return x;
	for(int i=20;i>=0;i--)
		if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
	return f[x][0];
}
ll suml(int L){
	int p=lca(L,x);
	ll s=1ll*dep[p]*(cnt[L][1]-cnt[p][1])+sum[p][1]-cnt[p][1];
	if(lca(L,lc[p])==lc[p]&&x!=p) s++;
	return 1ll*dep[x]*cnt[L][1]+sum[L][1]-2*s;
}
ll sumr(int R){
	int p=lca(R,x);
	ll s=1ll*dep[p]*(cnt[R][0]-cnt[p][0])+sum[p][0]-cnt[p][0];
	if(lca(R,rc[p])==rc[p]&&x!=p) s++;
	return 1ll*dep[x]*cnt[R][0]+sum[R][0]-2*s;
}
signed main(){
	scanf("%d",&n);
	build(rt,1,n),dep[1]=1,dfs(1);
	scanf("%d",&m);
	while(m--){
		scanf("%d%d%d",&x,&l,&r),ans=0;
		if(l==1&&r==n) ans=dep[x]-1;
		else{
			if(l>1) ans+=suml(id[l-1]);
			if(r<n) ans+=sumr(id[r+1]);
			if(l>1&&r<n)
				U=lca(id[l-1],id[r+1]),ans-=suml(lc[U])+sumr(rc[U]);
		}
		printf("%lld\n",ans);
	}
	return 0;
}

九、modify 影响

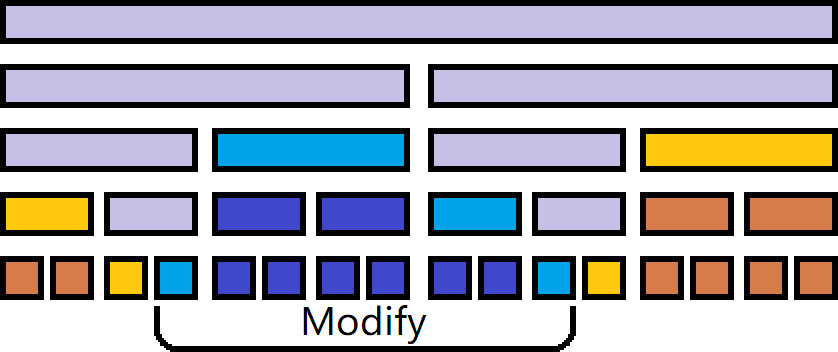
一个点 \([l,r]\) 与 modify 区间 \([ql,qr]\) 的关系有三种：

• \([l,r]\subseteq[ql,qr]\)：称为全 cover。
• \([l,r]\cap[ql,qr]\neq \varnothing\) 且 \([l,r]\not\subseteq [ql,qr]\)：称为半 cover。
• \([l,r]\cap[ql,qr]=\varnothing\)：称为无 cover。

进一步：

• 全 cover 的父亲可能是半 cover 或全 cover，只有其父亲是半 cover 时才会 upd 它。
• 半 cover 的父亲一定是半 cover，会 pushdown 它。
• 无 cover 的父亲可能是半 cover 或无 cover，只有其父亲是半 cover 时才会得到祖先 pushdown 来的 tag。

于是分为 5 类点。设 \(f_x\) 表示节点 \(x\) 是否有 tag，\(g_x\) 表示 \(x\) 到根链上是否有 tag。

1. 浅蓝：全 cover 且其父亲半 cover，会 upd 它，操作后必然有 tag。

   \(f_x'\gets 1\)，\(g_x'\gets 1\)。

2. 深蓝：全 cover 且其父亲也全 cover。它的祖先中必然有 1 类点，它的祖先中必然有 tag。

   \(f_x'\gets f_x\)，\(g_x'\gets 1\)。

3. 紫：半 cover，会 pushdown 它，操作后必然无 tag。它的祖先也必然无 tag。

   \(f_x'\gets 0\)，\(g_x'\gets 0\)。

4. 黄：无 cover 且其父亲半 cover，操作后有无 tag 取决于操作前它到根链上是否有 tag。

   \(f'_x\gets g_x\)，\(g_x'\gets g_x\)。

5. 橙：无 cover 且其父亲无 cover，不变。

   \(f'_x\gets f_x\)，\(g'_x\gets g_x\)。

void modify(int p,int l,int r,int lx,int rx){
	if(l>rx||r<lx){	//4 类点
		if(l!=r) //p<<1,p<<1|1 是 5 类点
		return ;
	}
	if(l>=lx&&r<=rx){	//1 类点
		(f[p]+=pw)%=mod,(g[p]+=pw)%=mod;
		if(l!=r)	//p<<1,p<<1|1 是 2 类点
		return ;
	}
	int mid=(l+r)/2;
	down(p);	//3 类点
	modify(p<<1,l,mid,lx,rx);
	modify(p<<1|1,mid+1,r,lx,rx);
}

P5280 [ZJOI2019] 线段树

2024.1.7 同 UOJ#467. 【ZJOI2019】线段树、LOJ#3043. 「ZJOI2019」线段树

初始有一棵什么标记都没有的 \([1,n]\) 上的线段树。\(m\) 次操作：

• 1 l r：将当前所有的线段树都复制一份，然后对新增线段树执行一次 modify \([l,r]\)。
• 2：求所有线段树中 tag 为 \(1\) 的节点总数 \(\bmod 998244353\)。

\(1\leq n,m\leq 10^5\)。

一个点 \([l,r]\) 与 modify 区间 \([ql,qr]\) 的关系有三种：

• \([l,r]\subseteq[ql,qr]\)：称为全 cover。
• \([l,r]\cap[ql,qr]\neq \varnothing\) 且 \([l,r]\not\subseteq [ql,qr]\)：称为半 cover。
• \([l,r]\cap[ql,qr]=\varnothing\)：称为无 cover。

进一步：

• 全 cover 的父亲可能是半 cover 或全 cover，只有其父亲是半 cover 时才会 upd 它。
• 半 cover 的父亲一定是半 cover，会 pushdown 它。
• 无 cover 的父亲可能是半 cover 或无 cover，只有其父亲是半 cover 时才会得到祖先 pushdown 来的 tag。

于是分为 5 类点。设 \(f_x\) 表示节点 \(x\) 是否有 tag，\(g_x\) 表示 \(x\) 到根链上是否有 tag。

1. 浅蓝：全 cover 且其父亲半 cover，会 upd 它，操作后必然有 tag。

   \(f_x'\gets 1\)，\(g_x'\gets 1\)。

2. 深蓝：全 cover 且其父亲也全 cover。它的祖先中必然有 1 类点，它的祖先中必然有 tag。

   \(f_x'\gets f_x\)，\(g_x'\gets 1\)。

3. 紫：半 cover，会 pushdown 它，操作后必然无 tag。它的祖先也必然无 tag。

   \(f_x'\gets 0\)，\(g_x'\gets 0\)。

4. 黄：无 cover 且其父亲半 cover，操作后有无 tag 取决于操作前它到根链上是否有 tag。

   \(f'_x\gets g_x\)，\(g_x'\gets g_x\)。

5. 橙：无 cover 且其父亲无 cover，不变。

   \(f'_x\gets f_x\)，\(g'_x\gets g_x\)。

void modify(int p,int l,int r,int lx,int rx){
	if(l>rx||r<lx){	//4 类点
		if(l!=r) //p<<1,p<<1|1 是 5 类点
		return ;
	}
	if(l>=lx&&r<=rx){	//1 类点
		(f[p]+=pw)%=mod,(g[p]+=pw)%=mod;
		if(l!=r)	//p<<1,p<<1|1 是 2 类点
		return ;
	}
	int mid=(l+r)/2;
	down(p);	//3 类点
	modify(p<<1,l,mid,lx,rx);
	modify(p<<1|1,mid+1,r,lx,rx);
}

对于第 \(i\) 次操作 1，操作前有 \(2^{i-1}\) 棵线段树，操作后会新增 \(2^{i-1}\) 棵，共 \(2^i\) 棵。设 \(sf_x\) 表示所有线段树的 \(f_x\) 之和，\(sg_x\) 表示所有线段树的 \(g_x\) 之和。\(ans=\sum_x sf_x\)。

1. \(sf_x'\gets sf_x+2^{i-1}\)，\(sg_x'\gets sg_x+2^{i-1}\)。
2. \(sf_x'\gets sf_x\times 2\)，\(sg_x'\gets sg_x+2^{i-1}\)。
3. \(sf_x'\gets sf_x\)，\(sg_x'\gets sg_x\)。
4. \(sf_x'\gets sf_x+sg_x\)，\(sg_x'\gets sg_x\times 2\)。
5. \(sf_x'\gets sf_x\times 2\)，\(sg_x'\gets sg_x\times 2\)。

1,3,4 可以暴力改，2,5 需要打标记改。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=N<<3,mod=998244353;	//!!! 数组要开大，因为偷懒写了 叶子<<1 叶子<<1|1
int n,m,op,l,r,f[M],g[M],mf[M],mg[M],ag[M],sum[M],pw=1;
void push(int p){
	sum[p]=(0ll+sum[p<<1]+sum[p<<1|1]+f[p])%mod;	//!!! 0ll+
}
void mulf(int p,int v){
	mf[p]=1ll*mf[p]*v%mod;
	f[p]=1ll*f[p]*v%mod,sum[p]=1ll*sum[p]*v%mod;
}
void mulg(int p,int v){
	mg[p]=1ll*mg[p]*v%mod,ag[p]=1ll*ag[p]*v%mod;
	g[p]=1ll*g[p]*v%mod;
}
void addg(int p,int v){
	(ag[p]+=v)%=mod,(g[p]+=v)%=mod;
}
void down(int p){
	mulf(p<<1,mf[p]),mulf(p<<1|1,mf[p]),mf[p]=1;
	mulg(p<<1,mg[p]),mulg(p<<1|1,mg[p]),mg[p]=1;
	addg(p<<1,ag[p]),addg(p<<1|1,ag[p]),ag[p]=0;
}
void modify(int p,int l,int r,int lx,int rx){
	down(p);	//!!! 在给 p<<1,p<<1|1 打标记前要先 down(p)
	if(l>rx||r<lx){
		(f[p]+=g[p])%=mod,g[p]=2ll*g[p]%mod;
		mulf(p<<1,2),mulg(p<<1,2),mulf(p<<1|1,2),mulg(p<<1|1,2);
		return push(p);
	}
	if(l>=lx&&r<=rx){
		(f[p]+=pw)%=mod,(g[p]+=pw)%=mod;
		mulf(p<<1,2),addg(p<<1,pw),mulf(p<<1|1,2),addg(p<<1|1,pw);
		return push(p);
	}
	int mid=(l+r)/2;
	modify(p<<1,l,mid,lx,rx);
	modify(p<<1|1,mid+1,r,lx,rx);
	push(p);
}
signed main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=(n<<2);i++) mf[i]=mg[i]=1;
	for(int i=1;i<=m;i++){
		scanf("%d",&op);
		if(op==1)
			scanf("%d%d",&l,&r),modify(1,1,n,l,r),pw=2ll*pw%mod;
		else printf("%d\n",sum[1]);
	}
	return 0;
}

P6630 [ZJOI2020] 传统艺能

2024.1.8 同 UOJ#585. 【ZJOI2020】传统艺能、LOJ#3312. 「ZJOI2020」传统艺能

给出一棵 \([1,n]\) 的广义线段树，每次操作等概率选一个 \([l,r]\) 进行 modify。问 \(k\) 次操作后期望有多少个点 \(tag\) 为 \(1\)。答案对 \(998244353\) 取模。

\(1\leq n\leq 2\times 10^5\)，\(1\leq k\leq 10^9\)。

根据 P5280 [ZJOI2019] 线段树 的套路：

设 \(f_x\) 表示节点 \(x\) 是否有 tag，\(g_x\) 表示 \(x\) 到根链上是否有 tag。

1. 浅蓝：全 cover 且其父亲半 cover，会 upd 它，操作后必然有 tag。

   \(f_x'\gets 1\)，\(g_x'\gets 1\)。

2. 深蓝：全 cover 且其父亲也全 cover。它的祖先中必然有 1 类点，它的祖先中必然有 tag。

   \(f_x'\gets f_x\)，\(g_x'\gets 1\)。

3. 紫：半 cover，会 pushdown 它，操作后必然无 tag。它的祖先也必然无 tag。

   \(f_x'\gets 0\)，\(g_x'\gets 0\)。

4. 黄：无 cover 且其父亲半 cover，操作后有无 tag 取决于操作前它到根链上是否有 tag。

   \(f'_x\gets g_x\)，\(g_x'\gets g_x\)。

5. 橙：无 cover 且其父亲无 cover，不变。

   \(f'_x\gets f_x\)，\(g'_x\gets g_x\)。

设 \(p1_x,p2_x,\cdots,p5_x\) 分别表示 \(x\) 是第 1/2/3/4/5 类点的概率。可以 \(\mathcal O(1)\) 算：

• 设 \(x\) 代表区间 \([l,r]\)，\(fa_x\) 代表 \([L,R]\)。

  \(p1_x\)：\(x\) 全 cover 的概率 - \(fa_x\) 全 cover 的概率。

  \(p2_x\)：\(fa_x\) 全 cover 的概率。

  \(p3_x\)：\(x\) 半 cover 的概率。

  \(p4_x\)：\(x\) 无 cover 的概率 - \(fa_x\) 无 cover 的概率。

  \(p5_x\)：\(fa_x\) 无 cover 的概率。

设 \(f_x\) 表示 \(x\) 有 tag 的期望，\(g_x\) 表示 \(x\) 到根链上有 tag 的期望。经过一次 modify 后，\(f,g\) 的变化为：

\[f_x'\gets p_1+(p_2+p_5)f_x+p_4g_x\\ g_x'\gets (p_1+p_2)+(p_4+p_5)g_x \]

写成矩阵的形式：

\[\begin{bmatrix} f_x'&g_x'&1 \end{bmatrix} \gets \begin{bmatrix} f_x&g_x&1 \end{bmatrix} \times \begin{bmatrix} p_2+p_5&0&0\\ p_4&p_4+p_5&0\\ p_1&p_1+p_2&1 \end{bmatrix} \]

矩阵快速幂即可。

#include<bits/stdc++.h>
using namespace std;
const int N=4e5+5,mod=998244353;
int n,k,iv,tot,v1[N],v2[N],v3[N],ans;
struct mat{
	int x[3][3];
	friend mat operator*(mat a,mat b){
		mat c;
		for(int i=0;i<3;i++)
			for(int j=0;j<3;j++){
				c.x[i][j]=0;
				for(int k=0;k<3;k++) c.x[i][j]=(c.x[i][j]+1ll*a.x[i][k]*b.x[k][j])%mod;
			}
		return c;
	}
}x={0,0,1};
int qpow(int x,int n){
	int ans=1;
	for(;n;n>>=1,x=1ll*x*x%mod) if(n&1) ans=1ll*ans*x%mod;
	return ans;
}
mat qpow(mat x,int n){
	mat ans;
	for(int i=0;i<3;i++)
		for(int j=0;j<3;j++) ans.x[i][j]=i==j;
	for(;n;n>>=1,x=x*x) if(n&1) ans=ans*x;
	return ans;
}
int calc(int n){return 1ll*(1+n)*n/2%mod;}
void dfs(int p,int fa,int l,int r){
	v1[p]=1ll*l*(n-r+1)%mod*iv%mod;
	v3[p]=1ll*(calc(l-1)+calc(n-r))*iv%mod;
	v2[p]=(1-v1[p]-v3[p])%mod;
	int p1=(v1[p]-v1[fa])%mod,p2=v1[fa],p3=v2[p],
	p4=(v3[p]-v3[fa])%mod,p5=v3[fa],mid;
	ans=(ans+(x*qpow({(p2+p5)%mod,0,0,p4,(p4+p5)%mod,0,p1,(p1+p2)%mod,1},k)).x[0][0])%mod;
	if(l==r) return ;
	scanf("%d",&mid);
	dfs(++tot,p,l,mid),dfs(++tot,p,mid+1,r);	//注意广义线段树不能直接 p<<1,p<<1|1 分配编号
}
signed main(){
	scanf("%d%d",&n,&k),iv=qpow(calc(n),mod-2);
	dfs(tot=1,0,1,n),printf("%d\n",(ans+mod)%mod);
	return 0;
}