基于自适应Chirplet变换的雷达回波微多普勒特征提取

基于自适应Chirplet变换的雷达回波微多普勒特征提取

自适应Chirplet变换是一种强大的信号处理工具，特别适用于分析具有频率调制特性的非平稳信号，如雷达回波中的微多普勒效应。

1. 自适应Chirplet变换的基本原理

自适应Chirplet变换通过将信号分解为一系列Chirplet基函数，能够有效提取信号的时频特征。Chirplet是一种线性调频信号的片段，可以表示为：

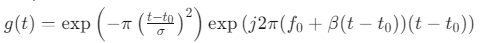
2. 微多普勒特征提取步骤

1. 信号预处理：对雷达回波信号进行预处理，如滤波、去噪等。
2. 自适应Chirplet分解：将雷达回波信号分解为多个Chirplet基函数，提取每个基函数的参数（时间中心、频率中心、调频率等）。
3. 特征提取：从分解后的Chirplet基函数中提取微多普勒特征，如频率变化率、幅度变化等。
4. 目标识别：利用提取的微多普勒特征进行目标识别，如通过Hough变换检测直线数量来判定群目标个数。

3. MATLAB实现

% 参数设置
fs = 1e6; % 采样率 1 MHz
c = 343; % 声速 343 m/s
t = 0:1/fs:1e-3; % 时间向量 1 ms

% 生成测试信号（假设目标具有微多普勒效应）
f0 = 1e3; % 初始频率 1 kHz
beta = 1e6; % 调频率 1 MHz/s
signal = exp(1j * 2 * pi * (f0 * t + 0.5 * beta * t.^2)); % 线性调频信号

% 自适应Chirplet变换
% 假设已知信号的初始频率和调频率，实际应用中需要通过优化算法估计这些参数
t0 = 0.5e-3; % 时间中心 0.5 ms
sigma = 0.2e-3; % 时间宽度 0.2 ms
chirplet = exp(-pi * ((t - t0) / sigma).^2) .* exp(1j * 2 * pi * (f0 + beta * (t - t0)) .* (t - t0));

% 计算Chirplet变换
C = abs(fftshift(fft(signal .* conj(chirplet))));

% 提取微多普勒特征
[~, idx] = max(C); % 找到最大值对应的频率索引
f_max = (-fs/2 + (idx - 1) * fs/length(C)) / 1e3; % 转换为kHz

% 显示结果
figure;
subplot(2, 1, 1);
plot(t, real(signal));
title('原始信号');
xlabel('时间 (s)');
ylabel('幅度');

subplot(2, 1, 2);
plot(linspace(-fs/2, fs/2, length(C))/1e3, C);
title('Chirplet变换');
xlabel('频率 (kHz)');
ylabel('幅度');

disp(['估计的微多普勒频率: ', num2str(f_max), ' kHz']);

参考代码 自适应Chirplet变换 用于分析提取雷达回波的微多普勒特征