基于L1范数约束的TV正则化算法求解目标函数

基于L1范数约束的TV正则化算法求解目标函数是一个在图像处理和机器学习中常见的问题，特别是在图像去噪、图像重建和特征选择等领域。

问题定义

目标函数通常定义为：

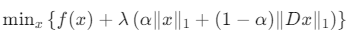
其中：

求解步骤

1. 初始化：选择初始解 ( x_0 ) 和设置算法参数（如迭代次数、步长等）。

2. 迭代更新：在每次迭代中，更新解 ( x ) 以最小化目标函数。这通常通过以下步骤完成：

   

3. 停止条件：检查是否满足停止条件，如最大迭代次数或目标函数的下降量小于某个阈值。

4. 输出：输出最终解 ( x )。

代码

以下是一个简单的 MATLAB 代码示例，用于求解基于L1范数约束的TV正则化问题。这个示例使用了 ADMM（Alternating Direction Method of Multipliers）算法。

function x = solveL1TV(A, b, lambda, alpha, maxIter)
    % 初始化
    x = zeros(size(A, 2), 1);
    z = zeros(size(A, 2), 1);
    u = zeros(size(A, 2), 1);
    D = diff(eye(size(A, 2)), 1, 1); % 差分矩阵
    rho = 1; % ADMM 参数

    for iter = 1:maxIter
        % x 更新
        x = (A' * A + rho * (I + D' * D)) \ (A' * b + rho * (z - u));

        % z 更新
        z = prox_l1(x + u, lambda * alpha / rho);

        % u 更新
        u = u + x - z;

        % 检查停止条件
        if norm(x - z) < 1e-4
            break;
        end
    end

    function y = prox_l1(x, tau)
        y = max(abs(x) - tau, 0) .* sign(x);
    end
end

基于L1范数约束的TV正则化算法求解目标函数

注意事项

• 选择合适的正则化参数 ( \lambda ) 和平衡参数 ( \alpha ) 对于算法的性能至关重要。
• ADMM 算法是一种有效的求解方法，但还有其他方法如梯度投影法、ISTA（Iterative Shrinkage-Thresholding Algorithm）等。
• 在实际应用中，可能需要对算法进行调整以适应特定的问题。

希望这个解释和示例对你有所帮助。如果你有任何进一步的问题或需要更详细的解释，请随时告诉我。