竞赛图性质之研究

定义

竞赛图是指由 \(n\) 个节点两两连一条有向边，共 \({n\choose 2}\) 条边组成的图。

性质

性质一：边性质

对于任意两个点 \(u,v\) 边 \((u,v)\) 与 \((v,u)\) 有且仅有一个存在。

证明：根据定义易得。

性质二：缩点链性质

竞赛图缩点后为一个无环竞赛图，拓扑序无重复，且拓扑序小的强连通分量里的所有点向拓扑序大的强连通分量里的所有点连边。

形象的来看，拓扑序构成一条“链”。

证明：

证明：

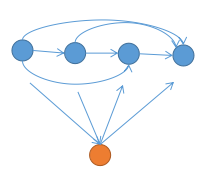
考虑归纳，逐强连通块加入。设目前有一条链，插入一个新连通块 \(x\)。

如果 \(x\) 连向所有点，放在链头；如果所有点连向 \(x\)，放在链尾。

否则 \(x\) 的出边一定都在 \(x\) 的入边的后边（否则成环）。

找到分界点，把 \(x\) 插在中间即可。

性质三：入度性质

在竞赛图中，如果 \(u\) 所在的强联通分量的拓扑序严格小于 \(v\) 的，则 \(in_u<in_v\)，其中 \(in_x\) 表示节点 \(x\) 的入度 。

证明：

设 \(u\) 所在的强联通分量为 \(t\)。考虑缩点后 \(1→t\) 的“链”，设链内包含的所有点构成集合 \(S\)。

由于不存在路径 \(v→u\)，所以 \(v∉S\)，且由于是竞赛图，于是 \(∀x∈S\)，存在 \(x→v\) 的有向边，于是 \(in_v≥|S|\)。

由于 \(S\) 外的点显然与 \(u\) 没有连边，而且 \(u∈S\)，于是 \(in_u<|S|≤in_v\)。

性质四：入度强连通确定性质

已知竞赛图所有点的 \(in\)，则可以确定每个强联通分量内包含的点。

证明：构造。考虑按照拓扑序便利所有的强连通分量，设遍历到的前若干个强联通分量里的所有点构成的集合为 \(S\)，则 \(\frac{|S|(|S|-1)}2=\sum_{x\in x}in_x\) 因为按拓扑序，后遍历的点一定不能与先遍历的点连边。

考虑把所有点按 \(in\) 升序排序成序列 \(a\)，由于结论 2 此时顺序遍历可以类比为拓扑序中顺序遍历。此时若 \(\frac {n(n-1)}2=\sum_{i=1}^nin_{a_i}\) 产生了一个新的强联通分量拓扑序遍历前缀。

考虑上一个满足条件的是 \(N'\)，初始 \(N'=0\)。则 \(S=\{a_x|x\in(N',N]\}\) 构成了一个新的强联通分量。由于拓扑序这样显然是不重不漏的。

性质五：通路性质

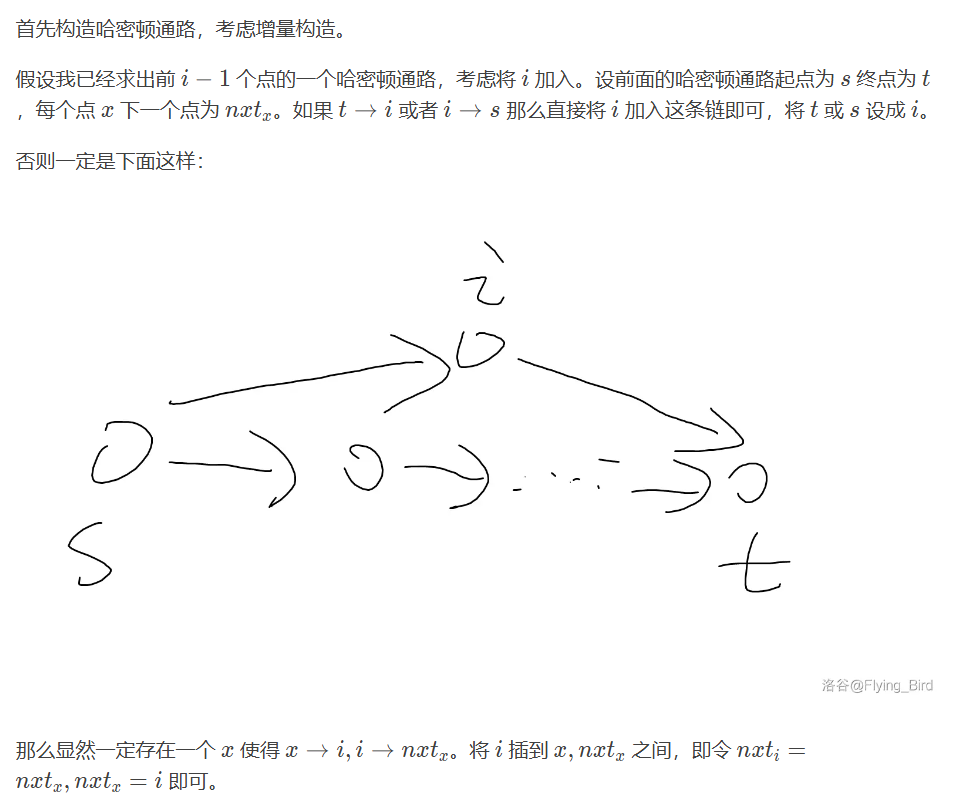
竞赛图一定有哈密顿通路

证明：构造证明

性质六：回路性质

强连通竞赛图一定有哈密顿回路

证明：构造证明

判定——兰道定理

定义

定义一个竞赛图的比分序列，是把竞赛图的每一个点的出度从小到大排列得到的序列。

定理内容

一个长度为 \(n\) 的序列 \(s=(s_1≤s_2,≤...≤s_n),n\ge 1\)，是合法的比分序列当且仅当：\(∀1≤k≤n,∑_{i=1}^k\limits s_i≥{k\choose 2}\)，且 \(k=n\) 时这个式子必须取等号。

证明

不会

例题

Tournament Construction

构造

参考

竞赛图性质研究(强联通分量/哈密顿回路) - HaHeHyt - 博客园 (cnblogs.com)

关于竞赛图 - 一粒夸克 - 博客园 (cnblogs.com)

竞赛图哈密顿路径 - 洛谷专栏 (luogu.com.cn)