关于竞赛图

竞赛图（有向完全图）

竞赛图也叫有向完全图。每对顶点之间都有一条边相连的有向图称为竞赛图。

竞赛图的一些简单的性质：

• 竞赛图没有自环，没有二元环；若竞赛图存在环，则一定存在三元环。（如果存在一个环大于三元，那么一定存在另一个三元的小环。）

• 任意竞赛图都有哈密顿路径（经过每个点一次的路径，不要求回到出发点）。

• 图存在哈密顿回路的充要条件是强联通。

• 哈密顿问题中，对于 n 阶竞赛图，当 n 大于等于 2 时一定存在哈密顿通路。

设 \(D\) 为 \(n\) 阶有向简单图，若 \(D\) 的基图为 \(n\) 阶无向完全图，则 \(D\) 为 \(n\) 阶竞赛图。

简单来说，竞赛图就是将完全无向图的无向边给定了方向。

一、兰道定理

兰道定理（\(\text{Landau’s Theorem}\)）是用来判定竞赛图的定理。

定义

定义一个竞赛图的比分序列(\(\text{score sequence}\))，是把竞赛图的每一个点的出度从小到大排列得到的序列。

定理内容

一个长度为 \(n\) 的序列 \(s=(s_1≤s_2,≤...≤s_n)\)，\(n≥1\)，是合法的比分序列当且仅当：

\[∀1≤k≤n,∑_{i=1}^k\limits s_i≥{k\choose 2} \]

且 \(k=n\) 时这个式子必须取等号。

定理证明

首先这个定理的必要性是显然的：即任一 \(n\) 阶竞赛图都满足这个条件。

现在我们只需要证明这个定理的充分性。

在这里，我们的证明是一个构造算法。思路是从一个一般竞赛图开始，每次改变两条边的方向，构造出一个比分序列是给定序列的竞赛图。

假设有一个一个满足定理条件的序列 \(s\)。现在我们构造一个及其平凡的 \(n\) 阶竞赛图 \(T_n\)，这个竞赛图的第 \(i\) 个节点向所有 \(j<i\) 的 \(j\) 节点都连有向边，因此其比分序列是 \((0,1,...,n−1)\)，我们要从这个平凡竞赛图开始构造。

考虑当前构造到了一个竞赛图 \(U\)，它的比分序列 \(u\) 满足：

\[∀1≤k≤n,∑_{i=1}^k\limits s_i≥∑_{i=1}^k\limits u_i \]

显然初始时 \(T_n\) 是满足这个条件的。

令 \(α\) 为第一个满足 \(s_α>u_α\) 的位置，这个位置显然存在不然就代表我们构造成功了。令 \(β\) 表示最后一个满足 \(u_α=u_β\) 的位置。

再考虑 \(γ\) 是第一个满足 \(s_γ<u_γ\) 的位置，这个位置肯定要严格大于 \(β\)，而且这个位置为什么一定存在呢？因为 \(∑^n_{i=1}\limits s_i=∑^k_{i=1}\limits u_i\) ，但是 \(β\) 及其以前的位置 \(s\) 都是要大于等于 \(u\) 的。

我们画一下这些位置大概是这样排列的

\[\begin{matrix} u_1 & u_2 & ... & u_\alpha &=& u_{\alpha+1} &=& ... &=& u_\beta&< & u_{\beta+1} & ... & u_{\gamma-1} &<& u_\gamma& ... &u_n\\ || & ||& ...& \land &&\land& & ... &&\land &&\land 或者|| &... &\land 或者|| &&\lor &...& ?\\ s_1 & s_2 & ... & s_\alpha & &s_{\alpha+1} && ...& & s_\beta && s_{\beta+1} & ... &s_{\gamma-1} && s_\gamma &... & s_n \end{matrix} \]

然后显然我们可以得到 \(u_γ>s_γ≥s_β>u_β\)，即 \(u_γ≥u_β+2\) 这个意味着什么呢？

考虑点 \(γ\) 和点 \(β\)， \(γ\) 的出度比 \(β\) 大 \(2\)，说明肯定至少有一个点 \(λ\) 满足 \(γ\) 向其连边而 \(β\) 没有向其连边（那么 \(λ\) 一定会向 \(β\) 连边），为什么要至少大 \(2\) 才满足呢？因为如果恰好大 \(1\) 的话多出来的这条边有可能是 \(γ\) 连向 \(β\)，这么 \(λ\) 这个点的存在性就不好说。

于是我们说明了至少存在一个 \(λ(λ≠β,λ≠γ)\) 满足存在有向边 \((γ,λ)\) 和 \((λ,β)\)。

考虑翻转这两条边，然后得到一个新的竞赛图，简单推导就可以发现它的比分序列 \(u′\) 一定仍然满足。

\[\forall 1\le k\le n,\sum_{i=1}^ks_i\ge\sum_{i=1}^ku'_i \]

且依然在 \(n=k\) 时一定取等号。

这样我们可以构造出一个新的竞赛图，可是为什么一直这样做就可以得到一个比分序列是 \(s\) 的竞赛图呢？

考虑定义两个竞赛图的曼哈顿距离

\[dist(u.s)=∑_{i=1}^n\limits |s_i−u_i| \]

显然，经过我的边翻转操作之后一定有 \(dist(u′,s)=dist(u,s)−2\)。并且任意时候由于 \(∑^n_{i=1}\limits s_i=∑^n_{i=1}\limits u_i\)，一定有 \(dist(u,s)≡0\pmod2\)（模 \(2\) 意义下可以拆开绝对值符号）。也就是说\(\dfrac{dist(u,s)}{2}\) 步我就可以构造出 \(s\) 序列所对应的竞赛图。

CF850D Tournament Construction

一个竞赛图的度数集合是由该竞赛图中每个点的出度所构成的集合。 现给定一个 \(m\) 个元素的集合，第 \(i\) 个元素是 \(a_i\) 。判断其是否是一个竞赛图的度数集合，如果是，找到点数最小的满足条件的竞赛图。

\(1\le m\le 31\) ， \(0\le a_i\le 300\) ，\(a_i\) 互不相同。

Solution

根据题意，原图最多有 \(30\times n\) 条边。而竞赛图的边数为 \(\dfrac {n(n-1)}2\) ，解得 \(n\le 61\) 。

根据兰道定理，我们将原 \(a\) 序列排序，并定义 \(f(i,j,y)\) 表示集合大小为 \(i\) ，构建出原图的点数为 \(j\) ，共有边数为 \(y\) 。

根据定理，则可知 \(y\geq \dfrac{j(j-1)}2\) 恒成立。

我们枚举 \(i,j,y\) ，并枚举 \(i-1\) 时的状态（例如有 \(k\) 个点，\(x\) 条边），若 \(f(i-1,k,x)\) 可行则 \(f(i,j,y)\) 可行。

顺便记录下此时的 \(j-k\) （即为有多少个点在出度集合中属于 \(i\) ）。

这样便能构造出原出度序列，然后根据兰道定理的证明构造即可。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[35],tmp[65],vis[65][35][4005];
int mp[65][65],s[65];
int main(){
	scanf("%d",&m);
	for(int i=1;i<=m;i++)scanf("%d",&a[i]);
	memset(vis,-1,sizeof(vis));sort(a+1,a+m+1);
	vis[0][0][0]=0;
	for(int i=0;i<=61;i++){
		for(int j=0;j<=m;j++){
			for(int t=i*(i-1)/2;t<=30*i;t++){
				if(vis[i][j][t]==-1)continue;
				if(j)vis[i+1][j][t+a[j]]=j;
				vis[i+1][j+1][t+a[j+1]]=j;
			}
		}
	}
	for(int i=m;i<=61;i++){
		if(~vis[i][m][i*(i-1)/2]){
			n=i;break;
		}
	}
	int lim=m,tot=n*(n-1)/2;
	for(int i=n;i;i--){
		tmp[i]=a[lim];
		tot-=a[lim];
		lim=vis[i][lim][tot+a[lim]];
	}
	for(int i=1;i<=n;i++){
		s[i]=i-1;
		for(int j=i+1;j<=n;j++)mp[j][i]=1;
	}
	while(1){
		int lim=0;
		for(int i=1;i<=n;i++){
			if(s[i]<tmp[i]&&s[i]!=s[i+1]){
				lim=i;break;
			}
		}
		if(!lim)break;
		int nxt=0;
		for(int i=lim+1;i<=n;i++){
			if(s[i]>tmp[i]){nxt=i;break;}
		}
		int top=0;
		for(int i=1;i<=n;i++){
			if(!mp[lim][i]&&mp[nxt][i]){
				top=i;break;
			}
		}
		mp[lim][top]^=1;mp[top][nxt]^=1;
		mp[top][lim]^=1;mp[nxt][top]^=1;
		s[lim]++;s[nxt]--;
	}
	printf("%d\n",n);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++)printf("%d",mp[i][j]);
		puts("");
	}


	return 0;
}

二、哈密顿路

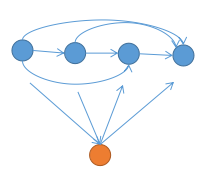
定理 1. 竞赛图强连通缩点后的DAG呈链状, 前面的所有点向后面的所有点连边

证明：

考虑归纳, 逐连通块加入，目前有一条链, 插入一个新连通块 \(x\) ，如果 \(x\) 连向所有点, 放在链头

如果所有点连向 \(x\), 放在链尾，否则 \(x\) 的出边一定都在 \(x\) 的入边的后边 (否则成环)

找到分界点, 把 \(x\) 插在中间即可。

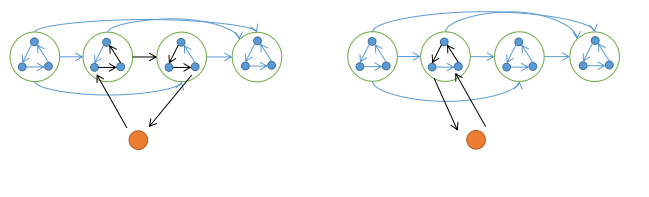
定理 2. 竞赛图的强连通块，存在一条哈密顿回路

证明：

考虑归纳, 逐点加入，目前有一条链, 链上的每个强连通块都存在哈密顿回路。

插入一个新点 \(x\), 只需证明新图中的强连通块都存在哈密顿回路即可。

如果不产生新连通块, 就是定理 \(1\) 中讨论的情况, 否则一定存在一条 \(x\) 的出边在 \(x\) 入边左边, 随便找一对。

如果是连到不同连通块, 见左图。

如果是同一连通块, 必定存在符合环的走向的相邻的一入一出, 见右图。

inline vector<int> solve(vector<int> vec){
	if(vec.size() == 1) return vec;
	vector<int> t;
	for(auto it:vec) t.insert(find_if(t.begin(), t.end(), [&](int x){return g[it][x];}), it);
	auto it = find_if(t.begin(), t.end(), [&](int x){return g[x][t[0]];}) + 1;
	vector<int> res(t.begin(), it);
	while(it != t.end()){
		auto r = it;
		while(find_if(res.begin(), res.end(), [&](int x){return g[*r][x];}) == res.end()) ++r;
		auto p = res.begin();
		while(p != res.end() && p + 1 != res.end() && !(g[*p][*it] && g[*r][*(p+1)])) ++p;
		res.insert(p == res.end() ? res.begin() : p + 1, it, r + 1); it = r + 1;
	}
	return res;
}

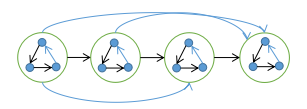
定理 3. 任意竞赛图都存在一条哈密顿路径

证明：

如图示方法构造：

for(int i = 1; i <= n; i++) if(!dfn[i]) tarjan(i);
for(int i = 1; i <= n; i++) Scc[scc[i]].push_back(i);
for(int i = 1; i <= tot; i++){
	Scc[i] = solve(Scc[i]);
	ans.insert(ans.end(), Scc[i].begin(), Scc[i].end());
}

[POI2017]Turysta

给出一个 \(n\) 个点的有向图，任意两个点之间有且仅一条有向边。

对于每个点 \(v\)，求出从 \(v\) 出发的一条经过点数最多，且没有重复经过同一个点两次及两次以上的简单路径。

Solution

\(\ge 3\) 个点的强连通竞赛图有哈密顿回路，因此从 \(u\) 开始最长的路径就是拓扑序在 \(u\) 所属的强连通分量之后 (包括其本身) 的强连通分量的哈密顿路径相连。在每个强连通分量找到哈密顿回路即可。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n;
int g[2005][2005];
int dfn[2005],low[2005],cnt,scc[2005],tot,stk[2005],top;
void tarjan(int x){
	dfn[x]=low[x]=++cnt;stk[++top]=x;
	for(int u=1;u<=n;u++){
		if(!g[x][u])continue;
		if(!dfn[u]){
			tarjan(u);low[x]=min(low[x],low[u]);
		}
		else if(!scc[u])low[x]=min(low[x],dfn[u]);
	}
	if(dfn[x]==low[x]){
		scc[x]=++tot;
		while(stk[top]!=x)scc[stk[top--]]=tot;
		top--;
	}
}
vector<int> Scc[2005],ans[2005];
inline vector<int> solve(vector<int> vec){
	if(vec.size()==1)return vec;
	vector<int> tmp;
	for(auto it:vec)tmp.insert(find_if(tmp.begin(),tmp.end(),[&](int x){return g[it][x];}),it);
	auto it=find_if(tmp.begin(),tmp.end(),[&](int x){return g[x][tmp[0]];})+1;
	vector<int> res(tmp.begin(),it);
	while(it!=tmp.end()){
		auto r=it;
		while(find_if(res.begin(),res.end(),[&](int x){return g[*r][x];})==res.end())++r;
		auto p=res.begin();
		while(p!=res.end()&&p+1!=res.end()&&!(g[*p][*it]&&g[*r][*(p+1)]))++p;
		res.insert(p==res.end()?res.begin():p+1,it,r+1);it=r+1;
	}
	return res;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		for(int j=1;j<i;j++){
			int x;scanf("%d",&x);
			if(x)g[j][i]=1;
			else g[i][j]=1;
		}
	}
	for(int i=1;i<=n;i++)if(!dfn[i])tarjan(i);
	for(int i=1;i<=n;i++)Scc[scc[i]].push_back(i);
	for(int i=1;i<=tot;i++){
		Scc[i]=solve(Scc[i]);
		for(auto x:Scc[i]){
			auto it=find_if(Scc[i].begin(),Scc[i].end(),[&](int u){return x==u;});
			ans[x].insert(ans[x].end(),it,Scc[i].end());
			ans[x].insert(ans[x].end(),Scc[i].begin(),it);
			for(int j=i-1;j;j--)ans[x].insert(ans[x].end(),Scc[j].begin(),Scc[j].end());
		}
	}
	for(int i=1;i<=n;i++){
		printf("%ld ",ans[i].size());
		for(auto it:ans[i])printf("%d ",it);
		puts("");
	}

	return 0;
}

P4233 射命丸文的笔记

从所有含有 \(n\) 个顶点（顶点互不相同）的，值得记录的竞赛图中等概率随机选取一个。

求选取的竞赛图中哈密顿回路数量的期望值。

Solution

首先算出不同的哈密顿回路的总数量，任意地选取一个环，方案数为 \((n-1)!\times 2^{\binom{n}{2}-n}\) ，即圆排列数乘边数。

设 \(g_i\) 表示有 \(i\) 个点的竞赛图的数量，\(g_i=2^{\binom{i}{2}}\) 。

设 \(f_i\) 表示有 \(i\) 个点的竞赛图强联通的方案数。

由于竞赛图缩点后会形成链状 \(\text{DAG}\)，枚举第一个连通块的大小来转移。

\[g_i=\sum_{j=1}^{i}\binom{i}{j}f_jg_{i-j} \\ g_i=\sum_{i=1}^{i}\frac{i!}{j!(i-j)!}f_jg_{i-j} \\ \frac{g_i}{i!}=\sum_{j=1}^{i}{\frac{f_j}{j!}\times\frac{g_{i-j}}{(i-j)!}} \]

设 \(F(x)=\sum_{i=1}^{n}{\frac{f_i}{i!}x^i}\) ，\(G(x)=\sum_{i=0}^{n}{\frac{g_i}{i!}}\) 。

\[G(x)=F(x)G(x)+1 \\ F(x)=1-\frac{1}{G(x)} \]

多项式求逆即可解决，时间复杂度为 \(O(n\log n)\) 。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int n;
const int md=998244353,G=3,Gi=(md+1)/3;
int r[1<<20];
inline int pwr(int x,int y){
	int res=1;
	while(y){
		if(y&1)res=1ll*res*x%md;
		x=1ll*x*x%md;y>>=1;
	}
	return res;
}
inline void NTT(int *dp,int lim,int W){
	for(int i=0;i<(1<<lim);i++)if(i<r[i])swap(dp[i],dp[r[i]]);
	for(int i=0;i<lim;i++){
		int w=pwr(W,(md-1)/(1<<(i+1)));
		for(int j=0;j<(1<<lim);j+=(1<<(i+1))){
			int Pw=1;
			for(int t=0;t<(1<<i);t++){
				int x=dp[j+t],y=1ll*Pw*dp[j+(1<<i)+t]%md;
				dp[j+t]=(x+y)%md;dp[j+(1<<i)+t]=(x-y+md)%md;Pw=1ll*Pw*w%md;
			}
		}
	}
}
int a[1<<20],b[1<<20],tmp[1<<20];
inline void mul(int *f,int *g,int N,int M){
	int lim=0;while((1<<lim)<=N+M)lim++;
	for(int i=0;i<(1<<lim);i++)r[i]=(r[i>>1]>>1)+((i&1)<<(lim-1));
	for(int i=0;i<N;i++)a[i]=f[i];
	for(int i=0;i<M;i++)b[i]=g[i];
	NTT(a,lim,G);NTT(b,lim,G);
	for(int i=0;i<(1<<lim);i++)tmp[i]=1ll*a[i]*(2-1ll*a[i]*b[i]%md+md)%md;
	for(int i=0;i<(1<<lim);i++)a[i]=0;
	for(int i=0;i<(1<<lim);i++)b[i]=0;
	NTT(tmp,lim,Gi);int inv=pwr(1<<lim,md-2);
	for(int i=0;i<(1<<lim);i++)tmp[i]=1ll*tmp[i]*inv%md;
}
void PolyInv(int *f,int *g,int lim){
	if(lim==1){
		f[0]=pwr(g[0],md-2);
		return ;
	}
	PolyInv(f,g,(lim+1)>>1);
	mul(f,g,lim,lim);
	for(int i=0;i<lim;i++)f[i]=tmp[i];
}
int f[1<<20],g[1<<20],inv[1<<20],fac[1<<20];
inline void init(){
	inv[0]=inv[1]=fac[0]=fac[1]=1;
	for(int i=2;i<=n;i++)fac[i]=1ll*fac[i-1]*i%md;
	for(int i=2;i<=n;i++)inv[i]=1ll*(md-md/i)*inv[md%i]%md;
	for(int i=2;i<=n;i++)inv[i]=1ll*inv[i]*inv[i-1]%md;
}
int main(){
	scanf("%d",&n);
	init();
	for(int i=0;i<=n;i++)g[i]=1ll*pwr(2,1ll*i*(i-1)/2%(md-1))*inv[i]%md;
	PolyInv(f,g,n+1);
	for(int i=0;i<=n;i++)f[i]=(md-f[i])%md;
	f[0]=(f[0]+1)%md;
	for(int i=0;i<=n;i++)f[i]=1ll*f[i]*fac[i]%md;
	if(n>=1)puts("1");
	if(n>=2)puts("-1");
	for(int i=3;i<=n;i++){
		int Pw=(1ll*i*(i-1)/2-i)%(md-1),w=1ll*fac[i-1]*pwr(2,Pw)%md;
		printf("%lld\n",1ll*w*pwr(f[i],md-2)%md);
	}


	return 0;
}