主流卡尔曼滤波推导——KF、EKF、IKF、UKF、ESKF

@

目录

• 一、高斯分布
  • 1.1 高斯概率密度函数
  • 1.2 联合高斯概率密度函数
  • 1.3 高斯随机变量的线性变换
• 二、滤波器基本原理
  • 2.1 贝叶斯滤波
• 三、卡尔曼滤波
  • 3.1 普通卡尔曼滤波器 (KF)
  • 3.2 扩展卡尔曼滤波(EKF)
  • 3.3 迭代扩展卡尔曼滤波(IEKF)
  • 3.4 无迹/无损卡尔曼滤波(UKF)
  • 3.5 误差状态卡尔曼(ESKF)
• 如果对您有帮助，就打赏一下吧O(∩_∩)O

论文资料：https://arxiv.org/pdf/2406.06427

一、高斯分布

1.1 高斯概率密度函数

一维情况下， 高斯概率密度函数表示为：

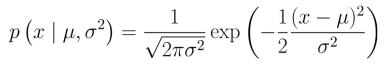
其中\(\mu\)为均值, \(\sigma^2\)为方差。
多维情况下， 高斯概率密度函数表示为

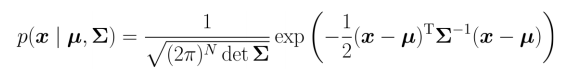
其中\(\mu\)为均值， 方差为\(\Sigma\) 。

1.2 联合高斯概率密度函数

1.3 高斯随机变量的线性变换

二、滤波器基本原理

符号说明：
\(\check{\boldsymbol{x}}\)是预测（先验）\(\hat{\boldsymbol{x}}\)校正值=观测值+预测值（后验）: \(\check{\boldsymbol{x}}_{k}=\boldsymbol{F}\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{v}_{k}\right)\)

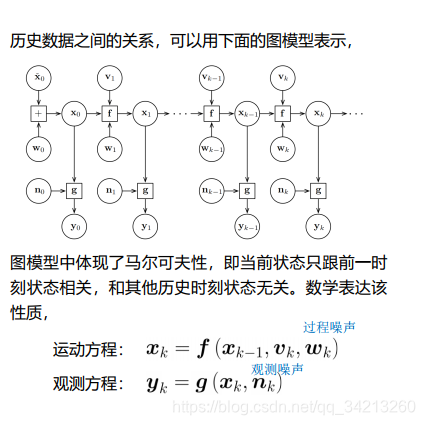
2.1 贝叶斯滤波

虚线表示可选,一般是没有的

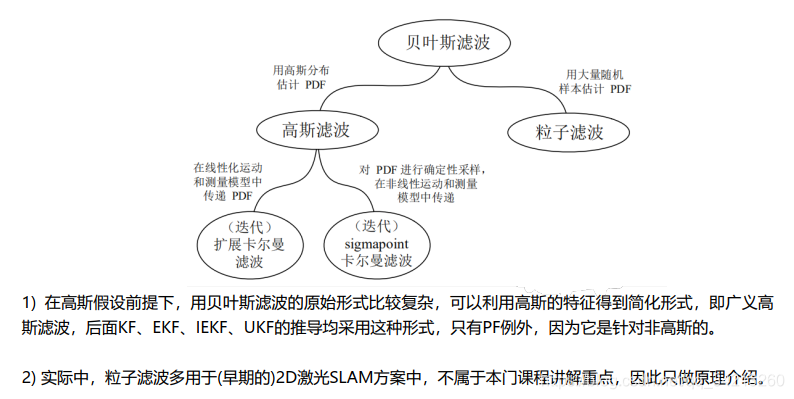
三、卡尔曼滤波

3.1 普通卡尔曼滤波器 (KF)

1.3 的推导得出的线性变换后的均值、 方差及交叉项带入上面的式子， 可以得到：

3.2 扩展卡尔曼滤波(EKF)

因为卡尔曼滤波的推导是建立在线性高斯假设的基础上的，因此当运动方程或观测方程为非线性的时候， 无法再利用之前所述的线性变化关系进行推导， 常用的解决方法是进行线性化， 把非线性方程一阶泰勒展开成线性。 即

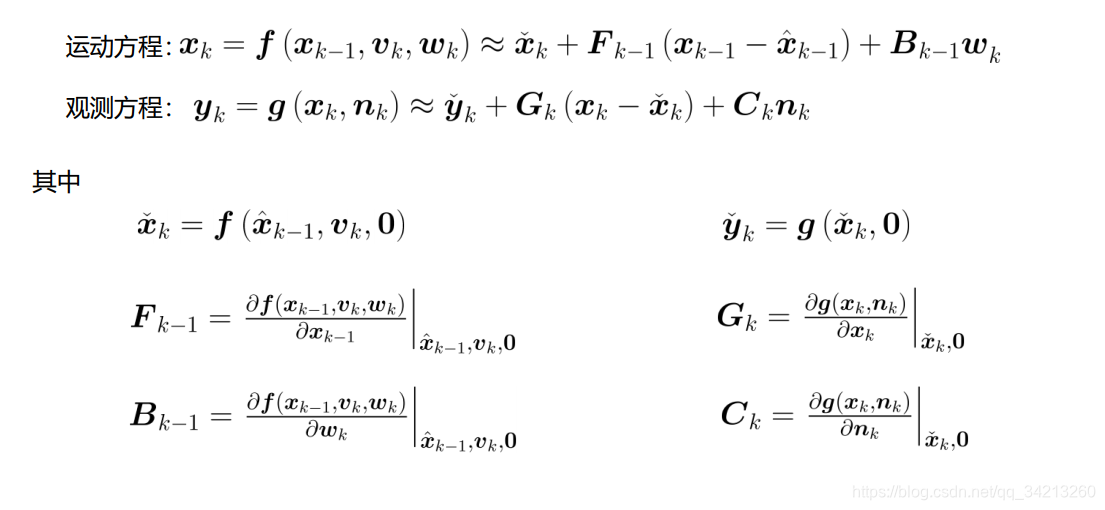
后面即可按照线性高斯下推导卡尔曼滤波的步骤进行推导， 最终得到经典五个公式

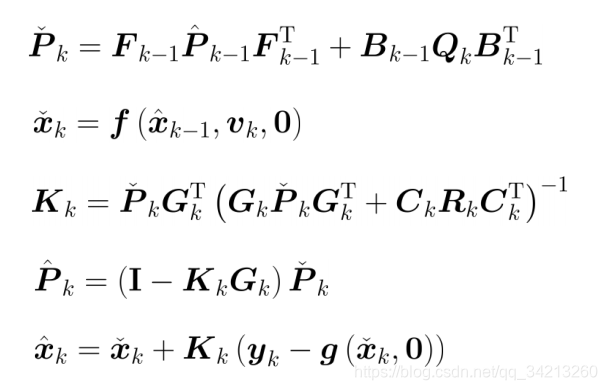
3.3 迭代扩展卡尔曼滤波(IEKF)

由于非线性模型中做了线性化近似， 当非线性程度越强时， 误差就会较大， 但是由于线性化的工作点离真值越近，线性化的误差就越小， 因此解决该问题的一个方法是， 通过迭代逐渐找到准确的线性化点， 从而提高精度。

在EKF的推导中， 其他保持不变， 仅改变观测的线性化工作点， 则有

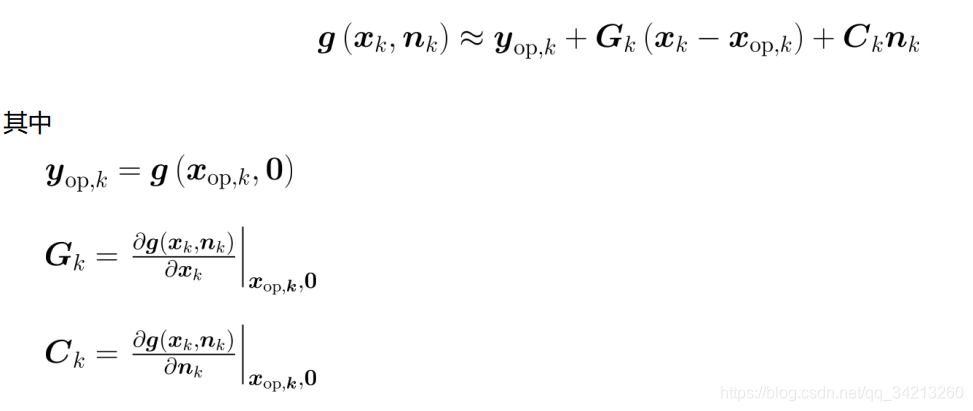
按照与之前同样的方式进行推导， 可得到滤波的校正过程为

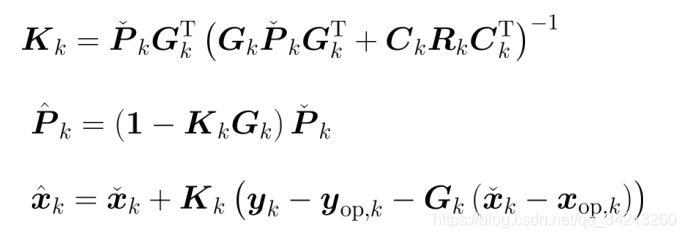
可见唯一的区别是后验均值\(\hat{x}_k\)更新的公式与之前有所不同。滤波过程中， 反复执行上面3个公式中的公式3， 以上次的后验均值作为本次的线性化工作点， 即可达到减小非线性误差的目的。

• 其中

\[ x_{op,k} = \hat{x}_k \\ y_{op,k} = g(x_{op,k},0) \]

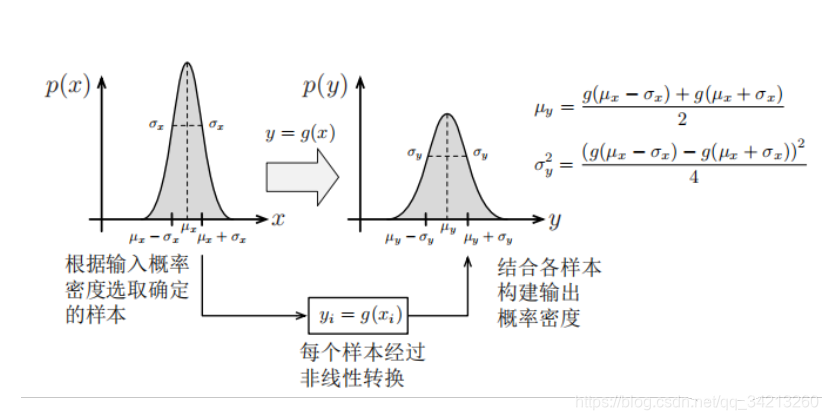
3.4 无迹/无损卡尔曼滤波(UKF)

该方法的核心思想是， 通过采样一部分sigmapoint点， 传入非线性函数， 通过计算这些点的分布， 来近似概率密度函数。

3.5 误差状态卡尔曼(ESKF)

状态量

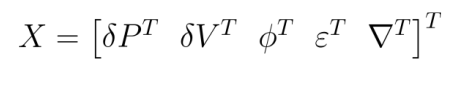
观测量：

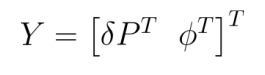
步骤 1：使用带误差的微分方程求出如下公式

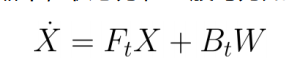
步骤2：状态方程为

步骤3：观察方程形式不变，变的只是含义·

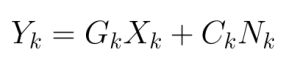
步骤4：卡尔曼5公式不变。与普通卡尔曼的区别仅仅是状态量和观测量从系统状态，变成了状态误差，从而导致F、G矩阵的改变。

如果对您有帮助，就打赏一下吧O(∩_∩)O

微信