海洋传播声场抛物方程解算方法-RAM详解
一、RAM模型概述
RAM(Range-dependent Acoustic Model)是基于抛物方程(PE)方法的海洋声场计算模型,专门用于处理距离相关(Range-dependent)的海洋环境(如声速剖面随距离变化、海底地形起伏、海面波动等)。其核心思想是通过抛物近似将三维声波动方程简化为二维(距离-深度)问题,结合步进Padé有理近似和能量守恒校正,实现高效的声场递推计算。
RAM模型的优势在于:
- 高效性:通过距离步进(Range-stepping)技术,避免了全波动方程的大规模矩阵求解,计算复杂度远低于有限元/边界元法;
- 灵活性:可处理复杂的海洋环境(如楔形海底、内波、海面起伏),支持多区域(Region)划分以适应参数渐变;
- 准确性:采用自启动器(Self-starter)构造初始场,能量守恒校正处理界面反射/透射,确保远场计算的稳定性。
二、RAM模型的核心算法原理
RAM模型的解算流程基于抛物方程的距离递推,核心步骤如下:
1. 抛物方程近似
从三维柱坐标系下的Helmholtz方程出发(忽略方位角耦合,适用于水平变化缓慢的环境):
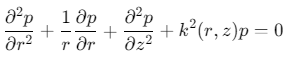
其中,\(p(r,z)\)为声压,\(r\)为水平距离,\(z\)为深度,\(k(r,z)=ω/c(r,z)\)为波数(\(ω\)为角频率,\(c(r,z)\)为声速)。
通过前向抛物近似(假设前向能量占主导,忽略后向散射),将椭圆型方程简化为抛物型初值问题:
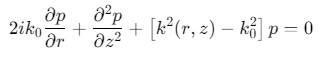
其中,\(k_0\)为参考波数(通常取声源中心频率对应的波数),\(∂p/∂r\)为距离方向的导数(前向传播)。
2. 步进Padé有理近似
为求解上述抛物方程,RAM采用n阶Padé有理近似对 exponential 函数(\(e^{ik0Δr}\))进行近似,将距离步进Δr内的声场更新分解为有理函数的和:
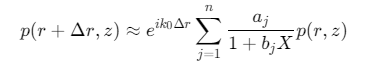
其中,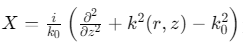 为横向算子(Depth operator),\(a_j\),\(b_j\)为Padé系数(通过多项式拟合确定)。
为横向算子(Depth operator),\(a_j\),\(b_j\)为Padé系数(通过多项式拟合确定)。
Padé近似的优势在于:比泰勒展开更高效(用低阶多项式近似高阶导数)、稳定性更好(避免指数增长导致的数值发散)。
3. 能量守恒校正
在距离相关环境(如海底地形突变、声速剖面骤变)中,界面处的能量通量需满足守恒条件(避免虚假反射或能量泄漏)。RAM通过复声压匹配实现界面校正:
-
对于水平界面(如海面/海底),强制声压p和法向质点振速vn连续:
![]()
其中,\(ρ\)为介质密度,下标1、2分别表示界面两侧介质。
-
对于倾斜界面(如海底斜坡),采用坐标变换(如沿界面法线方向重新网格化),将倾斜界面转化为水平界面处理。
4. 自启动器(Self-starter)
抛物方程的初值问题需要初始场(\(r=r_0\)处的声场),RAM采用自启动器构造准确的初始场:
-
对于点声源,初始场取简正波叠加(或通过解析解近似):
![]()
其中,\(ϕm(z)\)为第m阶简正波(Vertical mode),\(k_{rm}\)为水平波数,\(A_m\)为振幅(由声源强度决定)。
-
对于线声源,初始场取平面波近似(或通过傅里叶变换生成)。
三、RAM模型的MATLAB实现框架
RAM模型的官方实现是Fortran语言(如RAM 1.0/1.0p版本),但可通过MEX接口或MATLAB封装实现与MATLAB的集成。以下是MATLAB环境下的核心实现步骤:
1. 环境参数输入
首先定义海洋环境参数(声速剖面、海底地形、海面波动等),存储为结构化数组:
% 海洋环境参数结构体
env = struct();
env.freq = 50; % 声源频率 (Hz)
env.c = @(z) 1500 + 0.1*z; % 声速剖面 (m/s),随深度线性变化
env.rho = @(z) 1000 + 0.5*z; % 密度剖面 (kg/m³)
env.z_src = 100; % 声源深度 (m)
env.r_max = 10000; % 最大计算距离 (m)
env.dz = 10; % 深度方向网格步长 (m)
env.dr = 100; % 距离方向网格步长 (m)
2. 初始场构造(自启动器)
根据声源类型(点声源/线声源),生成初始场p(r0,z):
function p0 = self_starter(env)
% 点声源自启动器:简正波叠加
z = 0:env.dz:env.depth_max; % 深度网格
k0 = 2*pi*env.freq / env.c(0);% 参考波数
N_modes = 10; % 简正波数量
p0 = zeros(size(z));
for m = 1:N_modes
k_rm = k0 + 0.1*m; % 水平波数(近似)
phi_m = sin(m*pi*z/env.depth_max); % 简正波函数(示例)
A_m = 1 / norm(phi_m); % 振幅归一化
p0 = p0 + A_m * phi_m .* exp(1i*k_rm*env.dr); % 初始场叠加
end
end
3. 距离递推计算
采用Padé近似和能量守恒校正,实现声场的 distance-stepping 递推:
function p = ram_solver(env, p0)
% RAM模型距离递推求解
r = env.dr:env.dr:env.r_max; % 距离网格
z = 0:env.dz:env.depth_max; % 深度网格
N_r = length(r); % 距离步数
N_z = length(z); % 深度点数
p = zeros(N_r, N_z); % 声场矩阵
% 初始场赋值
p(1,:) = p0;
% Padé系数(示例:2阶Padé)
a = [0.5, 0.5];
b = [0.1, 0.2];
for ir = 2:N_r
r_prev = r(ir-1);
r_curr = r(ir);
delta_r = r_curr - r_prev;
% 计算横向算子X
k = 2*pi*env.freq ./ env.c(z); % 波数剖面
X = 1i/k0 * (diff(p(ir-1,:), 2)/env.dz^2 + (k.^2 - k0^2).*p(ir-1,:));
% Padé近似更新声场
p_curr = zeros(1, N_z);
for j = 1:length(a)
p_curr = p_curr + a(j)/(1 + b(j)*X) * p(ir-1,:);
end
% 能量守恒校正(界面处理)
if ir > 2 && env.interface_depth(r_curr) ~= env.interface_depth(r_prev)
p_curr = energy_conservation(p_curr, p(ir-1,:), env);
end
% 更新声场
p(ir,:) = p_curr .* exp(1i*k0*delta_r);
end
end
4. 能量守恒校正函数
处理界面处的能量通量连续:
function p_corr = energy_conservation(p_curr, p_prev, env)
% 界面深度(示例:海底斜坡)
z_interface = env.interface_depth(env.r(ir));
idx_interface = find(z >= z_interface, 1); % 界面索引
% 左侧(上层介质)和右侧(下层介质)的声压/振速
p_left = p_prev(1:idx_interface);
p_right = p_prev(idx_interface:end);
v_left = diff(p_left)/env.dz / env.rho(z(1:idx_interface));
v_right = diff(p_right)/env.dz / env.rho(z(idx_interface:end));
% 能量通量连续条件
E_left = sum(abs(p_left).^2 .* v_left);
E_right = sum(abs(p_right).^2 .* v_right);
scale_factor = sqrt(E_left / E_right); % 振幅缩放因子
% 校正声场
p_corr = p_curr;
p_corr(idx_interface:end) = p_curr(idx_interface:end) * scale_factor;
end
5. 结果可视化
计算完成后,通过MATLAB的绘图函数展示声场分布(如传播损失、声线轨迹):
% 传播损失计算(dB)
TL = -20*log10(abs(p(end,:)) / max(abs(p(end,:))));
% 绘制传播损失曲线
figure;
plot(TL, z);
xlabel('传播损失 (dB)');
ylabel('深度 (m)');
title('RAM模型计算结果:传播损失 vs 深度');
grid on;
四、RAM模型的优化与扩展
为提升RAM模型的计算效率和适应性,现有研究主要从以下方面进行优化:
1. 并行计算
RAM模型的距离递推是 embarrassingly parallel(任务间无依赖),可通过MPI(Message Passing Interface)实现并行计算(如1.0p版本的并行优化)。在MATLAB中,可使用parfor循环替代for循环,实现多核心并行:
parfor ir = 2:N_r
% 距离递推计算(同上)
end
2. 非均匀网格
在深度方向,对声速变化剧烈的区域(如温跃层、海底边界层)采用细网格,对变化缓慢的区域(如深海声道轴)采用粗网格,减少网格点数。例如:
% 非均匀深度网格生成
z = [0:env.dz_coarse:100, 100:env.dz_fine:500, 500:env.dz_coarse:env.depth_max];
3. 海面波动处理
对于起伏海面(如风浪),采用随机海面模型(如Pierson-Moskowitz谱)生成海面高度场zs(r),并将其纳入声速剖面计算:
% 随机海面生成(示例:高斯谱)
[z_s, k] = generate_random_sea(env.freq, env.wind_speed);
env.c = @(r,z) 1500 + 0.1*z + 0.01*z_s(r); % 声速剖面包含海面波动
参考代码 海洋传播声场抛物方程解算方法-RAM www.youwenfan.com/contentcnp/63676.html
五、RAM模型的应用场景
RAM模型广泛用于海洋声学工程,如:
-
声呐探测距离评估:计算不同海洋环境下的传播损失,预测声呐的作用距离;
-
水下通信链路预算:评估声波在起伏海面、海底地形下的传输损耗;
-
海洋环境噪声建模:结合噪声源(如船舶、海浪),计算水下噪声场的空间分布;
-
声学 tomography:通过声场反演海洋参数(如声速剖面、海流)。
六、总结
RAM模型是海洋声场抛物方程解算的经典方法,其核心是抛物近似+Padé递推+能量守恒。通过MATLAB的封装,可实现灵活的海洋环境模拟和声场计算。未来的发展方向包括:更高阶Padé近似(提升精度)、机器学习辅助优化(加速参数反演)、多物理场耦合(如声-流-固耦合)。

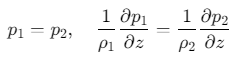
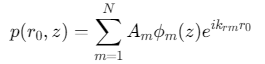

 浙公网安备 33010602011771号
浙公网安备 33010602011771号