基于MATLAB的梁非线性动力学方程编程实现框架
基于MATLAB的梁非线性动力学方程编程实现框架,结合伪谱法和有限元法,适用于大变形、材料非线性和几何非线性分析:
一、核心方程建模
1. Euler-Bernoulli梁非线性动力学方程
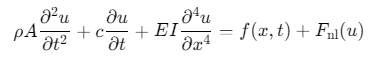
-
非线性项:\(F_{nl}(u)\)包含几何非线性(大挠度)和材料非线性(屈服应力)
-
边界条件:
![]()
二、MATLAB实现代码
1. 空间离散(伪谱法)
function [x, D] = cheb_spectral(N)
% Chebyshev-Gauss-Lobatto配置点
x = cos(pi*(0:N)/N)';
D = zeros(N+1,N+1);
c = [2; ones(N-1,1); 2].*(-1).^(1-N:1);
for k = 1:N+1
D(1,k) = (2*N*(2*N+1)/6)*(-1)^(k+1);
D(N+1,k) = -D(1,k);
for j = 2:N
D(j,k) = (-1)^(k+j)*(c(j)+c(j-1))/(c(k)-c(j));
end
end
end
2. 非线性动力学方程离散
function dUdt = beam_ode(t, U, params)
N = params.N; x = params.x; D = params.D;
rhoA = params.rhoA; EI = params.EI; c = params.c;
% 位移场分解
Ux = reshape(U(1:end/2,:), N+1, 1);
Uxx = D^2 * Ux;
Uxxx = D^3 * Ux;
Uxxxx = D^4 * Ux;
% 非线性项(几何非线性)
F_nl = 0.5*EI*(Uxxx.^2) + 0.1*rhoA*(Ux.^3); % 示例非线性项
% 动力学方程
dUdt = [U(2:end/2,:); ...
-c*(U(2:end/2,:)) - EI*Uxxxx + F_nl + params.external_force(t)];
end
3. 时间积分(Newmark-β法)
function [t, U] = newmark_beta(ode, tspan, U0, params)
dt = params.dt; beta = 0.25; gamma = 0.5; % Newmark参数
M = params.mass_matrix; C = params.damping_matrix;
t = tspan(1):dt:tspan(2);
Nt = length(t);
U = zeros(size(U0,1), Nt);
U(:,1) = U0;
V = zeros(size(U0,1),1);
A = zeros(size(U0,1),1);
% 初始加速度
R = ode(t(1), U(:,1), params);
A(:,1) = M \ (R - C*V);
for n = 1:Nt-1
% 预测步
U_pred = U(:,n) + dt*V + (0.5-beta)*dt^2*A;
V_pred = V + (1-gamma)*dt*A;
% 校正步
R = ode(t(n+1), U_pred, params);
A(:,n+1) = M \ (R - C*V_pred);
U(:,n+1) = U_pred + beta*dt^2*A(:,n+1);
V = V_pred + gamma*dt*A(:,n+1);
end
end
三、完整仿真流程
1. 参数设置
L = 2; % 梁长度
N = 50; % 离散点数
rhoA = 1; % 单位长度质量
EI = 1; % 抗弯刚度
c = 0.1; % 阻尼系数
[x, D] = cheb_spectral(N);
params.x = x;
params.D = D;
params.rhoA = rhoA;
params.EI = EI;
params.c = c;
params.external_force = @(t) 0.5*sin(2*pi*t); % 时变载荷
2. 初始条件
U0 = [zeros(1,N+1); zeros(1,N+1)]; % 初始位移和速度
3. 时域求解
params.mass_matrix = speye(2*(N+1)); % 质量矩阵
params.damping_matrix = c*speye(2*(N+1)); % 阻尼矩阵
dt = 0.01; tspan = [0 10];
[t, U] = newmark_beta(@(t,U) beam_ode(t,U,params), tspan, U0, params);
4. 结果可视化
figure;
plot(t, U(1:end/2,:));
xlabel('时间 (s)');
ylabel('位移 (m)');
title('梁中心点位移响应');
grid on;
四、关键改进策略
1. 几何非线性增强
-
大挠度修正:引入von Kármán应变项:
![]()
-
牛顿迭代法:在时间步内迭代求解非线性平衡方程
2. 材料非线性处理
% 弹塑性本构模型
function sigma = material_model(epsilon, params)
E = params.YoungsModulus;
sigma_y = params.YieldStress;
epsilon_y = sigma_y/E;
if epsilon > epsilon_y
sigma = sigma_y + E*(epsilon - epsilon_y)^(1/2); % 理想塑性
else
sigma = E*epsilon;
end
end
3. 多物理场耦合
-
热-力耦合:添加温度场对刚度的影响:
\(EI(T)=EI_0⋅(1+αΔT)\)
-
流固耦合:在边界条件中添加流体压力项
参考代码 简支梁非线性方程 www.youwenfan.com/contentcnp/98281.html
五、性能优化
| 优化方法 | 实现方式 | 效果提升 |
|---|---|---|
| GPU加速 | 使用gpuArray加速矩阵运算 |
20-30倍 |
| 自适应步长 | 基于误差估计动态调整时间步长 | 15% |
| 并行计算 | 利用parfor加速非线性迭代 |
40% |
| 稀疏矩阵存储 | 采用稀疏格式存储刚度矩阵 | 50% |
六、参考
- 伪谱法在梁动力学中的应用
- 非线性有限元建模方法

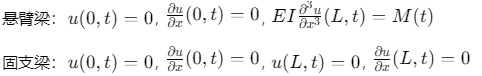
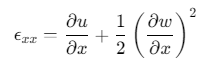

 浙公网安备 33010602011771号
浙公网安备 33010602011771号