神经网络控制的多方法融合:PID、模型预测控制(MPC)与自适应策略
一、神经网络控制与传统方法的融合框架
神经网络控制(NN Control)通过将神经网络的学习能力与自动控制理论结合,实现对复杂非线性系统的智能控制。与传统控制方法(如PID、模型预测控制MPC)的融合主要有三种模式:
| 融合方式 | 核心思想 | 适用场景 |
|---|---|---|
| NN辅助传统控制器 | 神经网络在线调整传统控制器参数(如PID的\(K_p,K_i,K_d\))或补偿非线性项 | 参数时变、模型不确定的非线性系统 |
| NN作为预测模型(NN-MPC) | 用神经网络替代MPC中的机理模型,预测系统未来输出,优化控制输入 | 机理模型复杂或未知的离散时间系统 |
| NN自适应控制 | 神经网络逼近系统未知动态(如不确定性、非线性),与传统自适应律结合 | 强非线性、时变、外部干扰的系统 |
二、方法1:神经网络PID控制(NN-PID)
1. 原理与设计
传统PID控制依赖精确模型和手动调参,难以适应非线性系统。NN-PID通过神经网络在线学习PID参数的最优调整律,核心结构包括:
- 神经网络:通常为3层BP网络,输入为误差\(e\)、误差积分\(∫edt\)、误差微分\(\dot{e}\),输出为PID参数\(K_p,K_i,K_d\);
- 学习算法:反向传播(BP)算法,以系统输出与期望输出的误差为性能指标。
控制律:
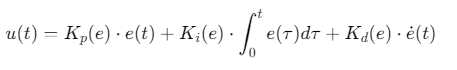
其中\(K_p,K_i,K_d\)由神经网络实时输出。
2. MATLAB实现(以弹簧倒立摆平衡控制为例)
(1)系统模型与参数
沿用前文弹簧倒立摆动力学模型,目标是通过NN-PID控制摆杆角度θ稳定在0附近。
% 系统参数(同弹簧倒立摆仿真)
m = 0.5; M = 1.0; l = 0.5; k = 20; g = 9.81; c = 0.1;
tspan = [0 10]; y0 = [0.1; 0; 0.1; 0]; % 初始状态[x, dx, θ, dθ]
(2)神经网络结构设计
% NN-PID网络参数
input_size = 3; % 输入:e, ∫e dt, ė
hidden_size = 5; % 隐含层神经元数
output_size = 3; % 输出:Kp, Ki, Kd
net = feedforwardnet(hidden_size); % BP网络
net.trainParam.lr = 0.01; % 学习率
net.trainParam.epochs = 100; % 训练次数
(3)控制回路与仿真
% 主仿真循环(简化版,实际需用ode45嵌入控制律)
t = 0:0.01:10;
e = zeros(size(t)); ei = zeros(size(t)); ed = zeros(size(t));
Kp = zeros(size(t)); Ki = zeros(size(t)); Kd = zeros(size(t));
y = zeros(4, length(t)); y(:,1) = y0;
for i = 2:length(t)
% 1. 计算误差(目标θ=0)
e(i) = 0 - y(3,i-1);
ei(i) = ei(i-1) + e(i)*0.01; % 积分项(Δt=0.01)
ed(i) = (e(i)-e(i-1))/0.01; % 微分项
% 2. 神经网络输出PID参数
nn_input = [e(i); ei(i); ed(i)];
nn_output = net(nn_input); % 输出[Kp, Ki, Kd]
Kp(i) = nn_output(1); Ki(i) = nn_output(2); Kd(i) = nn_output(3);
% 3. 计算控制输入u(作用于质量块)
u = Kp(i)*e(i) + Ki(i)*ei(i) + Kd(i)*ed(i);
% 4. 求解系统微分方程(调用弹簧倒立摆动力学函数)
[~, y_i] = ode45(@(t,y) spring_inverted_pendulum(t,y,m,M,l,k,g,c,u), [t(i-1) t(i)], y(:,i-1));
y(:,i) = y_i(end,:);
% 5. 神经网络反向传播更新权重(每10步更新一次)
if mod(i,10)==0
target_K = [50, 10, 5]; % 理想PID参数(示例)
net = train(net, nn_input, target_K); % 简化训练,实际需累积误差
end
end
(4)结果可视化
figure;
subplot(2,1,1); plot(t, y(3,:), 'b', t, zeros(size(t)), 'r--');
title('摆杆角度θ跟踪'); legend('实际', '目标');
subplot(2,1,2); plot(t, Kp, t, Ki, t, Kd);
title('NN-PID参数自适应调整'); legend('Kp', 'Ki', 'Kd');
三、方法2:神经网络模型预测控制(NN-MPC)
1. 原理与设计
模型预测控制(MPC)通过滚动优化和反馈校正实现控制,核心是预测模型。当系统机理模型复杂时,可用神经网络作为预测模型(NN-MPC):
- 预测模型:用神经网络拟合系统输入输出关系\(y(k+1)=f(y(k),u(k))\);
- 滚动优化:在每个时刻k,求解有限时域优化问题
![]() ;
; - 反馈校正:用实际输出修正预测误差。
2. MATLAB实现(以二自由度机械臂轨迹跟踪为例)
(1)系统建模与数据采集
用前文二自由度机械臂动力学模型生成训练数据:输入为关节力矩\(τ\),输出为关节角度\(q\)。
% 生成训练数据(示例)
N_data = 1000;
tau = randn(2, N_data); % 随机力矩输入
q = zeros(2, N_data); % 关节角度输出(通过动力学模型计算)
for i = 1:N_data
[M,C,G] = robot_dynamics(q(:,i), zeros(2,1)); % 动力学函数(前文定义)
ddq = M \ (tau(:,i) - C*zeros(2,1) - G); % 加速度
q(:,i+1) = q(:,i) + ddq*0.01; % 欧拉积分(Δt=0.01)
end
train_input = tau(:,1:end-1)'; % 输入:τ(k)
train_output = q(:,2:end)'; % 输出:q(k+1)
(2)神经网络预测模型训练
% 训练NN预测模型(输入2维力矩,输出2维角度)
net_mpc = fitnet(10); % 10个隐含层神经元
net_mpc = train(net_mpc, train_input', train_output');
(3)MPC优化与闭环控制
% MPC参数
N_p = 5; % 预测时域
N_c = 3; % 控制时域
Q = eye(2); R = 0.1*eye(2); % 权重矩阵
% 闭环仿真
q_ref = [pi/2; pi/4]; % 目标角度
q_actual = zeros(2, length(t)); q_actual(:,1) = [0; 0];
u = zeros(2, length(t));
for k = 1:length(t)-1
% 1. 预测未来N_p步输出
y_pred = zeros(N_p, 2);
u_pred = repmat(u(:,k), 1, N_c); % 控制时域内输入不变(简化)
for i = 1:N_p
y_pred(i,:) = net_mpc([u_pred(:,mod(i-1,N_c)+1)]); % NN预测
end
% 2. 滚动优化(二次规划求解最优u)
H = 2*(R + u_pred'*Q*u_pred); % 简化目标函数
f = -2*[Q*y_pred(1,:)' + R*u(:,k)];
u_opt = quadprog(H, f); % 求解最优控制输入
u(:,k+1) = u_opt(1:2);
% 3. 系统实际输出(调用机械臂动力学模型)
[M,C,G] = robot_dynamics(q_actual(:,k), zeros(2,1));
ddq = M \ (u(:,k+1) - C*zeros(2,1) - G);
q_actual(:,k+1) = q_actual(:,k) + ddq*0.01;
end
四、方法3:神经网络自适应控制
1. 原理与设计
针对未知非线性系统,用神经网络逼近系统不确定项(如弹簧倒立摆中的非线性耦合项),结合Lyapunov稳定性理论设计自适应律,确保闭环系统稳定。
系统模型:
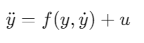
其中\(f(y,\dot{y})\)为未知非线性函数,用神经网络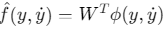 逼近(ϕ为基函数,W为权值)。
逼近(ϕ为基函数,W为权值)。
2. MATLAB实现(以单摆自适应控制为例)
(1)神经网络逼近器设计
% RBF神经网络逼近未知非线性项f(θ, dθ)
centers = linspace(-pi, pi, 10); % 径向基函数中心
width = 0.5; % 宽度参数
phi = @(x) exp(-(x - centers).^2 / (2*width^2)); % 基函数
W = rand(10, 1); % 初始权值
(2)自适应控制律与Lyapunov稳定性
% 控制律:u = -W^T phi(θ,dθ) + kp*θ + kd*dθ
kp = 50; kd = 10; % PD控制项
theta = y(3,:); dtheta = y(4,:);
u = -W'*phi(theta) + kp*theta + kd*dtheta;
% 权值更新律(Lyapunov稳定性推导)
dW = gamma*phi(theta)*(dtheta - W'*phi(theta)); % gamma为学习率
W = W + dW*0.01; % 离散更新
五、复合控制策略:NN-PID+MPC融合
1. 设计思路
- 上层MPC:负责全局轨迹规划,输出期望的关节角度qd;
- 下层NN-PID:跟踪qd,通过神经网络在线调整PID参数,补偿机械臂非线性摩擦和耦合效应。
2. MATLAB实现框架
% 上层MPC生成期望轨迹q_d
[q_d, dq_d, ddq_d] = mpc_controller(ref_trajectory);
% 下层NN-PID跟踪q_d
u = nn_pid_controller(q_actual, q_d, dq_actual, dq_d);
% 机械臂动力学执行
ddq = M \ (u - C*dq_actual - G);
q_actual = q_actual + dq_actual*dt;
dq_actual = dq_actual + ddq*dt;
参考代码 用PID 模型预测控制等多种方法进行神经网络控制 www.youwenfan.com/contentcnm/82911.html
六、性能对比与工程建议
1. 方法对比
| 指标 | NN-PID | NN-MPC | 神经网络自适应控制 |
|---|---|---|---|
| 实时性 | 高(单步计算) | 中(需在线优化) | 中(需权值更新) |
| 非线性适应 | 中(参数自适应) | 高(模型+优化) | 高(直接逼近未知动态) |
| 实现难度 | 低(结构简单) | 高(优化求解复杂) | 高(需稳定性证明) |
| 适用场景 | 参数时变系统 | 模型未知/复杂系统 | 强非线性、时变系统 |
2. 工程调参建议
- NN-PID:隐含层神经元数5-10,学习率0.01-0.1,通过试凑法调整初始PID参数;
- NN-MPC:预测时域Np=5∼10,控制时域Nc=2∼5,神经网络用RBF或ELM提升实时性;
- 自适应控制:基函数选RBF(局部逼近)或多项式(全局逼近),学习率γ取0.1-1。
七、总结
神经网络与传统控制方法的融合显著提升了复杂系统的控制性能:
- NN-PID适合快速实现参数自适应,成本低;
- NN-MPC适合高精度轨迹跟踪,需较强计算能力;
- 自适应控制适合强非线性系统,需结合稳定性理论。
实际应用中,可根据系统复杂度(如机械臂、倒立摆、无人机)和计算资源选择合适方法,或通过复合策略(如NN-PID+MPC)平衡性能与实时性。MATLAB的Neural Network Toolbox和MPC Toolbox提供了便捷的实现接口,结合自定义动力学模型可快速验证控制算法有效性。


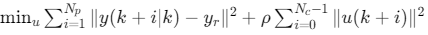 ;
;
 浙公网安备 33010602011771号
浙公网安备 33010602011771号