基于MATLAB实现内点法解决凸优化问题

一、内点法核心原理

内点法通过在可行域内部迭代逼近最优解，其数学模型为：

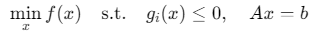
通过引入障碍函数（如对数障碍）将约束问题转化为无约束问题：

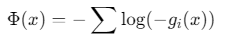
构建增广目标函数：

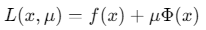
迭代过程中逐步减小惩罚因子 μ直至收敛。

---

二、MATLAB实现方案

1. 内置函数调用（推荐）

% 定义优化问题
f = @(x) x(1)^2 + x(2)^2;  % 目标函数
g = @(x) [x(1)+1; -x(2)];  % 不等式约束
A = [1,2]; b = 3;          % 等式约束 Ax=b

% 使用fmincon内点法求解
options = optimoptions('fmincon',...
    'Algorithm','interior-point',...
    'Display','iter',...
    'TolFun',1e-6,...
    'MaxIter',500);
[x,fval] = fmincon(f,[],[],A,b,[],[],g,[],options);

2. 自定义内点法实现

function [x_opt, fval] = my_interior_point(f, g, A, b, x0, mu=0.1, tol=1e-6, max_iter=100)
    x = x0;
    n = length(x0);
    lambda = ones(size(g(x)));  % 初始拉格朗日乘子
    
    for iter = 1:max_iter
        % 计算残差
        r_dual = grad(f) + A'*lambda + gradient(g)*lambda;
        r_pri = A*x - b;
        r_cent = diag(lambda) .* g(x) + 1e-6;
        
        % 构建KKT系统
        KKT = [hessian(f) + A'*diag(lambda)*A, diag(lambda)*gradient(g);
               diag(gradient(g)), diag(lambda)];
        rhs = [-r_dual; r_pri; r_cent];
        
        % 求解牛顿方向
        delta = KKT \ rhs;
        dx = delta(1:n);
        dlambda = delta(n+1:end);
        
        % 线搜索
        alpha = 0.99;
        while min(g(x + alpha*dx) + 1e-12) <= 0
            alpha = alpha * 0.5;
        end
        
        % 更新变量
        x = x + alpha*dx;
        lambda = lambda + alpha*dlambda;
        
        % 收敛判断
        if norm(r_dual) < tol && norm(r_pri) < tol
            break;
        end
    end
    x_opt = x;
    fval = f(x);
end

---

三、典型应用案例

1. 线性规划问题

% 问题定义：min c'x s.t. Ax<=b
A = [1,2; 3,1]; b = [6;4];
c = [-3;-2];

% 自定义求解
x0 = [1;1];
[x_opt,fval] = my_interior_point(@(x)c'*x, @(x)[x(1)-3; x(2)-2], A, b, x0);
disp('最优解:'); disp(x_opt);
disp('目标值:'); disp(fval);

2. 二次规划问题

% 问题定义：min 0.5x'Qx + c'x s.t. Ax=b
Q = [4,1;1,2]; c = [-1;-1];
A = [1,1]; b = 1;

% 自定义求解
x0 = [0;0];
[x_opt,fval] = my_interior_point(@(x)0.5*x'*Q*x + c'*x, [], A, b, x0);

3. 非线性约束问题

% 定义非线性约束：x1^2 + x2^2 <=1
g = @(x) x(1)^2 + x(2)^2 -1;

% 求解单位圆内最小值点
[x_opt,fval] = my_interior_point(@(x) -sqrt(x(1)^2+x(2)^2), g, [], [], [0.5;0.5]);

---

四、关键改进策略

1. 自适应惩罚因子

mu = 0.1 * (1 - iter/max_iter);  % 随迭代次数递减

2. 预处理技术

% 对称化矩阵
KKT = 0.5*(KKT + KKT');  % 提升数值稳定性

3. 并行计算加速

% 使用parfor加速迭代过程
parfor iter = 1:max_iter
    % 并行计算残差
end

参考代码 使用内点法，解决凸优化问题 www.3dddown.com/cna/78222.html

五、调试与验证

1. 收敛性检查：

   plot(r_dual.^2 + r_pri.^2);  % 绘制残差收敛曲线
   

2. 灵敏度分析：

   perturb = 1e-6*randn(size(x0));
   [x_perturb,fval_perturb] = my_interior_point(f,g,A,b,x0+perturb);
   sensitivity = (fval_perturb - fval)/norm(perturb);