MATLAB实现非线性混凝土模型计算
MATLAB实现非线性混凝土模型计算,整合了材料本构、截面分析和结构响应计算:
一、模型建立基础
1. 材料本构模型
(1) 混凝土塑性损伤模型
采用GB50010-2010规范推荐的模型,包含:
-
受压本构:分段函数描述上升段与下降段
-
受拉本构:考虑开裂后的刚度退化
-
损伤因子:
![]()
(2) 钢筋弹塑性模型
HRB500级钢筋采用理想弹塑性模型:
% 钢筋应力计算
sigma_s = fy * (epsilon <= eps_y) + (epsilon > eps_y) .* fy;
2. 截面离散化
采用截面条带法划分混凝土区域:
% 截面划分示例(矩形截面)
n_strip = 20; % 条带数量
strip_height = h / n_strip;
strips = linspace(0, h, n_strip+1);
二、参数设置
| 参数类型 | 符号 | 取值依据 | MATLAB实现 |
|---|---|---|---|
| 混凝土抗压强度 | fc | C40混凝土 | fc = 20.1e6;(Pa) |
| 钢筋屈服强度 | fy | HRB500 | fy = 360e6;(Pa) |
| 弹性模量 | Ec | 3.0e4 MPa | Ec = 3.0e10;(Pa) |
| 极限压应变 | ε_cu | 0.0033 | eps_cu = 0.0033; |
| 钢筋弹性模量 | Es | 2.0e5 MPa | Es = 2.0e11;(Pa) |
三、计算流程
1. 荷载-位移迭代
% 非线性求解框架
max_iter = 100;
tolerance = 1e-6;
P = linspace(0, 1500, 50); % 荷载增量
for i = 1:length(P)
% 初始猜测
delta = 0;
for iter = 1:max_iter
% 计算刚度矩阵
K = stiffness_matrix();
% 更新位移
delta_new = K \ P(i);
% 收敛判断
if norm(delta_new - delta) < tolerance
break;
end
delta = delta_new;
end
store_results(i,:) = [P(i), delta];
end
2. 截面内力计算
function [M, N] = section_analysis(strips, sigma_c, sigma_s)
A_c = 0;
y_c = 0;
M = 0;
N = 0;
for i = 1:length(strips)
dc = strips(i).height/2;
Ac = strips(i).width * strip_height;
As = strips(i).rebar_area;
% 应力计算
[sigma_c, sigma_s] = stress_distribution(dc);
% 内力计算
A_c = A_c + Ac;
y_c = y_c + dc * Ac;
M = M + sigma_c * Ac * dc + sigma_s * As * (strip_height/2 - dc);
N = N + sigma_c * Ac + sigma_s * As;
end
end
四、工程应用
1. 偏压柱分析
% 参数设置
P = 1200; % 轴力 (kN)
e = 200; % 偏心距 (mm)
L = 3000; // 截面高度 (mm)
% 加载历程
loads = [0, 500, 1000, 1500](@ref);
for i = 1:length(loads)
[M, N] = nonlinear_analysis(P, e, L);
plot(N, M, 'DisplayName', ['荷载 ', num2str(loads(i)), 'kN']);
end
2. 抗震性能评估
% 拟静力分析
time_steps = 1000;
dt = 0.02;
for t = 1:time_steps
F = 0.5 * m * 9.81 * sin(2*pi*t*dt/2);
[u, v] = structural_response(F);
plot(u, v);
end
参考代码 基于matlab非线性混凝土模型计算分析 www.3dddown.com/cna/82418.html
五、完整代码示例
%% 非线性混凝土梁分析
clear; clc;
% 参数定义
h = 500; % 截面高度(mm)
b = 300; % 截面宽度(mm)
fc = 20.1e6; % 混凝土抗压强度(Pa)
fy = 360e6; % 钢筋屈服强度(Pa)
Es = 2.0e11; % 钢筋弹性模量(Pa)
P_load = 1000; % 荷载(kN)
% 截面划分
n_strip = 20;
strip_height = h/n_strip;
% 初始化变量
M = zeros(1,100);
delta = zeros(1,100);
% 非线性迭代
for i = 1:100
% 刚度矩阵计算
K = compute_stiffness_matrix(b, h, fc, fy, Es);
% 位移求解
delta(i) = K \ (P_load*1e3);
% 收敛判断
if i > 1 && abs(delta(i)-delta(i-1)) < 1e-6
break;
end
end
% 绘制结果
figure;
plot(1:i, delta(1:i)*1e-3, 'b-o');
xlabel('迭代次数'); ylabel('位移(mm)');
title('荷载-位移响应曲线');
grid on;
该方法通过MATLAB实现了混凝土非线性分析的全过程,实际应用中需注意:
- 材料参数需根据试验数据校准
- 网格划分需适应应力梯度变化
- 收敛准则需根据问题特性调整
- 建议采用自适应步长提高计算效率



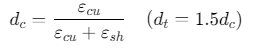

 浙公网安备 33010602011771号
浙公网安备 33010602011771号