线段树优化建图，前后缀优化建图

线段树优化建图求最短路

建图：

需要建两棵线段树，其中边朝上的称为入树，边朝下的称为出树。树中每条边的边权均为 \(0\)，仅表示可达性，并不会对最短路大小产生影响。

连边：

• 单点 \(u\) \(\rightarrow\) 区间 \([l, r]\)：入边中的单点连向出边中的 \(O(\log n)\) 个区间。
• 区间 \([l, r]\) \(\rightarrow\) 单点 \(u\) ：入边中的 \(O(\log n)\) 个区间连向出边中的单点。
• 区间 \([l_{1},r_{1}]\) \(\rightarrow\) 区间 \([l_{2},r_{2}]\)：建立虚点，入边中的 \(O(\log n)\) 个 \([l_{1},r_{1}]\) 连向虚点，虚点连向出边中的 \(O(\log n)\) 个 \([l_{2},r_{2}]\)。

这样相比于暴力连边，每次建边的复杂度从 \(O(n)\) 优化到了 \(O(\log n)\)。

求单源最短路，就是将入树中的源点作为起点，跑最短路，最终在出树的叶节点就代表了每个点的最短路。

例题：

CFdiv1 406 B

code

线段树优化建图上拓扑排序

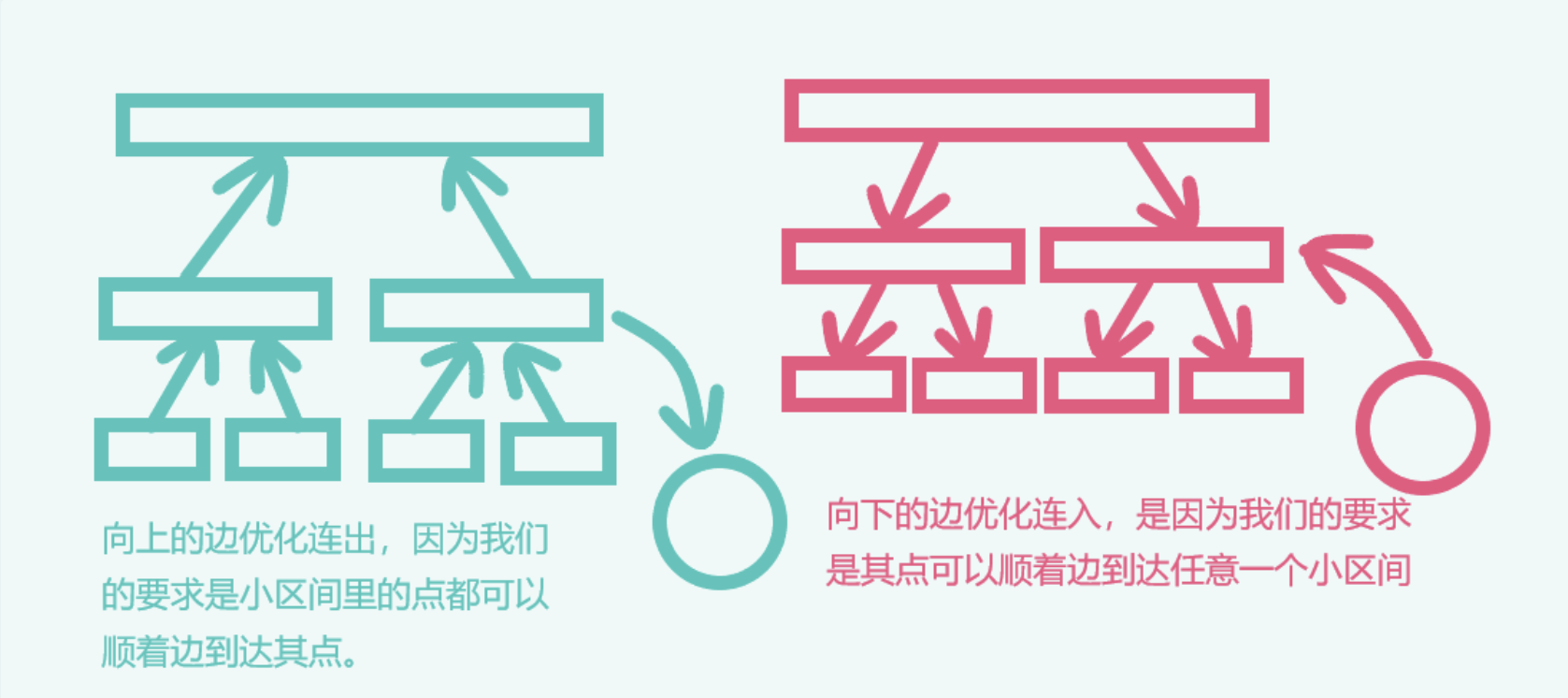
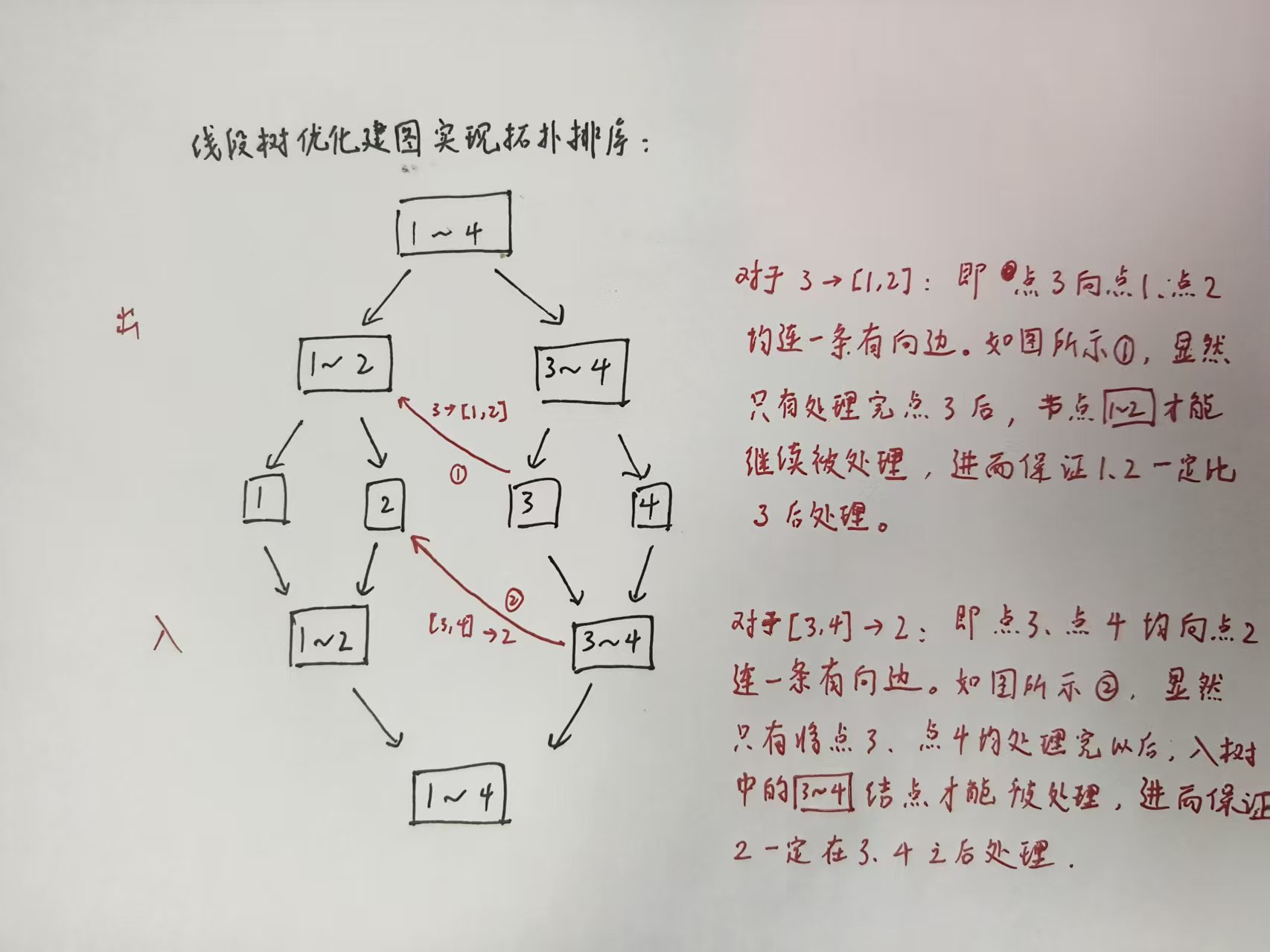
建图：线段树优化建图上拓扑排序需要将所有实际结点作为叶节点，并且每个叶节点是唯一的；同样是建两棵线段树，一棵出树一棵入树，只不过是共享叶节点。

原理见下图。

例题：

CFdiv2 914 F

tutorial

P13921
code

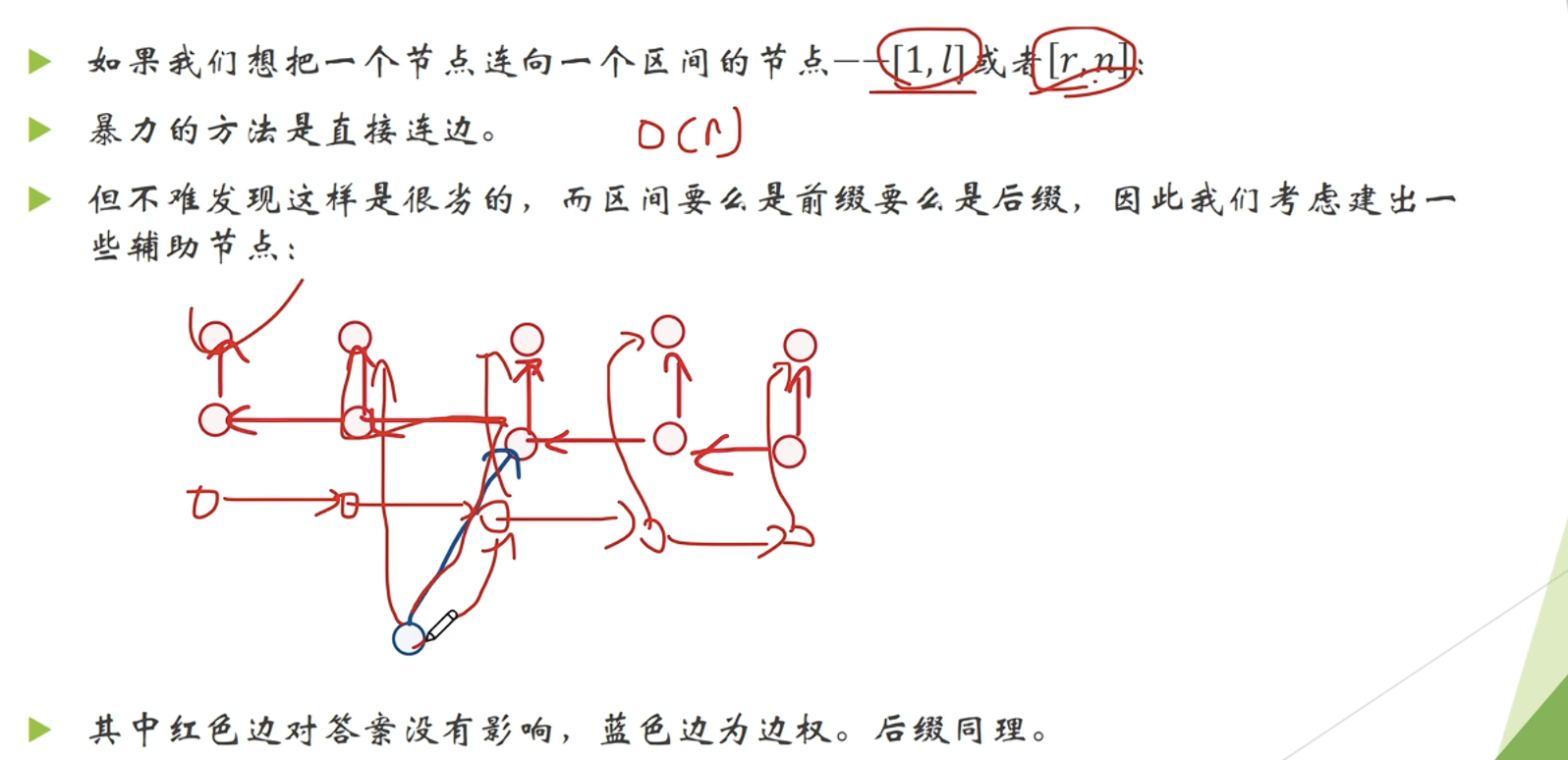
前后缀优化建图

经常用于处理完全图连边。

例题：

ABC232 G

在本题中，按照一些常规前后缀建图方式会出现边权为负的情况，而且前后缀建图的结构非常卡 spfa，因此需要利用一些性质以避免在建图中出现边权为负的情况。具体实现见代码。

code

CF 587D
code

P6965
code