为什么样本方差（sample variance）的分母是 n-1？
1. sample variance
今天看到一个很有趣的问题，也看到了两个不错的回答，感觉比较有趣，特此码住。
我们来简述一下问题：
如果已知随机变量 的期望为
，那么可以如下计算方差
：
上面的式子需要知道 的具体分布是什么（在现实应用中往往不知道准确分布），计算起来也比较复杂。
所以实践中常常采样之后，用下面这个 来近似
：
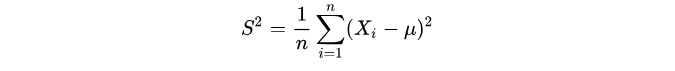
其实现实中，往往连 的期望
也不清楚，只知道样本的均值：
那么可以这么来计算 ：
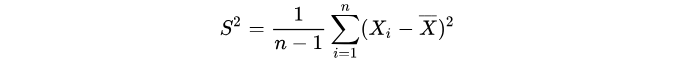
那这里就有两个问题：
- 为什么可以用
来近似
？
- 为什么使用
替代
之后，分母是
？
推导过程：
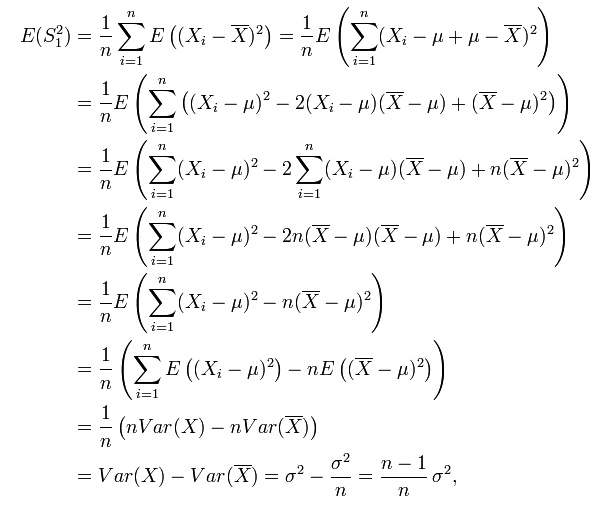
其实我对以上的推导过程的最后一步存在疑惑，即为什么：
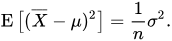
其实我在想，这个问题又回到了分母为什么是n-1的问题。
那我们就来考虑：
其实在这最后一步时：
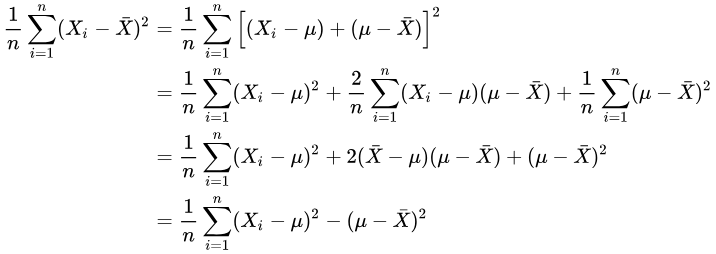
除非正好，否则我们一定有：
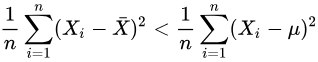
而不等式右边的那位才是的对方差的“正确”估计！
这个不等式说明了，为什么直接使用会导致对方差的低估。
那么，在不知道随机变量真实数学期望的前提下，如何“正确”的估计方差呢？答案是把上式中的分母换成
，通过这种方法把原来的偏小的估计“放大”一点点，我们就能获得对方差的正确估计了：
至于为什么分母是而不是
或者别的什么数，有机会要去看一下数学证明。
另外的理解是：自由度降低了1
样本方差与样本均值，都是随机变量，都有自己的分布，也都可能有自己的期望与方差。取分母n-1，可使样本方差的期望等于总体方差，即这种定义的样本方差是总体方差的无偏估计。 简单理解，因为算方差用到了均值，所以自由度就少了1，自然就是除以(n-1)了。
自由度降低：
我们来看一个例子
假设随机抽出的样本里只有两个数
如果这2个数是独立和随机抽取的，你就不能从x1猜出x2，例如我告诉你x1=10，请问x2等于多少？
你根本猜不出来，因为随机抽取让x2和x1之间没有关联。
但是，没想到的是，因为一个数据的存在，让这个随机取样产生了一个隐含的关联关系。
这个数就是计算样本方差 时，需要用到的样本平均值
，他的引入让随机抽取的独立性和自由度减少了一点点。
因为样本平均值 引入了一些信息，让x1和x2之间不再是相互独立的关系了。
根据平均值公式
只要知道了x1和，就可以计算出x2的值。
如果x1=10，=10，那x2=10
同样，知道了x2和，就可以计算出x1的值。
如果x2=10，=11，那x1=12
也就是说，出问题的并不是x1或者x2，这两个数本来好好的，互相独立的。出问题的是平均值，他引入的新信息，让样本数据之间的独立性减少了，关联性增加了。
或者还可以说，在平均值的介入下，x1和x2的自由度降低了，原来是两个独立的数，现在只有一个独立了，另一个则不再自由，好像有些人云亦云了。
同样的，对于更多的样本量：
如果样本是3个数
则知道了x1，x2，就能通过，计算出x3，独立性或者说自由度，就从3降到了2。
如果样本是4个数
则知道了x1，x2，x3，就能通过，计算出x4，独立性或者说自由度，就从4降到了3。
……
如果样本是n个数
则知道了x1，x2,..., ，就能通过
，计算出
，独立性或者说自由度，就从n降到了n-1。
平均值让样本的独立性或自由度减少了1，导致了样本出现了偏差。
这就是为什么样本方差的分母不是n，也不是n-2或n-3，而是n-1的原因。
参考链接：
https://www.cnblogs.com/yymn/p/4662447.html
https://www.matongxue.com/madocs/607.html
https://www.zhihu.com/question/20099757/answer/26586088
