KMP

不恋过往的全盘倾覆，只携前缀与后缀的默契共鸣，以预存的适配密码，在失配的岔路口轻转方向，奔赴下一场字符的重逢。—— 题记

Introduction

我们一定都听过字符串匹配问题：给定两个字符串 \(s\) 和 \(p\)（令 \(n = |s|, m = |p|\) ），求 \(p\) 在 \(s\) 中出现了几回，以及分别在何位置出现。

最朴素的想法是暴力的枚举每一个位置，判断是否匹配，时间复杂度 \(\mathcal O(nm)\)。

抑或是采用字符串哈希的算法，虽然时间为 \(\mathcal O(n + m)\)，但正确率却无法百分之百掌握。

由此引入这个算法：KMP 算法（ Knuth-Morris-Pratt 算法）。

由此可见，这个算法是由这三个人发明的。

花不哆嗦，进入正题。

KMP

那是一个阳光明媚的午后，你叫作 \(p\)，长度为 \(m\)。

你遇到了一个绝佳的女孩子，她是 \(s\)，长度为 \(n\)，你对她一见钟情，迫不及待地寻找着你和她身上的共同点。

失落——从头再来

你从每一个地方出发，逐一对比（见下图），就当你快要找到共同点时，却不可避免地发现了不同（标红部分），失望发现 \(p_i \ne s_j\)。

你无奈，你惋惜，却也无能为力，只待失配后的从头再来。

真的只能如此了吗？

不甘——汲取往昔

你不甘，你不服，学会吸取教训，想要微调后的胜利之路。

你尝试找到下一次匹配的最近的合法起点：

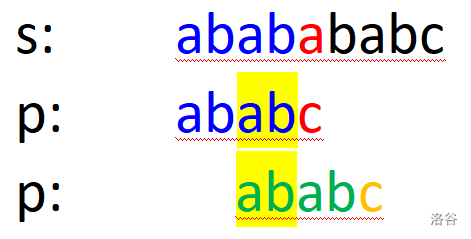
你回顾上次 \(p_1 ... p_{i - 1}\) 和 \(s_{j - i + 1} ... s_{j - 1}\) 的完美契合（蓝色部分），暗下决心找到下一个契机，让一个 \(k\) 满足 \(p_1 ... p_k\) 和 \(s_{j - k + 1} ... s_j\) 再次相同（第三行黄标部分）。

你惊讶地发现，那一段正好需要和你的 \(p_{i - k + 1} ... p_i\) 相匹配。

你惊讶地发现，此时你无需满足她的需要，只要有一个最大的 \(k < i\) 让自己的 \(p_1 ... p_k\) 和 \(p_{i - k + 1} ... p_i\) 共同就行。

你把这个 \(k\) 叫做你的将来，命名为 \(nxt_i\)，并将它作为第 \(i\) 次失败后的存档点。

它此时，就表示你的前 \(i\) 个字符，前后缀相等的最大匹配。

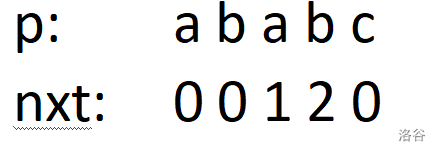
你的目标逐渐明晰，决心在每次失配时，轻调方向，回到 \(nxt_i\)，奔赴未来。

打击——自我成就

你庆幸，你开心，却忘却 \(nxt\) 的命。

你迷茫，你伤心，却又看到 \(nxt\) 生命的意义。

前缀与后缀的共鸣，这正是你自我匹配的目的。

成功——真理之光

你似在其中找到了真谛，自我匹配 KMP 维护的 \(nxt\) 让你豁然开朗。

int j = 0; // 你自我检索的指针
nxt[1] = 0;
for(int i = 2; i <= m; i ++){
	while(j && p[i] != p[j + 1]) j = nxt[j]; // 你退，携来时之路，直至适配之际，抑或无路可退
	if(p[i] == p[j + 1]) ++ j; // 你进，为去时之道，奠定成功之基，哪怕只能为 0
	nxt[i] = j;
}

终于，在又一个午后，你带着 \(nxt\) ，朝着她 \(s\)，走去。

丈量，轻退，重振雄风。

j = 0;
for(int i = 1; i <= n; i ++){
	while(j == m || (j && s[i] != p[j + 1])) j = nxt[j]; // 你学会了回到自身，与前后缀的默契共鸣，就算已成（j==m）也不怕退回再来
	if(s[i] == p[j + 1]) ++ j; // 你学会了走向前方，带着满满自信，继续匹配
	f[i] = j;
}

不再全盘推到，用自己成就自己，也许这才是 KMP 真正的勇气。

你发现，你的匹配指针最多只会向前 \(n + m\) 次，你也最多只会退 \(n + m\) 次。

在这 \(\mathcal O(n + m)\) 的时间里，你终于找到和她的共同之处。

向她表白，有情人终成眷属。

inline void KMP(){
	n = strlen(s + 1), m = strlen(p + 1);
	int j = 0;
	nxt[1] = 0;
	for(int i = 2; i <= m; i ++){
		while(j && p[i] != p[j + 1]) j = nxt[j];
		if(p[i] == p[j + 1]) ++ j;
		nxt[i] = j;
	}
	j = 0;
	for(int i = 1; i <= n; i ++){
		while(j == m || (j && s[i] != p[j + 1])) j = nxt[j];
		if(s[i] == p[j + 1]) ++ j;
		f[i] = j; // 最终的成果
	}
}

反思——未来新生

结婚后，你发现，你和她的适配度很高，你又想起来 KMP。

这次，你将你 \(p\) 和她 \(s\) 拼接起来，又在其中放一个字符做区分。

你发现，当时的算法在此刻，只需运行一次，你和她的相同，再度焕发生机。

你惊叹，你惋惜，你伤感，你高兴。

为自己匹配，也为他人匹配。

这也许也是 KMP 赠与你的勇气。

inline void KMP(){
	n = strlen(s + 1), m = strlen(p + 1);
	p[m + 1] = '+'; 
	for(int i = 1, j = m + 2; i <= n; j ++, i ++) p[j] = s[i]; // 你将自己与她连在一起，共同面对审查
	int j = 0, ans = 0;
	nxt[1] = 0;
	for(int i = 2; i <= m + n + 1; i ++){
		while(j && p[i] != p[j + 1]) j = nxt[j]; // 为自己，也为他人，退
		if(p[i] == p[j + 1]) ++ j; // 进
		nxt[i] = j;
	}
}

时光流转，当你在老年时，再次看着 KMP。曾经的 \(nxt\) 数组，可能已经不再适配于你。但他让你懂得：

不将过往匹配的痕迹尽数归零，而是以前缀与后缀的同源默契为基，用已证的契合成就新的衔接，让每一步过往都成为前行的阶梯，为着自己，也为他人。 —— 后记

后说

KMP 以 \(\mathcal O(n+m)\) 的高效复杂度，和百分百的正确率，完美地解决了许多刁钻的字符串问题。

许多题目，都可以最终转化成为 KMP 问题。

祝，不畏失败，以己为阶，再战未来。