【好题选讲】字符串基础算法好题选讲
前言
燃尽了,困死了。。。。
你可以先去看看:
P5446 [THUPC 2018] 绿绿和串串
考虑翻转操作一定会产生一个东西就是回文串。
发现这里保证 \(S\) 是最终的串 \(R\) 的前缀 的性质。我们从这里入手。
首先找到对于所有字符位置 \(i\),以这个字符为中心的最长回文串半径 \(p_i\)。注意这里考虑夹缝为中心的回文串(也就是长度为偶数的回文串)是没有意义的,因为题面中翻转操作的定义保证了翻转后来原串的末尾和新加的串的开头一定不会是相同字符,否则这两个字符将在反转操作中被合并。
先考虑最基本的情况:如果从这里开始的最长回文串触及了原串的末尾。
让我找找有没有图可以贺,哦终于有了,感谢写这份题解的同学!
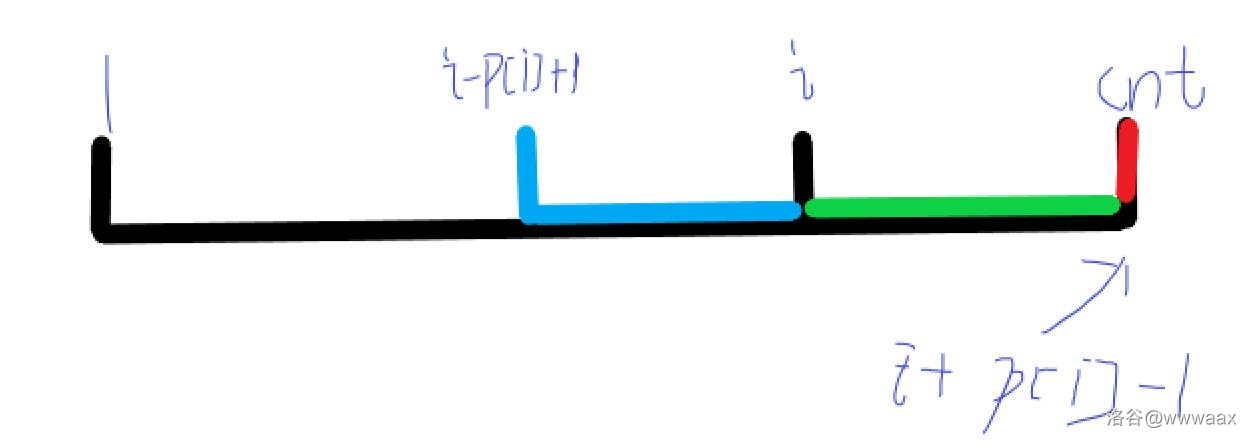
显然我们把 \(1\sim i-p_i+1\) 的串翻转拼接之后 \(1\sim cnt\) 就是这串的前缀,此时 \(i-p_i+1\) 是一个可能的答案。
那么只有 最长回文串触及了原串的末尾 可以贡献答案吗?当然不止,我们可以翻转很多次。
现在我们考虑翻转两次可以拼出 \(1\sim cnt\) 前缀的情况。
你会发现如果最长回文串既不触及原串的末尾,也不触及原串的开头,那这个东西是没用的,因为翻转操作至少要保证从开头到当前位置是要和后面相同的,而且这里也不是像最长回文串触及了原串的末尾一样只有一部分的情况。
所以我们只能考虑 最长回文串触及原串的开头的情况,此时从 \(1\sim i+p_i-1\) 就是 \(1\sim i\) 翻转拼接一次的结果,那么它可以在拼一次出现原串的前缀的条件是?
当然是 \(i+p_i\) 位置可以通过拼接一次出现原串的前缀。
于是,我们记录一个标记数组 \(ok_i=1\) 表示能在 \(i\) 位置通过拼接一次出现原串的前缀,考虑翻转两次时通过这个数组判断即可。
这样,考虑翻转更多次的情况,我们显然可以直接扩展这个数组的意义为 \(ok_i=1\) 表示能在 \(i\) 位置通过拼接 \(1\sim i\) 多次出现原串的前缀,这样就可以多次复用这个数组判断并记录答案了。
关于实现,求解最大回文半径的过程需要用 Manacher 算法,但是由于 Manacher 要在中间加入字符,所以当前位置在原串中的位置和最大回文半径都要除以二。
code
Show me the code
#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
int r[2200005];
string ms="^#";
int manacher(string s){
memset(r,0,sizeof r);
ms="^#";
for(int i=0;i<s.size();i++){
ms+=s[i];
ms+='#';
}
ms=ms+'$';
int cur=-1,ctr=-1;
int ans=0;
for(int i=0;i<ms.size();i++){
if(i<=cur){
r[i]=min(cur-i,r[2*ctr-i]);
}
else{
r[i]=1;
}
while (ms[i+r[i]+1]==ms[i-r[i]-1])r[i]++;
if(i+r[i]>cur){
ctr=i;
cur=i+r[i];
}
ans=max(r[i],ans);
}
return ms.size();
}
bool ok[2000006];
int main(){
int n;cin>>n;
while(n--){
memset(ok,0,sizeof ok);
string s;cin>>s;
int rl=s.size();
if(rl==1){cout<<1<<'\n';continue;}
int len=manacher(s);
set<int> ans;
for(int i=len;i>=1;i--){
int rev=r[i]/2;
int cl=i/2;
if(ms[i]<'a'||ms[i]>'z')continue;
if(cl+rev==rl){ans.insert(cl);ok[cl]=1;}
else if(cl-rev==1&&ok[cl+rev]){ans.insert(cl);ok[cl]=1;}
}
for(int v:ans)cout<<v<<' ';
cout<<'\n';
}
return 0;
}
P2375 [NOI2014] 动物园
这题有用 KMP Border 理论的 \(O(nL)\) 优秀算法,但是我还有一个用 Zfunc 的 \(O(nL)\) 算法。
首先对原串算出它的 Zfunc。
考虑每个 \(z_i\),你会发现既是它的后缀又是它的前缀还不能重叠这样的串在 \(i\) 位置就是 \(s[1,1]\) 和 \(s[i,i]\),\(i+1\) 就是 \(s[1,2]\) 和 \(s[i,i+1]\)。也就是这个东西会贡献给 \(i\) 及其之后的一些位置一个串的答案。
考虑这个位置是什么,如果 \(i\notin[1,z_i]\),那么显然 \([i,i+z_i-1]\) 的位置都是可以贡献到的,因为这些前缀后缀一定不会重叠。
但是如果 \(i\in[1,z_i]\),那么就只能贡献到 \([i,i+(i-1)-1]\) 的位置了,因为 \([1,i]\) 和 \([i,i+z_i-1]\) 是有重合的,这样在此及其后的所有串都是不合法的,无法被贡献。
于是问题变成了一堆区间加和一次全局求和,这个东西差分数组就可以。时间复杂度是 \(O(nL)\)。
下面的 code 用了树状数组,我也不知道我当时为什么要写树状数组。
Show me the code
#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e6+6;
const int mod=1e9+7;
int nxt[N],z[N];
int c[N];
int m;
void add(int p,int k){for(;p<=m;p+=(p&(-p)))c[p]+=k;}
ll pf(int r){
ll sum=0;
for(;r>0;r-=(r&(-r))){sum+=c[r];}
return sum;
}
int main(){
int n;cin>>n;
while(n--){
string s;cin>>s;
m=s.size();
memset(nxt,0,sizeof nxt);
memset(z,0,sizeof z);
memset(c,0,sizeof c);
for(int i=1,l=0,r=0;i<m;i++){
if(i<=r&&z[i-l]<r-i+1)z[i]=z[i-l];
else{
z[i]=max(0,r-i+1);
while(i+z[i]<m&&s[z[i]]==s[i+z[i]])z[i]++;
}
if(r<i+z[i]-1)l=i,r=i+z[i]-1;
}
ll ans=1;
for(int i=1;i<=m;i++){
int lbc=min(i-1,z[i-1]);
add(i,1);add(i+lbc,-1);
}
for(int i=1;i<=m;i++)ans=ans*(pf(i)+1)%mod;
cout<<ans<<'\n';
}
return 0;
}
P4555 [国家集训队] 最长双回文串
这题好像很水啊,我们首先一遍 Manacher 跑出以所有字符或者夹缝中间开始的最长回文串。
然后记录每个点开始向右扩展能扩展出来的最长的回文串,这个由我们 Manacher 出来的数组给左右端点算贡献即可。
接下来再次枚举 Manacher 来的回文的右端点,加上右端点加一位置能扩展出来的最长的回文串长度,统计答案即可。
这个题为下文做铺垫,吸引读者阅读兴趣。
xde:表现手法都有哪些?
code
Show me the code
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=2e5+5;
int r[N];
int lft[N],rgt[N];
string ms="^#";
void manacher(string s){
memset(r,0,sizeof r);
for(int i=0;i<s.size();i++){
ms+=s[i];
ms+='#';
}
ms=ms+'$';
// cout<<ms<<'\n';
int cur=-1,ctr=-1;
int ans=0;
for(int i=0;i<ms.size();i++){
if(i<=cur){
r[i]=min(cur-i,r[2*ctr-i]);
}
else{
r[i]=0;
}
while (ms[i+r[i]+1]==ms[i-r[i]-1]){
r[i]++;
lft[i+r[i]]=max(lft[i+r[i]],r[i]);
rgt[i-r[i]]=max(rgt[i-r[i]],r[i]);
}
if(i+r[i]>cur){
ctr=i;
cur=i+r[i];
}
lft[i+r[i]]=max(lft[i+r[i]],r[i]);
rgt[i-r[i]]=max(rgt[i-r[i]],r[i]);
}
}
int main(){
string s;
cin>>s;
manacher(s);
int ans=0;
for(int i=2;i<ms.size()-2;i++){
// cout<<ms[i]<<' ';
if(ms[i]=='#'){
ans=max(ans,max(lft[i]+rgt[i+1],lft[i]+rgt[i]));
}
else ans=max(ans,lft[i]+rgt[i+1]);
}
cout<<ans;
return 0;
}
P3546 [POI 2012] PRE-Prefixuffix
什么 Border 不 Border 的,让我们来想点好玩的东西!
首先题面的意思是让你求出三个原串的子串 \(A,B,C\),且原串可以表示成这样的形式:
要求 \(AB\) 最长长度且 \(C\) 不为空串。
此时我们把原串这样处理:
然后你会发现字符串变成了 \(AABBC\) 的形式。于是现在题目变成了上面那个题。但是要求这两个串的左端点必须是 \(1\) 而已。
感觉很莫名其妙对吗(
code
Show me the code
P5829 【模板】失配树
以后可能会把这东西重构进 KMP 里面去,先存个档吧。
不知道你有没有发现 KMP nxt 数组一个特点:\(nxt[i]<i\)。
然后数次被题面坑惨的经历告诉我们,如果我们把所有 \(i\) 变成点,nxt 表示连边,那么我们会得到一棵树。
于是你跳 nxt 的过程就可以变成在树上往祖先跳的过程,同时,我们还可以知道从各位置出发的 Border 之间的联系。
我们把这个树叫做 fail 树,也叫失配树。
树这东西可太带派了,一些东西放在树上就会很好做,比如这题的最长公共 Border。
当然是两个位置在 fail 树上的 LCA 了!
其实不是的,因为 Border 不能等于自己,于是我们找到两点之间的 LCA 之后,还要再跳一次 father。
code
Show me the code
#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e6+6;
const int lgr=26;
int nxt[N];
vector<int> edge[N];
int dep[N];int fa[N][30];
void bfs(int s){
memset(dep,0x3f,sizeof dep);
dep[0]=0;dep[s]=1;
fa[0][0]=0;fa[s][0]=0;
queue<int> q;q.push(s);
while(q.size()){
int u=q.front();q.pop();
for(int v:edge[u]){
if(dep[v]>dep[u]+1){
dep[v]=dep[u]+1;
q.push(v);
fa[v][0]=u;
for(int i=1;i<=lgr;i++)fa[v][i]=fa[fa[v][i-1]][i-1];
}
}
}
return ;
}
int lca(int u,int v){
if(u==v)return fa[u][0];
if(dep[v]>dep[u])swap(u,v);
for(int i=lgr;i>=0;i--){
if(dep[fa[u][i]]>=dep[v]){u=fa[u][i];}
}
if(u==v)return fa[u][0];
for(int i=lgr;i>=0;i--){
if(fa[u][i]!=fa[v][i]){
u=fa[u][i];v=fa[v][i];
}
}
return fa[u][0];
}
int main(){
string b;cin>>b;
int m=b.size();b=' '+b;
nxt[1]=0;
edge[1].push_back(0);edge[0].push_back(1);
for(int i=2,j=0;i<=m;i++){
while(j&&b[i]!=b[j+1])j=nxt[j];
if(b[i]==b[j+1])j++;
nxt[i]=j;
edge[i].push_back(j);
edge[j].push_back(i);
//cout<<"llvm: "<<i<<' '<<j<<'\n';
}
bfs(0);
int q;cin>>q;
for(int i=1;i<=q;i++){
int u,v;u=rd;v=rd;
cout<<max(0,lca(u,v))<<'\n';
}
return 0;
}
P3435 [POI 2006] OKR-Periods of Words
说说传统的 KMP 做法和我胡出来的 Z func 做法。下面我我们让 \(S\) 的下标从 \(1\) 开始。
考虑 Border 的本质,不严谨的描述为:
则称 \(A\) 是 \(S\) 的一个 Border。
那么你会发现,对于 \(S\) 串,它的一个真前缀就是 \(AB\),它的最长真前缀就是要找到 \(S\) 的最小 Border \(T\),此时的 \(TB\) 一定是最长的。
还记得上面我们讲了什么嘛,失配树就可以求出每个位置出发的最小 Border。
就是从每个点找到最浅的非根节点和自己的点,(根节点是 \(0\) 号点代表没有 Border。)这个点的编号就是最小 Border 的长度和在原串中的位置。
用倍增在 fail 树上找这个是容易的,时间复杂度 \(O(n\log n)\)。
但是我写的是 Zfunc + 线段树做法,翻了圈题解好像没这个做法?
从这里我们让 \(S\) 的下标从 \(0\) 开始。
首先求出所有位置的 Zfunc \(z_i\),然后还是分类讨论 LCP 相交的情况。
如果 \(0\sim z_i-1\) 与 \(i\sim i+z_i-1\) 不相交,此时你会发现 \(0\sim i-1\) 就是所有 \(i\sim i+z_i-1\) 位置的一个可能的真前缀,长度为 \(i\),对 \(i\sim i+z_i-1\) 位置区间覆盖记录最大值。
如果 \(0\sim z_i-1\) 与 \(i\sim i+z_i-1\) 相交,考虑求出相交区间的长度 \(dt=(z_i-1)-i+1\)。
然后对于 \(i \sim i+z_i-dt-1\) 这段的真前缀为 \(0\sim z_i-dt-1\),长度为 \(z_i-dt\),区间覆盖记录最大值。
对于尾巴上长度为 \(dt\) 的那一段,由 Zfunc 的性质容易知道它与主串开头 \(0\sim dt\) 的那一段一定是相等的。
于是这一小段的真前缀就是 \(0\sim i+z_i-dt-2\),长度为 \(i+z_i-dt-1\),对区间 \(i+z_i-dt\sim i+z_i-1\) 间覆盖记录最大值。
不是这东西我是怎么推出来的。。。总之还是画画图就懂了。
区间覆盖记录最大值部分胡上个线段树即可。
但是喜提最劣解,别的 AC 记录都只跑 \(100\)ms,但是我快跑了 \(1\)s。。
code
Show me the code
#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
const int N=1e6+5;
int z[N];
int ans[N];
struct seg{
int l,r;
int maxv;
}t[N<<2];
void build(int p,int l,int r){
t[p].l=l;t[p].r=r;
if(l==r)return ;
int mid=l+r>>1;
build(p*2,l,mid);build(p*2+1,mid+1,r);
return ;
}
void asi(int p,int l,int r,int k){
if(l<=t[p].l&&t[p].r<=r) return t[p].maxv=max(t[p].maxv,k),void();
int mid=t[p].l+t[p].r>>1;
if(l<=mid)asi(p*2,l,r,k);
if(mid<r) asi(p*2+1,l,r,k);
return ;
}
void dfs(int p,int ca){
if(t[p].l==t[p].r)return ans[t[p].l]=max(ca,t[p].maxv),void();
int mid=t[p].l+t[p].r>>1;
dfs(p*2,max(ca,t[p].maxv));dfs(p*2+1,max(ca,t[p].maxv));
return ;
}
int main(){
int k;cin>>k;
string s;cin>>s;
for(int i=1,l=0,r=0;i<s.size();i++){
if(i<=r&&z[i-l]<r-i+1)z[i]=z[i-l];
else{
z[i]=max(0,r-i+1);
while(i+z[i]<s.size()&&s[z[i]]==s[i+z[i]])z[i]++;
}
if(r<i+z[i]-1)l=i,r=i+z[i]-1;
}
build(1,0,s.size()-1);
for(int i=1;i<s.size();i++){
if(i<=z[i]){
int dt=(z[i]-1)-i+1;
asi(1,i,i+z[i]-dt-1,z[i]-dt);
asi(1,i+z[i]-dt,i+z[i]-1,i+z[i]-dt-1);
}
else asi(1,i,i+z[i]-1,i);
}
dfs(1,0);
ll asdf=0;
for(int i=1;i<s.size();i++)asdf+=ans[i];
cout<<asdf;
return 0;
}
P4824 [USACO15FEB] Censoring S
删除后会合出来新的串这一点很恶心,但是别忘了我们有快速判相等的神器哈希。
我们维护一个栈,按照长度 base^i mod 类的单模哈希,于是可以速算前 \(m\) 个字符的哈希,这指向栈顶和第 \(m\) 个元素的两个指针是可以很快的跳的。于是如果前 \(m\) 个字符哈希和目标串相等,就弹出前 \(m\) 个,重复此操作,最后输出站内元素即可。
当然我知道你不想用哈希,那我们还可以用 ACAM,然后搞2个栈维护:ACAM 目前跑到字典树上的哪个点和已经跑过且没被删除的字符(答案栈)。
每次碰到有结尾标记的点,就让两个栈弹出目标串长度个数就行了,同时跟踪主串的指针也要回退(因为主串已经变了)。
当然这样有点大材小用,因为我们只需要给 ACAM 里面插入一个目标串。如果题面要求删去多个串,ACAM 将是更好的选择。
code
Show me the code


 浙公网安备 33010602011771号
浙公网安备 33010602011771号