KMP 算法
前言
板子挺好记,也就这一个好记了。
1. 概述
KMP 算法,即 Knuth-Morris-Pratt 字符串查找算法,是一个用于在一个字符串中查找另一个字符串的算法。并不是某一些奇怪英文单词的简写,而是三个人名的首字母。
KMP 算法的时间复杂度十分优秀,为 \(O(n)\) 级,\(n\) 为待查找的字符串的长度。
2. 一些定义
-
主串:字符串整体。
-
子串:主串中连续的一部分。
-
模式串:待匹配的字符串整体,一般来说短于主串。
-
模式串匹配:在主串中找到与模式串相同的子串,并返回其出现位置(一个或多个)。
-
前缀子串:从字符串开头到字符串任意位置的子串,如图:
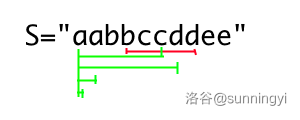
在图中,绿色部分包括的子串均为合法的前缀子串,红色部分为不合法的前缀子串。 -
后缀子串:从字符串最后一个字符到字符串任意位置的子串,如图:
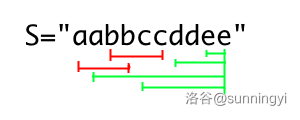
在图中,绿色部分包括的子串均为合法的后缀子串,红色部分子串为不合法的后子串。 -
在这篇文章中,程序默认将两个新输入主串和模式串头部加入一个
' '以保证第一个字符在下标 \(1\) 的位置。为了计算方便,作者的代码中 \(j\) 均从 \(0\) 开始,但访问字符串的时候使用 \(j+1\)
3. 原理及实现
在研究优化算法之前,我们先来看一看暴力的字符串匹配算法如何写:
首先我们准备两个指针,分别指向主串和模式串目前要匹配的位置,我们把这两个指针分别称为主串指针和模式串指针。
此时这两个地方的两个字符之间有两种情况:
- 两个字符相同,那么此时这个字符被成功匹配,将两个指针后移一位,继续匹配下一个字符。
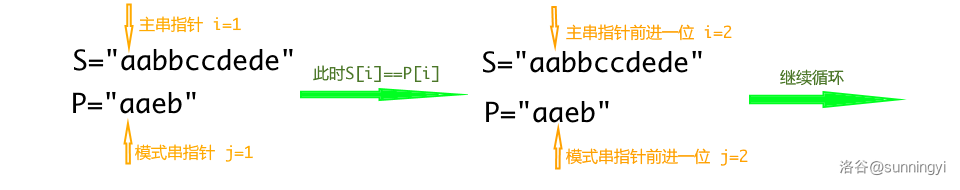
- 两个字符不同,这时模式串指针要退回模式串头重新开始匹配,主串指针要退回到第一个匹配上的位置的后一个位置去与模式串继续匹配(因为 “第一个匹配上的位置” 已经确认不会匹配上模式串了)。

而 "第一个匹配上的位置的后一个位置" 可以通过 \(i\) 和 \(j\) 简单算出,为 \(i-j+1+1\)。
如果两个字符相同后两个字符串被完全匹配(模式串指针到了模式串末尾),那么输出这个模式串在主串中出现的起始位置,之后模式串指针退回模式串头重新开始匹配,主串指针要退回到第一个匹配上的位置的后一个位置去与模式串继续匹配。
于是可以很简单的写出如下代码:
int main(){
string a,b;
cin>>a>>b;
int n=a.size(),m=b.size();
a=' '+a;//将两个字符串的开始下标都变成 1 以方便操作
b=' '+b;
for(int i=1,j=0;i<=n;i++){//注意这里的模式串指针从 0 开始(从 1 开始也可以,个人习惯)
if(a[i]!=b[j+1]){//如果不匹配
i=i-j+1;//主串指针退回,这里少的一个 +1 操作体现在 for 循环框架中的 i++
j=0;//模式串指针退回到模式串头部
}
if(a[i]==b[j+1]){//如果匹配
j++;//模式串指针前进一位
//主串指针前进一位的 +1 操作体现在 for 循环框架中的 i++
}
if(j==m){//如果全部匹配上了
cout<<i-j+1<<'\n'; //输出第一个匹配上的位置
i=i-j+1; //主串指针退回
j=0;//模式串指针退回
}
}
return 0;
}
这个程序的时间复杂度很明显是 \(O(nm)\) 的,虽然它也可以通过 KMP 的模板题。
为什么要先介绍这个框架呢,因为 KMP 算法只需要在框架上稍作修改便可写出。
回看我们上面的程序,可以发现它在某些情况下有些笨,例如这样的情况:
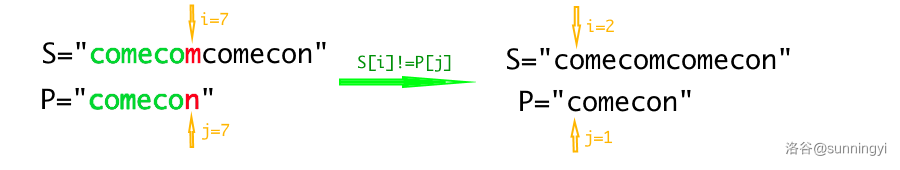
当然,现实生活中很少有这样的字符串匹配的例子,因此我们可能感受不到 KMP 算法的速度。但我们不能保证出题人不故意造阴间数据卡暴力算法。
在上面的例子中,KMP 算法会这样移动两个指针:
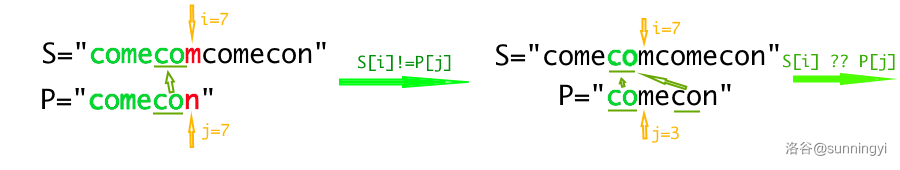
当主串 \(S\) 和模式串 \(P\) 在 \(i=7\) 位置失配时,我们可以确定模式串中 \([1,6]\) 区间内的字符串和主串中的 \([1,6]\) 是匹配的,也就是左边部分被染绿的子串。
我们发现在已经匹配的子串 \(\texttt{comeco}\) 中,存在最长的后缀子串 \(\texttt{co}\) 等于前缀子串 \(\texttt{co}\)。
于是我们不让 \(i\) 移动,让 \(j\) 移动到相同的前缀子串后一个的位置,也就是 \(\texttt{comecon}\) 中 \(\texttt{m}\) 的位置,继续与主串匹配,如右边部分。这便是 KMP 算法与暴力不同的地方。
有个问题,不移动 \(i\),怎样保证不会漏下匹配某一些子串呢?
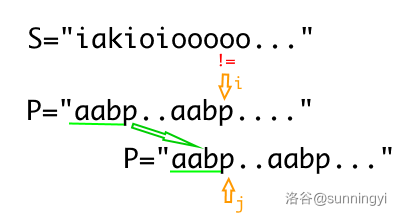
我们用反证法证明,假设我们根据以上的方法跳转,跳转后在跳转过去的某一个位置开始依然可以匹配模式串,设这个地方的下标为 \(k\)。
表现在图中如下:
既然从 \(k\) 开始可以匹配模式串(虽然在图中是不行的,只是举例),这意味着最起码前三个 \(\texttt{???}=\texttt{eco}\)。由于我们在失配处确定了 \(\texttt{comeco}=\texttt{??????}\)。也就是说后三个 \(\texttt{???}=\texttt{eco}\)。
所以可以确定,左右这两个 \(\texttt{???}\) 是一样的,于是它们边可以成为一对长度为 \(3\) 的后缀子串等于前缀子串。
但是我们转移的时候是利用的 “已经匹配的子串 \(\texttt{comeco}\) 中,存在最长的后缀子串 \(\texttt{co}\) 等于前缀子串 \(\texttt{co}\)。”最长的后缀字串等于前缀子串的长度是 \(2\),这与我们由假设推出的结论矛盾!
于是假设不成立,即跳转过去的某一个位置开始没有一处可以匹配模式串,故不会漏下匹配某一些子串。
既然我们确定了这样移动指针进行匹配的正确性,接下来我们就要求解出 “让 \(j\) 移动到相同的前缀子串后一个的位置” 了。我们设 \(j\) 这样移动移动到的位置为 \(next_j\)。
首先可以发现,\(next_j\) 的值仅与模式串有关,与主串无关。
我们考虑模式串下标为 \(1\) 处,\(next_1\) 的值。很明显,由于指向了模式串的第一个字符,因此如果此处与主串失配了,它也只能跳转到模式串的开头,即 \(next_1=0\)。
之后,我们设 \(next_i=j\),如果我们能通过这个条件推导出 \(next_{i+1}\) 的值,那么我们就可以通过递推求解处任意的 \(next_i\) 的值。
我们想想,\(next_i=j\) 在 KMP 算法中表示什么意思。
它代表,如果模式串在 \(i\) 处于主串失配,则可以将 \(i\) 跳转到 \(next_i\) 即 \(j\) 的位置继续匹配。
根据我们上面的例子,这意味着字符串中 \([1,j-1]\) 与 \([i-j+1,i-1]\) 就是我们所说的 “最长的后缀子串等于前缀子串”,即:
其中 \(P_iP_j\) 表示字符合并成字符串。
那么,我们要求解 \(next_{i+1}\),就要考虑 \(P_i\) 和 \(P_j\) 两者的关系了。
- \(P_i=P_j\)
这时情况很简单了,当 \(P_i=P_j\),也就意味着 \(P_1P_2\cdots P_{j}=P_{i-j+1}P_{i-j+2}\cdots P_{i}\)。显然:\[next_{i+1}=next_{i}+1 \]如下图: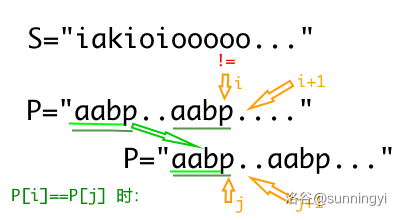
在图中,\(P_i=P_j\),此时如果主串和模式串在 \(i+1\) 处失配,则 \(i\) 可以跳转到 \(j+1\) 的位置继续匹配,也就是 \(next_i+1\)。 - \(P_i\ne P_j\)
这时候,我们只需要让 \(j\) 不停地被 \(next_j\) 赋值,最后如果找到了一个 \(j\) 使得 \(P_j=P_i\) 则\[next_{i+1}=j+1 \]如果没有找到,则 \(next_{i+1}=0\)
为何这样做呢?我们一点一点理解:
首先可以证明,在 \(j\) 到模式串头之前,无论 \(j\) 不停地被 \(next_j\) 赋值多少次,总会有:\[P_1P_2\cdots P_{j-1}=P_{i-j+1}P_{i-j+2}\cdots P_{i-1} \]也就是下图所示的情况:
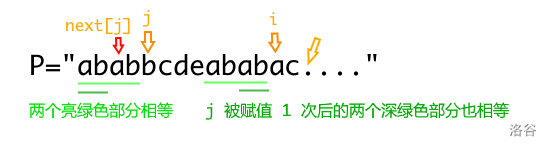
作者不会严谨证明,感性理解一下。
此时如果我们如果找到了一个 \(j\) 使得 \(P_j=P_i\) 如下图:

此时根据我们的定义 \(next_{i+1}\) 的值就是 \(j+1\)。
既然这两个指针处字符仅有的两个情况都可以推出下一个 \(next_{i+1}\) 的值,那么我们就可以直接用递推求解出任意的 \(next_i\)。
4. 完整代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rd read()
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
ll nxt[(int)1e6+5];
int main(){
string a,b;
cin>>a>>b;
int n=a.size(),m=b.size();
a=' '+a;//都加上一个 ' ' 便于处理
b=' '+b;
nxt[1]=0;
for(int i=2,j=0;i<=m;i++){
while(j&&b[i]!=b[j+1])j=nxt[j];//不匹配,不断赋值找到 b[i]=b[j],这里 b[j+1] 的原因请看定义中的最后一条
if(b[i]==b[j+1])j++;//相等时就是答案就是下一个
nxt[i]=j;//直接赋值
}
for(int i=1,j=0;i<=n;i++){
while(j&&a[i]!=b[j+1])j=nxt[j];//不匹配了,使用 nxt 数组回到一个位置让主串等于模式串
//为什么可以一直回退呢?因为如果此时的 b[j] != a[i] 则这里没有可能完全匹配
if(a[i]==b[j+1])j++;//把模式串指针向前移动继续匹配
if(j==m){//如果移动到了模式串头部,则证明完全匹配,直接输出
cout<<i-j+1<<'\n';
j=nxt[j];//这时回退时只需要回退 1 次。
}
}
return 0;
}
5. KMP 算法的应用
5.1 判断主串和模式串相等
这个不用多说了,KMP 的本职工作。
5.2 求解组成一个字符串的最小循环节长度
设要判断的字符串的长度为 \(n\),则答案为 \(n-next_n\)。
例题:
洛谷搬运 BOI 2009 / P4391
洛谷搬运 UVA 10298
例题 \(2\) 示例代码:
#define rd read()
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
using namespace std;
typedef long long ll;
ll read(){
ll x=0,f=1;
char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
return x*f;
}
ll nxt[(int)1e6+5];
int main(){
cin.tie(0);
ios::sync_with_stdio(0);
int n=0;
string s;
while(1){
cin>>s;
if(s==".")return 0;
fill(nxt,nxt+n,0);
n=s.size();
s=' '+s;
for(int i=2,k=0;i<=n;i++){
while(k&&s[i]!=s[k+1])k=nxt[k];
if(s[i]==s[k+1])k++;
nxt[i]=k;
}
if(n%(n-nxt[n])==0)cout<<n/(n-nxt[n])<<'\n';
else cout<<1<<'\n';
}
return 0;
}
5.3 AC 自动机
在这里.
迁移自洛谷

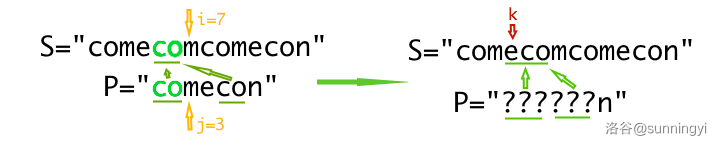

 浙公网安备 33010602011771号
浙公网安备 33010602011771号