Manacher 算法

前言

掌管回文串的神。

1. 原理

manacher 算法专门用来解决字符串中的回文串一类问题，由于其英文读音，音译其为 “马拉车” 算法。
manacher 算法可以在 \(O(n)\) 时间复杂度和 \(O(n)\) 空间复杂度内处理出字符串中以任意位置为回文中心的回文串长度，当然可以顺便求出这个字符串中的最长回文串。

在细说原理之前，先来明确几个概念：

• 回文串的回文中心：
  对于回文串，可以将其按照长度奇偶性分为长度为奇数的回文串，即 奇回文串 和长度为偶数的回文串，即 偶回文串。对于两种回文串都有自身的 回文中心，如下图：

  

• 回文串的回文半径：
  对于奇回文串，其回文半径 \(r=\dfrac{字符串长度-1}{2}\)。对于偶回文串，其回文半径 \(r=\dfrac{字符串长度}{2}\)。如下图：

  

从上面的回文串相关的概念可以发现，回文串内部居然还分为不同的种类，如果还要在程序中分类讨论过于麻烦。于是 manacher 算法做的第一件事就是将给定的字符串进行修改使其无需分类讨论回文串。
怎么修改呢？manacher 算法采用将原串中插入字符的方式，具体如下：

在上面的例子中，^ 用来标记字符串开头，$ 用来标记字符串结尾。
当然，可以插入的不只是这三种字符。但插入这些字符有什么用呢？
接着沿用上面的例子：

可以发现，进行处理后的字符串不仅统一了奇偶回文串回文中心的位置（统一在字符上而不是两个字符之间），便于之后的枚举，也将串长变成了回文半径。

接下来我们讨论回文半径的求法，考虑下面这个处理后的字符串：

我们将以每个字符为回文中心所能形成的最长的回文串标记出来（你可以形象的理解为种蘑菇）：

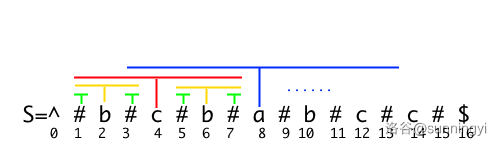
观察红色蘑菇包裹的区域，可以发现：在一个较大的回文串中，以回文中心为对称点，两个子串的回文情况是相同的。
那么，我们就可以用已经扩展好的大回文串，对称过来一侧的回文情况就可以求解出另一侧。
但是有一种情况特殊：观察 \(8\) 号字符 \(\texttt{a}\) 和 \(4\) 号字符 \(\texttt{c}\)，虽然 \(\texttt{c}\) 这个回文中心在 \(\texttt{a}\) 的回文半径里，但是 \(\texttt{c}\) 包括的回文串区域超出了 \(\texttt{a}\) 的区域，此时还能直接对称吗？
一定是不能的，因为对称性仅在一个回文串内部有效，此时我们要截断 \(\texttt{c}\) 的回文半径使它对称过来后在 \(\texttt{a}\) 的回文半径内部。对称后只能通过接着向左右枚举来扩展回文长度。
那么现在我们想知道：如何 “对称过来一侧的回文情况” 呢？
我们设此时已知能向右覆盖的范围最大的回文串（也就是上图的以 \(\texttt{a}\) 为回文中心的字符串）的回文中心的下标为 \(ctr\)，定义以下标 \(k\) 为回文中心的回文串，其最大回文半径存储在数组 \(r[k]\) 中，这个回文串向右覆盖到的最远下标为 \(cur\)，显然 \(cur=r[ctr]+ctr\)。
对于一个将要对称过来求解的回文中心下标 \(i\)（显然 \(ctr<i \le cur\)），如果其回文串包括的范围完全在大回文串的范围内，有：

\[r[i]=r[ctr-(i-ctr)]=r[ctr\times 2 -i] \]

如果超出了回文串的范围，有：

\[r[i]=cur-i \]

显然两者只需取最小值即可。

由于是根据对称求解的回文半径，可能包括的不全，因此还要用一个 while 循环尽可能往两边扩展。
如果扩展出的回文串成为了目前 能向右覆盖的范围最大的回文串，即（\(cur<i+r[i]\)），那么更新 \(cur,ctr\) 的值，继续对称求解。

那么如果对称求解时枚举的 \(i\) 超出了 \(cur\) 的范围怎么办？只能将 \(r[i]=0\)，然后自己扩展了。

2. 代码实现

由于我们要向原串中添加某些字符，且添加字符的长度往往等于原串的长度，所以 \(r\) 数组的大小记得开原串长度的两倍多一点。
以下使用 string 存储字符串，变量的命名与上文相同，string s 存储原串，string ms 存储添加字符后的字符串。

#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
	ll x=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
int r[22000055];
int manacher(string s){
	memset(r,0,sizeof r);
	string ms="^#";
	for(int i=0;i<s.size();i++){//添字符
		ms+=s[i];
		ms+='#';
	}
	ms=ms+'$';
//	cout<<ms<<'\n';
	int cur=-1,ctr=-1;//初始化最右边界，回文中心
	int ans=0;
	for(int i=0;i<ms.size();i++){
		if(i<=cur){//在当前最右串范围内
			r[i]=min(cur-i,r[2*ctr-i]);//对称处理
		}
		else{
			r[i]=1;//如果不在，只能自己扩展
		}
		while (ms[i+r[i]+1]==ms[i-r[i]-1])r[i]++;//自己尝试扩展
		if(i+r[i]>cur){//如果比当前最右串还右
			ctr=i;//更新
			cur=i+r[i];
		}
		ans=max(r[i],ans);//记录最大回文半径，即最大回文串长
	}
	return ans;
}
int main(){
	
	string s;
	cin>>s; 
	cout<<manacher(s);
	
	return 0;
}

3. 复杂度

时间复杂度 \(O(n)\)，空间复杂度 \(O(n)\)。
引用 OIwiki 上的话：

因为在计算一个特定位置的答案时我们总会运行朴素算法，所以一眼看去该算法的时间复杂度为线性的事实并不显然。

然而更仔细的分析显示出该算法具有线性复杂度。此处我们需要指出，计算 Z 函数的算法和该算法较为类似，并同样具有线性时间复杂度。

实际上，注意到朴素算法的每次迭代均会使 r 增加 1，以及 r 在算法运行过程中从不减小。这两个观察告诉我们朴素算法总共会进行 \(O(n)\) 次迭代。

Manacher 算法的另一部分显然也是线性的，因此总复杂度为 \(O(n)\)。

---

迁移自洛谷