洛谷P4781 【模板】拉格朗日插值
https://www.luogu.org/problemnew/show/P4781
https://www.cnblogs.com/zj75211/p/8028165.html讲的很清楚了
拉格朗日插值
设给定点为$(x_0,y_0)$到$(x_{n-1},y_{n-1})$,求经过它们的多项式F
公式:$F(x)=\sum_{i=0}^{n-1}y_i\prod_{j=0,j\ne i}^{n-1}\frac{x-x_j}{x_i-x_j}$
对于此题,不需要真的把多项式求出来,直接在计算过程中把给定数带入求值就行($O(n^2)$)

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<vector> 5 using namespace std; 6 #define fi first 7 #define se second 8 #define mp make_pair 9 #define pb push_back 10 typedef long long ll; 11 typedef unsigned long long ull; 12 const int md=998244353; 13 int n,K,ans; 14 int x[2011],y[2011]; 15 int poww(int a,int b) 16 { 17 int ans=1; 18 for(;b;b>>=1,a=ll(a)*a%md) 19 if(b&1) 20 ans=ll(a)*ans%md; 21 return ans; 22 } 23 int main() 24 { 25 int i,j,t1,t2; 26 scanf("%d%d",&n,&K); 27 for(i=0;i<n;++i) 28 scanf("%d%d",x+i,y+i); 29 for(i=0;i<n;++i) 30 { 31 t1=t2=1; 32 for(j=0;j<n;++j) 33 if(j!=i) 34 { 35 t1=ll(t1)*(K-x[j]+md)%md; 36 t2=ll(t2)*(x[i]-x[j]+md)%md; 37 } 38 ans=(ans+ll(t1)*poww(t2,md-2)%md*y[i])%md; 39 } 40 printf("%d\n",ans); 41 return 0; 42 }
真的有必要求出多项式的话,可以先算出全部$(x-x_i)$的积,每次把它除以一项,来得到各个$l_i(x)$
这个“除以一项”怎么搞?就相当于模拟一个大除法
设除完$(x-x_i)$的结果为A(x),各项系数为$a_i$,除之前为B(x),各项系数为$b_i$,令$y=x_i$
则$b_{n+1}=a_n$,$b_n=a_{n-1}-a_ny$,$b_{n-1}=a_{n-2}-a_{n-1}y$,...
$a_n=b_{n+1}$,$a_{n-1}=b_n+a_ny$,$a_{n-2}=b_{n-1}+a_{n-1}y$,...
还是$O(n^2)$
当然,此题这么做要慢一点;不过这个在某些情况下有用,由于多项式求值可以O(n)完成

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 #include<vector> 5 using namespace std; 6 #define fi first 7 #define se second 8 #define mp make_pair 9 #define pb push_back 10 typedef long long ll; 11 typedef unsigned long long ull; 12 const int md=998244353; 13 int n,K,ans; 14 int x[2011],y[2011]; 15 int an1[2011],tt1[2011],tt2[2011]; 16 //tt1维护所有(x-x_i)的积,an1维护答案 17 int poww(int a,int b) 18 { 19 int ans=1; 20 for(;b;b>>=1,a=ll(a)*a%md) 21 if(b&1) 22 ans=ll(a)*ans%md; 23 return ans; 24 } 25 int main() 26 { 27 int i,j,t2; 28 scanf("%d%d",&n,&K); 29 for(i=0;i<n;++i) 30 scanf("%d%d",x+i,y+i); 31 tt1[0]=1; 32 for(i=0;i<n;++i) 33 { 34 tt1[i+1]=tt1[i]; 35 for(j=i;j>=1;--j) 36 tt1[j]=(ll(tt1[j])*(md-x[i])+tt1[j-1])%md; 37 tt1[0]=ll(tt1[0])*(md-x[i])%md; 38 } 39 for(i=0;i<n;++i) 40 { 41 tt2[n-1]=tt1[n]; 42 for(j=n-2;j>=0;--j) 43 tt2[j]=(tt1[j+1]+ll(tt2[j+1])*x[i])%md; 44 t2=1; 45 for(j=0;j<n;++j) 46 if(j!=i) 47 t2=ll(t2)*(x[i]-x[j]+md)%md; 48 t2=ll(poww(t2,md-2))*y[i]%md; 49 for(j=0;j<n;++j) 50 an1[j]=(an1[j]+ll(t2)*tt2[j])%md; 51 } 52 ans=0; 53 for(j=n-1;j>=0;--j) 54 ans=(ll(ans)*K+an1[j])%md; 55 printf("%d\n",ans); 56 return 0; 57 }
重心拉格朗日插值
https://blog.csdn.net/qq_35649707/article/details/78018944
https://zh.wikipedia.org/wiki/%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E6%8F%92%E5%80%BC%E6%B3%95
设$l(x) = \prod_j(x-x_j)$
$\omega_i= \frac{1}{\prod\limits_{j\not = i}(x_i-x_j)}$
则$F(x)=l(x)\sum_i\frac{\omega _i}{x-x_i}y_i$(的确是对的,过程省略了)
这个东西的好处是,在增加一个新点的坐标时,只需要O(n)的时间来更新解,不需要$O(n^2)$重新计算整个解(具体方法先鸽着)
还有一个公式(重心拉格朗日插值(第二型))
将$g(x)=1$在对原多项式给出的所有x坐标处用以上方法插值,得到$l(x)\sum_i\frac{\omega _i}{x-x_i}=1$(并不知道怎么想出来的)
所以$F(x)=\frac{F(x)}{1}=\frac{\sum_i\frac{\omega _i}{x-x_i}y_i}{\sum_i\frac{\omega _i}{x-x_i}}$(暂时不知道有什么特别的用处)
其他资料https://www.cnblogs.com/ECJTUACM-873284962/p/6833391.html

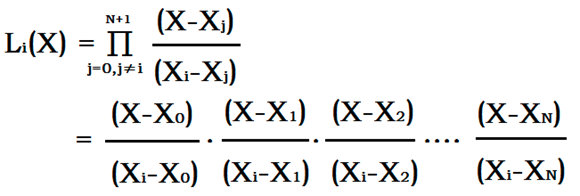
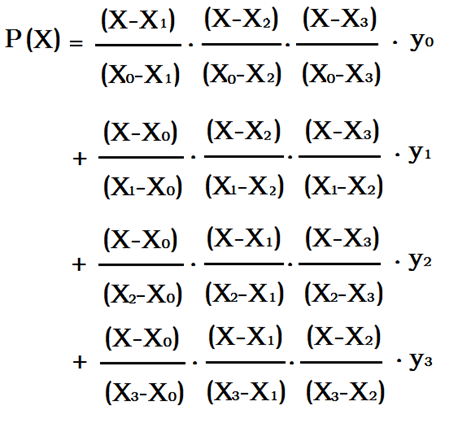


 浙公网安备 33010602011771号
浙公网安备 33010602011771号