拉格朗日插值法(图文详解)
在数值分析中,拉格朗日插值法是以法国十八世纪数学家约瑟夫·拉格朗日命名的一种多项式插值方法。许多实际问题中都用函数来表示某种内在联系或规律,而不少函数都只能通过实验和观测来了解。如对实践中的某个物理量进行观测,在若干个不同的地方得到相应的观测值,拉格朗日插值法可以找到一个多项式,其恰好在各个观测的点取到观测到的值。这样的多项式称为拉格朗日(插值)多项式。数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。拉格朗日插值法最早被英国数学家爱德华·华林于1779年发现[1],不久后(1783年)由莱昂哈德·欧拉再次发现。1795年,拉格朗日在其著作《师范学校数学基础教程》中发表了这个插值方法,从此他的名字就和这个方法联系在一起[2]。
对于给定的若n+1个点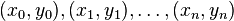 ,对应于它们的次数不超过n的拉格朗日多项式
,对应于它们的次数不超过n的拉格朗日多项式 只有一个。如果计入次数更高的多项式,则有无穷个,因为所有与
只有一个。如果计入次数更高的多项式,则有无穷个,因为所有与 相差
相差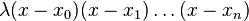 的多项式都满足条件。例子:
的多项式都满足条件。例子:

以及
 各穿过对应的一点,并在其它的三个点的x值上取零。
各穿过对应的一点,并在其它的三个点的x值上取零。定义
对某个多项式函数,已知有给定的k + 1个取值点:
其中 对应着自变量的位置,而
对应着自变量的位置,而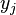 对应着函数在这个位置的取值。
对应着函数在这个位置的取值。
假设任意两个不同的xj都互不相同,那么应用拉格朗日插值公式所得到的拉格朗日插值多项式为:
其中每个 为拉格朗日基本多项式(或称插值基函数),其表达式为:
为拉格朗日基本多项式(或称插值基函数),其表达式为:
拉格朗日基本多项式 的特点是在
的特点是在 上取值为1,在其它的点
上取值为1,在其它的点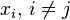 上取值为0。
上取值为0。
范例
假设有某个二次多项式函数 ,已知它在三个点上的取值为:
,已知它在三个点上的取值为:
要求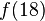 的值。
的值。
首先写出每个拉格朗日基本多项式:
然后应用拉格朗日插值法,就可以得到 的表达式(
的表达式( 为函数
为函数 的插值函数):
的插值函数):
此时代入数值 就可以求出所需之值:
就可以求出所需之值: 。
。
证明
存在性
对于给定的k+1个点: ,拉格朗日插值法的思路是找到一个在一点
,拉格朗日插值法的思路是找到一个在一点 取值为1,而在其他点取值都是0的多项式
取值为1,而在其他点取值都是0的多项式 。这样,多项式
。这样,多项式 在点
在点 取值为
取值为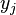 ,而在其他点取值都是0。而多项式
,而在其他点取值都是0。而多项式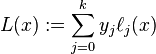 就可以满足
就可以满足
在其它点取值为0的多项式容易找到,例如:
它在点 取值为:
取值为: 。由于已经假定
。由于已经假定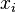 两两互不相同,因此上面的取值不等于0。于是,将多项式除以这个取值,就得到一个满足“在
两两互不相同,因此上面的取值不等于0。于是,将多项式除以这个取值,就得到一个满足“在 取值为1,而在其他点取值都是0的多项式”:
取值为1,而在其他点取值都是0的多项式”:
这就是拉格朗日基本多项式。
唯一性
次数不超过k的拉格朗日多项式至多只有一个,因为对任意两个次数不超过k的拉格朗日多项式: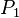 和
和 ,它们的差
,它们的差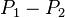 在所有k+1个点上取值都是0,因此必然是多项式
在所有k+1个点上取值都是0,因此必然是多项式 的倍数。因此,如果这个差
的倍数。因此,如果这个差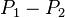 不等于0,次数就一定不小于k+1。但是
不等于0,次数就一定不小于k+1。但是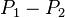 是两个次数不超过k的多项式之差,它的次数也不超过k。所以
是两个次数不超过k的多项式之差,它的次数也不超过k。所以 ,也就是说
,也就是说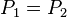 。这样就证明了唯一性[4]。
。这样就证明了唯一性[4]。
几何性质
拉格朗日插值法中用到的拉格朗日基本多项式 (由某一组
(由某一组 确定)可以看做是由次数不超过n的多项式所组成的线性空间:
确定)可以看做是由次数不超过n的多项式所组成的线性空间:![{\mathbb {K}}_{n}[X]](http://upload.wikimedia.org/math/9/4/a/94a1ed21235d59c5b5f5960c561d41a3.png) 的一组基底。首先,如果存在一组系数:
的一组基底。首先,如果存在一组系数: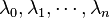 使得,
使得,
 ,
,
那么,一方面多项式P是满足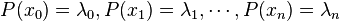 的拉格朗日插值多项式,另一方面P是零多项式,所以取值永远是0。所以
的拉格朗日插值多项式,另一方面P是零多项式,所以取值永远是0。所以
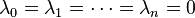 。
。
这证明了 是线性无关的。同时它一共包含n+1个多项式,恰好等于
是线性无关的。同时它一共包含n+1个多项式,恰好等于![{\mathbb {K}}_{n}[X]](http://upload.wikimedia.org/math/9/4/a/94a1ed21235d59c5b5f5960c561d41a3.png) 的维数。所以
的维数。所以 构成了
构成了![{\mathbb {K}}_{n}[X]](http://upload.wikimedia.org/math/9/4/a/94a1ed21235d59c5b5f5960c561d41a3.png) 的一组基底。
的一组基底。
拉格朗日基本多项式作为基底的好处是所有的多项式都是齐次的(都是n次多项式)。
优点与缺点
拉格朗日插值法的公式结构整齐紧凑,在理论分析中十分方便,然而在计算中,当插值点增加或减少一个时,所对应的基本多项式就需要全部重新计算,于是整个公式都会变化,非常繁琐[5]。这时可以用重心拉格朗日插值法或牛顿插值法来代替。此外,当插值点比较多的时候,拉格朗日插值多项式的次数可能会很高,因此具有数值不稳定的特点,也就是说尽管在已知的几个点取到给定的数值,但在附近却会和“实际上”的值之间有很大的偏差(如右下图)[6]。这类现象也被称为龙格现象,解决的办法是分段用较低次数的插值多项式。
重心拉格朗日插值法
重心拉格朗日插值法是拉格朗日插值法的一种改进。在拉格朗日插值法中,运用多项式
可以将拉格朗日基本多项式重新写为:
上面的表达式可以简化为:
于是拉格朗日插值多项式变为:
即所谓的重心拉格朗日插值公式(第一型)或改进拉格朗日插值公式。它的优点是当插值点的个数增加一个时,将每个 都除以
都除以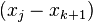 ,就可以得到新的重心权
,就可以得到新的重心权 ,计算复杂度为
,计算复杂度为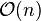 ,比重新计算每个基本多项式所需要的复杂度
,比重新计算每个基本多项式所需要的复杂度 降了一个量级。
降了一个量级。
将以上的拉格朗日插值多项式用来对函数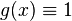 插值,可以得到:
插值,可以得到:
因为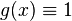 是一个多项式。
是一个多项式。
因此,将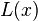 除以
除以 后可得到:
后可得到:
这个公式被称为重心拉格朗日插值公式(第二型)或真正的重心拉格朗日插值公式。它继承了(1)式容易计算的特点,并且在代入x值计算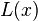 的时候不必计算多项式
的时候不必计算多项式 [7]。它的另一个优点是,结合切比雪夫节点进行插值的话,可以很好地模拟给定的函数,使得插值点个数趋于无穷时,最大偏差趋于零[7]。同时,重心拉格朗日插值结合切比雪夫节点进行插值可以达到极佳的数值稳定性。第一型拉格朗日插值是向后稳定的,而第二型拉格朗日插值是向前稳定的,并且勒贝格常数很小[9]。
[7]。它的另一个优点是,结合切比雪夫节点进行插值的话,可以很好地模拟给定的函数,使得插值点个数趋于无穷时,最大偏差趋于零[7]。同时,重心拉格朗日插值结合切比雪夫节点进行插值可以达到极佳的数值稳定性。第一型拉格朗日插值是向后稳定的,而第二型拉格朗日插值是向前稳定的,并且勒贝格常数很小[9]。
参考来源
- ^ E. Waring. Problems Concerning Interpolations. Philosophical Transactions of the Royal Society of London. 1779, 69: 59–67.
- ^ (英文)E. Meijering. A chronology of interpolation: From ancient astronomy to modern signal and image processing,. Proceedings of the IEEE: 323.
- ^ (英文)Julius Orion Smith III. Lagrange_Interpolation. Center for Computer Research in Music and Acoustics (CCRMA), Stanford University.
- ^ 冯有前,《数值分析》,第63页
- ^ 李庆扬,《数值分析》第4版,第31页
- ^ 冯有前,《数值分析》,第64页
- ^ 7.0 7.1 7.2 7.3 Jean-Paul Berrut, Lloyd N. Trefethen. Barycentric Lagrange Interpolation. SIAM Review. 2004, 46 (3): 501–517.doi:10.1137/S0036144502417715.
- ^ 王兆清,李淑萍,唐炳涛. 一维重心型插值:公式、算法和应用. 山东建筑大学学报. 2007, 22 (5): 447–453.
- ^ NICHOLAS J. HIGHAM. The numerical stability of barycentric Lagrange Interpolation. IMA Journal of Numerical Analysis. 2004, 24 (4): 547–556.
- (中文)李庆扬,王能超,易大义. 《数值分析》第4版. 清华大学出版社. 2001. ISBN 7-302-04561-5.
- (中文)冯有前. 《数值分析》. 清华大学出版社. 2001. ISBN 7-810-82495-3.
- (中文)拉格朗日插值多项式. 太原理工大学.
作 者:Angel_Kitty
出 处:https://www.cnblogs.com/ECJTUACM-873284962/
关于作者:阿里云ACE,目前主要研究方向是Web安全漏洞以及反序列化。如有问题或建议,请多多赐教!
版权声明:本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文链接。
特此声明:所有评论和私信都会在第一时间回复。也欢迎园子的大大们指正错误,共同进步。或者直接私信我
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是作者坚持原创和持续写作的最大动力!
欢迎大家关注我的微信公众号IT老实人(IThonest),如果您觉得文章对您有很大的帮助,您可以考虑赏博主一杯咖啡以资鼓励,您的肯定将是我最大的动力。thx.

我的公众号是IT老实人(IThonest),一个有故事的公众号,欢迎大家来这里讨论,共同进步,不断学习才能不断进步。扫下面的二维码或者收藏下面的二维码关注吧(长按下面的二维码图片、并选择识别图中的二维码),个人QQ和微信的二维码也已给出,扫描下面👇的二维码一起来讨论吧!!!

欢迎大家关注我的Github,一些文章的备份和平常做的一些项目会存放在这里。




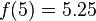

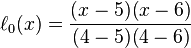
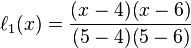

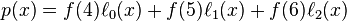
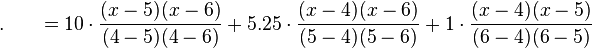
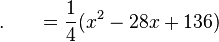

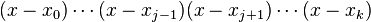
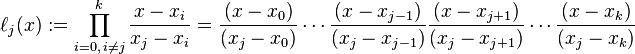
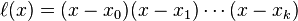

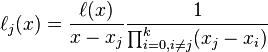




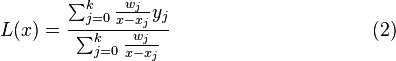

 浙公网安备 33010602011771号
浙公网安备 33010602011771号