平衡型运输问题：基可行解的变量数

平衡型运输问题是运输问题（Transportation Problem）的标准型，其核心特征是 总供给量等于总需求量，即满足严格的产销平衡条件：

\[\sum_{i=1}^{m} a_i = \sum_{j=1}^{n} b_j \]

其中，\(a_i\) 表示第 \(i\) 个产地（或供货点）的供给能力，即可提供的货物总量；\(b_j\) 表示第\(j\) 个销地（或需求点）的需求数量，即需要接收的货物总量。该等式反映了整个运输系统的资源守恒原则——供给端和需求端在总体上完全匹配，没有盈余或短缺。换言之，所有产地提供的货物恰好能满足所有销地的需求，从而构成一个封闭平衡系统。在这种条件下，运输问题可通过线性规划形式求解，其数学结构清晰、约束线性独立性高，是研究最优化调度与成本最小化的基础模型。

---

---

一、平衡型运输问题数学模型的特点

设系统中共有 \(m\) 个产地（供应点）和 \(n\) 个销地（需求点），其数学模型可表示为以下线性规划形式：

\[\begin{aligned} \text{Minimize} \quad & Z = \sum_{i=1}^{m} \sum_{j=1}^{n} c_{ij} x_{ij} \\[8pt] \text{subject to} \quad & \sum_{j=1}^{n} x_{ij} = a_i, \quad i = 1, 2, \dots, m \\[8pt] & \sum_{i=1}^{m} x_{ij} = b_j, \quad j = 1, 2, \dots, n \\[8pt] & x_{ij} \ge 0, \quad \forall i,j \end{aligned} \]

其中：

• \(x_{ij}\)：表示从第 \(i\) 个产地运输到第 \(j\) 个销地的货物数量；
• \(c_{ij}\)：表示单位货物从产地 \(i\) 运至销地 \(j\) 的运输成本；
• \(a_i\)：第 \(i\) 个产地的供给量；
• \(b_j\)：第 \(j\) 个销地的需求量。

1.1 模型的矩阵形式

上式可用矩阵表达为：

\[\min Z = C^T X \]

\[\text{s.t.} \quad A X = b, \quad X \ge 0 \]

其中矩阵 \(A\) 是运输约束矩阵，也就是矩阵形式的系数矩阵，维度为 \((m+n) \times (mn)\)，其结构由两部分组成：

• 前 \(m\) 行表示每个产地的供给约束；
• 后 \(n\) 行表示每个销地的需求约束。

矩阵 \(A\) 的典型形式为：

\[A = \begin{bmatrix} 1 & 1 & \cdots & 1 & 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 & 1 & 1 & \cdots & 1 \\ \vdots & & \ddots & & & & \ddots & \\ 1 & 0 & \cdots & 0 & 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 & 0 & 1 & \cdots & 0 \\ \vdots & & & & & & \ddots & \end{bmatrix} \]

该矩阵具有显著的稀疏性和特殊线性结构，每一列仅在两个位置上取值为 1（一个属于产地约束，一个属于销地约束）。

!!!提醒注意：

• 决策变量有2个下标，第1个下标表示产地，第2个下标表示销地，这两个下标恰好刻画了物流运动的方向；
• 决策变量排序时优先考虑第1个下标，第1个下标相同时再排第2个下标，不然系数矩阵的特点不同；
• 所有约束都是等式，表面总产量没有剩余，总销量都得到满足，产销完美匹配。

1.2 模型特点分析

（1）平衡性条件

模型的核心条件为：

\[\sum_{i=1}^{m} a_i = \sum_{j=1}^{n} b_j \]

它保证供给端与需求端在总量上完全匹配，从而形成封闭系统。此条件使得问题存在可行解，否则必须引入虚拟点以实现平衡。

（2）线性约束结构清晰

每个产地约束对应一条线性方程：

\[\sum_{j=1}^{n} x_{ij} = a_i \]

每个销地约束对应一条线性方程：

\[\sum_{i=1}^{m} x_{ij} = b_j \]

因此整个系统共有 \(m + n\) 条线性约束，但由于总体平衡关系：

\[\sum_{i=1}^{m} a_i = \sum_{j=1}^{n} b_j \]

使得这 \(m + n\) 条方程中存在一条线性依赖关系，导致约束矩阵 \(A\) 的秩为：

\[\text{rank}(A) = m + n - 1 \]

即系统存在一个冗余约束。

（3）变量数量与约束数量的关系

模型的决策变量共有 \(m \times n\) 个，而独立约束方程数为 \(m + n - 1\)，因此在最优解中，基本变量数等于约束独立数。
换言之，在最优基可行解中，恰有 \(m + n - 1\) 个变量为正，其余变量为零，这也是运输问题“基变量数 = 约束独立数”的结构特征。

（4）目标函数的经济意义

目标函数：

\[Z = \sum_{i=1}^{m} \sum_{j=1}^{n} c_{ij} x_{ij} \]

表示系统的总运输成本。在约束条件下对其进行最小化，体现了运筹优化思想中的“成本最优配置”原则。由于模型线性，最优解通常位于可行域的顶点，便于使用单纯形法或运输算法求解。

（5）模型的稀疏性与求解效率

矩阵 \(A\) 的每一列仅包含两个非零元素，因此整个约束系统极为稀疏。
这种结构使得专门的 运输算法（Transportation Algorithm） 比通用线性规划算法更高效，例如：

• 西北角法（North-West Corner Method）：用于构造初始可行解；
• 最小元素法（Least Cost Method） 与 Vogel 近似法（VAM）：用于改进初始解；
• 位势法（Potential Method）：用于检验并优化解的最优性。

（6）模型的可扩展性

平衡型运输问题可自然扩展至：

• 多阶段运输问题（如仓储中转点模型）；
• 指派问题（当 \(a_i = b_j = 1\) 时）；
• 网络流模型（运输问题的特殊形式）。

1.3 汇总表

统一数学结构使得运输模型成为网络优化与线性规划研究的基础模型之一，见下表。

序号	特点名称	数学或结构说明	经济与方法论含义
1	供需平衡性	满足总供给等于总需求：\(\sum_{i=1}^{m} a_i = \sum_{j=1}^{n} b_j\)	保证模型可行且系统封闭，是平衡型模型的核心特征
2	线性与稀疏性	约束系数矩阵 \(A\) 为稀疏矩阵，每列仅含两个非零元素	结构清晰、计算效率高，便于线性规划算法实现
3	秩为 \(m+n-1\)	\(A\) 的 \(m+n\) 个约束中存在一条线性相关方程	系统存在一个冗余约束，决定基本变量数为 \(m+n-1\)
4	经济含义明确	目标函数 \(Z=\sum c_{ij}x_{ij}\) 表示总运输成本	模型体现成本最小化原理，具有直观的经济解释
5	求解高效性	可用运输算法、位势法、Vogel法等特化算法	计算复杂度低于通用单纯形法，适用于大规模问题
6	扩展性强	可扩展至多阶段运输、指派与网络流模型	模型结构稳定，可广泛应用于物流与资源配置领域

平衡型运输问题因其结构优美、经济意义清晰、计算效率高，而成为线性规划理论与实际优化应用中的重要典型模型。

---

二、系数矩阵秩\(m+n-1\)的推导

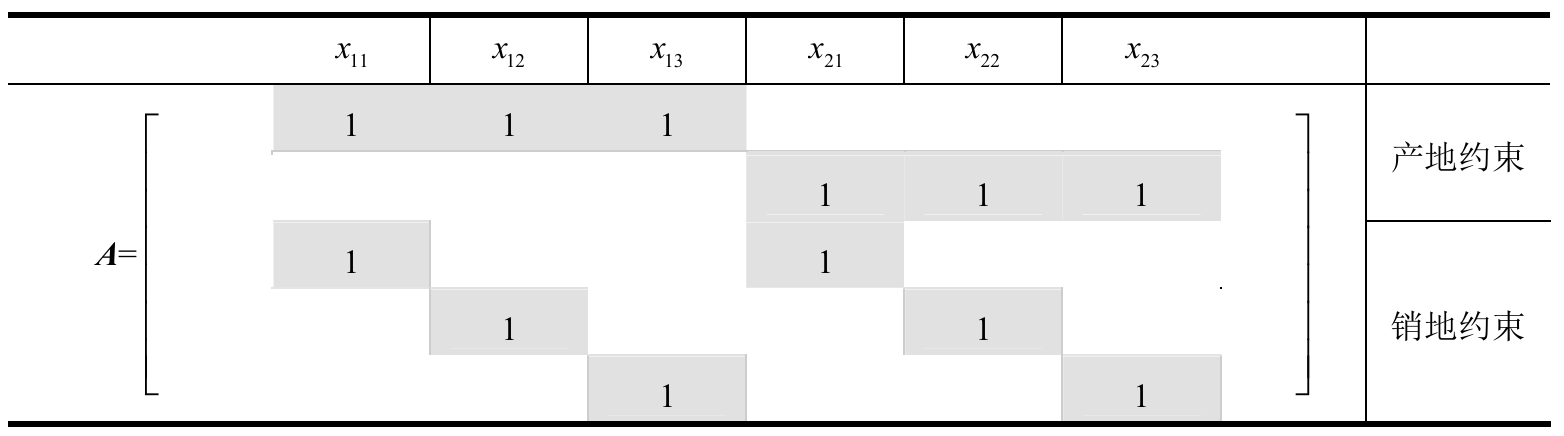
设运输问题的约束矩阵为：

\[A = \begin{bmatrix} 1 & 1 & 1 & 0 & 0 & 0 \\[6pt] 0 & 0 & 0 & 1 & 1 & 1 \\[6pt] 1 & 0 & 0 & 1 & 0 & 0 \\[6pt] 0 & 1 & 0 & 0 & 1 & 0 \\[6pt] 0 & 0 & 1 & 0 & 0 & 1 \end{bmatrix} \]

其中列向量依次对应变量：

\[(x_{11}, x_{12}, x_{13}, x_{21}, x_{22}, x_{23}) \]

行向量对应五条约束：

• 前两行为 产地约束；
• 后三行为 销地约束。

---

2.1 约束关系分析

产销平衡条件下，两个产地约束的和等于三个销地约束的和，即：

\[(x_{11}+x_{12}+x_{13}) + (x_{21}+x_{22}+x_{23}) = (x_{11}+x_{21}) + (x_{12}+x_{22}) + (x_{13}+x_{23}) \]

因此五条约束中存在一条线性相关关系。
也就是说，五个约束中有一个是冗余约束，矩阵 \(A\) 的秩不可能达到 5。

2.2 子矩阵 \(A_{(1,4,5,6)}\) 的秩分析

从矩阵 \(A\) 中取出第 1、4、5、6 列，得到子矩阵：

\[A_{(1,4,5,6)} = \begin{bmatrix} 1 & 0 & 0 & 0 \\[6pt] 0 & 1 & 1 & 1 \\[6pt] 1 & 1 & 0 & 0 \\[6pt] 0 & 0 & 1 & 0 \\[6pt] 0 & 0 & 0 & 1 \end{bmatrix} \]

对该子矩阵进行行变换可以验证，其中 4 行线性无关，因此：

\[\text{rank}(A_{(1,4,5,6)}) \ge 4 \]

2.3 结论

由于整个矩阵 \(A\) 的秩不超过 4（存在一条约束冗余），
而其子矩阵 \(A_{(1,4,5,6)}\) 的秩至少为 4，
因此可以确定：

\[\boxed{\text{rank}(A) = 4} \]

2.4 推广结论

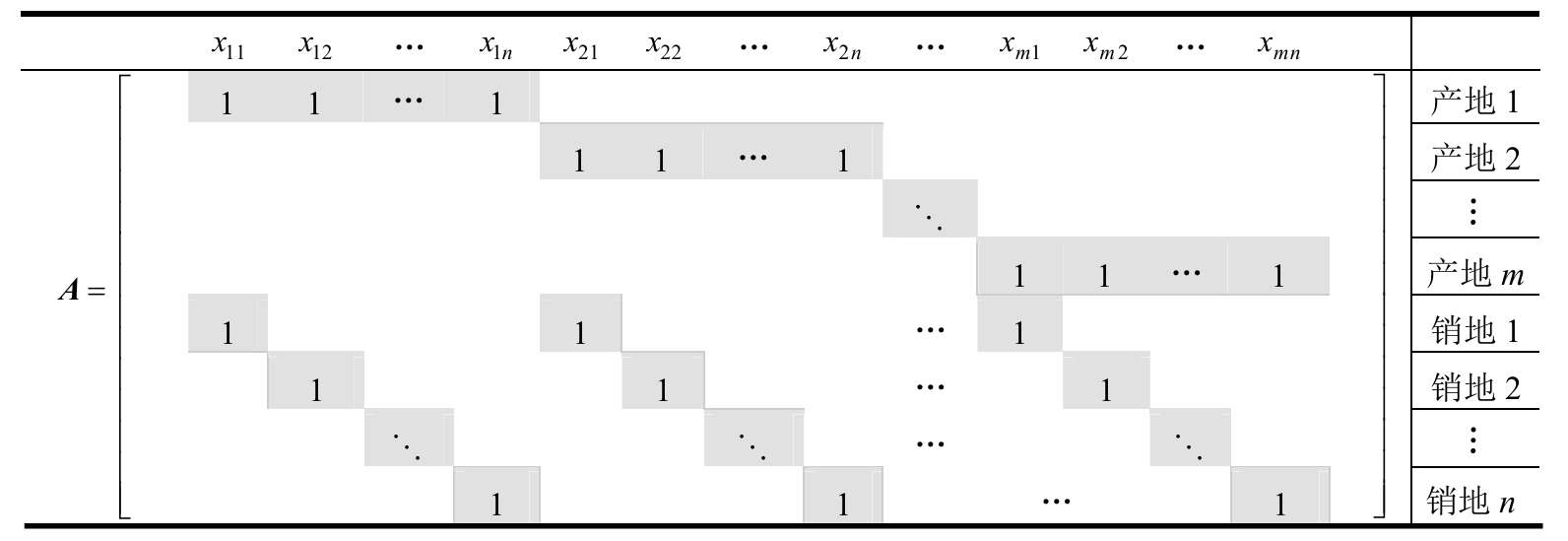
对于一般的 \(m\) 个产地与 \(n\) 个销地的运输问题，
约束矩阵 \(A\) 的秩满足：

\[\text{rank}(A) = m + n - 1 \]

例中 \(m=2, n=3\)，故有：

\[\text{rank}(A) = 2 + 3 - 1 = 4 \]

三、平衡型运输问题基可行解的变量个数

在线性规划的基本理论中，若模型有 n 个变量与 r 个线性无关约束方程，则任意一个基本解（basic solution）由 恰好 r 个基变量（basic variables） 决定，其余 n - r 个变量称为非基变量（non-basic variables），并被置为零。由此可知，一个基本解对应于从 n 个变量中选取 r 个构成的基矩阵 B，并满足：

\[x_B = B^{-1}b,\quad x_N = 0 \]

3.1 基可行解的变量个数为\(m+n-1\)

对于运输问题，由于独立约束的数量为：

\[r = m + n - 1 \]

因此每一个非退化的基可行解（Basic Feasible Solution, BFS）应当恰好有：$$m + n - 1$$个变量为正（即基变量），其余：

\[mn - (m + n - 1) = (m - 1)(n - 1) \]

个变量为零。

若 m = 2, n = 3，则共有：$$mn = 6$$个变量：

\[x_{11}, x_{12}, x_{13}, x_{21}, x_{22}, x_{23} \]

共有 m + n = 5 个约束方程，但独立方程数为：

\[r = 2 + 3 - 1 = 4 \]

因此，一个基可行解中必须恰好有 4 个变量为正（基变量），其余 2 个为零。

3.2 \(m+n-1\)变量构成一个基的条件

在线性代数的框架下，可以诠释“不构成闭回路的 $ m+n-1 $ 个变量是一个基”。其核心在于：运输问题的约束方程系统本质上是一个具有特定结构的线性方程组，而“基”的定义就是指能够形成线性无关列向量组的变量集合。

运输问题的标准形式可以写成矩阵形式

\[A x = b, \quad x \ge 0, \]

其中 $ A $ 是运输问题的约束系数矩阵，维度为 \((m+n) \times (mn)\)。矩阵 $ A $ 具有如下结构特征：
每个变量 $ x_{ij} $ 在第 $ i $ 行（供给约束）和第 $ m+j $ 行（需求约束）各出现一次，其余元素为零。由于所有供给与需求约束之和恒等（\(\sum_i a_i = \sum_j b_j\)），矩阵 $ A $ 的秩为

\[\text{rank}(A) = m + n - 1. \]

因此，系统 $ A x = b $ 中任意一组线性无关列的最大个数只能是 $ m + n - 1 $。若选取了 $ r = m + n - 1 $ 个变量，使得对应的列向量线性无关，则这些变量可以唯一确定一个基本解；若再加入任意一个变量，其列向量必为这 $ r $ 个列的线性组合，从而引入线性相关性。

“闭回路”在代数上正对应这种线性相关关系。若选取的变量集合在代数意义上形成一组相关列，则必然存在一组非零系数 $ \lambda_{ij} $，使得

\[\sum_{(i,j)\in S} \lambda_{ij} A_{(i,j)} = 0, \]

其中 $ S $ 是所选变量的索引集合。由于每个 $ A_{(i,j)} $ 含两个 1（分别在第 $ i $ 行和第 $ m+j $ 行），线性相关意味着在供需节点之间存在一组系数互相抵消的循环关系——这正是图论意义上的“闭回路”。反之，若不存在此类线性相关组合，即列向量独立，则相应变量集合不形成闭回路，从而构成一个基。

因此，运输问题中“不构成闭回路的 $ m+n-1 $ 个变量”意味着选取了恰好秩数目的线性无关列向量，它们张成约束空间并可唯一解出对应变量，构成一个线性无关的基变量集，这正是运输问题基本可行解的本质。

---

总结

平衡型运输问题作为运输模型的核心形式，体现了线性规划中供需均衡与成本最优化的思想。其基本条件是总供给量等于总需求量，使系统形成封闭平衡结构。该模型以最小化运输总成本为目标，约束矩阵稀疏且秩为 \(m + n - 1\)，说明其中存在一条冗余方程。由于结构线性、变量与约束间关系清晰，平衡型运输问题不仅在理论上具有简洁的数学形式，而且在实际中计算效率高、可解释性强。它广泛应用于物流配送、生产计划、能源调度等领域，是研究资源优化配置与网络流模型的重要基础。