计量经济学(十九)——广义线性模型GLM

广义线性模型（Generalized Linear Model，GLM）是一种灵活且强大的回归分析方法，它将传统线性回归模型与其他类型的回归模型整合集成在一起，其核心逻辑就是利用指数族分布的结构，把非线性的响应变量均值问题转化为一个线性预测问题。GLM 通过指定不同的链接函数和分布族，可以适应多种数据类型。它不仅适用于常见的正态分布数据，还能够处理泊松分布、二项分布、伽马分布等，适用于计数数据、分类数据和连续数据等。通过选择合适的链接函数（如 log、logit、identity 等）和分布（如泊松分布用于计数数据，二项分布用于分类问题），GLM 能够为多种回归问题提供统一框架，且兼容传统回归分析方法。

目录

一、 引言
二、 广义线性模型（GLM）的基本理论
三、 GLM的估计方法
四、 GLM的诊断
五、 GLM的应用案例
六、 GLM的Python实现
七、 结束语
八、 参考文献

一、引言

回归分析在计量经济学中占据着核心地位，广泛应用于揭示经济变量之间的关系。在多元回归模型的框架下，研究者通过自变量预测因变量。然而，传统的回归模型（如线性回归）假设因变量符合正态分布，且与自变量之间存在线性关系，限制了其应用范围。在实际经济问题中，许多情境下因变量并不符合正态分布，且自变量和因变量之间的关系可能是非线性的，这使得传统的回归方法无法提供令人满意的结果。为了解决这些问题，广义线性模型（GLM）应运而生。
GLM通过引入链接函数和适应不同的分布族，扩展了传统回归模型的应用范围，能够处理如二分类、计数数据、偏态数据等多种复杂情况。本文将详细探讨GLM的理论基础、主要类型、估计方法、模型诊断以及实际应用，帮助读者全面理解GLM的内涵及其在计量经济学中的重要地位。

二、广义线性模型（GLM）的基本理论

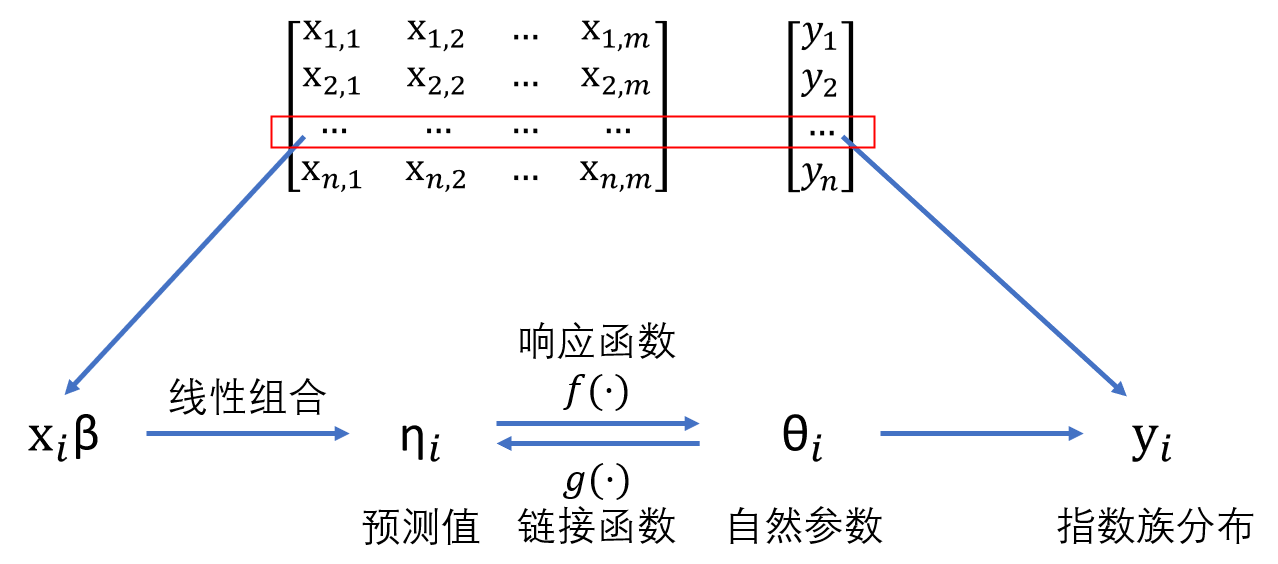
线性回归的核心思想是响应变量的条件均值可由自变量的线性组合直接刻画，即\(E[Y \mid X ] = X \beta\)。广义线性模型（GLM）在此基础上推广，引入链接函数 \(g (.)\)，使得\(g (E[ Y \mid X ]) = X \beta\)。通过这种方式，即使响应变量服从二项分布、泊松分布等非正态分布，也能将均值与线性预测子联系起来。其底层逻辑是依托于指数族分布，保证了响应变量的均值与自然参数之间存在可逆函数关系，而线性预测子 \(X \beta\) 则为建模提供了稳定而统一的框架。
广义线性模型（GLM）是一类灵活的回归模型，它通过引入不同的概率分布和链接函数，适应了多种类型的响应变量，克服了传统回归模型的局限性。GLM的框架由三部分组成：随机成分、系统成分和链接函数。广义线性模型的数学表示为：

\[g(\mu) = \eta = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p \]

其中：

  • $ \mu = E(Y)$ 是响应变量\(Y\) 的期望值。
  • \(g(\mu)\) 是链接函数。
  • \(\eta = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p\)是系统成分，即自变量与回归系数的线性组合。

这个公式展示了如何通过链接函数 $ g(\mu)$将响应变量的期望值与自变量之间的线性关系连接起来。下面将详细介绍这三个成分：随机成分、系统成分和链接函数。

2.1 随机成分（Random Component）

随机成分描述了响应变量的分布情况。在GLM中，响应变量 \(Y\) 通常假设服从某个指数分布族（如正态分布、二项分布、泊松分布等）。这些分布族描述了响应变量如何受到随机因素的影响，并影响其分布形式。具体来说，响应变量 \(Y\) 的概率密度函数可以表示为：

\[f_Y(y|\theta) = \exp \left( \frac{y\theta - b(\theta)}{\phi} + c(y, \phi) \right) \]

其中：

  • \(\theta\) 是分布的自然参数。
  • $ b(\theta)$ 和 $ c(y, \phi)$ 是由具体分布形式决定的函数。
  • \(\phi\) 是尺度参数。

常见的分布族包括：

  • 正态分布：用于处理连续数据，如股市价格、收入等。
  • 二项分布：用于处理二分类数据，如是否患病、是否购买某产品等。
  • 泊松分布：用于处理计数数据，如事故发生次数、客户到店数量等。
  • Gamma分布：常用于处理正偏态数据，如保险赔付金额、排队时间等。

2.2 系统成分（Systematic Component）

系统成分描述了自变量与响应变量之间的线性关系。这个部分由自变量和回归系数组成，通常表示为：

\[\eta = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p \]

其中：

  • $ \eta $ 是线性预测量（即自变量的加权和）。
  • \(X_1, X_2, \dots, X_p\) 是自变量。
  • \(\beta_0, \beta_1, \dots, \beta_p\) 是回归系数。

系统成分通常用于建立自变量与响应变量之间的线性关系，但需要通过链接函数与响应变量的期望值（\(\mu\)）建立联系。

链接函数将系统成分（线性预测量）与响应变量的期望值 \(\mu = E(Y)\) 联系起来。不同类型的响应变量需要不同的链接函数。链接函数的作用是将响应变量的期望值与自变量的线性组合进行非线性变换，常见的链接函数包括：

  • 对数链接函数（用于泊松回归、Gamma回归等）：\(g(\mu) = \log(\mu)\)
  • 逻辑斯蒂链接函数（用于逻辑回归）：\(g(\mu) = \log \left( \frac{\mu}{1 - \mu} \right)\)
  • 恒等链接函数（用于线性回归）：$g(\mu) = \mu $

通过这些链接函数，GLM能够处理自变量与响应变量之间的非线性关系，从而适应更多复杂的回归问题。

2.4 GLM的常见特例

广义线性模型（GLM）是一个通用框架，可以根据响应变量的类型和分布选择不同的特例。下面列举十种常见的GLM特例：

模型类型 响应变量分布 链接函数 应用场景
多元线性回归（Multiple Linear Regression） 正态分布 恒等函数 \(g(\mu) = \mu\) 预测连续型经济指标，如收入、GDP、股价等
逻辑回归（Logistic Regression） 二项分布 逻辑斯蒂函数 \(g(\mu) = \log\frac{\mu}{1-\mu}\) 二分类问题，如信用违约预测、患病概率预测
泊松回归（Poisson Regression） 泊松分布 对数函数 \(g(\mu) = \log(\mu)\) 计数数据分析，如事故次数、客户到店次数
负二项回归（Negative Binomial Regression） 负二项分布 对数函数\(g(\mu) = \log(\mu)\) 过度离散的计数数据，如保险理赔次数、疾病发病次数
Gamma回归（Gamma Regression） Gamma分布 对数函数\(g(\mu) = \log(\mu)\) 处理正偏态连续数据，如保险赔付金额、排队时间
多项Logit回归（Multinomial Logistic Regression） 多项分布 对数几率函数 \(g(\mu_i) = \log\frac{\mu_i}{\mu_J}\) 多分类问题，如消费者购买品牌选择、投票意向预测
Ordinal Logit回归（Ordinal Logistic Regression） 有序多项分布 对数几率函数 \(g(\mu_i) = \log\frac{P(Y \le i)}{P(Y > i)}\) 有序分类问题，如满意度评分（差、中、好）
Probit回归（Probit Regression） 二项分布 普通正态函数 \(g(\mu) = \Phi^{-1}(\mu)\) 二分类问题，类似逻辑回归，常用于金融、医学等领域
Beta回归（Beta Regression） Beta分布 对数it函数 \(g(\mu) = \log\frac{\mu}{1-\mu}\) 处理比例数据，如市场份额、转化率、占比数据
Quasi-Poisson回归（Quasi-Poisson Regression） 近似泊松分布 对数函数\(g(\mu) = \log(\mu)\) 处理过度离散计数数据，但不严格假设泊松分布

上述结构展示了GLM的通用数学表达式，依次解释了三个组成部分——随机成分、系统成分和链接函数，并给出了每一部分的具体数学表达和应用场景。这使得读者可以更好地理解广义线性模型的构建和应用。

泊松分布与 GLM

  • 分布形式：

    \[P(Y=y) = \frac{e^{-\mu}\mu^y}{y!}, \quad y=0,1,2,\dots \]

  • 指数族改写：

    \[P(Y=y) = \exp\left(y \log \mu - \mu - \log y!\right) \]

    可得自然参数 \(\theta = \log \mu\)。
  • 均值关系：

\[\mathbb{E}[Y] = e^{\theta} = \mu \]

  • GLM 表达：

\[\log \mu = X\beta \quad \Rightarrow \quad \mu = e^{X\beta} \]

泊松分布属于指数族，GLM 使用 对数链接函数 将均值建模为自变量的线性函数。

三、GLM的估计方法

广义线性模型（GLM）的核心任务是估计回归系数 \(\beta = (\beta_0, \beta_1, \dots, \beta_p)^\top\)，从而刻画自变量与响应变量之间的关系。与传统线性回归不同，GLM允许响应变量服从非正态分布，这使得最小二乘法不再适用。因此，GLM的参数估计通常依赖于最大似然估计（MLE），结合数值优化方法如迭代加权最小二乘法（IWLS）来实现。

3.1 最大似然估计（MLE）

最大似然估计是一种通用且有效的参数估计方法，其核心思想是选择一组参数，使得在该参数下观测数据出现的概率（即似然函数）最大。对于GLM，假设响应变量 \(Y_i\) 独立且服从指数分布族，其概率密度函数可表示为：

\[f_Y(y_i|\theta_i) = \exp \left( \frac{y_i \theta_i - b(\theta_i)}{\phi} + c(y_i, \phi) \right) \]

其中，\(\theta_i\) 是自然参数，\(\phi\) 是尺度参数。最大化似然函数 \(L(\beta) = \prod_{i=1}^n f_Y(y_i|\theta_i(\beta))\) 等价于最大化对数似然函数：

\[\ell(\beta) = \sum_{i=1}^n \frac{y_i \theta_i - b(\theta_i)}{\phi} + \sum_{i=1}^n c(y_i, \phi) \]

通过对 \(\beta\) 求导并令其导数为零，可以得到最大似然方程。然而，由于许多GLM模型的对数似然方程是非线性的，解析解往往不存在，因此需要数值迭代方法求解。

3.2 迭代加权最小二乘法（IWLS）

迭代加权最小二乘法（IWLS）是GLM中求解最大似然估计的标准算法。其基本思想是将非线性的最大似然估计问题转化为一系列加权最小二乘问题，通过不断迭代更新回归系数，直到收敛。具体步骤如下：

  • 初始化回归系数 \(\beta^{(0)}\)。
  • 计算当前系数下的线性预测量 \(\eta^{(t)} = X \beta^{(t)}\) 及响应变量的期望值 \(\mu^{(t)} = g^{-1}(\eta^{(t)})\)。
  • 构造权重矩阵 \(W^{(t)}\) 和调整响应变量的伪响应 \(z^{(t)}\)：

    \[z^{(t)} = \eta^{(t)} + (y - \mu^{(t)}) \left( \frac{d\eta}{d\mu} \right)_{\mu^{(t)}} \]

  • 求解加权最小二乘方程：

    \[\beta^{(t+1)} = (X^\top W^{(t)} X)^{-1} X^\top W^{(t)} z^{(t)} \]

  • 重复步骤2-4，直到 \(\beta\) 收敛（变化量小于设定阈值）。

IWLS方法能够高效处理各种分布族和链接函数，使得GLM的参数估计过程在理论上严谨且在计算上可行。通过MLE与IWLS，研究者可以在不同类型的数据下得到稳健的回归系数，从而对经济变量之间的关系进行有效建模与推断。|

四、GLM的诊断

在广义线性模型（GLM）建模过程中，诊断分析是确保模型有效性和稳健性的重要环节。由于GLM允许响应变量服从非正态分布，模型可能存在拟合不足、异常值或系统性偏差，因此对残差、拟合优度和偏差进行检查，有助于发现潜在问题并优化模型结构。

4.1 残差分析

残差分析用于检查模型拟合效果和数据的异常情况。在GLM中，常用残差类型包括偏差残差（deviance residuals）、皮尔逊残差（Pearson residuals）和工作残差（working residuals）。偏差残差定义为：

\[r_i^{(D)} = \text{sign}(y_i - \hat{\mu}_i) \sqrt{2 \left[ \ell(y_i; y_i) - \ell(\hat{\mu}_i; y_i) \right]} \]

其中，\(\ell(\cdot)\)为对数似然函数，\(\hat{\mu}_i\)为模型预测值。通过绘制残差与拟合值的散点图，可以发现异常值、非线性趋势或异方差问题，从而判断模型是否需要调整或引入其他变量。

4.2 拟合优度检验

拟合优度检验用于评估模型解释响应变量的能力。常用的方法包括：

  • 卡方检验（Chi-square test）：对比模型残差与理论分布，判断模型是否合理。
  • 赤池信息准则（AIC, Akaike Information Criterion）：

\[\text{AIC} = -2 \ell(\hat{\beta}) + 2 k \]

其中，\(\ell(\hat{\beta})\)是对数似然值，\(k\)是模型参数个数。AIC值越小，模型拟合越优。

  • 贝叶斯信息准则（BIC, Bayesian Information Criterion）：

\[\text{BIC} = -2 \ell(\hat{\beta}) + k \log(n) \]

BIC在模型选择中考虑了样本量，适用于比较不同复杂度的模型。

这些指标可以帮助研究者在多个候选模型中选择最优模型，并避免过拟合。

4.3 偏差诊断

偏差诊断用于检查模型是否存在系统性误差，即模型假设与数据实际分布的偏离情况。常用方法包括偏差残差图和偏差分布图。通过分析残差分布是否接近零均值及是否存在规律性偏差，可以判断模型是否遗漏重要变量或选择了不合适的链接函数。如果发现明显模式，则可能需要重新定义自变量或选择更合适的分布族。

综合来看，GLM的诊断环节对于保证模型的稳健性和预测能力至关重要。通过残差分析、拟合优度检验和偏差诊断，研究者不仅可以发现异常数据和潜在问题，还能够进一步优化模型结构，提高对经济、金融及社会科学数据的解释力和预测精度。

五、GLM的应用案例

广义线性模型（GLM）因其灵活性和适用性，在各行各业的数据分析中都有广泛应用。它不仅可以处理连续型响应变量，还能对二分类、多分类以及计数型数据进行建模，因此在医疗、金融和社会科学等领域都表现出重要价值。

5.1 医疗数据分析

在医疗领域，GLM被广泛应用于疾病预测、风险评估和医疗资源规划。举例来说，逻辑回归可用于预测患者是否患有某种慢性疾病，如糖尿病或心血管疾病。研究者可以将年龄、性别、血压、血糖水平、生活习惯等作为自变量，构建逻辑回归模型，从而估计每位患者的患病概率。此外，泊松回归则常用于预测患者的住院次数或急诊就诊次数。通过将患者的历史就诊记录、病情严重程度和治疗方案作为自变量，泊松回归能够合理地模拟计数型响应变量，为医院资源配置提供决策依据。GLM在医疗数据分析中不仅能够提高预测精度，还能帮助识别重要的风险因素，为公共卫生政策制定提供科学依据。

5.2 金融数据分析

在金融领域，GLM同样有着广泛应用，尤其在信用风险管理和保险精算中发挥重要作用。例如，泊松回归可以用来预测保险理赔的次数，通过分析客户的年龄、性别、职业、投保类型和历史理赔记录，模型可以为保险公司提供合理的赔付预测。另一方面，逻辑回归则是信用评分模型的核心工具，用于预测客户是否会违约。通过将客户的收入水平、信用历史、负债比率等作为自变量，逻辑回归能够估计违约概率，为信贷审批和风险控制提供数据支持。GLM在金融数据分析中，能够处理二分类与计数型问题，使金融机构在风险管理和精算定价方面更加科学和精准。

5.3 社会科学研究

在社会科学领域，GLM被广泛用于教育、社会行为、政治投票及公共政策研究。例如，逻辑回归可以用于分析选民是否会支持某一政策或候选人，将性别、年龄、收入水平、教育背景等因素作为自变量，预测选民行为概率。泊松回归则可用于研究事件发生频率，如青少年犯罪率、参与志愿活动的次数等。GLM的应用不仅可以帮助研究人员理解社会现象背后的因果关系，还可以通过模型解释变量的重要性，为政策制定和社会干预提供量化依据。此外，GLM能够适应不同类型的响应变量，使得社会科学研究者能够处理从连续到计数、从二分类到多分类的多样化数据问题。

广义线性模型在各个领域都体现出强大的建模能力和实用价值，通过选择合适的分布和链接函数，研究人员和决策者能够针对不同数据类型进行科学建模，实现对复杂现实问题的精准分析和预测。

六、GLM的Python实现

6.1 广义线性模型的拟合函数

Python中sm.GLM() 方法来拟合不同类型的广义线性模型，并且指明了每个模型对应的 family 和 link。

模型类型 GLM 用法示例 family 设置 link 函数设置 备注
多元线性回归（Multiple Linear Regression） sm.GLM(y, X, family=sm.families.Gaussian(), link=sm.families.links.identity()) Gaussian 恒等函数（identity） 适用于连续型响应变量，预测经济指标等
逻辑回归（Logistic Regression） sm.GLM(y, X, family=sm.families.Binomial(), link=sm.families.links.logit()) Binomial 逻辑斯蒂函数（logit） 用于二分类问题，如信用违约预测、患病概率预测等
泊松回归（Poisson Regression） sm.GLM(y, X, family=sm.families.Poisson(), link=sm.families.links.log()) Poisson 对数函数（log） 适用于计数数据分析，如事故次数、客户到店次数等
负二项回归（Negative Binomial Regression） sm.GLM(y, X, family=sm.families.NegativeBinomial(), link=sm.families.links.log()) NegativeBinomial 对数函数（log） 适用于过度离散的计数数据，如保险理赔次数、疾病发病次数等
Gamma回归（Gamma Regression） sm.GLM(y, X, family=sm.families.Gamma(), link=sm.families.links.log()) Gamma 对数函数（log） 适用于处理正偏态连续数据，如保险赔付金额、排队时间等
多项Logit回归（Multinomial Logistic Regression） sm.GLM(y, X, family=sm.families.Multinomial(), link=sm.families.links.logit()) Multinomial 对数几率函数（logit） 适用于多分类问题，如消费者购买品牌选择、投票意向预测等
Ordinal Logit回归（Ordinal Logistic Regression） sm.GLM(y, X, family=sm.families.Binomial(), link=sm.families.links.logit()) Ordinal（可选） 对数几率函数（logit） 用于有序分类问题，如满意度评分、等级评分等
Probit回归（Probit Regression） sm.GLM(y, X, family=sm.families.Binomial(), link=sm.families.links.probit()) Binomial 普通正态函数（probit） 适用于二分类问题，通常与Logit回归进行比较
Beta回归（Beta Regression） sm.GLM(y, X, family=sm.families.Beta(), link=sm.families.links.logit()) Beta 对数it函数（logit） 处理比例数据，如市场份额、转化率、占比数据等
Quasi-Poisson回归（Quasi-Poisson Regression） sm.GLM(y, X, family=sm.families.Poisson(), link=sm.families.links.log()) Poisson 对数函数（log） 用于过度离散计数数据，但不严格假设泊松分布

说明：

  • family：指定响应变量的分布类型。
  • link：指定链接函数，它定义了响应变量与线性预测器之间的关系。例如，Logit 函数是针对二分类的逻辑回归，Log 函数是泊松回归、负二项回归、Gamma回归的常用链接函数。

6.2 Python程序

Seaborn 提供了一个内置的 penguins 数据集，用于分析不同企鹅物种的特征与分布。该数据集包含多个生物学特征，如 bill_length_mm（喙长）、bill_depth_mm（喙深）、flipper_length_mm（鳍长）等，以及不同物种的标签。我们可以通过这些数据来建立回归模型，探索企鹅物种特征与其分布之间的关系，进而分析不同特征对物种分布的影响。

import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.genmod.families import Poisson
from statsmodels.genmod.families.links import log
import seaborn as sns
import matplotlib.pyplot as plt

# 加载 seaborn 自带的 'penguins' 数据集
data = sns.load_dataset('penguins')

# 查看数据
print(data.head())

# 过滤缺失数据
data_cleaned = data.dropna(subset=['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm', 'species'])

# 显示清洗后的数据
print(data_cleaned.head())

# 将品种 'species' 转换为分类变量，并转换为整数编码
data_cleaned['species_code'] = data_cleaned['species'].astype('category').cat.codes

# 定义自变量和因变量
X = data_cleaned[['bill_length_mm', 'bill_depth_mm', 'flipper_length_mm']]  # 多个自变量
X = sm.add_constant(X)  # 添加常数项
y = data_cleaned['species_code']  # 因变量：品种的编码（0, 1, 2）

# GLM建模：Poisson回归
poisson_model = sm.GLM(y, X, family=Poisson(), link=log())
poisson_results = poisson_model.fit()

# 输出回归结果
print(poisson_results.summary())

# 输出预测的品种编码
y_pred = poisson_results.predict(X)

# 可视化结果：通过散点图和预测值
plt.figure(figsize=(10, 6))

# 使用不同颜色展示预测和实际物种
sns.scatterplot(x=y, y=y_pred, color='blue', alpha=0.6)

# 添加标签和标题
plt.xlabel('True Species Code')
plt.ylabel('Predicted Species Code')
plt.title('True vs Predicted Species Code')

# 显示图表
plt.show()

# 可选：使用分类的色彩显示
sns.scatterplot(x=y, y=y_pred, hue=y, palette="deep", alpha=0.6)

# 再次设置标签和标题
plt.xlabel('True Species Code')
plt.ylabel('Predicted Species Code')
plt.title('True vs Predicted Species Code with Classification')
plt.legend(title='Species')
plt.show()

image

 species     island  bill_length_mm  ...  flipper_length_mm  body_mass_g     sex
0  Adelie  Torgersen            39.1  ...              181.0       3750.0    Male
1  Adelie  Torgersen            39.5  ...              186.0       3800.0  Female
2  Adelie  Torgersen            40.3  ...              195.0       3250.0  Female
3  Adelie  Torgersen             NaN  ...                NaN          NaN     NaN
4  Adelie  Torgersen            36.7  ...              193.0       3450.0  Female

                Generalized Linear Model Regression Results                  
==============================================================================
Dep. Variable:           species_code   No. Observations:                  342
Model:                            GLM   Df Residuals:                      338
Model Family:                 Poisson   Df Model:                            3
Link Function:                    Log   Scale:                          1.0000
Method:                          IRLS   Log-Likelihood:                -277.76
Date:                Sat, 06 Sep 2025   Deviance:                       98.035
Time:                        16:07:10   Pearson chi2:                     80.7
No. Iterations:                     5   Pseudo R-squ. (CS):             0.5799
Covariance Type:            nonrobust                                         
=====================================================================================
                        coef    std err          z      P>|z|      [0.025      0.975]
-------------------------------------------------------------------------------------
const                -2.6067      1.491     -1.748      0.080      -5.530       0.316
bill_length_mm        0.1349      0.018      7.606      0.000       0.100       0.170
bill_depth_mm        -0.3259      0.042     -7.797      0.000      -0.408      -0.244
flipper_length_mm     0.0079      0.007      1.168      0.243      -0.005       0.021
=====================================================================================

6.3 结果分析

这是通过 广义线性模型 (GLM) 使用泊松回归模型对企鹅物种分布进行分析的结果。模型使用 log 链接函数，目的是预测不同企鹅物种（用 species_code 表示）在不同生物学特征下的出现频率。

模型参数解读

  • 截距项 (const)：
    截距为 -2.6067，表示当所有自变量（如喙长、喙深、鳍长）均为 0 时，企鹅物种的出现频率的对数值。由于 p 值为 0.080（略大于 0.05），这表明截距项的统计显著性不强，但仍然接近于显著性水平。

  • bill_length_mm（喙长）：
    系数为 0.1349，表示喙长每增加 1 毫米，企鹅物种出现频率的对数值增加 0.1349。这个系数的 p 值为 0.000，远小于 0.05，表明喙长在模型中对物种分布有显著影响。

  • bill_depth_mm（喙深）：
    系数为 -0.3259，表示喙深每增加 1 毫米，企鹅物种出现频率的对数值减少 0.3259。p 值为 0.000，表明喙深对物种分布有显著负向影响。

  • flipper_length_mm（鳍长）：
    系数为 0.0079，表示鳍长每增加 1 毫米，企鹅物种出现频率的对数值增加 0.0079。p 值为 0.243，表明鳍长对物种分布的影响不显著。

模型评估

  • 对数似然值 (Log-Likelihood)：
    -277.76，表明模型拟合的好坏，较低的对数似然值通常意味着模型拟合不够好。
  • 偏差（Deviance）：
    98.035，偏差越小，模型的拟合越好。在泊松回归中，偏差可以用来衡量模型的拟合度，较低的偏差通常代表更好的模型拟合。
  • 皮尔逊卡方（Pearson chi2）：
    80.7，用于评估模型拟合的好坏，较低的卡方值表示模型的拟合较好。
  • 伪 R² (Pseudo R-squared)：
    伪 R² 值为 0.5799，表示模型解释了约 57.99% 的物种分布的变化，表明该模型具有较好的拟合效果。

显著性检验

  • 喙长 (bill_length_mm) 和 喙深 (bill_depth_mm) 都具有显著影响（p < 0.05），这两个变量与物种分布具有显著的正向和负向相关关系。
  • 鳍长 (flipper_length_mm) 的 p 值为 0.243，大于 0.05，表示鳍长在模型中的影响不显著。

最终模型

根据上述分析，最终的广义线性模型公式为：

log(species_code) = -2.6067 + 0.1349 * bill_length_mm - 0.3259 * bill_depth_mm} + 0.0079 * flipper_length_mm

其中：

  • species_code：企鹅物种的出现频率。
  • bill_length_mm：喙长（单位：毫米）。
  • bill_depth_mm：喙深（单位：毫米）。
  • flipper_length_mm：鳍长（单位：毫米）。

结论

  • 喙长和喙深对企鹅物种的分布有显著影响。喙长越长，物种出现频率越高；而喙深越大，物种出现频率越低。
  • 鳍长在该模型中对物种分布的影响不显著，因此可以考虑在进一步建模时去除该变量。
  • 该模型解释了约 57.99% 的企鹅物种分布变异，表现出较好的拟合度。

七、结束语

广义线性模型（GLM）作为多元线性回归的自然扩展，提供了一个统一而灵活的框架，使研究者能够处理各种类型的响应变量，包括连续、二分类、多分类及计数型数据。通过引入不同的概率分布和链接函数，GLM克服了传统线性回归在非正态数据、异方差或非线性关系下的局限性。本文从GLM的基本理论出发，详细介绍了随机成分、系统成分和链接函数的数学表达，并结合最大似然估计和迭代加权最小二乘法解释了参数估计方法。在应用层面，GLM在医疗、金融和社会科学等领域展现了重要价值，无论是疾病预测、信用评分，还是社会行为建模，都体现了其灵活性和高效性。未来，随着数据量和数据类型的不断增加，GLM及其扩展模型将在经济、社会和工程领域的决策分析中发挥更大的作用，成为计量经济学、金融学和社会科学数据分析的重要工具。

参考文献

  1. McCullagh, P., & Nelder, J. A. (1989). Generalized Linear Models. 2nd Edition. Chapman & Hall/CRC.
  2. Agresti, A. (2015). Foundations of Linear and Generalized Linear Models. 2nd Edition. Wiley.
  3. Dobson, A. J., & Barnett, A. (2018). An Introduction to Generalized Linear Models. 4th Edition. CRC Press.
  4. Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning. 2nd Edition. Springer.
  5. Cameron, A. C., & Trivedi, P. K. (2013). Regression Analysis of Count Data. 2nd Edition. Cambridge University Press.
posted @ 2025-09-06 16:24  郝hai  阅读(717)  评论(0)    收藏  举报