启发式算法里程碑：遗传算法的发展脉络与应用前沿

在现代优化与人工智能领域，启发式算法已成为解决复杂问题的重要工具。它们以近似最优为目标，通过模拟自然或社会现象进行搜索，其中最具代表性的便是遗传算法。自20世纪70年代由约翰·霍兰德提出以来，遗传算法不仅开创了进化计算的研究方向，也推动了元启发式方法的广泛应用。无论是旅行商问题（TSP）这样的经典组合优化，还是神经架构搜索（NAS）、自动机器学习（AutoML）等前沿任务，遗传算法都展现出强大的适应性与生命力。

“自然进化的法则，不仅塑造了生物世界，也启迪了人类智能。遗传算法用有限计算模拟无限演化，使复杂问题得以优雅求解。”

目录

一、引言

“自然选择不是最强者的生存，而是最适应环境者的生存。” ——达尔文

在优化与人工智能的发展历程中，启发式算法始终扮演着举足轻重的角色。这类算法通过模拟自然现象或人类行为来探索解空间，在面对高维、非线性、非凸、多峰等复杂优化问题时，能够突破传统解析方法与梯度法的局限，为工程与科学研究提供近似最优解。在众多启发式算法中，**遗传算法（Genetic Algorithm, GA）**因其源于生物进化论的独特机制而脱颖而出。
遗传算法由美国计算机科学家**约翰·霍兰德（John H. Holland）在20世纪70年代提出，首次将“自然选择—遗传—变异”框架系统化，并在其经典著作《Adaptation in Natural and Artificial Systems》中建立理论模型。这一突破奠定了进化计算（Evolutionary Computation）**研究的基础，也为后续蚁群算法、粒子群算法等元启发式方法提供了范式。
本文围绕启发式算法框架、遗传算法理论基础、发展演变、典型应用四大方面展开系统阐述，并重点剖析霍兰德的学术贡献。同时结合TSP案例与Python实现，展示遗传算法在现代智能优化中的应用价值与发展前景。

二、启发式算法概述与里程碑地位

2.1 启发式算法简述

启发式算法（Heuristic Algorithm）是一类基于经验规则、问题特征与启发信息的优化方法，其核心思想是通过适度牺牲精确性以换取可接受的求解效率。与依赖严格数学推导与梯度信息的传统优化方法不同，启发式算法通常不要求目标函数具备连续性、可导性等条件，因此能够广泛适用于非线性、非凸、多峰、多约束等复杂优化问题。

在应用实践中，启发式算法的优势主要体现在以下几个方面：

  • 鲁棒性强：面对不确定性和高维空间时，仍能找到较优解；
  • 适用范围广：可应用于组合优化、函数优化、调度问题、路径规划等多个领域；
  • 易于结合：常与局部搜索、数学规划或机器学习方法结合，形成混合优化框架。

常见启发式算法包括模拟退火算法（SA）、禁忌搜索算法（TS）、蚁群优化算法（ACO）、**粒子群优化算法（PSO）**等。这些算法虽各具特色，但均遵循“在搜索空间中利用启发信息高效逼近全局最优解”的共同原则。

2.2 遗传算法的里程碑意义

在启发式算法的发展史上，**遗传算法（Genetic Algorithm, GA）具有不可替代的里程碑地位。它不仅是进化计算（Evolutionary Computation）**的奠基之作，更是元启发式方法的重要起点。其意义主要体现在以下几个方面：

  • 开创进化计算研究方向
    遗传算法首次将达尔文自然选择与孟德尔遗传规律引入优化问题，通过种群编码、选择、交叉与变异等操作模拟生物进化。这种基于群体的搜索模式为后续的进化策略（ES）、遗传规划（GP）、差分进化（DE）等奠定了方法论基础。
  • 推动元启发式算法框架形成
    遗传算法提出了“群体搜索 + 随机性 + 适应度评估”的统一框架，这一思路被后续蚁群优化、粒子群优化等广泛继承和发展，形成**元启发式算法（Meta-Heuristics）**体系。
  • 跨学科影响深远
    遗传算法不仅在计算机科学、运筹学中得到应用，还影响了经济学（如博弈策略演化）、生物信息学（如基因序列比对）、工程优化（如结构设计、路径规划）等多个领域。尤其在现代深度学习时代，遗传算法与神经网络架构搜索、自动机器学习（AutoML）等前沿方向深度融合，展现了其长久生命力与适应性。

遗传算法不仅是一种算法，更是一种跨越学科的思想，为后续几十年的智能优化研究开辟了全新道路。

三、遗传算法产生与理论基础

3.1 背景与霍兰德贡献

20世纪60-70年代，计算机科学、控制论与心理学的交叉研究快速发展，复杂适应系统（Complex Adaptive Systems）成为学术界重要前沿议题。在此背景下，美国密歇根大学的计算机科学家**约翰·霍兰德（John H. Holland）**敏锐地意识到：生物进化中的遗传与自然选择机制，可能为解决复杂优化问题提供一种全新的计算范式。
霍兰德提出将基因编码、选择、交叉与变异抽象为算法操作，将候选解表示为二进制串或其他编码形式，模拟自然界群体进化过程的迭代优化。1975年，他在经典著作《Adaptation in Natural and Artificial Systems》中系统阐述了遗传算法的理论框架与适应性模型，为进化计算（Evolutionary Computation）的发展奠定了基础。霍兰德不仅给出算法流程，还通过数学工具解释算法收敛与优良模式保留的机制，使遗传算法从经验方法提升为理论化优化模型。

3.2 模式定理（Schema Theorem）

遗传算法的理论基石之一是模式定理（Schema Theorem）。该定理刻画了遗传操作如何在代际演化中保留并扩展优良模式，为解释算法全局搜索能力提供了重要数学依据。

模式定理形式化表达如下：

\[m \left(\right. H , t + 1 \left.\right) \geq m \left(\right. H , t \left.\right) \frac{f \left(\right. H \left.\right)}{\overset{ˉ}{f}} \left[\right. 1 - p_{c} \frac{d \left(\right. H \left.\right)}{l - 1} - o \left(\right. H \left.\right) p_{m} \left]\right. \]

其中：

  • \(m \left(\right. H , t \left.\right)\)：模式 \(H\) 在第 \(t\) 代中的个体数；
  • \(f \left(\right. H \left.\right)\)：模式 \(H\) 的平均适应度；
  • \(\overset{ˉ}{f}\)​：种群平均适应度；
  • \(p_{c}\)​、\(p_{m}\)​：交叉与变异概率；
  • \(d \left(\right. H \left.\right)\)：模式定义长度；
  • \(o \left(\right. H \left.\right)\)：模式阶数（固定位数）。

定理表明：适应度高、定义长度短、阶数低的模式将在迭代中以更高概率被保留并扩散。这解释了遗传算法如何通过选择与交叉机制保留优良基因片段，并在种群演化中逐渐逼近全局最优解。

3.3 适应度函数框架

在遗传算法中，**适应度函数（Fitness Function）**用于评价个体优劣，决定选择操作的概率。常见形式为：

\[f \left(\right. x \left.\right) = \frac{1}{1 + g \left(\right. x \left.\right)} \]

其中 \(g \left(\right. x \left.\right)\)表示原始目标函数值（如路径长度、能耗或成本）。当问题为最小化目标时，适应度值越大代表解越优；若为最大化目标，则可直接将目标函数值作为适应度。

适应度函数不仅影响算法收敛速度，还影响多样性维持。为避免早熟收敛，常采用线性标度、排序标度或共享适应度等方法调整适应度分布，使群体保持探索与开发的平衡。这一框架的灵活性，使遗传算法能适配多目标优化、约束优化等多种情境，为其跨学科应用提供理论支撑。

四、发展脉络：从起源到现代融合

4.1 1970s-1980s：探索期

20世纪70年代初，遗传算法作为一种全新的优化方法刚刚问世，主要处于理论探索与基础实验阶段。霍兰德提出了算法框架与模式定理，为研究者提供了数学解释。与此同时，De Jong开展了首批系统化实验研究，设计了一系列基准测试函数，用以验证遗传算法在函数优化与简单组合问题上的性能表现。这一时期，研究重点集中在编码策略（主要为二进制编码）、基本算子（选择、交叉、变异）的效果，以及算法收敛性分析。虽然应用场景较为有限，但为后续推广打下了坚实基础。

4.2 1990s：应用扩展期

进入90年代，遗传算法逐渐走出实验室，迈向工程与工业应用。David E. Goldberg出版《Genetic Algorithms in Search, Optimization, and Machine Learning》，系统化总结了GA方法与实践经验，推动其在工业优化、机器学习、控制工程中的普及。

该时期的重要进展包括：

  • 实数编码遗传算法的提出，使GA更适合连续优化问题；
  • **多目标遗传算法（MOGA）**兴起，开辟多目标优化新领域；
  • 适应度比例选择与锦标赛选择等机制改进，提高了算法稳定性。

同时，GA在调度优化、路径规划、神经网络权重训练等问题中展现出巨大潜力，成为跨学科应用的重要工具。

4.3 2000s：混合与改进期

21世纪初，遗传算法面临两个挑战：一是收敛速度较慢，二是易陷入局部最优。研究者提出混合遗传算法（Hybrid GA），结合局部搜索（如爬山法、模拟退火）提升精度与效率；同时，与禁忌搜索、粒子群优化等方法的融合，形成多元进化框架。
此外，分布式与并行遗传算法成为新趋势，借助多核CPU与分布式计算平台，GA可处理更大规模问题。该时期还涌现出自适应参数调节策略与精英保留策略，显著改善了算法的收敛性能和稳定性。

4.4 2010s-至今：深度学习融合期

近年来，遗传算法迎来与深度学习和强化学习的深度融合。通过演化搜索优化神经网络架构（NAS），遗传算法在自动机器学习（AutoML）中发挥关键作用；同时，**进化强化学习（Evolutionary RL）**框架借助GA优化策略网络，使其在连续控制与高维状态空间中表现优异。
另一前沿是量子遗传算法（Quantum GA），通过量子比特叠加与量子干涉实现搜索空间指数级扩展，为未来超大规模优化问题提供潜在突破口。总体而言，遗传算法正从传统的启发式优化工具演变为智能计算与多学科融合的重要支柱。

五、算法原理与核心机制

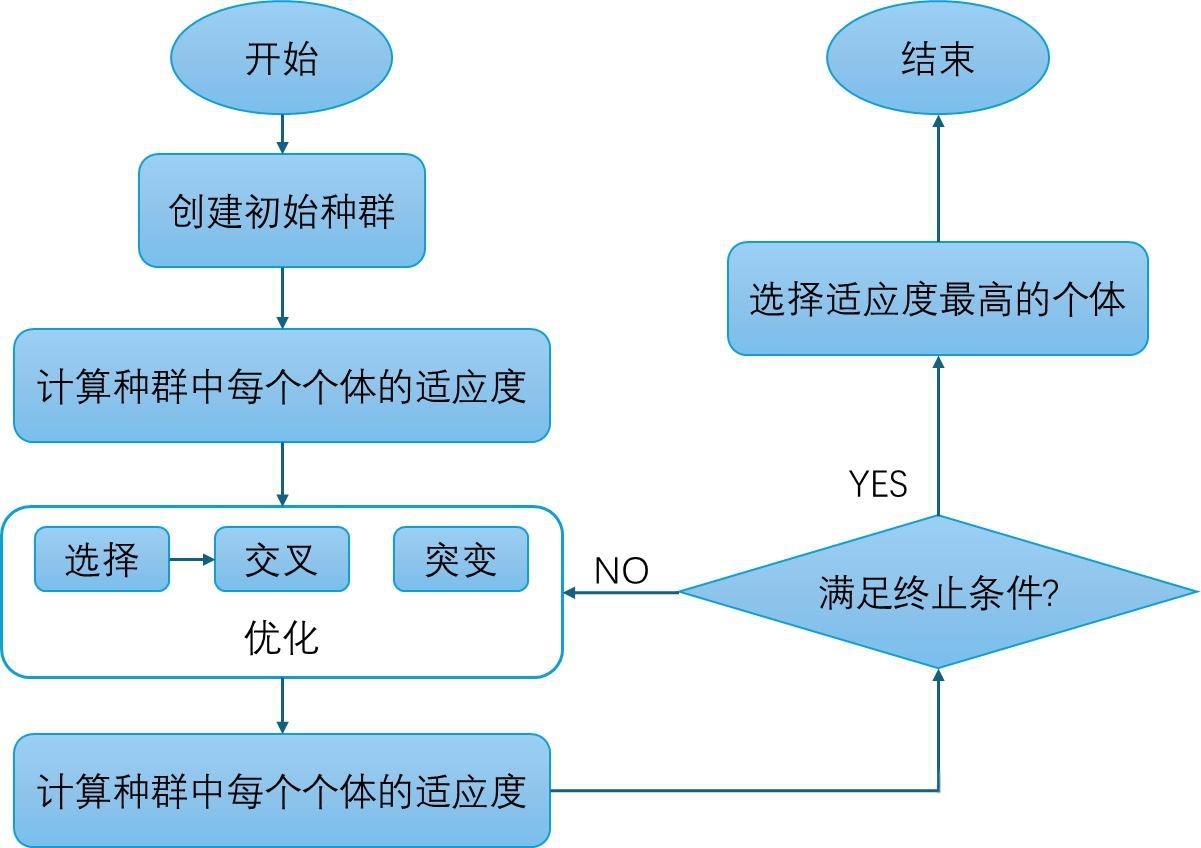
遗传算法（Genetic Algorithm, GA）通过模拟自然选择过程求解优化问题，其核心在于“编码-选择-交叉-变异”四个步骤的迭代。该算法具有全局搜索能力，能在高维、非凸、多峰问题中有效逼近最优解。

5.1 基本流程

遗传算法的执行流程可概括为以下步骤：

  • 初始化种群
    将问题解映射为染色体编码（如二进制、实数或排列编码），随机生成初始种群。

  • 计算适应度
    对种群中的每个个体，通过适应度函数评估解的优劣。适应度值通常与目标函数相关，例如TSP问题中可取路径总长度的倒数。

  • 选择父代
    根据适应度高低选择优秀个体作为父代，常用方法包括：

    • 轮盘赌选择：按适应度比例随机选择，适应度高者被选概率大；
    • 锦标赛选择：随机挑选若干个体进行竞争，优者胜出。

  • 交叉生成子代
    将父代个体通过交叉操作产生子代。常见方式：

    • 单点交叉：在染色体某一点切分并交换后段；
    • 多点交叉：在多个切点进行交换；
    • 顺序交叉（OX）：适用于排列编码，如TSP路径。

  • 变异操作
    对子代基因以较小概率进行变异，以维持群体多样性。变异方式包括交换两个基因位置、反转片段或随机替换。

  • 更新种群
    将子代加入种群，按策略（如精英保留）选择下一代个体，保持种群规模恒定。

  • 判断终止条件
    若达到最大代数或适应度满足阈值，算法终止，输出最优解。

5.2 关键算子解析

选择算子：

  • 轮盘赌：个体被选概率 \(p_{i} = \frac{f_{i}}{\sum f_{j}}\)pi​=∑fj​fi​​，简单直观，但易早熟收敛。
  • 锦标赛选择：随机抽取k个个体，选择适应度最高者，能维持多样性。

交叉算子：

  • 单点交叉：适合二进制编码；
  • 多点交叉：增强探索性；
  • 顺序交叉（OX）：保持排列问题的合法性，常用于TSP。

变异算子：

  • 交换变异：交换路径中两点位置；
  • 反转变异：反转某段路径顺序；
  • 随机替换：随机修改基因值。

5.3 案例：遗传算法求解TSP

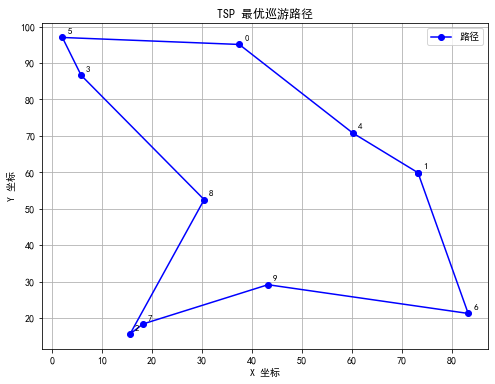
问题描述：

给定若干城市及其坐标，寻找一条最短路径使旅行商访问所有城市并回到起点。

关键设计：

  • 编码方式：用城市编号排列表示路径；
  • 适应度函数：路径长度的倒数；
  • 交叉算子：顺序交叉（OX）保持路径合法性；
  • 变异算子：交换两个城市位置。

Python实现示例

import numpy as np
import random
import matplotlib.pyplot as plt

# 添加中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']   # 中文字体
plt.rcParams['axes.unicode_minus'] = False     # 解决负号显示问题

# 计算路径总长度
def path_length(path, coords):
    length = 0
    for i in range(len(path)):
        length += np.linalg.norm(coords[path[i]] - coords[path[(i + 1) % len(path)]])
    return length

# 适应度函数：路径长度的倒数
def fitness(path, coords):
    return 1 / (1 + path_length(path, coords))

# 顺序交叉（OX）
def order_crossover(p1, p2):
    size = len(p1)
    start, end = sorted(random.sample(range(size), 2))
    child = [-1] * size
    child[start:end] = p1[start:end]
    ptr = end
    for city in p2[end:] + p2[:end]:
        if city not in child:
            if ptr >= size:
                ptr = 0
            child[ptr] = city
            ptr += 1
    return child

# 交换变异
def swap_mutation(path):
    a, b = random.sample(range(len(path)), 2)
    path[a], path[b] = path[b], path[a]
    return path

# 遗传算法主流程
def genetic_algorithm(coords, pop_size=100, generations=500, pc=0.8, pm=0.1):
    num_cities = len(coords)
    population = [random.sample(range(num_cities), num_cities) for _ in range(pop_size)]

    for gen in range(generations):
        fits = [fitness(p, coords) for p in population]
        new_population = []

        # 精英保留
        elite = population[np.argmax(fits)]
        new_population.append(elite)

        # 生成下一代
        while len(new_population) < pop_size:
            parents = random.sample(population, 5)
            parent1 = max(parents, key=lambda p: fitness(p, coords))
            parents = random.sample(population, 5)
            parent2 = max(parents, key=lambda p: fitness(p, coords))

            # 交叉
            if random.random() < pc:
                child = order_crossover(parent1, parent2)
            else:
                child = parent1[:]

            # 变异
            if random.random() < pm:
                child = swap_mutation(child)

            new_population.append(child)

        population = new_population

    # 返回最优解
    best = min(population, key=lambda p: path_length(p, coords))
    return best, path_length(best, coords)

# 绘制巡游路径
def plot_path(coords, path, title="TSP 最优巡游路径"):
    plt.figure(figsize=(8, 6))
    ordered_coords = coords[path + [path[0]]]  # 回到起点
    plt.plot(ordered_coords[:, 0], ordered_coords[:, 1], 'o-', color='blue', label='路径')
    for i, (x, y) in enumerate(coords):
        plt.text(x + 1, y + 1, str(i), fontsize=9)
    plt.title(title)
    plt.xlabel('X 坐标')
    plt.ylabel('Y 坐标')
    plt.grid(True)
    plt.legend()
    plt.show()

# 测试
if __name__ == "__main__":
    np.random.seed(42)
    random.seed(42)
    # 随机生成10个城市坐标
    coords = np.random.rand(10, 2) * 100
    best_path, best_length = genetic_algorithm(coords)
    print("最佳路径:", best_path)
    print("路径长度:", best_length)
    plot_path(coords, best_path)  # 绘制巡游图

六、遗传算法未来发展与应用

6.1 未来发展趋势

遗传算法未来的发展呈现深度融合与智能演化两大方向。首先，在深度学习领域，遗传算法通过神经架构搜索（NAS）与进化强化学习优化网络结构与超参数，尤其适用于无法获取梯度信息的黑箱优化问题，在自动机器学习（AutoML）中前景广阔。其次，在多目标优化与决策支持方面，多目标遗传算法（如MOGA、NSGA-II）可同时平衡成本、性能等冲突目标，结合可视化与决策分析方法，为智能制造、交通调度和能源分配提供更优方案。再次，量子计算的融合带来突破契机，量子遗传算法（QGA）利用量子叠加与干涉并行搜索，有望显著提升大规模组合优化效率。最后，自适应与在线进化成为新热点，算法参数可随环境与种群状态动态调整，实现实时优化与持续演化，为动态环境下的无人驾驶、智能运维等应用奠定基础。

6.2 应用领域拓展

遗传算法以其全局搜索能力，已广泛应用于工程优化、路径规划、调度问题、机器学习超参数优化等领域。在智能制造中，GA用于生产线调度与资源分配；在交通领域，支持最优路径与信号灯控制设计；在金融与能源管理中，帮助实现投资组合优化和电力调度。近年来，GA逐渐扩展到生物信息学（基因序列分析、药物分子设计）与新材料设计（分子结构搜索、性能预测）等新兴领域，展现出跨学科应用潜力。

6.3 面临的挑战与展望

尽管遗传算法具有广泛适用性，但仍存在计算代价高、收敛速度慢、易早熟收敛等问题。在未来研究中，如何通过混合策略（结合局部搜索、差分进化等）、多目标进化框架以及并行化与分布式计算平台优化性能，是核心突破方向。同时，GA在动态环境与实时优化中的适应性仍待提升。展望未来，遗传算法有望在人工智能自主决策、自动化设计、智慧城市等领域发挥更大作用，并成为下一代智能优化技术的重要支撑。

七、遗传算法之父：霍兰德生平与贡献

7.1 生平简介

约翰·霍兰德（John Henry Holland，1929-2015）是美国著名计算机科学家、复杂系统理论的先驱，也是遗传算法（Genetic Algorithm, GA）的创始人。他出生于美国印第安纳州，早年对数学与工程表现出极强兴趣。霍兰德本科毕业于麻省理工学院（MIT），随后在密歇根大学获得博士学位，并在该校计算机科学与心理学系长期任教直至退休。
在20世纪60-70年代，计算机科学尚处于萌芽期，人工智能研究也刚刚起步。霍兰德敏锐地意识到，传统的确定性算法难以解决具有高度复杂性与不确定性的适应性问题。他提出，应该借鉴自然界中生物进化与遗传机制，用“群体搜索”代替单一解搜索，通过迭代优化模拟自然选择的过程。这一思想直接促成了遗传算法的诞生。
霍兰德不仅在学术上取得巨大成就，还培养了大量后继研究者，其学生和合作者在进化计算、复杂系统、适应性代理等领域均有卓越贡献，对人工智能的发展产生深远影响。

7.2 主要贡献

霍兰德的贡献可概括为三个方面：

（1）遗传算法与模式定理

霍兰德在1975年出版的《Adaptation in Natural and Artificial Systems》中首次系统化提出遗传算法，定义了编码、选择、交叉、变异等操作，并通过**模式定理（Schema Theorem）**解释算法为何能在进化过程中保留并扩散优良基因片段。他的研究使遗传算法从经验性启发式方法提升为有数学基础的理论框架，奠定了进化计算的基石。

（2）复杂适应系统理论

霍兰德提出“复杂适应系统（Complex Adaptive Systems, CAS）”概念，用以描述由多个相互作用的适应性代理组成的系统，如生态系统、市场经济、社会网络等。他认为，这些系统通过局部规则与适应性学习形成整体行为，其演化规律可以用类似遗传算法的机制建模。这一理论极大推动了跨学科研究，对经济学、社会学、生态学均有重要影响。

（3）跨学科桥梁作用

霍兰德的研究不仅局限于计算机科学，他将遗传算法应用于心理学（人类认知模型）、经济学（市场适应行为）、生物学（进化动力学）等领域。他的跨界思维使遗传算法成为一种通用的计算范式，推动了人工智能与复杂系统科学的交叉融合。

7.3 荣誉与影响

霍兰德一生获得众多荣誉，包括：

  • 美国国家科学院院士（National Academy of Sciences）；
  • 美国艺术与科学学院院士（American Academy of Arts and Sciences）；
  • 国际复杂系统研究领域最高荣誉之一——MacArthur Fellowship；
  • 多次获得人工智能与计算机科学领域的重要奖项和荣誉博士学位。

他的学术成果影响深远，被誉为“进化计算之父”。至今，遗传算法及其衍生方法仍在机器学习、优化、人工生命等领域广泛应用。

八、总结

遗传算法作为最早的进化计算方法之一，不仅在优化与搜索问题中取得成功，更深刻影响了人工智能的发展路线。其核心思想——通过群体进化探索复杂搜索空间——突破了传统梯度法与确定性算法的局限，为后续蚁群算法、粒子群优化、差分进化等元启发式方法提供了基础框架。
回顾历史，遗传算法经历了从理论提出（1970s）到应用扩展（1990s）、再到混合改进与并行化（2000s）、以及**与深度学习融合（2010s至今）**的演化历程。其生命力在于持续适应新技术环境，并不断拓展应用边界。遗传算法不仅是一种优化工具，更是一种跨越生物学、计算机科学与复杂系统科学的思维方式。它启示我们：复杂系统的适应性与智能性可以通过简单规则涌现，而不依赖全局控制。随着人工智能从“计算”走向“智能”，遗传算法将在未来继续发挥重要作用。

参考文献

  1. Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. University of Michigan Press.
  2. Goldberg, D. E. (1989). Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley.
  3. Mitchell, M. (1996). An Introduction to Genetic Algorithms. MIT Press.
  4. Eiben, A. E., & Smith, J. E. (2003). Introduction to Evolutionary Computing. Springer.
  5. Wikipedia: Genetic algorithm — 提供了算法历史、原理与应用的概述性资料。
posted @ 2025-08-03 13:40  郝hai  阅读(471)  评论(0)    收藏  举报