从任务分配到匈牙利算法：指派问题的提出、发展与应用

指派问题作为组合优化领域的经典模型，广泛应用于生产调度、交通运输、人工智能等多个领域。20世纪中叶，美国数学家哈罗德·库恩基于匈牙利数学家早期的图论成果，提出了系统高效的匈牙利算法。

“匈牙利算法以其巧妙的矩阵变换和匹配策略，完美解决了指派问题这一组合优化难题。哈罗德·库恩的贡献不仅推动了运筹学发展，更奠定了优化算法设计的经典范式。”

目录

一、引言：指派问题与组合优化的经典范式

指派问题（Assignment Problem）是运筹学和组合优化中最具代表性的经典模型之一，其核心目标是：在资源与任务一一匹配的约束下，寻找最小成本或最大效益的分配方案。这一问题在数学上具有简洁的形式，但在现实应用中却无处不在，从传统工业调度到现代人工智能系统任务分配，都直接依赖其求解方法。

指派问题最初源于对任务分配与成本最优的需求。例如，工厂如何将不同熟练度的工人分配到各道工序以最短时间完成生产任务？航空公司如何安排机组成员执行多条航线以降低疲劳和成本？在多机器人系统或人工智能协作场景中，如何高效地分配子任务以节省能源和提高响应速度？这些看似多样化的问题，都可以抽象为一个统一的数学模型：给定一个成本矩阵，将 n 个资源与 n 个任务一一对应，使总成本达到最小。
指派问题与运输问题、最大流问题有密切联系。运输问题处理的是多供给点与多需求点之间的最优流量分配，而指派问题可视为其规模相等、约束更严格的特例；同时，在图论中，指派问题等价于带权二分图的最优完美匹配，这为后续算法研究提供了重要的图论工具。
在 20 世纪中叶，传统的单纯形法在处理大规模指派问题时效率有限，迫切需要新的多项式时间算法。美国数学家 哈罗德·W·库恩（Harold W. Kuhn） 于 1955 年借鉴匈牙利学派 König 与 Egerváry 的图论成果，提出了著名的 匈牙利算法（Hungarian Algorithm）。这一算法不仅实现了多项式时间求解，还首次将线性规划思想与图论方法有机融合，成为组合优化的里程碑。

今天，匈牙利算法已成为计算机科学、运筹学和人工智能领域的基础算法，广泛应用于物流调度、图像匹配、机器人协作与生物信息学等场景，其理论价值与工程实用性历久弥新。

二、指派问题的历史起源与理论基础

2.1 早期任务分配问题

指派问题的思想可以追溯到 19 世纪末运输问题与资源分配需求的研究。当时的数学家主要关注如何在供需匹配中降低运输成本。这一类问题的研究为后来的指派模型提供了雏形。
20 世纪 30–40 年代，匈牙利数学家在图论领域取得了两项关键性成果：

  • König 定理（1931）
    König 证明了二分图最大匹配数等于最小顶点覆盖数，这一结果首次建立了匹配与覆盖之间的等价关系，为后续算法提供了理论基础。
  • Egerváry 定理（1939）
    Egerváry 推广了 König 定理到带权情形，指出赋权二分图的最大权匹配等于最小权顶点覆盖的权值。该结论直接启发了后来的匈牙利算法，使得通过零元素寻找完美匹配成为可能。

这些成果虽然未直接提出算法，但为指派问题的多项式解法奠定了坚实的数学基石。

2.2 运筹学与线性规划的兴起

二战期间，运筹学作为一门跨学科的决策科学迅速崛起。康托洛维奇（Leonid Kantorovich）在 1939 年提出线性规划模型来解决苏联木材工业的资源配置问题，这是最早将数学优化应用于经济计划的实践。随后，乔治·达齐格（George Dantzig）于 1947 年发明了单纯形法，极大地推动了线性规划求解的普及。
在此背景下，指派问题被迅速识别为运输问题的特例：当供给与需求规模相等且每个资源与任务一一对应时，运输模型简化为指派模型。这一特例的数学性质更优美，解法也更高效，因此吸引了众多研究者的关注。到 20 世纪 50 年代，随着图论与线性规划的交汇，指派问题逐渐发展为组合优化中的核心模型，并最终在库恩提出匈牙利算法时达到理论与算法的统一。

三、库恩的生平与学术背景

3.1 早年经历

哈罗德·威廉·库恩（Harold William Kuhn）于 1925 年 7 月 29 日出生在美国加利福尼亚州圣迭戈。他少年时期即展现出极高的数学天赋，热衷于解几何与数论难题。二战期间，库恩加入美国海军航空兵服役，从事导航与气象计算工作。这段经历使他熟悉实际问题中的资源优化需求，也为其日后研究运筹学埋下伏笔。战后，库恩凭借退伍军人政策进入 普林斯顿大学 数学系，并迅速完成学士、硕士及博士学位，博士论文以组合优化为主题。

3.2 学术氛围与研究起点

普林斯顿在 20 世纪中叶是运筹学和博弈论的学术中心，聚集了冯·诺依曼、纳什、塔克等大师。库恩的博士导师阿尔伯特·塔克是线性规划与对偶理论的奠基人，同时深度参与博弈论发展。这样的环境让库恩既接触到线性规划的最新进展，又受到博弈论中匹配与均衡思想的启发，从而对组合优化与任务分配问题产生了浓厚兴趣。

3.3 核心贡献

1955 年，库恩提出匈牙利算法，首次为指派问题提供了多项式时间解法。这一算法基于匈牙利学派 König 与 Egerváry 的图论成果，被誉为组合优化领域的里程碑。除匈牙利算法外，库恩还与导师塔克合作提出了著名的 KKT 条件（Kuhn-Tucker 条件），成为非线性规划的核心理论。同时，他推动纳什均衡在扩展型博弈中的应用，促进了博弈论与经济学的融合。

3.4 学术荣誉与影响

库恩曾任国际数学联盟要职，并积极参与优化教育的推广。他在 2000 年获颁 约翰·冯·诺依曼理论奖，以表彰其在优化算法与组合数学方面的奠基性贡献。其研究成果至今仍是运筹学与计算机科学的核心教材内容。

3.5 晚年与思想遗产

库恩晚年持续关注人工智能与运筹学的结合，提出优化算法将在智能决策系统中扮演核心角色的前瞻观点。他于 2014 年 7 月 2 日去世，享年 89 岁，留下了横跨算法、博弈论与优化理论的思想遗产。

四、指派问题的数学模型与性质

4.1 问题定义

指派问题（Assignment Problem）是运筹学中最具代表性的组合优化问题之一，其目标是在资源与任务一一对应的条件下，实现全局最优分配。形式化地说，给定 \(n\) 个工人和 \(n\) 个任务，每个工人完成每个任务的成本（或效益） \(c_{i j}\)​ 已知，要求为每个工人分配一个唯一的任务，使总成本最小（或效益最大）。该问题不仅是运输问题的特例，更是后续二分图匹配、网络流优化的重要基础。

4.2 数学建模

指派问题可抽象为0-1 整数规划模型，其决策变量定义为：

\[x_{ij} = \begin{cases} 1, & \text{若工人 } i \text{ 被分配到任务 } j \\ 0, & \text{否则} \end{cases} \]

目标函数为最小化总成本：

\[\text{Minimize}\quad Z = \sum_{i = 1}^{n} \sum_{j = 1}^{n} c_{i j} x_{i j} \]

约束条件包括：

  1. 每个工人必须恰好分配一个任务：

\[\sum_{j = 1}^{n} x_{i j} = 1 , i = 1 , 2 , \ldots , n \]

  1. 每个任务必须恰好分配给一名工人：

\[\sum_{i = 1}^{n} x_{i j} = 1 , j = 1 , 2 , \ldots , n \]

  1. 二进制约束：

\[x_{ij} \in \{0, 1\} \]

该模型虽然是整数规划，但由于其约束矩阵具有全单纯性（Totally Unimodular），线性松弛后的最优解天然为整数，因此可以直接用线性规划或匈牙利算法高效求解。

4.3 图论解释

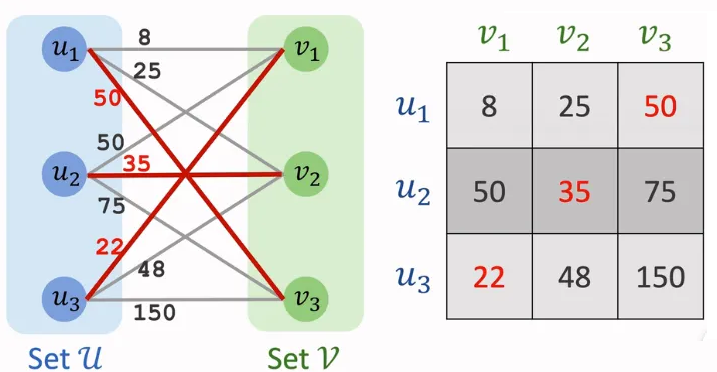
在图论中，指派问题可视为带权二分图的最小权完美匹配问题。

  • 左侧顶点表示工人，右侧顶点表示任务；
  • 边权为工人执行任务的成本 \(c_{i j}\)；
  • 寻找一组不相交边，使所有顶点匹配且总边权最小。

这种图模型不仅清晰揭示了问题本质，也为后续使用网络流、最小费用最大流等算法扩展提供了基础。

五、匈牙利算法的提出与核心思想

5.1 历史背景

指派问题在 20 世纪初已被数学家从图论角度研究，其中 König 定理（1931） 和 **Egerváry 定理（1939）**揭示了最大匹配与最小覆盖之间的关系，为后续算法提供了理论支撑。然而，这些定理仅停留在存在性与等价性层面，缺乏高效的计算步骤。
1955 年，美国数学家 哈罗德·W·库恩（Harold W. Kuhn） 综合匈牙利数学家 König 与 Egerváry 的成果，提出了匈牙利算法（Hungarian Algorithm）。该算法首次将定理转化为系统的多项式时间算法，解决了指派问题长期以来的计算瓶颈，并在《Naval Research Logistics Quarterly》发表论文《The Hungarian Method for the Assignment Problem》，从此成为组合优化领域的里程碑成果。

5.2 核心思想

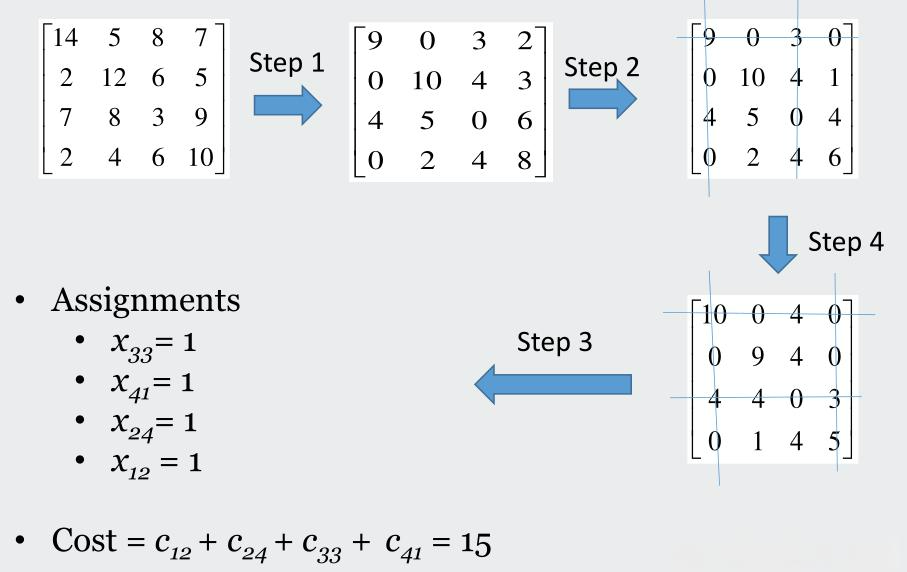
匈牙利算法的关键在于行列减法生成零元素、利用零元素匹配并不断调整矩阵，直到获得完美匹配。其主要步骤如下：

  • 行减法：每行元素减去该行最小值，使每行至少有一个零。
  • 列减法：在行减法结果基础上，每列减去该列最小值，使每列至少有一个零。
  • 零元素匹配：在矩阵零元素位置寻找最大匹配，可视作二分图匹配问题。
  • 最少线覆盖：用最少的行或列覆盖所有零元素，若覆盖线数等于 \(n\)，则匹配完成。
  • 矩阵调整：若覆盖线数小于 \(n\)，取未覆盖元素的最小值 \(k\)：
    • 未覆盖元素减去 \(k\)；
    • 双覆盖元素加上 \(k\)；
    • 生成更多零元素后重复匹配步骤。

这种方法利用矩阵结构特性，将组合优化问题转化为迭代线性运算，算法复杂度为 \(O \left(\right. n^{3} \left.\right)\)，在当时被视为极高效的解法。

5.3 算法流程图

flowchart TD A[输入成本矩阵] --> B[行减法: 每行减去行最小值] B --> C[列减法: 每列减去列最小值] C --> D[寻找零元素最大匹配] D --> E{匹配数 = n?} E -- 是 --> F[输出最优分配方案] E -- 否 --> G[用最少线覆盖所有零] G --> H[调整矩阵: 生成新的零元素] H --> D

匈牙利算法步骤说明：

  • 输入成本矩阵
    用户提供一个表示各工人执行各任务成本的矩阵，作为算法的输入基础。

  • 行减法与列减法
    对矩阵的每一行，减去该行中的最小值；然后对每一列，减去该列中的最小值。这样保证矩阵中至少存在零元素，为后续匹配做准备。

  • 寻找零元素最大匹配
    在经过行列减法调整的矩阵中，寻找覆盖零元素的最大匹配，即尽可能多地为任务分配工人，使得分配中成本为零的元素被利用。

  • 判断匹配数并调整矩阵

    • 如果匹配数等于任务数，说明找到了最优分配，算法结束。
    • 若匹配数小于任务数，则用最少的行或列覆盖所有零元素，调整未覆盖元素的数值，生成新的零元素，继续回到第3步进行匹配。

六、算法改进、扩展与现代应用

6.1 Munkres 改进

库恩在 1955 年提出匈牙利算法后不久，James Munkres 于 1957 年对该方法进行了系统改进，被称为 Kuhn–Munkres 算法。改进的重点在于零元素匹配策略的优化：通过更高效的路径搜索与标号调整方法，减少了冗余匹配步骤，使算法更适合在计算机上实现。尽管其时间复杂度仍为 \(O \left(\right. n^{3} \left.\right)\)，但在实际运算中显著提升了运行效率和稳定性，因此成为目前教科书与工业实现中的标准版本。

6.2 与网络流的关系

指派问题可视作**最小费用最大流（Minimum Cost Maximum Flow）**的特例：

  • 左右两侧节点分别表示工人和任务，边权为指派成本；
  • 在容量均为 1 的二分图中，寻找最小费用的最大流即为求解最优指派方案。

这种等价关系为算法拓展提供了契机：

  • 当问题规模较大或存在非方阵任务分配时，可通过构造虚拟节点与边扩展至网络流模型；
  • 在多约束指派问题（如任务优先级、时间窗口限制）中，也可借助最小费用流算法引入额外约束，解决复杂调度场景。

6.3 现代应用领域

匈牙利算法及其改进版本广泛应用于现代工业与信息科学领域：

  • 制造业与工业工程
    用于工厂排班、设备维护计划、自动化流水线资源分配，可降低生产成本并提升产能利用率。
  • 交通运输与物流调度
    在航班机组分配、出租车与乘客实时匹配、港口作业任务调度等领域应用广泛，可优化运输效率和服务质量。
  • 计算机视觉
    在多目标跟踪（Multi-Object Tracking）中，通过匈牙利算法进行帧间目标关联，解决“数据关联问题”，是视频监控、无人驾驶的重要技术环节。
  • 人工智能多智能体系统
    在多机器人协作、无人机编队中，用于分配任务、优化协同路径，尤其在实时性要求高的环境中表现优异。

这些应用场景充分展示了算法从理论模型到工程实践的跨越。

6.4 局限与改进方向

尽管匈牙利算法在方阵指派问题中表现优异，但也存在局限：

  • 仅适用于方阵问题，若资源与任务数量不相等，需要通过虚拟节点扩展模型，效率略有下降；
  • 难以处理动态任务分配（任务实时到达或资源实时变化）及多目标优化（同时考虑成本与时间）；
  • 在超大规模数据（如上万节点）中，算法的 \(O \left(\right. n^{3} \left.\right)\) 时间复杂度仍显沉重。

未来研究方向主要包括：

  • 并行化与分布式实现，利用多核或 GPU 提升算法速度；
  • 近似算法与启发式方法，在保证可接受精度的前提下加速求解；
  • 与深度学习结合，利用神经网络预测匹配初始解或引导搜索，提升在动态环境下的适应性。

七、案例分析：出租车调度问题

假设某城市有4辆出租车和4位乘客，需将出租车分配给乘客以最小化总行驶距离。我们将各辆出租车到乘客的距离作为成本，利用匈牙利算法找到最优指派方案。

7.1 成本矩阵

乘客1 乘客2 乘客3 乘客4
出租车1 12 7 9 7
出租车2 8 9 6 6
出租车3 7 17 12 14
出租车4 15 14 6 6

矩阵表示为：

\[C = \begin{bmatrix} 12 & 7 & 9 & 7 \\ 8 & 9 & 6 & 6 \\ 7 & 17 & 12 & 14 \\ 15 & 14 & 6 & 6 \end{bmatrix} \]

7.2 求解步骤概述

  • 构造成本矩阵，表示出租车到乘客的距离。
  • 应用匈牙利算法，通过行减法、列减法、零元素匹配和调整矩阵，找到最小总距离的完美匹配。
  • 输出最优指派结果，即每辆出租车对应的乘客。

7.3 Python代码示例

import numpy as np
from scipy.optimize import linear_sum_assignment
import matplotlib.pyplot as plt
from matplotlib import rcParams

# 设置支持中文字体（以微软雅黑为例）
rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 指定默认字体
rcParams['axes.unicode_minus'] = False  # 解决负号 '-' 显示为方块的问题

# 成本矩阵（距离）
cost_matrix = np.array([
    [12, 7, 9, 7],
    [8, 9, 6, 6],
    [7, 17, 12, 14],
    [15, 14, 6, 6]
])

# 使用匈牙利算法（线性和分配）
row_ind, col_ind = linear_sum_assignment(cost_matrix)

# 输出匹配结果
print("最优分配方案：")
total_cost = 0
for r, c in zip(row_ind, col_ind):
    print(f"出租车 {r+1} → 乘客 {c+1}, 距离: {cost_matrix[r, c]}")
    total_cost += cost_matrix[r, c]
print(f"总最小距离: {total_cost}")

# 可视化匹配图
plt.figure(figsize=(8,6))
plt.title("出租车与乘客匹配示意图")

# 出租车和乘客坐标（虚拟二维位置用于展示）
taxi_pos = np.array([[1,4], [2,4], [3,4], [4,4]])
passenger_pos = np.array([[1,1], [2,1], [3,1], [4,1]])

plt.scatter(taxi_pos[:,0], taxi_pos[:,1], c='blue', label='出租车', s=100)
plt.scatter(passenger_pos[:,0], passenger_pos[:,1], c='red', label='乘客', s=100)

for r, c in zip(row_ind, col_ind):
    plt.plot([taxi_pos[r,0], passenger_pos[c,0]], [taxi_pos[r,1], passenger_pos[c,1]], 'k--')

for i, (x,y) in enumerate(taxi_pos):
    plt.text(x, y+0.2, f"出租车{i+1}", ha='center', color='blue')
for i, (x,y) in enumerate(passenger_pos):
    plt.text(x, y-0.3, f"乘客{i+1}", ha='center', color='red')

plt.legend()
plt.axis('off')
plt.show()

八、总结与未来展望

匈牙利算法作为组合优化领域的经典算法，奠定了任务分配问题求解的理论和实践基础。自库恩于1955年提出该算法以来，它凭借多项式时间复杂度和对指派问题特殊结构的深度利用，成为运筹学、计算机科学及人工智能领域不可或缺的工具。
在智能制造、智慧物流、交通调度和多智能体系统等现代应用中，匈牙利算法持续发挥着重要作用，帮助实现资源的科学调配和效率的最大化。同时，随着数据规模和应用复杂性的不断提升，传统算法面临着大规模实时调度与动态环境的挑战。
未来的研究方向应聚焦于算法的并行化实现、动态任务分配的在线算法设计，以及与机器学习技术的融合，推动算法智能化和自适应化发展。哈罗德·库恩跨学科的研究精神和创新方法为当前和未来的优化算法设计提供了宝贵范例，激励学术界和产业界不断突破与创新，推动优化理论和应用迈向新的高度。

参考文献

  1. Kuhn, H. W. (1955). The Hungarian Method for the Assignment Problem. Naval Research Logistics Quarterly, 2(1–2), 83–97.
  2. Munkres, J. (1957). Algorithms for the Assignment and Transportation Problems. Journal of the Society for Industrial and Applied Mathematics, 5(1), 32–38.
  3. Burkard, R. E., Dell’Amico, M., & Martello, S. (2009). Assignment Problems. SIAM.
  4. Papadimitriou, C. H., & Steiglitz, K. (1998). Combinatorial Optimization: Algorithms and Complexity. Dover Publications.
  5. Kuhn-Tucker 条件及其应用，见《线性规划与最优化》相关教材。
posted @ 2025-07-26 06:25  郝hai  阅读(739)  评论(0)    收藏  举报