旅行商问题的先声：哈密尔顿巡游游戏的数学之美

在数学史上，有许多问题因其简洁的表述和深刻的内涵，成为推动数学发展和应用的催化剂。哈密尔顿（William Rowan Hamilton）便是这样一位先驱，他不仅以力学和代数的杰出贡献闻名，更因其对“巡游游戏”（Hamiltonian cycle）概念的提出，成为旅行商问题（TSP）及图论领域的奠基人。19世纪的数学环境中，哈密尔顿将代数与几何的思想巧妙融合，开辟了新的研究方向。巡游游戏看似简单的路径问题，实则暗含组合优化与离散数学的核心难题，至今仍是计算机科学、运筹学、物理等多学科研究的热点。

“哈密尔顿的巡游游戏，表面看似简单的路径问题，实则蕴藏深刻的数学结构与智慧。它不仅启迪了图论的发展，也成为优化与计算领域的核心难题，激励无数学者不断探索。

一、引言：从天才少年到科学巨匠

19世纪的欧洲，是科学与数学不断革新、思想激荡的黄金时代。工业革命的浪潮席卷而来，带动了工程技术和应用科学的飞速发展。与此同时，天文学、光学以及力学领域也在迅猛进步，促使人类对自然界的认知不断深化和拓展。正是在这样一个充满机遇与挑战的时代背景下，威廉·罗恩·哈密尔顿（William Rowan Hamilton，1805–1865）应运而生，成为了那段历史中最耀眼的数学和物理巨匠之一。

哈密尔顿自幼展现出过人的才华。年幼时，他不仅精通多国语言，还是一位数学神童。据传，他8岁时就能够熟练运算微积分问题，15岁时发表了第一篇数学论文。这样卓越的数学天赋为他后续在力学和代数领域的开创性工作奠定了坚实基础。哈密尔顿的研究不仅仅停留在理论层面，他勇于打破传统思维，尝试用创新的数学工具来解释复杂的物理现象，成为连接古典与现代物理学的重要桥梁。
哈密尔顿最为人称道的贡献之一是他提出的哈密尔顿力学。这一理论以变分法为基础，系统地描述了物理系统的动力学行为，极大地丰富和完善了牛顿力学体系。哈密尔顿力学后来发展成为量子力学和经典力学的核心框架，对现代物理学产生了深远影响。通过对能量函数（即哈密尔顿函数）的研究，哈密尔顿成功将动力学问题转化为数学分析问题，为后来诸如辛几何和守恒定律的研究铺平了道路。
与此同时，哈密尔顿还创造了另一项划时代的数学成果——四元数代数。这是一种扩展复数的数学体系，由四个分量组成，开创了高维代数的先河。四元数的引入不仅极大地推动了代数结构的研究，也为计算机图形学、物理学中的旋转描述以及机器人运动学等现代技术领域提供了强有力的数学工具。四元数因其独特的性质和实用价值，至今仍在科学与工程界被广泛应用。
除了严肃的理论研究，哈密尔顿还富有创意和趣味性。他设计并推广了著名的巡游游戏（Icosian Game），这是一种基于正二十面体顶点的路径寻找游戏，要求玩家找到一条经过每个顶点且只经过一次的闭合路径。虽然看似简单，这款游戏实际上涉及到图论中的“哈密尔顿回路”问题，也就是后人熟知的旅行商问题的早期雏形。巡游游戏不仅成为当时数学娱乐的一部分，也激发了对图论和组合优化问题的深入研究，成为现代计算机科学和运筹学领域的重要基础。
哈密尔顿的学术成就跨越了多个学科领域，理论与应用并重，严肃与趣味结合。他的思想和成果不仅推动了19世纪数学与物理的发展，更为20世纪的科学革命奠定了坚实基础。人们评价他是“连接经典与现代物理的桥梁”，这不仅仅是对他学术贡献的认可，更是对其跨领域创新精神的高度赞誉。

在下文里，我们将详细梳理哈密尔顿的生平经历，深入探讨他的主要学术贡献，并解析他提出的代表理论与数学公式。同时，也将展示巡游游戏的趣味设计和它对现代科学技术的深远影响。让我们走进这位伟大数学家和物理学家的世界，感受旅行商问题背后那份永恒的数学之美。

二、早年生平与学术成长

2.1 童年与早期天赋

威廉·罗恩·哈密尔顿于1805年8月4日出生在爱尔兰都柏林郊区的克隆塔夫（Dublin, Clontarf）。他的家庭文化氛围浓厚，父亲是一名律师，母亲出身书香门第，家庭重视教育，为哈密尔顿的成长提供了良好的环境。哈密尔顿从小就表现出卓越的学习能力，尤其在语言方面展现出惊人的天赋。他4岁时便能熟练使用拉丁语和希腊语，这在当时的教育环境中极为罕见。到10岁之前，他已经掌握了包括拉丁语、希腊语、法语、意大利语、德语等共计十三种语言，因此被誉为“语言神童”。
然而，随着年龄的增长，哈密尔顿的兴趣逐渐从语言转向数学。12岁那年，他开始系统地学习欧几里得几何、代数和数学分析，并展现出对抽象数学概念的非凡理解力。与同龄人相比，他不仅能够轻松掌握已有的数学知识，还能提出独到的见解和思考方法。哈密尔顿自学能力极强，经常在父亲的图书馆中钻研各种数学著作，尤其对几何学和数论产生了浓厚的兴趣。
这段童年时期的经历奠定了哈密尔顿扎实的数学基础和广博的知识视野，为他后来的科学探索奠定了坚实的根基。哈密尔顿不仅拥有超群的智力，更有极强的好奇心和求知欲，这些品质成为他日后成为科学巨匠的重要推动力。

2.2 大学时期与数学成就初露

1823年，18岁的哈密尔顿考入都柏林三一学院（Trinity College Dublin），主修数学和物理。在大学期间，哈密尔顿的学术潜力迅速显现，他不仅在课堂上表现优异，还积极投身于科学研究。他利用课余时间广泛涉猎数学、物理和天文学领域的前沿知识，并开始发表学术论文。
在都柏林三一学院的几年间，哈密尔顿发表了多篇重要论文，内容涵盖几何学、光学以及力学领域，表现出跨学科的卓越才能。1827年，仅21岁的他被任命为爱尔兰皇家天文台的台长，成为当时最年轻的皇家天文学家。这一职位不仅体现了他在科学界的卓越声誉，也为他提供了施展才华的平台。
在天文台工作期间，哈密尔顿致力于研究光学中的特征函数方法，为描述光的传播提供了数学工具。这一工作为后来物理学中的波动理论奠定了基础。与此同时，他还开始探索动力学的数学描述，逐步构建起后来的哈密尔顿力学框架。通过引入能量函数和变分原理，他实现了对牛顿力学的系统化和推广，开创了力学的新纪元。
大学及早期职业阶段，哈密尔顿表现出独特的数学直觉和跨学科视野。他不仅注重理论的深度，更关注如何将数学应用于物理实际问题。这一时期的学术积累为他后续在四元数代数和图论方面的开创性贡献奠定了坚实基础，也预示着他将成为19世纪最具影响力的数学家和物理学家之一。

三、学术贡献与理论体系

3.1 哈密尔顿力学

3.1.1 理论框架

哈密尔顿力学是经典力学的重要分支，与牛顿力学和拉格朗日力学并列，是理解物理系统动力学的核心理论之一。它的最大特点在于用相空间的思想，将系统的状态通过一组广义坐标 $q_i$ 和共轭动量 $p_i$ 来完整描述。核心工具是哈密尔顿函数 $H(q,p,t)$，通常对应于系统的总能量（动能与势能之和）。这一函数的引入，使得复杂的动力学问题能够被转化为求解一组正则方程：

\[\dot{q_i} = \frac{\partial H}{\partial p_i}, \qquad \dot{p_i} = -\frac{\partial H}{\partial q_i} \]

这里，$\dot{q_i}$ 和 $\dot{p_i}$ 分别表示广义坐标和动量对时间的导数。通过这组方程，哈密尔顿力学将运动方程转化为对偏导数的分析问题，极大地简化了对多自由度系统的研究。同时，这种方法强调能量守恒和对称性，揭示了物理系统深层的几何结构。

3.1.2 对现代物理的影响

哈密尔顿力学不仅在经典物理中有着不可替代的地位，更成为现代物理学的重要基石：

量子力学：量子力学的薛定谔方程中，哈密尔顿算符 $\hat{H}$ 是系统能量的量子对应物。哈密尔顿力学的数学形式为量子动力学的建立提供了理论框架。
天体力学：计算行星轨道及卫星运动时，哈密尔顿方法通过相空间和正则变换简化了复杂天体系统的动力学分析。
控制理论与优化：Pontryagin极大值原理中引入的哈密尔顿函数，启发了控制系统的优化方法，广泛应用于工程和经济学领域。

这种理论的推广不仅深化了我们对物理规律的理解，也推动了数学中的辛几何、守恒律和对称性理论的发展。

3.2 四元数代数

3.2.1 概念提出

1843年，哈密尔顿在思考如何扩展复数到更高维代数时，首次提出了四元数的概念。四元数形式为：

\[q = a + bi + cj + dk \]

其中 $a, b, c, d$ 为实数，$i, j, k$ 是虚数单位，满足非交换的乘法规则：

\[i^2 = j^2 = k^2 = ijk = -1 \]

这是数学史上首次出现的非交换代数结构，突破了传统代数对乘法交换律的限制，开启了高维代数体系的新纪元。哈密尔顿甚至在都柏林的哈伯桥上刻下这条公式，象征其发现的重大意义。

3.2.2 应用价值

四元数因其独特的代数性质和几何解释，至今在多个领域发挥重要作用：

三维旋转：四元数能有效表示空间旋转，避免了欧拉角中的万向锁问题，提供了更稳定的旋转计算方法。
计算机图形学：在3D动画和模型中，四元数用于插值旋转和姿态控制，简化了计算过程并提高精度。
航空航天：飞行器姿态控制系统利用四元数实现精确稳定的导航和定位，极大提升了飞行安全性和操控性能。

四元数的引入，不仅丰富了代数学结构，也成为现代工程技术中的核心数学工具。

3.3 光学与波动理论

哈密尔顿在光学领域也作出卓越贡献，特别是提出了特征函数方法，用以研究光线传播和波动传播的路径选择问题。他发展出的哈密尔顿光线方程，结合几何光学和波动理论，精确描述了光线在介质中的传播轨迹和折射规律。
这一方法对后来的工程光学设计，如光纤传输、激光技术等领域产生了直接影响。哈密尔顿光线理论强化了光学的数学基础，为现代光学工程提供了理论支持。

3.4 组合数学与巡游游戏

3.4.1 巡游游戏设计

1857年，哈密尔顿设计了一款趣味性极强的数学游戏——二十面体巡游游戏（Icosian Game）。游戏基于正二十面体的结构，玩家需要找到一条路径，从某个顶点出发，经过所有顶点一次且仅一次，最终回到起点。这种路径即现在称为的哈密尔顿圈。
该游戏不仅是数学娱乐，更是深刻的组合优化问题的体现。哈密尔顿巧妙地将几何与代数相结合，通过游戏形式引发公众和学术界对路径问题的关注。

3.4.2 对图论的启发

哈密尔顿巡游游戏被视为哈密尔顿圈问题的最早实例，开启了组合图论的研究新方向。此后，该问题演变成著名的旅行商问题（TSP），成为运筹学和计算机科学中最经典、最具挑战性的优化问题之一。
旅行商问题涉及在给定城市集合中寻找最短巡回路径，广泛应用于物流配送、芯片设计、机器人路径规划等多个现代领域。哈密尔顿的这一游戏不仅启发了数学家对图结构的研究，也推动了算法设计和复杂性理论的发展。

哈密尔顿的学术贡献横跨理论物理、代数学、光学和组合数学领域，他的理论体系不仅奠定了19世纪科学的基础，更成为现代科技进步的重要源泉。通过对哈密尔顿力学、四元数代数及巡游游戏的探讨，我们得以窥见这位科学巨匠跨学科思维的非凡智慧和对数学美的执着追求。

四、巡游游戏与Python实现

4.1 旅行商问题（Traveling Salesman Problem, TSP）

旅行商问题是组合优化领域的经典问题，目标是在给定的一组城市中寻找一条最短的巡回路径，使得每个城市恰好被访问一次，且最终回到起点。该问题广泛应用于物流配送、路径规划、芯片设计等实际场景。

TSP 数学模型

Minimize

\[\sum_{(i,j) \in A} c_{ij} x_{ij} \]

subject to

\[\sum_{j \in V \setminus \{i\}} x_{ij} = 1, \quad \forall i \in V \]
\[\sum_{i \in V \setminus \{j\}} x_{ij} = 1, \quad \forall j \in V \]
\[\sum_{i \in S} \sum_{j \in S} x_{ij} \leq |S| - 1, \quad \forall S \subseteq V, \ |S| \geq 2 \]
\[x_{ij} \in \{0,1\}, \quad \forall (i,j) \in A \]

决策变量定义

\[x_{ij} = \begin{cases} 1, & \text{若路径中包含从节点 } i \text{ 到节点 } j \text{ 的边} \\ 0, & \text{否则} \end{cases} \quad \forall (i,j) \in A \]

其中：

$ V $ 是所有节点（城市）的集合；
$ A = {(i,j) \mid i,j \in V, i \neq j} $ 是所有可能的有向弧（边）的集合；
$ c_{ij} $ 表示从城市 $ i $ 到城市 $ j $ 的旅行成本（距离、时间等）。

目标函数

最小化总旅行成本：

\[\min \sum_{(i,j) \in A} c_{ij} \, x_{ij} \]

约束条件

每个城市恰好被访问一次（出度约束）

\[\sum_{j \in V, j \neq i} x_{ij} = 1, \quad \forall i \in V \]

含义：从每个城市 $i$ 出发，必须恰好有一条边指向其他城市，即每个城市的出度为1。

每个城市恰好被访问一次（入度约束）

\[\sum_{i \in V, i \neq j} x_{ij} = 1, \quad \forall j \in V \]

含义：每个城市 $j$ 必须恰好被一条来自其他城市的边指向，即每个城市的入度为1。

子回路消除约束（Subtour Elimination）

\[\sum_{i \in S} \sum_{j \in S} x_{ij} \leq |S| - 1, \quad \forall S \subset V, \; |S| \geq 2 \]

含义：对于任何非空真子集 $S$，子集内部的边数不能形成完整回路，防止出现多个独立的子回路，确保路径是一个单一的哈密顿回路。

变量取值约束

\[x_{ij} \in \{0,1\}, \quad \forall (i,j) \in A \]

含义：决策变量为二进制变量，表示路径边是否被选中。

约束总结表

约束编号	数学表达式	实际含义
(1)	$\sum_{j \in V \setminus \{i\}} x_{ij} = 1$	每个城市必须恰好离开一次（出度为1）。
(2)	$\sum_{i \in V \setminus \{j\}} x_{ij} = 1$	每个城市必须恰好到达一次（入度为1）。
(3)	$\sum_{i \in S} \sum_{j \in S} x_{ij} \leq \|S\| - 1$	消除子回路，确保解是单一的哈密顿回路。
(4)	$x_{ij} \in \{0,1\}$	决策变量为二元变量。

补充说明

约束(1)和(2)保证每个城市恰好被访问一次，形成一个排列，但单独使用时可能产生多个子回路。
约束(3)由Dantzig-Fulkerson-Johnson首次提出，是模型的核心难点。其数量随城市数指数增长，实际求解复杂。
为提高效率，约束(3)通常被替换为Miller-Tucker-Zemlin (MTZ)等多项式规模的子回路消除约束，便于求解。

该整数线性规划模型准确刻画了旅行商问题的基本结构，是理论研究和算法设计的重要基础。

4.2 二十面体图构建与哈密尔顿圈搜索

下面代码展示如何生成二十面体图，并自动搜索哈密尔顿圈路径：

import networkx as nx
import matplotlib.pyplot as plt
from matplotlib import rcParams

# 中文显示支持
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False

# ----------- 1. 生成二十面体图 -----------
G = nx.icosahedral_graph()

# ----------- 2. 寻找哈密尔顿圈 -----------
def find_hamiltonian_cycle(graph):
    n = graph.number_of_nodes()
    path = [0]  # 从顶点0出发

    def backtrack(v):
        if len(path) == n:
            if path[0] in graph[path[-1]]:
                return path + [path[0]]
            return None
        for u in graph.neighbors(v):
            if u not in path:
                path.append(u)
                result = backtrack(u)
                if result:
                    return result
                path.pop()
        return None

    return backtrack(0)

hamilton_cycle = find_hamiltonian_cycle(G)

# ----------- 3. 计算节点位置并作图 -----------
pos = nx.spring_layout(G, dim=3, seed=42)
pos_2d = {k: (v[0], v[1]) for k, v in pos.items()}

plt.figure(figsize=(8, 6))

# 基础边（蓝色，粗5倍）
nx.draw_networkx_edges(G, pos_2d, alpha=0.4, width=2)

# 节点
nx.draw_networkx_nodes(G, pos_2d, node_color='lightblue', node_size=400)
nx.draw_networkx_labels(G, pos_2d, font_size=18)

# 高亮哈密尔顿圈（红色，线更粗）
if hamilton_cycle:
    edge_path = list(zip(hamilton_cycle[:-1], hamilton_cycle[1:]))
    nx.draw_networkx_edges(G, pos_2d, edgelist=edge_path, edge_color='red', width=3)

plt.title("哈密尔顿巡游游戏：二十面体图（高亮哈密尔顿圈）", fontsize=20)
plt.axis('off')
plt.show()

# 输出找到的哈密尔顿圈
print("找到的哈密尔顿圈路径:", hamilton_cycle)

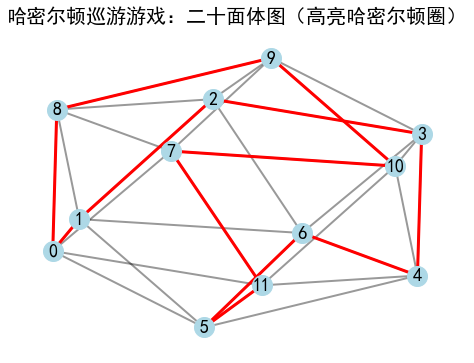
4.3 结果与分析

在图示中，蓝色线条代表了二十面体图的所有边，粗细加大以增强视觉效果，方便观察整个多面体的结构。二十面体作为正多面体之一，具有20个面和12个顶点，连接边的排列非常规则，适合用来展示复杂的路径问题。红色加粗路径即为程序搜索到的哈密尔顿圈，这条路径覆盖了所有顶点且回到起点，满足哈密尔顿回路的定义。
该哈密尔顿圈的高亮显示清晰地展现了遍历所有顶点的闭合路径，直观反映了巡游游戏的核心思想。通过该示例，可以让读者更好地理解旅行商问题的几何本质，以及哈密尔顿圈在组合图论中的重要地位。同时，结合Python代码的实现过程，不仅使理论更加具体，也为学习者提供了编程实践的范例，有助于掌握图论算法的设计和应用。
此外，二十面体图作为三维结构的二维投影，展示了哈密尔顿圈在复杂空间图中的搜索难度与解决方法，强调了图论与计算机算法的紧密结合。此图示与代码结合的教学方式，有助于激发读者对图论与优化问题的兴趣和进一步探索的动力。

五、学术影响与现代应用

5.1 力学与量子物理

哈密尔顿在经典力学中提出的哈密尔顿函数（Hamiltonian）为描述物理系统能量和动力学演化提供了全新的数学框架。进入20世纪，随着量子力学的发展，哈密尔顿函数被直接继承并推广为哈密尔顿算符（Hamiltonian operator），成为量子态演化的核心。薛定谔方程中，哈密尔顿算符描述系统的总能量及其对量子态的作用，揭示微观世界的基本规律。哈密尔顿力学的理论框架不仅深化了物理学对守恒律和对称性的理解，还促进了现代物理学中辛几何和对称群理论的发展，成为连接经典力学与现代物理的重要桥梁。

5.2 图论与计算机科学

哈密尔顿设计的巡游游戏揭示了遍历图中所有顶点且仅访问一次的路径问题，开创了哈密尔顿圈的研究方向。该问题进一步发展成为旅行商问题（TSP），成为组合优化领域的标志性难题。TSP不仅理论意义深远，涉及NP完全性和算法复杂性理论的核心问题，也推动了启发式算法、整数规划和分支限界法的发展。旅行商问题广泛应用于物流路径规划、芯片设计、车辆调度和网络路由等领域，对现代计算机科学中的算法设计与复杂性分析产生了深刻影响。哈密尔顿圈与TSP问题促进了图论、运筹学和人工智能等学科的交叉融合。

5.3 工程与计算机图形

1843年哈密尔顿提出的四元数代数，为三维空间中的旋转提供了优雅且高效的数学工具。四元数的非交换性质使其在描述空间旋转时避免了传统欧拉角中的万向锁问题，极大提升了稳定性和计算效率。现代计算机图形学、虚拟现实和增强现实技术广泛采用四元数来实现3D模型的旋转与动画插值。在航空航天领域，四元数被用于飞行器姿态控制和卫星导航系统，实现精准且实时的方向调整。此外，机器人运动规划和计算机视觉也因四元数的高效旋转表示而受益。四元数的应用极大推动了现代工程技术的发展，成为计算机图形和空间导航不可或缺的基础工具。

哈密尔顿的理论贡献跨越数学与物理多个领域，其思想不仅在理论科学中奠定基础，也深刻影响了现代技术与工程实践。无论是量子物理的深层描述，还是图论与计算机科学的算法突破，以及工程领域的空间旋转控制，哈密尔顿的学术遗产依然焕发着强大的生命力和时代价值。

六、趣闻轶事与人文一面

威廉·罗恩·哈密尔顿不仅是卓越的数学家和物理学家，更是一位具有丰富人文情怀和多才多艺的学者。他的学术生涯中流传着许多有趣而感人的故事，展现了这位科学巨匠独特的人格魅力和人文精神。

最著名的轶事莫过于哈密尔顿在都柏林布罗姆桥（Broom Bridge）上刻下四元数乘法公式的事件。1843年10月16日，当他终于突破复数在三维空间无法扩展的难题，发现四元数的非交换乘法规则后，他激动地在这座桥的石栏上用刀刻下了公式：

\[i^{2} = j^{2} = k^{2} = i j k = - 1 \]

这段铭文成为数学史上的经典传奇，也象征着他对数学世界的巨大贡献。如今，布罗姆桥成为数学爱好者的朝圣之地，每年都有许多人前来纪念这一历史性时刻。
除了在数学上的卓越成就，哈密尔顿还是一位诗人和哲学爱好者。他热衷于文学，经常在学术讲座和交流中引用莎士比亚、但丁等文学巨匠的名句，将科学与艺术巧妙结合，展现出他对生命、宇宙和人类存在的深刻思考。这种跨界的学术风格，使他的讲座生动且富有感染力，激励了无数学生和同行。
哈密尔顿以谦逊、平和的性格著称。他对学生关怀备至，善于启发他们的独立思考，强调理论与实践的结合。他严谨却不失温情的人格魅力，使得他的学术团队气氛融洽，培养出一批批杰出的科学人才。

这些趣闻轶事和人文侧面，丰富了我们对哈密尔顿这位科学家的认识，彰显了他不仅是冷冰冰的公式背后的数学家，更是拥有深厚情怀与人格魅力的时代巨匠。

七、总结：跨越时代的数学交响

威廉·罗恩·哈密尔顿的一生，是天才与创新的传奇篇章。他在经典力学中提出的哈密尔顿力学，不仅完善了牛顿体系，也为量子力学奠定了数学基础，成为物理学中的桥梁。他创造的四元数代数，开辟了非交换代数的新领域，成为现代计算机图形学、航空航天姿态控制等技术的核心工具。更为独特的是，他设计的巡游游戏激发了哈密尔顿圈和旅行商问题的研究，推动了图论与组合优化的发展。
跨越数学、物理与计算机科学，哈密尔顿的思想如同一场跨时代的交响乐，深刻影响了众多学科的演进。无论是在算法竞赛中攻克旅行商问题，还是在工程应用中利用四元数实现精确旋转，我们都能感受到这位19世纪伟大数学家的远见卓识和非凡创造力。他的学术遗产，激励着一代又一代科学家不断探索未知，续写数学与科学的辉煌篇章。

哈密尔顿以卓越才智架起数学与物理桥梁，其理论与思想跨越时空，激励后人不断探索科学未知。

八、参考文献与延伸阅读

Hamilton, W. R. Lectures on Quaternions (1853)
哈密尔顿本人讲授四元数的经典著作，系统介绍了四元数的代数结构与几何意义，是理解四元数及其应用的权威资料。
Goldstein, H. Classical Mechanics (3rd Edition)
这是经典力学领域的标准教材，详细讲解了哈密尔顿力学的理论基础与实际应用，适合物理和工程专业的读者。
Gross, Jonathan L., and Yellen, Jay. Graph Theory and Its Applications (2nd Edition, 2005)
本书全面介绍图论的基本概念与经典问题，涵盖哈密尔顿圈及旅行商问题等重要内容，是图论学习和研究的重要参考。
Cormen, Thomas H., et al. Introduction to Algorithms (3rd Edition)
作为计算机科学领域的权威教材，本书对组合优化、NP完全性和相关算法进行了深入阐述，帮助读者理解旅行商问题的计算复杂性。
Wikipedia: William Rowan Hamilton
维基百科页面提供了哈密尔顿生平、学术贡献及趣闻轶事的综合介绍，适合快速浏览和了解人物背景。
Wolfram MathWorld: Hamiltonian Cycle
MathWorld提供了哈密尔顿圈的数学定义、性质及相关算法介绍，是数学爱好者和研究者的实用在线资源。

这些文献涵盖哈密尔顿的核心理论、相关数学工具以及现代应用，为深入学习哈密尔顿贡献和旅行商问题提供了丰富的资料支撑。无论是数学、物理，还是计算机科学领域的读者，都能从中获得系统而全面的知识。

posted @ 2025-07-28 08:05 郝hai 阅读(249) 评论(0) 收藏举报

刷新页面返回顶部

约束编号	数学表达式	实际含义
(1)	\(\sum_{j \in V \setminus \{i\}} x_{ij} = 1\)	每个城市必须恰好离开一次（出度为1）。
(2)	\(\sum_{i \in V \setminus \{j\}} x_{ij} = 1\)	每个城市必须恰好到达一次（入度为1）。
(3)	\(\sum_{i \in S} \sum_{j \in S} x_{ij} \leq \|S\| - 1\)	消除子回路，确保解是单一的哈密顿回路。
(4)	\(x_{ij} \in \{0,1\}\)	决策变量为二元变量。

haohai9309

格物致知，知行合一！