步入约束优化的核心：拉格朗日乘数法的数学美学

在现代科学与工程的诸多领域中，优化问题无处不在。如何在多种限制条件下找到最优解，既是理论数学的经典难题，也是实际应用中的关键挑战。约束优化作为其中的重要分支，依赖于一套强大而优雅的数学工具，而拉格朗日乘数法正是这套工具中的核心法宝。
诞生于18世纪的拉格朗日乘数法，不仅开启了带约束极值问题的代数化处理，也将解析力学和数学优化紧密连接起来。它将复杂的约束条件转化为乘数引入的辅助变量，形成统一的优化框架，使得问题的解法从几何直观到代数表达无缝对接。如今，随着计算能力和算法的发展，拉格朗日乘数法不仅在物理、经济、工程领域持续发光发热，更在人工智能和机器学习中的约束优化任务中发挥着举足轻重的作用。

“我将用最一般的方法——纯粹代数的方法，来处理力学问题。”
—— 约瑟夫·路易·拉格朗日
这句话凝练了拉格朗日毕生追求的数学理想，也为后世开辟了现代约束优化和解析力学的新纪元。拉格朗日乘数法正是在这一理念指引下诞生，成为跨越数学与应用的桥梁。

📑 目录

一、引言

“用最普适、最优雅的数学思想，去理解和改造现实世界。”
这不仅是拉格朗日毕生的追求，也是他留给后世最珍贵的精神财富。作为18世纪最杰出的数学家之一，约瑟夫·路易·拉格朗日通过其独创的乘数法，将看似复杂的约束优化问题化繁为简，奠定了现代优化理论的坚实基础。
拉格朗日乘数法不仅是数学分析中的一个巧妙工具，更是跨越物理学、经济学、工程学乃至人工智能等多领域的核心方法。它通过引入辅助变量，将约束条件直接融入目标函数，实现了从复杂多条件系统中寻找最优解的有效路径。正因如此，掌握这一方法不仅意味着掌握一门数学技巧，更意味着打开理解复杂系统与决策优化的大门。
本文将从拉格朗日的生平故事切入，带你深入理解乘数法的数学美学与几何直觉，结合实际案例展示其广泛应用，并展望未来技术发展对该方法的推动。无论你是数学爱好者、工程师，还是数据科学从业者，都能在这里找到理解约束优化核心利器的钥匙。

二、拉格朗日的传奇人生

2.1 早年求学与学术启蒙

约瑟夫·路易·拉格朗日（Joseph-Louis Lagrange）于1736年1月25日出生在意大利都灵，这座城市当时属于萨丁-皮埃蒙特王国。他出生于一个法裔-意裔混血家庭，父亲是一位公职人员，但家境并不富裕，后来因为一次投资失败，家里的经济状况进一步恶化。尽管如此，拉格朗日在少年时期展现出了极高的学习天赋。
早年的拉格朗日原本遵从家族意愿，开始学习法律，希望能够从事公务员职业。然而，他的兴趣很快被数学所吸引，尤其是在17岁时自学了数学基础知识后，对天文学和数学产生了浓厚兴趣。传说他曾阅读英国著名天文学家哈雷（Edmund Halley）的论文，被其中严密的数学推理和宇宙规律的美妙联系深深震撼。此后，他毅然决然地放弃了法律学业，转而投身数学研究，自学成才，展现出极强的自律与独立探索精神。
当时，都灵的数学教育资源相对有限，但拉格朗日通过自学和大量阅读欧拉、牛顿等大师的著作，迅速成长为一名才华横溢的年轻数学家。他的早期作品多聚焦于微积分和代数学，尤其对解析函数和无穷级数表现出非凡兴趣。18岁时，他成为都灵炮兵学校的数学助教，这一职位不仅赋予他教学的机会，也为他提供了学术交流的平台。

2.2 柏林与巴黎的科学岁月

1764年，拉格朗日凭借对月球运动及月亮章动问题的深刻研究，赢得了法国科学院颁发的大奖。这一荣誉不仅让他在国际数学界声名鹊起，也成为其事业的重要转折点。1766年，他受普鲁士国王腓特烈大帝的邀请，前往柏林担任柏林科学院数学主任。此后，他在柏林度过了将近二十年的时间，成为欧洲数学的领军人物。
在柏林时期，拉格朗日发表了大量重要论文，涵盖微分方程、变分法、力学等多个领域。他不仅延续和发展了欧拉和牛顿的研究成果，还将数学推向更高的抽象层次。柏林科学院也成为当时欧洲数学研究的重要中心，拉格朗日在这里培养了众多优秀学生和学者，奠定了其在数学史上的领导地位。
1787年，拉格朗日应法国科学院邀请迁居巴黎，进入科学生涯的新阶段。巴黎大革命期间，尽管社会动荡，他依然保持科研工作的连续性和高产量。他积极参与法国度量衡制度的改革工作，推动科学与国家建设的紧密结合。拿破仑崛起后，拉格朗日成为法国科学院终身会员、巴黎理工学院首席教授，并获封帝国勋爵，享受极高的社会荣誉。

2.3 科学全才与传承

拉格朗日不仅在数学理论方面卓有建树，更是一位名副其实的科学全才。他的研究领域广泛，涵盖解析学、微分方程、变分法、数论、概率论以及物理学中的力学和天文学。他最具代表性的贡献之一，是在1788年发表的巨著《解析力学》（Mécanique analytique）。这部著作将经典力学的所有问题用纯代数和分析方法加以统一表达，彻底改变了物理学的数学基础，并为后来的理论物理和数学物理奠定了坚实的基石。
此外，拉格朗日在微分方程解法、三体问题研究、行星运动理论等方面均做出卓越贡献。他提出的“拉格朗日乘数法”成为解决带约束优化问题的基本方法，至今仍是数学、物理、经济和工程领域中不可或缺的工具。
拉格朗日的学术影响力通过他的学生得以延续。傅里叶、泊松等人均受其直接指导，继承并发扬光大了他的科学思想。拉格朗日点——太阳和行星引力平衡的位置——和数学中的拉格朗日函数等概念，更是永远铭刻着他的名字。

在他漫长而光辉的科学旅程中，拉格朗日以其严谨的逻辑、广博的学识和对数学美的追求，成为连接古典数学与现代数学桥梁的重要人物。他的贡献不仅深刻影响了当时的科学发展，也为现代科学技术的蓬勃发展提供了基础。

三、拉格朗日乘数法的数学美学

3.1 方法起源与基本思想

拉格朗日乘数法诞生于18世纪，是约瑟夫·路易·拉格朗日在研究变分法和解析力学过程中提出的一种优雅而有效的数学工具。其核心目的是解决带有约束条件的极值问题。传统的极值问题通常只涉及对一个目标函数求极大或极小值，而实际问题往往伴随着诸如资源限制、结构约束等多种条件。这些约束条件使得问题变得更加复杂，直接求解极值变得困难。

拉格朗日的巧妙之处在于将约束条件以“乘数”的形式融入目标函数中，形成一个新的函数——拉格朗日函数，将原本的带约束极值问题转化为无约束问题，从而可以运用无约束优化的经典方法来寻找极值。这种方法不仅理论优美，而且计算便捷，极大地拓宽了数学优化的应用范围。

3.2 乘数法的几何直观

拉格朗日乘数法的本质可以通过几何视角来理解。考虑在空间中有一个约束曲面定义为

\[g(x) = c \]

我们希望在该曲面上找到函数

\[f(x) \]

的极值点。极值点的一个关键性质是：在该点处，目标函数 $ f $ 的梯度方向 $ \nabla f $ 必须与约束曲面 $ g $ 的梯度方向 $ \nabla g $ 平行。换句话说，梯度向量之间存在比例关系：

\[\nabla f(x) = -\lambda \nabla g(x) \]

其中，比例系数 $ \lambda $ 即为“拉格朗日乘数”。这个关系体现了目标函数的变化率在约束条件作用下被“调节”，使得在约束曲面上的方向导数为零，实现极值。

该几何直观说明，极值点不仅满足目标函数梯度消失的条件，同时还必须尊重约束曲面的形状，二者的梯度向量方向紧密耦合。乘数 $ \lambda $ 可以理解为约束对极值点的“推力”或“权衡”，平衡了目标函数的优化与约束条件的限制。

3.3 数学表达式与推导

基于上述思想，我们定义拉格朗日函数：

\[\mathcal{L}(x, \lambda) = f(x) + \lambda (g(x) - c) \]

该函数将原问题的目标函数 $ f(x) $ 和约束条件 $ g(x) = c $ 融合到一个统一的表达式中。求解带约束的极值问题转化为寻找使拉格朗日函数在所有变量 $ x_i $ 和乘数 $ \lambda $ 上的梯度均为零的点，即满足：

\[\frac{\partial \mathcal{L}}{\partial x_i} = 0, \quad i = 1, 2, \ldots, n \]

\[\frac{\partial \mathcal{L}}{\partial \lambda} = g(x) - c = 0 \]

展开第一条式子，等价于

\[\nabla f(x) + \lambda \nabla g(x) = 0 \]

这正是前述梯度平行的数学表达。同时，约束条件 $ g(x) = c $ 也必须被满足。由此形成的方程组共同确定了极值点的位置与乘数值。

这种处理方法不仅将复杂的约束极值问题转为求解方程组的问题，还带来了乘数 $ \lambda $ 的额外意义——它反映了约束条件变化对最优值的敏感度，因而在经济学等领域拥有重要解释力。

3.4 多约束与不等式扩展

在实际应用中，问题往往不止一个约束，而是多个等式甚至不等式约束。针对多个等式约束 $ g_i(x) = c_i $，乘数法推广为：

\[\mathcal{L}(x, \lambda) = f(x) + \sum_{i} \lambda_i (g_i(x) - c_i) \]

这里，每个约束 $ g_i $ 对应一个拉格朗日乘数 $ \lambda_i $，联合构成一个更高维的乘子向量。极值条件同样是对 $ x $ 和所有 $ \lambda_i $ 求偏导，构成多元非线性方程组。

对于不等式约束 $ h_j(x) \leq d_j $，经典乘数法难以直接适用，但现代优化理论通过引入卡罗什-库恩-塔克（Karush-Kuhn-Tucker, KKT）条件将乘数法推广，实现了对不等式约束的有效处理。KKT条件不仅包含拉格朗日乘数，还包含互补松弛条件，使得优化解的可行域得到合理界定。

乘数法因其理论完备和计算便捷，成为现代非线性规划和约束优化问题的基石，在工程设计、经济资源分配、机器学习参数优化等多领域得到广泛应用。其数学美学体现在将目标函数和约束无缝融合，通过一套统一的极值条件精确捕捉系统平衡的本质。

至此，拉格朗日乘数法从起源、几何直观到多约束推广，展现出数学的简洁之美与强大适用性。后续章节将带你进入实际应用与算法演化的精彩世界。

四、拉格朗日乘数法的实战应用

4.1 物理力学中的经典应用

拉格朗日在《解析力学》中，将经典力学问题转化为解析表达，约束条件如轨迹、能量守恒，都通过乘数法引入，极大简化运动方程求解。

4.2 经济学与工程中的优化问题

在经济学中，拉格朗日乘数法被用来求解效用最大化和成本最小化问题，如预算约束下的消费选择。工程领域，如结构设计、流体动力学中也普遍采用该方法实现约束条件下的优化。

4.3 机器学习与智能系统中的约束优化

现代机器学习中，诸如带约束的参数训练、安全强化学习、资源分配均用乘数法或其变种保证算法在约束范围内高效运行。

4.4 Python示例实战演示



import sympy as sp
import numpy as np
import matplotlib.pyplot as plt

# -------------------------------------------------
# 1. 原始符号计算（与题目相同）
# -------------------------------------------------
x, y, lam = sp.symbols('x y lam')
f = x * y
g = x**2 + y**2 - 1
L = f + lam * g

eqs = [sp.diff(L, var) for var in (x, y, lam)]
solutions = sp.solve(eqs, (x, y, lam))

print("满足约束的极值点：")
for sol in solutions:
    print(sol)

# -------------------------------------------------
# 2. 把符号解转成数值，方便画图
# -------------------------------------------------
extrema = [(float(s[0]), float(s[1])) for s in solutions]

# -------------------------------------------------
# 3. 作图
# -------------------------------------------------
fig, ax = plt.subplots(figsize=(6, 6))

# 画约束圆 x² + y² = 1
theta = np.linspace(0, 2*np.pi, 400)
ax.plot(np.cos(theta), np.sin(theta), 'k-', lw=2, label=r'$x^2+y^2=1$')

# 画极值点
for (x_, y_) in extrema:
    ax.plot(x_, y_, 'ro')
    ax.annotate(f'({x_:.2f}, {y_:.2f})',
                xy=(x_, y_), xytext=(5, 5),
                textcoords='offset points',
                color='red', fontsize=9)

# 画目标函数 f = xy 的等高线
x_grid, y_grid = np.meshgrid(np.linspace(-1.2, 1.2, 400),
                             np.linspace(-1.2, 1.2, 400))
z_grid = x_grid * y_grid
levels = np.linspace(-0.5, 0.5, 11)
cs = ax.contour(x_grid, y_grid, z_grid, levels, colors='gray', linestyles='dashed', linewidths=0.6)
ax.clabel(cs, inline=True, fontsize=8, fmt='%1.2f')

# 美化
ax.set_aspect('equal')
ax.set_xlabel('x')
ax.set_ylabel('y')
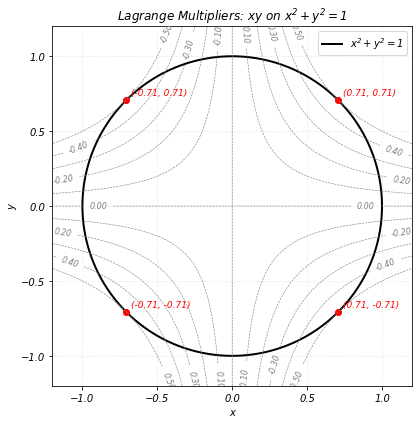
ax.set_title('Lagrange Multipliers: $xy$ on $x^2+y^2=1$')
ax.legend()
ax.grid(True, ls=':', alpha=0.4)

plt.tight_layout()
plt.show()

五、拉格朗日乘数法的未来演化与趋势

5.1 算法改进与数值优化

随着计算能力的不断提升和优化理论的发展，传统的拉格朗日乘数法在算法层面也经历了重要改进。其中，增强拉格朗日法（Augmented Lagrangian Method）和交替方向乘子法（Alternating Direction Method of Multipliers, ADMM）成为处理大规模非凸优化问题的两大主力军。增强拉格朗日法通过引入惩罚项，使得原本难以收敛的约束问题得以更稳定地求解，极大地提升了算法的鲁棒性和收敛速度。ADMM则将复杂的优化问题拆解成若干子问题交替求解，适合分布式计算环境，特别适用于机器学习和信号处理中的大规模约束优化。

这些数值算法的进步使得拉格朗日乘数法不仅限于理论分析，更能应对现实中海量数据和复杂约束的挑战，成为现代工程与科学计算中的核心工具。

5.2 深度学习与安全强化学习中的应用

深度学习模型通常具有海量参数，且训练过程中常伴随多种约束，如参数范数限制、资源消耗约束等。将拉格朗日乘数法嵌入深度神经网络训练流程中，能够实现对硬约束的有效控制，从而提升模型泛化能力和训练稳定性。此外，安全强化学习作为人工智能安全领域的前沿方向，依赖于乘数法保证训练策略在满足安全约束的同时最大化奖励。这种方法不仅提升了智能体的鲁棒性，还降低了在现实环境中的风险，推动了自动驾驶、机器人控制等安全关键应用的发展。

5.3 跨学科融合：能源、生物医学与环境

拉格朗日乘数法在多领域的跨学科融合日益凸显。以可再生能源为例，风能和太阳能调度中需解决带有多重约束的非线性优化问题，拉格朗日方法提供了有效的数学框架来协调能源供需平衡。生物医学领域中，医疗资源分配、药物剂量优化等复杂决策问题同样依赖约束优化技术。环境科学方面，污染控制、生态系统保护等问题涉及多目标、多约束的平衡，拉格朗日乘数法帮助科学家实现可持续发展的优化方案。这种跨领域的广泛应用彰显了乘数法作为约束优化核心工具的通用价值。

5.4 教育普及与思维工具化

随着智能时代的到来，解决复杂系统性问题的能力变得尤为重要。拉格朗日乘数法作为数学与工程决策的基石，将更加深入地融入基础教育和跨学科培训体系。通过直观的几何理解、数学推导和计算实践，学生和工程师能够培养严谨的系统思维和问题解决能力。未来，各类教育平台和智能教学工具将更多采用交互式方式，帮助学习者掌握这一核心工具，促进其在人工智能、大数据、自动化等前沿领域的广泛应用。拉格朗日乘数法不仅是数学工具，更是一种思维模式，助力人类驾驭日益复杂的技术挑战。

拉格朗日乘数法正经历着理论与应用的双重升级。未来，伴随算法创新、跨学科融合和教育普及，这一经典方法将在更广阔的领域展现更大价值，持续推动科学技术的进步与社会发展。

六、总结与思考

拉格朗日乘数法作为数学优化领域的经典之作，以其简洁而深刻的数学思想，奠定了现代约束优化的理论基础。它不仅仅是数学家优雅的理论表达，更是工程师、科学家解决实际复杂问题的利器。通过将约束条件与目标函数巧妙结合，拉格朗日乘数法帮助我们在多目标、多条件的现实世界中寻找最优平衡点，体现了数学的力量和智慧。
随着计算技术和算法的不断进步，拉格朗日乘数法也在不断演进。增强拉格朗日法、交替方向乘子法等现代算法的引入，使其在大规模、非凸优化问题中表现更加出色。与此同时，深度学习、安全强化学习、能源管理等新兴领域的广泛应用，进一步证明了其在跨学科问题解决中的不可替代性。拉格朗日乘数法不仅将在理论研究中保持活力，更将在教育普及和实际工程中发挥更大作用。希望更多的学习者和实践者能够深入理解并灵活应用这一经典工具，推动科学技术与社会进步。

“拉格朗日乘数法不仅是优化的利器，更是一种洞察复杂系统平衡的智慧，连接了数学美学与现实挑战的桥梁。”

七、参考文献

  1. MacTutor History of Mathematics: Joseph-Louis Lagrange
    本页面由苏格兰圣安德鲁斯大学数学史档案馆编写，详尽梳理了拉格朗日的生平、科研成果与时代背景。作为数学史权威资料，推荐用于了解其科学轨迹与人物评价。
    链接：MacTutor - Lagrange
  2. 《解析力学》（Mécanique Analytique） - Joseph-Louis Lagrange, 1788
    拉格朗日的代表作，被誉为“力学的代数学革命”。此书首次系统化地以变分法和拉格朗日乘数形式表述经典力学，奠定了现代理论物理与优化理论的数学基础。推荐研读权威中译本或英译本。
  3. Wikipedia: Lagrange Multiplier
    该页面简明介绍了拉格朗日乘数法的数学定义、推导过程及典型应用案例，对初学者和工程从业者提供良好入门路径。内容经过多次同行修订，逻辑清晰，便于快速掌握核心概念。
    链接：Lagrange Multiplier - Wikipedia
  4. J. Nocedal & S. Wright, Numerical Optimization (2nd ed.), Springer, 2006
    该教材是优化领域的权威著作，系统阐述了约束优化方法中的拉格朗日函数、KKT条件、增广拉格朗日法等，适用于研究生与研究人员进阶学习。尤其适合工程优化和机器学习背景。
  5. Stephen Boyd & Lieven Vandenberghe, Convex Optimization, Cambridge University Press, 2004
    一本经典凸优化教材，详细介绍了拉格朗日对偶性、乘子法在现代算法（如ADMM）中的演化，理论与算法结合紧密，是现代机器学习与运筹学不可或缺的参考书籍。书中提供大量代码与案例，便于实践。

🔵 图中各个拉格朗日点

拉格朗日点 位置说明 稳定性 应用实例
L1 太阳与地球之间 不稳定 SOHO太阳观测卫星位置（近太阳）
L2 地球外侧（远离太阳） 不稳定 詹姆斯·韦布空间望远镜（JWST）在此
L3 太阳另一侧，与地球对称 不稳定 理论存在，人造物体极少放置于此
L4 地球轨道前方60° 稳定 潜在地球特洛伊小行星轨道
L5 地球轨道后方60° 稳定 潜在小行星/太空站候选点

posted @ 2025-07-31 05:59  郝hai  阅读(584)  评论(0)    收藏  举报