动态规划:贝尔曼理论的孵化与应用的创新
“动态规划并非一种编程技巧,而是一种思考复杂多阶段决策问题的数学方法。它利用最优子结构的性质,将大问题分解为一系列相互关联的子问题,通过递归式的贝尔曼方程实现整体最优。”
—— 理查德·贝尔曼
在当今复杂多变的决策环境中,如何在多阶段、多变量的条件下实现最优选择,成为科学研究和工程实践中的核心难题。20世纪中叶,理查德·贝尔曼(Richard Bellman)以卓越的数学洞察力,提出了划时代的动态规划理论。这一方法不仅彻底改变了运筹学和最优化领域,也为控制理论、人工智能及现代数据科学奠定了坚实基础。贝尔曼以“分阶段决策”和“递归求解”的思想,巧妙地解决了传统算法难以应对的多阶段决策问题,使复杂系统的优化变得可行且高效。本文将带领读者走进贝尔曼的学术世界,深入理解动态规划的理论根基与广泛应用,领略这位数学大师如何用一套优雅的数学框架推动了智能决策的革命。
目录
一、 引言:数学优化领域的革命者
二、 理查德·贝尔曼的成长背景与学术经历
三、 动态规划理论的诞生背景
四、 动态规划的核心思想与数学模型
五、 经典动态规划问题及算法实例
六、 贝尔曼的学术贡献与社会影响
七、 未来展望:动态规划在智能时代的价值与挑战
八、 总结:贝尔曼与动态规划的时代价值
九、 参考文献
一、引言:数学优化领域的革命者
理查德·贝尔曼(Richard Ernest Bellman)是20世纪最重要的应用数学家之一,被誉为动态规划(Dynamic Programming)之父。他以卓越的直觉和数学洞察,开创了多阶段决策优化的新纪元。1950年代,在面对复杂的军事和工程问题时,贝尔曼提出了一种全新的建模与求解方法——动态规划,它用“分阶段求解”和“最优子结构原理”的思想,极大拓展了人类处理大规模系统问题的能力。
动态规划不仅解决了当时飞行控制、火箭弹道优化等实际问题,更在理论上奠定了现代最优化方法的一个基石。它的核心理念“贝尔曼方程”至今仍在深度学习、强化学习、计算金融、生物信息学、网络路由等领域发挥着巨大作用,成为许多智能算法的根基。
贝尔曼的伟大之处,不仅在于提出了一种方法,更在于他揭示了一种思想模式——如何从局部最优导向整体最优。他的工作改变了工程控制论的发展轨迹,也影响了后续几十年整个运筹学界对问题建模方式的理解。本文将系统回顾贝尔曼的生平、学术背景、动态规划的提出背景与数理结构,剖析其核心理论模型与推导过程,展示其在军事、工业、AI等多个场景下的典型应用,并探讨该理论对后世的深远影响。让我们一起走近这位将“数学思想转化为国家力量”的学术巨匠,理解他如何用一条方程式,推动了一场优化革命。
二、理查德·贝尔曼的成长背景与学术经历
理查德·欧内斯特·贝尔曼(Richard Ernest Bellman)生于1920年8月26日,出生地为美国纽约。他成长在一个知识氛围浓厚的家庭中,从小展现出对数学与逻辑推理的浓厚兴趣。贝尔曼在求学期间展现出非凡的才智,尤其擅长将抽象的数学问题与现实问题相结合。1941年,他以优异成绩从普林斯顿大学本科毕业,并在哈佛大学继续深造,获得数学博士学位。
在第二次世界大战期间,贝尔曼加入了美国国防科研体系,进入加州理工学院以及后来的**兰德公司(RAND Corporation)**工作。在这些顶尖研究机构中,他广泛参与了军事技术和系统工程项目,特别是在火控系统、弹道预测、武器调度和最优路径设计等领域积累了丰富的工程实践经验。这一阶段的经历为他日后提出动态规划理论提供了宝贵的背景与现实动力。
战争带来的巨大计算与调度压力让贝尔曼逐渐认识到,传统的线性规划、穷举搜索等方法在处理多阶段、多变量的复杂系统问题时效率低下,难以应对爆炸式增长的状态空间。他意识到,真正有效的求解框架应具有“阶段性”、“递归性”和“局部最优导向全局最优”等核心特征。正是在这一思想驱动下,贝尔曼在1950年代初提出了“动态规划(Dynamic Programming)”的基本框架。
这一理论一经提出,便迅速获得了学界的广泛关注,并在工程控制、最优路径、资源配置等问题中取得了显著成效。1957年,贝尔曼发表了划时代的专著《Dynamic Programming》,系统阐述了动态规划的基本原理、数学形式及应用框架,标志着该理论的正式确立。这本书不仅奠定了贝尔曼在最优化领域的奠基人地位,也成为运筹学、控制论和人工智能领域的重要参考文献。
贝尔曼的学术道路极具开创性与前瞻性。他通过跨学科的研究实践,将抽象数学变为解决现实问题的利器。他的研究风格强调问题导向、思维递归、结构分析,深刻地影响了后来的系统科学、强化学习乃至智能算法的建模方式。
三、动态规划理论的诞生背景
20世纪中叶,世界正处于科技、工业与军事快速发展的时期。随着生产组织的规模扩大、交通网络的拓展以及军事系统的复杂化,人们越来越频繁地面临一种具有多阶段、动态变化与全局目标的问题:如何在有限资源约束下,进行连续的、互相关联的决策,以达到系统整体的最优效果。
传统的优化方法如穷举法虽然理论上可以穷尽所有组合,但在现实问题中一旦状态空间扩大,计算量将呈指数级增长,完全无法实施。而贪心算法虽然快速,却常常局部最优而非全局最优,缺乏系统性。面对这种困境,亟需一种能处理阶段性依赖、状态演变和全局规划的新型数学方法。
理查德·贝尔曼正是在这样的背景下提出了“动态规划(Dynamic Programming)”这一革命性思想。他注意到,许多复杂问题存在“最优子结构”性质:一个问题的最优解往往可以通过其子问题的最优解递归构建。基于此,贝尔曼引入状态变量描述系统的当前信息,定义控制变量(或决策变量)表示可能的操作,并构建状态转移方程与贝尔曼方程,从而实现逐阶段递推求解最优策略。
这一思想的提出,不仅突破了传统优化在多阶段情境下的瓶颈,也成为后续如控制论、强化学习、最优路径算法等众多领域的理论基础,开启了动态优化方法的新时代。
四、动态规划的核心思想与数学模型
动态规划(Dynamic Programming,简称DP)是处理多阶段最优化问题的一种基本方法,其核心思想在于“将问题分阶段解决、通过状态表示系统信息、通过递归构造最优解”。这一思想由理查德·贝尔曼提出,核心内容可归结为以下几个关键要素:
🔹 阶段划分
首先,将复杂的问题划分为若干个连续的阶段,每个阶段进行一次决策。每个阶段的决策不仅影响当前收益,还决定系统进入哪个状态,从而影响后续所有阶段。
🔹 状态变量定义
用状态变量 \(s_t\) 描述系统在第 \(t\) 阶段的全部信息。状态变量既包含历史信息的摘要,又用于指导本阶段的决策选择。
🔹 决策变量设定
在每个阶段 \(t\),可以选择一个动作(即决策) \(a_t\),从而影响系统状态的演化和当前阶段的收益。
🔹 状态转移函数
状态在各阶段之间是如何演变的,通常通过一个状态转移函数刻画:
这表明系统在采取决策 \(a_t\) 后,从状态 \(s_t\) 转移到下一阶段的状态 \(s_{t+1}\)。
🔹 收益函数
每个阶段获得的即时收益用 \(R_t(s_t, a_t)\) 表示,依赖于当前状态和采取的决策。
🔹 优化目标函数
整个问题的目标是最大化(或最小化)从初始阶段到终止阶段的累积收益总和:
🔹 贝尔曼方程:递归构造最优解
动态规划的核心工具是价值函数(或代价函数),用于刻画从某一状态出发所能获得的最优累计收益。贝尔曼提出用如下递归形式定义价值函数:
其中:
- \(V_t(s_t)\):表示从第 \(t\) 阶段的状态 \(s_t\) 出发,最优策略下可以获得的最大收益;
- \(s_{t+1} = f_t(s_t, a_t)\):状态转移;
- 终止条件:\(V_T(s_T) = \text{终止收益或0}\)。
这一递推公式即为贝尔曼方程(Bellman Equation),它将原问题转化为一系列递归子问题,便于通过“自底向上”或“自顶向下”的方式求解整体最优。几何意义上,贝尔曼方程描述了状态空间中逐阶段的“最优值传播”过程。每个状态的最优值,取决于该状态所能采取的动作以及所带来的后续最优值。最终,从初始状态出发,沿着每个阶段最优决策路径即可得到全局最优策略。
这种递归结构不仅提高了解题效率,还成为强化学习、最短路径、库存控制等领域中最为核心的建模方法。
五、经典动态规划问题及算法实例
动态规划理论催生了大量具有代表性的问题模型和高效算法。其核心思想在于将复杂问题分解为重叠子问题,逐步递推最优解。以下是几个最具代表性的动态规划问题及其模型框架:
5.1 背包问题(Knapsack Problem)
问题描述:
给定 \(n\) 个物品,每个物品有重量 \(w_i\) 和价值 \(v_i\),以及一个容量为 \(W\) 的背包,求如何选择物品使得不超过背包容量的前提下,总价值最大。
动态规划模型构建:
-
状态定义:
\(V(i, w)\) 表示前 \(i\) 个物品、背包剩余容量为 \(w\) 时的最大总价值。 -
状态转移方程:
- 初始条件:
\(V(0, w) = 0\),表示没有物品时的价值为0。
该算法时间复杂度为 \(O(nW)\),广泛用于资源分配、项目选择等问题。
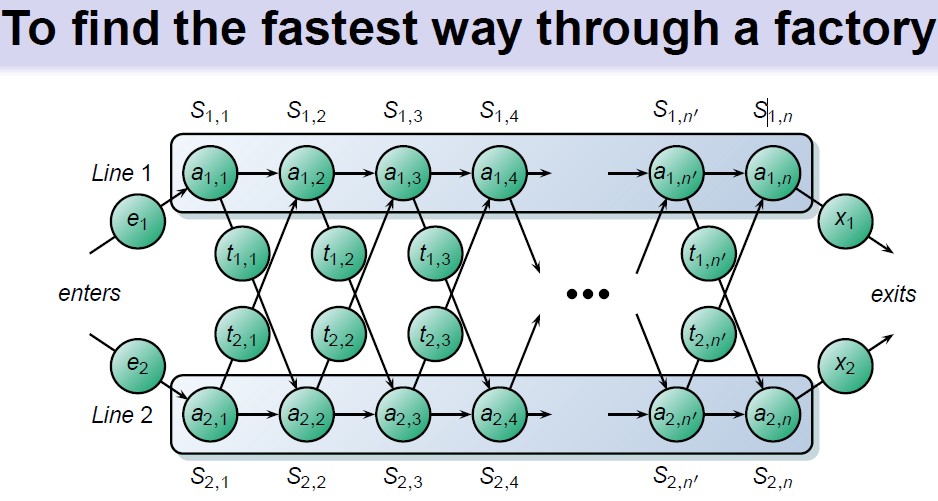
5.2 最短路径问题(Shortest Path Problem)
问题描述:
在一个有向图中,已知每条边的权重,求从源点 \(s\) 到目标点 \(t\) 的最短路径长度。
动态规划思路:
- 将图结构转化为多阶段图(如 DAG)。
- 状态为当前所在节点,动作为选择通向下一节点的边。
- 状态转移方程为:
其中 \(d_{ij}\) 表示从节点 \(i\) 到 \(j\) 的距离。
经典算法如 Bellman-Ford、Dijkstra 实质上是动态规划的不同实现形式。
5.3 库存控制模型(Inventory Control)
问题描述:
设有 \(T\) 个销售周期,每期有需求 \(d_t\),库存初始为 \(s_0\),每次订货有固定成本、单位成本、持有成本与缺货惩罚,求最优订货策略使总成本最小。
动态规划建模:
- 状态:库存水平 \(s_t\)
- 动作:每期订货量 \(a_t\)
- 状态转移:
- 递推公式:
这些些问题的共同点在于:
- 拥有清晰的状态定义和递推结构;
- 满足“最优子结构”性质;
- 子问题重复性强,适合自底向上递推或自顶向下记忆化搜索。
因此,动态规划成为解决此类问题的首选方法。
六、贝尔曼的学术贡献与社会影响
理查德·贝尔曼(Richard Bellman)不仅是动态规划的创始人,更是现代多阶段决策理论的奠基者。他的学术贡献深远,影响跨越数学、工程、计算机科学乃至社会科学领域。
📘 6.1 理论开创:建立动态规划数学体系
贝尔曼在1950年代提出“动态规划”(Dynamic Programming)这一理论框架,首次系统地解决了多阶段决策问题。他提出的贝尔曼最优性原理,通过将问题划分为子问题递归求解,极大拓展了运筹学的边界。
贝尔曼方程的提出,将多阶段优化问题转化为具有递归结构的数学表达,使得原本复杂的全局优化问题变得可解和可编程,为之后的算法发展奠定基础。
🔁 6.2 控制论基础:现代控制理论的核心支柱
动态规划在最优控制问题中具有核心地位。无论是连续时间系统中的Hamilton-Jacobi-Bellman(HJB)方程,还是离散时间下的价值函数方法,均可追溯到贝尔曼的思想。
他的理论被广泛应用于火箭轨道设计、导弹追踪、机器人路径规划等场景,是现代航天控制系统的理论支柱。
🤖 6.3 影响计算机科学:AI与强化学习的基石
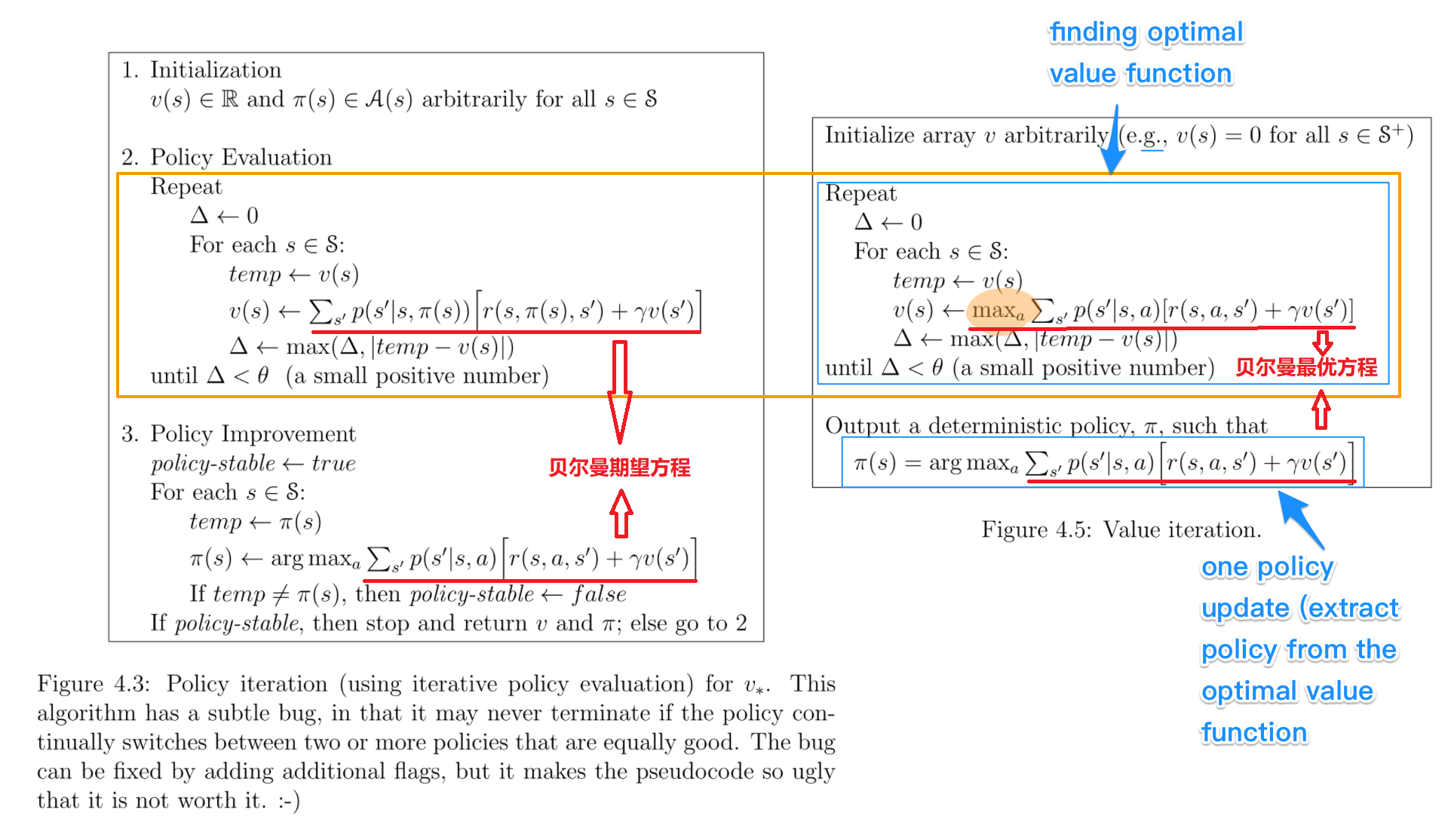
在人工智能领域,贝尔曼方程是强化学习中最基础的结构,价值迭代(Value Iteration)与策略迭代(Policy Iteration)均直接依赖其原理。
例如,Q-learning 算法的核心更新规则就是贝尔曼期望方程的一个无模型实现。在 AlphaGo 的策略评估和更新过程中,也蕴含着贝尔曼的思想。
🧑🏫 6.4 教育与传播:推动跨学科融合
贝尔曼一生发表了超过600篇论文、编写了39本专著,涵盖数学、生物医学、计算机、统计、控制等多个学科。他提倡将复杂系统建模与简化求解结合,强调跨学科的重要性。
他培养了大量后继学者,其学生遍布控制、运筹、AI 等领域,成为推动现代工程科学发展的重要力量。
🌍 6.5 实践应用与社会影响
贝尔曼的理论不仅存在于数学公式中,更广泛应用于现实世界:
- 在物流与运输优化中,用于制定动态配送策略;
- 在金融投资决策中,用于多期资产配置;
- 在医疗管理中,优化治疗过程与资源配置;
- 在智能制造中,实现多阶段工艺控制与调度。
他的理论成为政府、企业、军事、医疗等领域解决高复杂度问题的重要工具。
贝尔曼因其卓越成就获得美国国家科学奖章、IEEE控制领域终身成就奖等多项殊荣。他不仅是一个理论开创者,更是将数学智慧注入现实世界的实践先行者。正如他自己所说:
“科学不是为了解释复杂事物,而是为了用简单方法做出最优决策。”
他无疑是现代优化理论、控制论与智能决策科学的开山巨擘。
七、未来展望:动态规划在智能时代的价值与挑战
进入大数据与人工智能高速发展的时代,动态规划依然是解决复杂系统决策问题的基石之一。在智能化决策系统中,贝尔曼方程已成为强化学习的数理基础,被广泛用于Q-learning、策略迭代、价值迭代等算法,推动了AlphaGo、ChatGPT等智能系统的崛起。
随着算力的提升和数据资源的积累,动态规划逐渐突破传统局限,在大规模优化问题中展现出更强能力。例如,在电网调度、城市交通调控、资源分配优化等领域,DP算法通过并行计算和近似方法实现实时决策。
但挑战依然严峻。状态空间爆炸问题导致传统动态规划在高维场景下计算量急剧上升。为此,学界发展出近似动态规划(ADP)、**深度强化学习(DRL)**等方法,通过神经网络表示状态值函数,实现了从“表格化”到“函数逼近”的跃迁。
未来,动态规划将继续与机器学习、分布式计算、云边协同等技术融合,助力解决跨阶段、不确定、复杂动态环境中的决策优化问题,成为智能制造、智慧医疗、智慧城市、自动驾驶等新兴领域的重要算法支撑。贝尔曼的思想将持续照亮“智能决策”的未来之路。
八、总结:贝尔曼与动态规划的时代价值
理查德·贝尔曼不仅是一位卓越的数学家,更是一位划时代的思想家。他提出的动态规划理论,成功打破了传统最优化方法在多阶段、时序决策问题中的瓶颈,为运筹学、控制论和人工智能奠定了坚实的数学基础。
贝尔曼提出的“最优性原理”不仅具有数学美感,更具有强大生命力,使得复杂系统得以分解为若干子问题逐步求解,大幅提高了解决问题的效率与可行性。其思想已经深入强化学习、智能控制、资源调度、图像识别等众多领域。
在今天的智能时代,动态规划仍以多种形式活跃在科研与工程实践中。无论是自动驾驶决策路径,还是智能制造的资源分配,又或是城市交通的智能调度,贝尔曼的理论都在发挥着无可替代的作用。他留下的不只是一个算法,更是一种贯穿时间与空间的决策思维方式,必将在未来智能系统的构建中持续释放巨大价值。
九、参考文献
- Bellman, R. (1957). Dynamic Programming. Princeton University Press.
- Bertsekas, D. P. (2017). Dynamic Programming and Optimal Control. Athena Scientific.
- Puterman, M. L. (2014). Markov Decision Processes: Discrete Stochastic Dynamic Programming. Wiley.
- Sutton, R. S., & Barto, A. G. (2018). Reinforcement Learning: An Introduction. MIT Press.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号