统计学复习——思维导图与知识点汇总
目录
统计数据的可视化
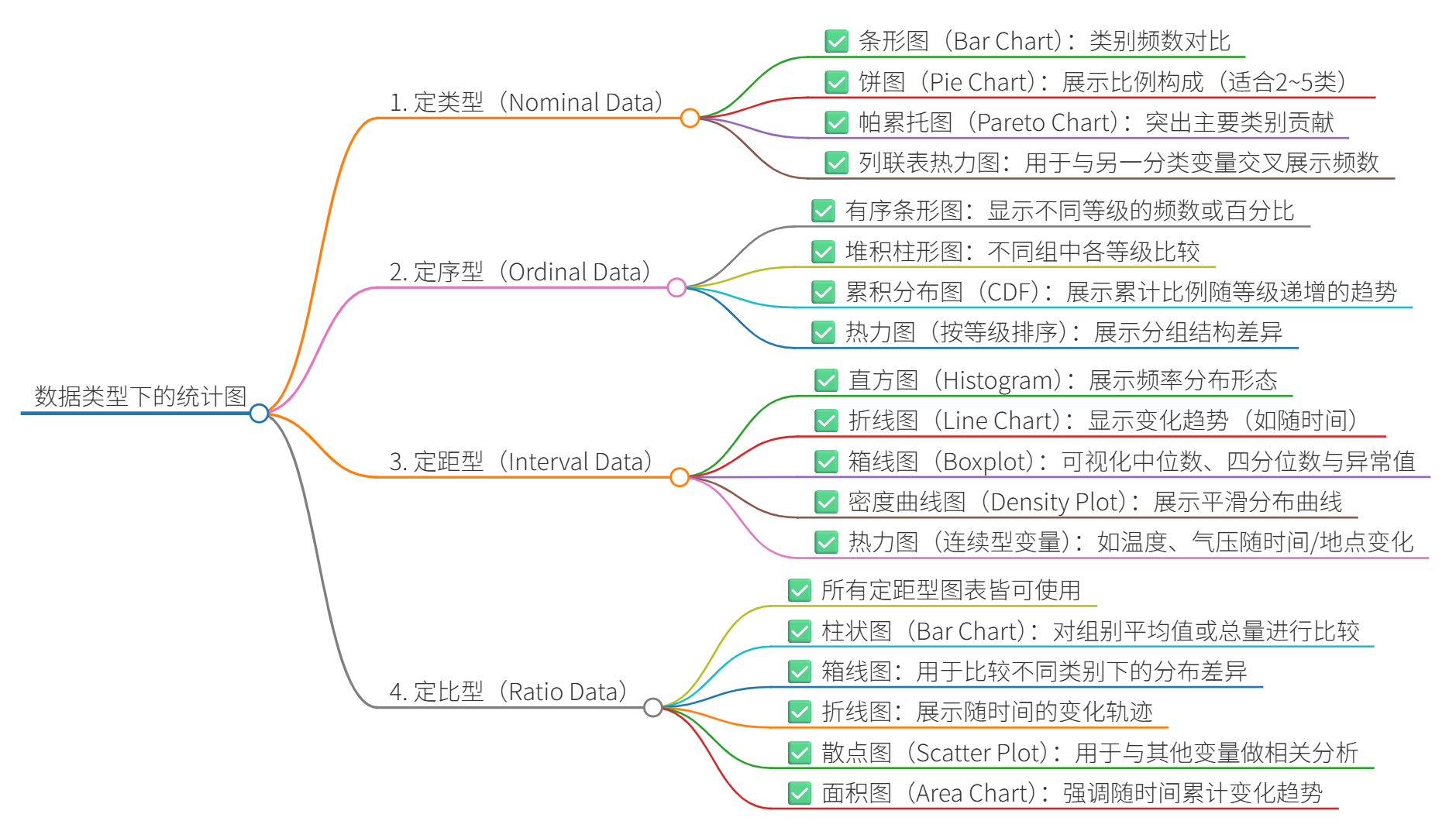
在统计分析与数据可视化过程中,数据类型的识别与图表类型的选择密切相关。选择合适的统计图不仅能清晰传达信息,还能避免误导。因此,我们应根据变量的尺度类型(如定类、定序、定距、定比)与分析目的(如分布、比较、关联)进行合理匹配。
定类变量(Nominal)
定类变量仅用于分类,类别间无顺序关系,如性别、地区、血型等。
| 可视化目的 | 常用图表 | 特点 |
|---|---|---|
| 分布展示 | 条形图(Bar Chart) | 水平或垂直条形表示类别频数 |
| 构成分析 | 饼图(Pie Chart) | 展示各类占总体比例(慎用) |
| 频率排序 | 帕累托图(Pareto Chart) | 条形图+累计线,突出主要项 |
✅ 提示:条形图更具比较优势,饼图仅用于类别数较少且总量对比明确的情况。
定序变量(Ordinal)
定序变量有明确顺序,但间距不确定,如满意度等级(非常满意 → 一般 → 不满意)、教育程度等。
| 可视化目的 | 常用图表 | 特点 |
|---|---|---|
| 顺序频率 | 条形图(排序) | 横轴按等级顺序排列,直观反映变化趋势 |
| 分布比例 | 堆积柱图 | 各等级比例并排比较 |
| 单变量累计 | 累积分布图(CDF) | 反映累计频率趋势,适合调查等级结果 |
✅ 提示:可视化时应保持等级顺序,避免按字母排序造成误解。
定距变量(Interval)
定距变量具有固定间距但无绝对零点,如温度(℃)、时间等。
| 可视化目的 | 常用图表 | 特点 |
|---|---|---|
| 分布形态 | 直方图(Histogram) | 连续区间分组,适合查看集中趋势与偏态 |
| 离散波动 | 折线图(Line Chart) | 显示趋势变化,常用于时间序列数据 |
| 离群值识别 | 箱线图(Boxplot) | 可视化中位数、四分位数与异常值 |
✅ 提示:直方图用于数值型变量频率展示,区分于条形图(类别型);折线图强调趋势,适用于顺序连续观测。
定比变量(Ratio)
定比变量有绝对零点,具备“倍数”意义,如收入、年龄、身高、销售额等,是最常用的数量型数据。
| 可视化目的 | 常用图表 | 特点 |
|---|---|---|
| 分布概貌 | 直方图、密度图 | 反映数据集中趋势与尾部特征 |
| 分类比较 | 箱线图、柱状图 | 横向比较不同组别的中心位置和离散程度 |
| 变化趋势 | 折线图、面积图 | 用于描述随时间或指标变化的轨迹 |
✅ 提示:如数据偏态严重,建议结合箱线图或对数坐标进一步探究。
数据的概括性度量
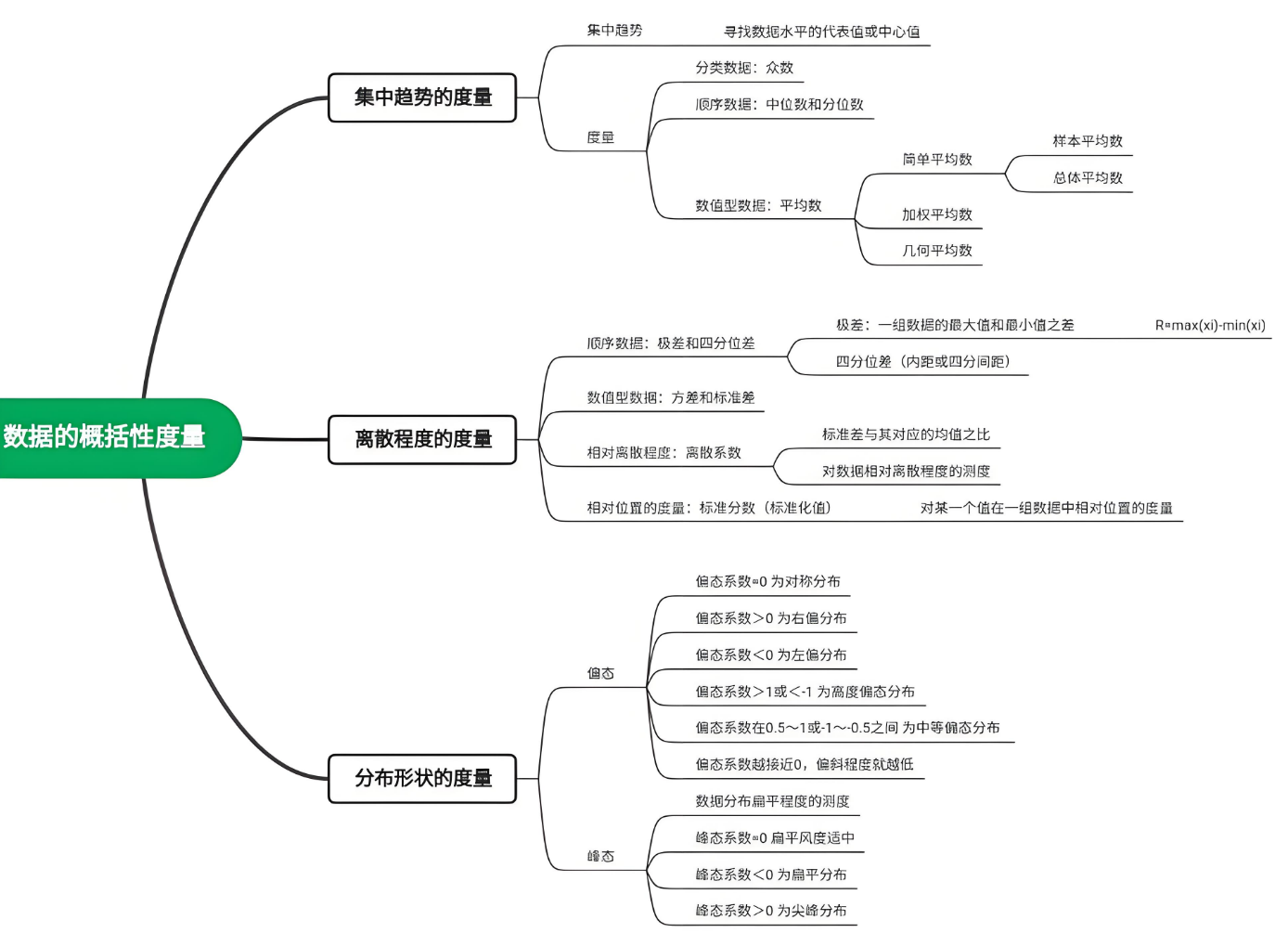
集中趋势的度量
- 众数(mode):一组数据中出现次数最多的变量(EXCEL函数:
MODE(number1,number2,……))。 - 中位数(median):一组数据排序后处于中间位置上的变量,中位数位置=(n+1)/2(EXCEL函数:
MEDIAN(number1,number2,……))。 - 四分位数(quartile):一组数据排序后处于25%和75%位置上的值,位置分别为:
- QL位置=\(\frac{n}{4}\)
- QU位置=\(\frac{3n}{4}\)(EXCEL函数:
QUARTILE(array,quart))。
- 平均数(mean):一组数据相加后除以数据个数得到的结果。
- 简单平均数(simple mean):\(\overline{x}=\frac{\sum_{i=0}^{n} x_i}{n}\)
- 加权平均数(weighted mean):\(\overline{x}=\frac{\sum_{i=0}^{n} M_i f_i}{n}\)(权重与频数的乘积)
- 几何平均数(geometric mean):(EXCEL函数:
GEOMEAN(number1,number2,……))
离散趋势的度量
- 异众比率(variation ratio):值非众数组的频数占总频数的比例。(\(V_r=1-\frac{f_m}{N}\),其中\(N\)为变量值的总频数,\(f_m\)为众数组的频数)
- 四分位差(quartile deviation):也称内距或四分位距,它是上四分位分数与下四分位分数之差。
- 方差(variance):各变量值预期平均数离差平方的平均数。
- 标准差(standard deviation):方差的平方根。
- 离散系数(coefficient of variation):一组数据的标准差与其相应的平均数之比。
偏态与峰态的度量
- 偏态(skewness):它是对数据分布对称性的测度。
- 偏态系数(coefficient of skewness):它是样本标准差的三次方。(EXCEL函数:
SKEW(number1,number2,……),样本数少于3个或者标准差为0,则返回错误值#DIV/0!)- 偏态的强度:
- 偏态系数=0,数据的分布是对称的;
- 偏态系数>1或者<-1,高度偏态分布;
- 偏态系数位于\(0.5,1\)或者\(-1,-0.5\),中等偏态分布。
- 偏态的方向判断:
- SK为正值时,正离差值较大,正偏或者右偏;
- SK为负值时,负离差值较大,负偏或者左偏。
- 偏态的强度:
- 峰态(kurtosis):它是对数据分布平峰或尖峰程度的测度。
- 峰态系数(coefficient of kurtosis):它是样本标准差的四次方。(EXCEL函数:
KURT(number1,number2,……),样本数少于4个或者标准差为0,则返回错误值#DIV/0!)- 峰态的测度:
- K=0,正态分布;
- K>0,尖峰分布,数据的分布更集中;
- K<0,扁平分布,数据的分布更分散。
- 峰态的测度:
统计量及其抽样分布
统计量(statistic)是由样本数据计算得出的函数,例如样本均值、样本方差、样本比例等。由于样本具有随机性,统计量本身也是随机变量,其分布被称为抽样分布(sampling distribution)。抽样分布是参数估计、假设检验等统计推断的基础。
统计学四大常用分布
统计学中最基础且常用于抽样分布理论构建的四大分布如下:
| 分布名称 | 记号 | 应用场景 | 特点 |
|---|---|---|---|
| 正态分布 | \(N(\mu, \sigma^2)\) | 样本均值分布、大样本近似分布 | 连续型分布,钟形对称,参数为均值和方差 |
| t 分布 | \(t_{df}\) | 样本容量较小时均值估计所用分布(总体方差未知) | 比正态分布尾部更厚,依赖自由度 |
| 卡方分布 | \(\chi^2_k\) | 用于方差检验、拟合优度检验、构建样本方差分布 | 非对称分布,由正态平方和构成 |
| F 分布 | \(F_{d_1,d_2}\) | 两个样本方差比值的分布,用于方差齐性检验、方差分析(ANOVA) | 由两个卡方分布的比值构成 |
抽样分布定理
抽样分布定理揭示了样本统计量在重复抽样下的概率分布特征,是理解估计误差和构造置信区间的理论基础。
设 \(X\) 为正态分布,其均值为 \(\mu\),方差为 \(\sigma^2\),从中抽取容量为 \(n\) 的简单随机样本\(\{X_1, X_2, \dots, X_n\}\),定义如下统计量:
- 样本均值:\(\bar{X} = \frac{1}{n} \sum_{i=1}^n X_i\)
- 样本方差:\(S^2 = \frac{1}{n-1} \sum_{i=1}^n (X_i - \bar{X})^2\)
则有以下结论:
(1)样本均值的抽样分布:
(2)样本方差的抽样分布:
该结果说明:样本方差乘以自由度后除以总体方差,服从自由度为 \(n-1\) 的卡方分布。
中心极限定理(CLT)
中心极限定理(Central Limit Theorem)指出,无论原始总体分布是否为正态分布,只要样本容量足够大,样本均值的标准化变量就趋近于标准正态分布:
这是抽样分布理论中最重要的近似依据,为非正态总体提供了正态推断的可能,使得我们可以使用 z 检验、构造近似置信区间等。
参数估计

一个总体参数的区间估计
- 总体均值的区间估计:
| 总体分布 | 样本量 | σ已知 | 区间估计公式 | σ未知 | 区间估计公式 |
|---|---|---|---|---|---|
| 正态分布 | 大样本(\(n \geq 30\)) | ✔️ | \(\bar{X} \pm z_{\alpha/2} \cdot \dfrac{\sigma}{\sqrt{n}}\) | ✔️ | $\bar{X} \pm z_{\alpha/2} \cdot \dfrac{s}{\sqrt{n}}$ |
| 正态分布 | 小样本(\(n < 30\)) | ✔️ | \(\bar{X} \pm z_{\alpha/2} \cdot \dfrac{\sigma}{\sqrt{n}}\) | ✔️ | $\bar{X} \pm t_{\alpha/2}(n-1) \cdot \dfrac{s}{\sqrt{n}}$ |
| 非正态分布 | 大样本(\(n \geq 30\)) | ✔️ | \(\bar{X} \pm z_{\alpha/2} \cdot \dfrac{\sigma}{\sqrt{n}}\) (依中心极限定理) | ✔️ | \(\bar{X} \pm z_{\alpha/2} \cdot \dfrac{s}{\sqrt{n}}\) (依中心极限定理) |
- 总体比例的区间估计
| 样本量 | 点估计 | 区间估计公式 | 适用条件 |
|---|---|---|---|
| 大样本(\(n \geq 30\)) | \(\hat{p} = \dfrac{x}{n}\) | \(\hat{p} \pm z_{\alpha/2} \cdot \sqrt{ \dfrac{\hat{p}(1 - \hat{p})}{n} }\) | \(n\hat{p} \geq 5; n(1 - \hat{p}) \geq 5\)(正态近似) |
- 总体方差的区间估计
| 总体分布 | 样本量 | 区间估计公式 | 适用分布 | 条件 |
|---|---|---|---|---|
| 正态分布 | 任意样本量 | \(\left( \dfrac{(n-1)s^2}{\chi^2_{1 - \alpha/2}}, \dfrac{(n-1)s^2}{\chi^2_{\alpha/2}} \right)\) | \(\chi^2(n-1)\) 分布 | 总体服从正态分布 |
两个总体参数的区间估计
- 两个总体均值之差的区间估计
| 参数 | 点估计量(值) | 标准误差 | (1-α)%的置信区间 | 假定条件 |
|---|---|---|---|---|
| 两个总体均值之差 | \(\bar{X}_1 - \bar{X}_2\) | \(\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}\) | \((\bar{X}_1 - \bar{X}_2) \pm z_{\alpha/2} \cdot \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}\) | (1)独立大样本(\(n_1 \geq 30, n_2 \geq 30\)) (2)\(\sigma_1, \sigma_2\) 已知 |
| 两个总体均值之差 | \(\bar{X}_1 - \bar{X}_2\) | \(\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}\) | \((\bar{X}_1 - \bar{X}_2) \pm z_{\alpha/2} \cdot \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}\) | (1)独立大样本(\(n_1 \geq 30, n_2 \geq 30\)) (2)\(\sigma_1, \sigma_2\) 未知 |
| 两个总体均值之差 | \(\bar{X}_1 - \bar{X}_2\) | \(s_p \cdot \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}\),其中 \(s_p^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1 + n_2 - 2}\) | \((\bar{X}_1 - \bar{X}_2) \pm t_{\alpha/2}(n_1 + n_2 - 2) \cdot s_p \cdot \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}\) | (1)两个正态总体 (2)独立小样本(\(n_1 < 30, n_2 < 30\)) (3)\(\sigma_1, \sigma_2\) 未知但相等 |
| 两个总体均值之差 | \(\bar{X}_1 - \bar{X}_2\) | \(\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}\) | \((\bar{X}_1 - \bar{X}_2) \pm t_{\alpha/2}(\nu) \cdot \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}\),\(\nu\)由Satterthwaite近似自由度确定 | (1)两个正态总体 (2)独立小样本(\(n_1 < 30, n_2 < 30\)) (3)$\sigma_1, \sigma_2$ 未知且不相等 |
| 两个总体均值之差 | \(\bar{d}\)(差值的平均) | \(\frac{s_d}{\sqrt{n}}\) | \(\bar{d} \pm z_{\alpha/2} \cdot \frac{s_d}{\sqrt{n}}\) | 匹配大样本(\(n_1 = n_2 \geq 30\)) |
| 两个总体均值之差 | \(\bar{d}\) | \(\frac{s_d}{\sqrt{n}}\) | \(\bar{d} \pm t_{\alpha/2}(n - 1) \cdot \frac{s_d}{\sqrt{n}}\) | (1)两个正态总体 (2)匹配小样本(\(n_1 = n_2 < 30\)) |
- 两个总体比例之差的区间估计
| 参数 | 点估计量(值) | 标准误差 | (1-α)%的置信区间 | 假定条件 |
|---|---|---|---|---|
| 两个总体比例之差 | $\hat{p}_1 - \hat{p}_2$ | \(\sqrt{\frac{\hat{p}_1(1 - \hat{p}_1)}{n_1} + \frac{\hat{p}_2(1 - \hat{p}_2)}{n_2}}\) | \((\hat{p}_1 - \hat{p}*2) \pm z*{\alpha/2} \cdot \sqrt{\frac{\hat{p}_1(1 - \hat{p}_1)}{n_1} + \frac{\hat{p}_2(1 - \hat{p}_2)}{n_2}}\) | (1)两个二项总体 (2)匹配小样本(\(n_1<30,n_2<30\)) (3)正态近似适用:\(n_1\hat{p}_1;n_1(1-\hat{p}_1);n_2\hat{p}_2;n_2(1-\hat{p}_2) \geq 5\) |
- 两个总体方差比的区间估计
| 参数 | 点估计量(值) | 标准误差 | (1-α)%的置信区间 | 假定条件 |
|---|---|---|---|---|
| 两个总体方差比 \(\dfrac{\sigma_1^2}{\sigma_2^2}\) | \(\dfrac{s_1^2}{s_2^2}\) | (不要求) | \(\left( \dfrac{s_1^2}{s_2^2} \cdot \dfrac{1}{F_{1 - \alpha/2}(n_1 - 1, n_2 - 1)}, \dfrac{s_1^2}{s_2^2} \cdot \dfrac{1}{F_{\alpha/2}(n_1 - 1, n_2 - 1)} \right)\) | 两个正态总体 |
样本量的确定
- 估计总体均值时样本量的确定
由于估计误差\(E=z_{\alpha/2}\frac{\sigma}{\sqrt{n}}\),因此可以推断出确认样本量的公式如下:
- 估计总体比例时样本量的确定
由估计误差\(E=z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\)可以推导出重复抽样或无限总体抽样条件下确认样本量的公式如下:
假设检验
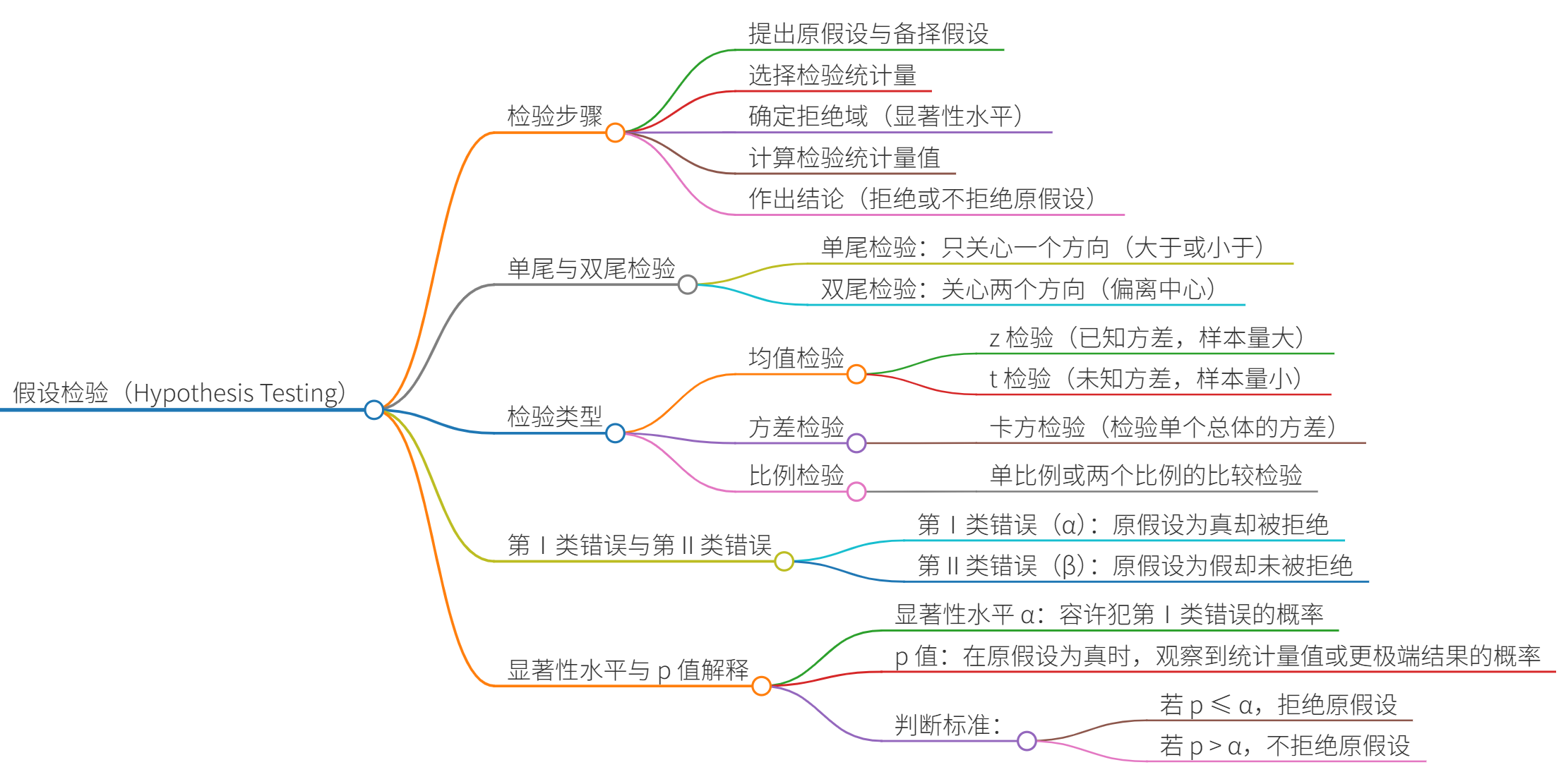
两类错误
| 项目 | 没有拒绝 | 拒绝 |
|---|---|---|
| \(H_0\)为真 | 1-α(正确决策) | β(弃真错误) |
| \(H_0\)为伪 | α(取伪错误) | (正确决策) |
一个总体参数的检验
在一个总体参数的检验中,用到的检验统计量主要有三个:Z统计量,t统计量,χ²统计量。Z统计量和t统计量主要用于均值和比例的检验,χ²统计量则用于方差的检验。
| 检验参数 | 条件要素 | 检验统计量 |
|---|---|---|
| 总体均值检验 | 大样本 | \(Z=\frac{\overline{x}-\mu}{\sigma/\sqrt{n}}\) |
| 总体均值检验 | 小样本(σ已知) | \(Z=\frac{\overline{x}-\mu}{\sigma/\sqrt{n}}\) |
| 总体均值检验 | 小样本(σ未知) | \(t=\frac{\overline{x}-\mu}{s/\sqrt{n}}\) |
| 总体比例检验 | 大样本 | \(Z=\frac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\) |
| 总体方差检验 | 大样本 | \(\chi^2=\frac{(n-1)s^2}{\sigma^2}\) |
两个总体参数的检验
| 检验参数 | 条件要素 | 检验统计量 |
|---|---|---|
| 均值之差检验 | 样本量大 σ²已知或未知 |
\(Z=\frac{(\overline{x}_1-\overline{x}_2)-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}\) |
| 均值之差检验 | 样本量小 σ²未知,且\(\sigma_1^2=\sigma_2^2\) |
\(t=\frac{(\overline{x}_1-\overline{x}_2)-(\mu_1-\mu_2)}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\) |
| 均值之差检验 | 样本量小 σ²未知,且\(\sigma_1^2\neq\sigma_2^2\) |
\(t=\frac{(\overline{x}_1-\overline{x}_2)-(\mu_1-\mu_2)}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}\) |
| 比例之差检验 | 服从二项分布 | \(Z=\frac{(\hat{p}_1-\hat{p}_2)-(p_1-p_2)}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}}\) |
| 方差比检验 | 两个正态总体 | \(F=\frac{s_1^2}{s_2^2}\) |
方差分析
单因素方差分析
- 总平方和(sum of squares for total):\(SST=\sum_{i=1}^{k}\sum_{j=1}^{n_i}(x_{ij}-\overline{x})^2\)
- 组间平方和(sum of squares for factor A):\(SSA=\sum_{i=1}^{k}n_i(\overline{x}_i-\overline{x})^2\)
- 组内平方和(sum of squares for error):\(SSE=SST-SSA\)
EXCEL方差分析表:
| 误差来源 | 平方和SS | 自由度df | 均方MS | F值 | P值 | F临界值 |
|---|---|---|---|---|---|---|
| 组间(因素影响) | SSA | k-1 | MSA | MSA/MSE | ||
| 组内(误差) | SSE | n-k | MSE | |||
| 总和 | SST | n-1 |
表格分析:
- 若F值>F临界值,则拒绝原假设,表明有显著差异;
- 若F值<F临界值,则不拒绝原假设,表明没有显著差异;
- 若P<α,则拒绝\(H_0\),若P>α,则不拒绝\(H_0\)。
双因素方差分析
| 误差来源 | 平方和SS | 自由度df | 均方MS | F值 | P值 | F临界值 |
|---|---|---|---|---|---|---|
| 行因素 | SSR | k-1 | MSR | |||
| 列因素 | SSC | n-k | MSC | |||
| 误差 | SSE | (k-1)*(r-1) | MSE | |||
| 总和 | SST | kr-1 |
表格分析:
- 若\(F_{行}>F_{临界值}\),拒绝原假设,表明行之间有显著差异,反之则不拒绝原假设,表明行之间没有明显差异;
- 若\(F_{列}>F_{临界值}\),拒绝原假设,表明列之间有显著差异,反之则不拒绝原假设,表明列之间没有明显差异;
- 如果P-value<α,拒绝\(H_0\),P-value>α,不拒绝\(H_0\)。
有交互作用的双因素方差分析
EXCEL方差分析表:
| 误差来源 | 平方和SS | 自由度df | 均方MS | F值 | P值 | F临界值 |
|---|---|---|---|---|---|---|
| 行因素 | SSR | k-1 | MSR | |||
| 列因素 | SSC | n-k | MSC | |||
| 交互作用 | SSRC | (k-1)*(r-1) | MSRC | |||
| 误差 | SSE | kr(m-1) | MSE | |||
| 总和 | SST | kr-1 |
表格分析:
- 行因素的P-value<α,则拒绝原假设,表明行之间有显著差异,反之,不拒绝原假设,表明行之间没有显著差异;
- 列因素的P-value<α,则拒绝原假设,表明列之间有显著差异,反之,不拒绝原假设,表明列之间没有显著差异;
- 交互作用的P-value<α,则拒绝原假设,表明相互作用有显著影响,反之,不拒绝原假设,表明相互作用没有显著影响。
一元线性回归
- 相关系数(correlation coefficient):根据样本数据计算的度量两个变量之间线性关系强度的统计量(EXCEL函数:
CORREL(Array1,Array2))。
EXCEL一元线性回归表:
| 回归统计 | |
|---|---|
| Multiple R | |
| R Square | |
| Adjusted R Square | |
| 标准误差 | |
| 观测值 | n |
方差分析
| SS | df | MS | F值 | P值 | Significance F | |
|---|---|---|---|---|---|---|
| 回归 | SSA | k-1 | MSA | MSA/MSE | ||
| 残差 | SSE | n-k | MSE | |||
| 总计 | SST | n-1 |
| Coefficients | 标准误差 | t Stat | P-value | Lowe 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intercept | ||||||
| X Variable 1 |
表分析:
- 回归方程:\(y=\hat{\beta}_0+\hat{\beta}_1x\);
- r=1时,x与y之间为完全正线性相关关系,r=-1时,x与y之间为完全负线性相关关系;r区间为(0,1)时,x与y之间为正线性相关关系,r区间为(-1,0)时,x与y之间为负线性相关关系。
- \(R^2\)的值表明x与y之间的拟合强度,\(R^2\)的值越接近1,表明x与y相关性越强,拟合性越好。
- 标准误差可以用来度量各实际观测点在直线周围散布状况的一个统计量,说明判断结果的误差范围。
- 线性关系检验:若\(F>F_{临界值}\),拒绝\(H_0\),表明两个变量之间的线性关系是显著的;若\(F<F_{临界值}\),不拒绝\(H_0\),没有证据表明两个变量之间的线性关系显著(除此之外,还需要判断P值与α之间的大小以确定是否拒绝\(H_0\),EXCEL表中的显著性F(Significance F)就是用于检验的P值)。
- 回归系数的检验:\(t(t Stat)>t_{临界值}\),拒绝原假设,表明该变量是显著性影响要素(判断P值方法与前面相同)。
- 点估计:代入自变量到回归方程获得相应的因变量。
- 置信区间估计:\(\hat{y}\pm t_{\alpha/2}s_{\hat{y}}\)
- 预测区间估计:\(\hat{y}\pm t_{\alpha/2}s_{pred}\),预测区间要比置信区间更宽一些。
多元线性回归
EXCEL多元线性回归表:
| 回归统计 | |
|---|---|
| Multiple R | |
| R Square | |
| Adjusted R Square | |
| 标准误差 | |
| 观测值 | n |
方差分析
| SS | df | MS | F值 | P值 | Significance F | |
|---|---|---|---|---|---|---|
| 回归 | SSA | k-1 | MSA | MSA/MSE | ||
| 残差 | SSE | n-k | MSE | |||
| 总计 | SST | n-1 |
| Coefficients | 标准误差 | t Stat | P-value | Lowe 95% | Upper 95% | |
|---|---|---|---|---|---|---|
| Intercept | ||||||
| X Variable 1 | ||||||
| X Variable 2 | ||||||
| X Variable 3 | ||||||
| …… | …… |
表分析:
- 回归方程:\(y=\hat{\beta}_0+\hat{\beta}_1x_1+\hat{\beta}_2x_2+\cdots+\hat{\beta}_kx_k\);
- r=1时,x与y之间为完全正线性相关关系,r=-1时,x与y之间为完全负线性相关关系;r区间为(0,1)时,x与y之间为正线性相关关系,r区间为(-1,0)时,x与y之间为负线性相关关系。
- \(R^2_{adj}\)为调整多重判定系数,表明x与y之间的拟合强度,\(R^2_{adj}\)的值越接近1,表明x与y相关性越强,拟合性越好。
- 标准误差可以用来度量各实际观测点在直线周围散布状况的一个统计量,说明判断结果的误差范围。
- 线性关系检验:若\(F>F_{临界值}\),拒绝\(H_0\),表明两个变量之间的线性关系是显著的;若\(F<F_{临界值}\),不拒绝\(H_0\),没有证据表明两个变量之间的线性关系显著(除此之外,还需要判断P值与α之间的大小以确定是否拒绝\(H_0\),EXCEL表中的显著性F(Significance F)就是用于检验的P值)。
- 回归系数的检验:\(t(t Stat)>t_{临界值}\),拒绝原假设,表明该变量是显著性影响要素(判断P值方法与前面相同)。
时间序列分析与预测
时间序列分析是一类针对按时间顺序排列的数据所进行的统计建模与预测方法,广泛应用于经济、金融、市场、气象等领域。时间序列的主要目的是理解数据的结构特征,并对未来进行科学预测。
时间序列的组成
一个典型的时间序列通常由以下四个部分构成:
- 趋势(Trend):长期方向性变动,如经济增长、温度上升;
- 季节(Seasonal):在固定时间周期内重复出现的模式,如季度销售、节日波动;
- 周期(Cyclical):非固定周期的波动,一般与宏观经济周期相关;
- 随机项(Random/Irregular):无法解释的非系统性波动,是纯粹的噪声。
对这些成分的分离和识别,有助于后续模型选择和预测。
平稳性检验
时间序列模型(如ARMA、ARIMA)对数据的平稳性要求较高,平稳序列意味着其均值、方差、协方差不随时间变化。常用检验方法为ADF检验(Augmented Dickey-Fuller Test),其原假设为序列存在单位根(即非平稳),若检验结果显著,则拒绝原假设,说明序列平稳。
对非平稳序列,常需通过差分转化为平稳序列。
ACF与PACF图
- 自相关函数(ACF):衡量序列与其滞后值之间的整体线性相关性;
- 偏自相关函数(PACF):剔除中间滞后变量的影响,仅保留直接滞后项影响。
ACF/PACF图是识别AR(自回归)、MA(移动平均)模型阶数的重要工具。例如:
- ACF尾减、PACF截尾:可能为AR模型;
- ACF截尾、PACF尾减:可能为MA模型;
- ACF和PACF尾减:考虑ARMA模型。
模型类型
- AR(自回归模型):序列当前值由其过去若干值加误差项决定;
- MA(移动平均模型):序列当前值由过去误差项的加权平均决定;
- ARMA(自回归-移动平均模型):综合上述两者,要求序列平稳;
- ARIMA(差分自回归移动平均模型):适用于非平稳序列,通过差分使其平稳后再建模;
- 指数平滑法:适用于趋势和季节性较弱的数据,常见方法如SES(简单指数平滑)、Holt线性法、Holt-Winters季节法等。
统计指数
统计指数用于反映某类现象在不同时期或地区之间的变动程度,是经济统计分析中重要的工具。
简单综合指数
- 不考虑权重,适用于指标数量较少、单位一致的情况。
- 常用形式:
- \(P_0Q_0\) 和 \(P_1Q_1\)
- \(P\):质量指标(如价格、工资等)
- \(Q\):数量指标(如产量、人数等)
- \(P_0\)、\(P_1\):基期与报告期质量指标指数
- \(Q_0\)、\(Q_1\):基期与报告期数量指标指数
- \(P_0Q_0\) 和 \(P_1Q_1\)
- 特点:
- 计算简便
- 忽略指标重要性差异,实际应用有限
加权综合指数
通过引入权数 \(w\),反映各组成部分的重要性,使结果更科学。
拉氏指数(Laspeyres Index)
- 使用基期数量 \(Q_0\)作为权数
- 价格指数公式:\[I_L = \frac{\sum P_1 Q_0}{\sum P_0 Q_0} \]
- 特点:
- 能反映价格变动趋势
- 可能高估物价上涨影响
帕氏指数(Paasche Index)
- 使用报告期数量 \(Q_1\)作为权数
- 价格指数公式:\[I_P = \frac{\sum P_1 Q_1}{\sum P_0 Q_1} \]
- 特点:
- 更能体现实际结构变化
- 需报告期数据,计算复杂



 浙公网安备 33010602011771号
浙公网安备 33010602011771号