Myerson值——网络博弈中的公平分配(Sharpley值的进化)
在现实生活中,很多合作活动并不是完全自由进行的,而是受到关系网络、地理位置或通信结构的限制。例如,企业之间的合作依赖合同关系,社交平台中的信息传播依赖好友关系,科研合作依赖学术联系。这些网络结构限制了玩家之间的协作方式,使得传统的合作博弈理论——尤其是Shapley值——在解释和分配联合收益时显得力不从心。为了解决这一问题,Roger Myerson 在1977年提出了迈尔森值(Myerson Value),将网络结构引入合作博弈的分析中,为“受限合作”提供了一种公平分配机制。迈尔森值不仅保留了Shapley值的公平性原则,还结合图结构的可达性特征,使分配结果更加契合实际。
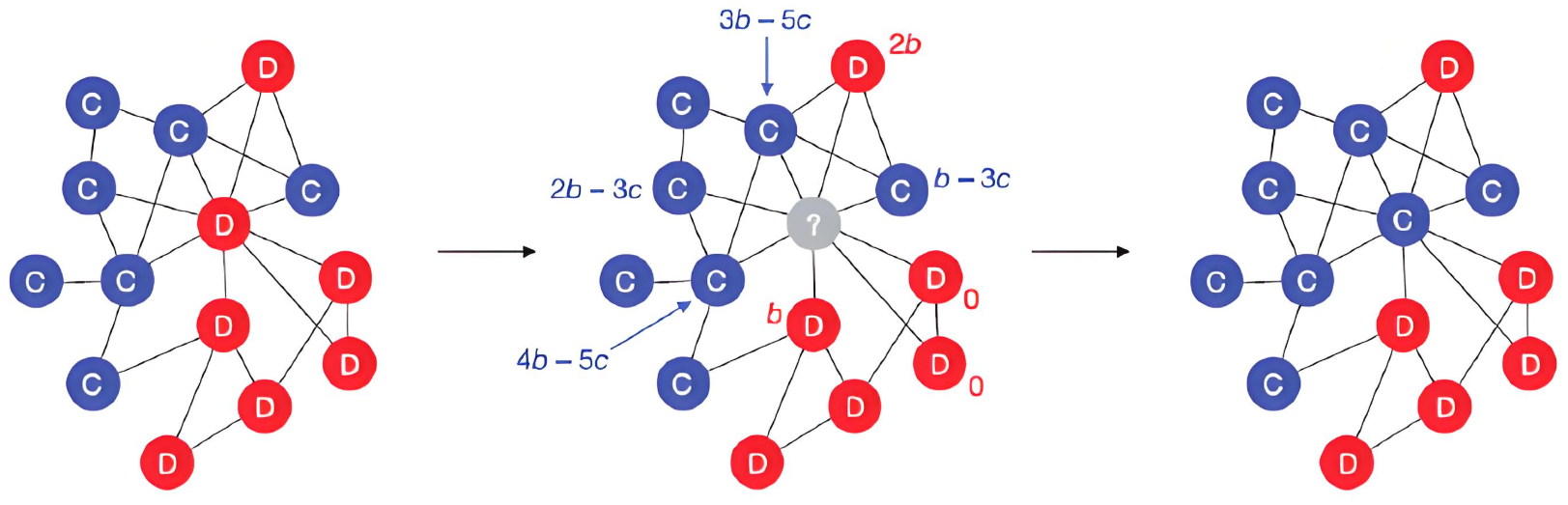
一、引言
在合作博弈论中,如何公平地在多个参与者之间分配联合收益是核心问题之一。Shapley值为我们提供了一种公平分配机制。然而,在现实网络中,参与者之间的合作并非总是自由进行,而是受到网络结构的限制。此时,经典的Shapley值已无法直接适用。迈尔森值(Myerson Value)的提出,正是为了解决网络限制下的合作分配问题。
这里将系统介绍迈尔森值的定义、理论背景,并通过案例展示其在网络合作博弈中的应用。最后我们还将对比Shapley值与Myerson值,理解它们的异同。
二、背景知识:合作博弈与Shapley值
2.1 合作博弈(Cooperative Game)
一个合作博弈可以用集合函数表示为:
其中 \(N\) 是玩家集合,\(v(S)\) 表示子集 \(S \subseteq N\) 中玩家可以联合获得的总价值。
2.2 Shapley值
Shapley值是解决“每个玩家应获得多少收益”的公平分配机制。其定义如下:
- 每个玩家 \(i\) 的 边际贡献 被加权平均;
- 满足效率、公平性、对称性等性质;
- 假设所有联盟均可实现。
三、迈尔森值的提出:引入图结构限制
3.1 图限制合作博弈
在很多现实中,参与者并非可以任意合作,而是通过网络连接进行互动。例如:
- 社交网络中的信息传播;
- 企业之间基于合作协议的联盟;
- 基因网络中的共调控机制。
此时,可行的联盟仅为图中连通子图。
3.2 Myerson博弈模型
Myerson(1977)提出的 图限制合作博弈(Graph-restricted Cooperative Game),是对经典合作博弈的一个扩展,用以刻画联盟结构受到图连接限制的情形。其形式可由如下四元组表示:
其中:
- $ N $:玩家集合,表示参与博弈的所有个体;
- $ v $:特征函数,定义为 $ v: 2^N \rightarrow \mathbb{R} $,赋予任意联盟 $ S \subseteq N $ 一个价值 $ v(S)$,满足 $ v(\emptyset) = 0 $;
- $ G = (N, E)$:一个无向图,其中边集 $ E \subseteq { {i, j} \mid i, j \in N, i \ne j } $,表示哪些玩家之间存在直接的合作连接;
- $ \mu $:Myerson值,即在网络结构 $ G $ 限制下,基于调整后的图限制特征函数 $ v^G $ 所计算得到的 Shapley 值,表示每位玩家应得的公平分配。
该模型充分考虑了联盟可达性限制与分配公平性之间的平衡,为解决社会网络、通信系统、供应链协同等领域中的合作博弈问题提供了理论基础。
3.3 Myerson值定义
核心思想:
将原博弈 \(v\) 根据图 \(G\) 进行“限制”,得到一个新的合作博弈 \(v^G\),然后对 \(v^G\) 应用Shapley值,即为迈尔森值。
定义如下:
Step 1:构造限制函数 \(v^G\)
对于任意联盟 \(S \subseteq N\),若该子图在 \(G\) 上被分为若干连通分量 \(C_1, C_2, ..., C_k\),则:
即:联盟 \(S\) 的价值为其连通部分的独立价值之和。
Step 2:对 \(v^G\) 应用Shapley值
即为玩家 \(i\) 的Myerson值。
四、案例分析:三节点图结构
4.1 问题设定
考虑如下合作博弈 \(v\) 和图结构 \(G\):
- 玩家集合:\(N = \{1, 2, 3\}\);
- 博弈函数 \(v(S)\) 定义如下:
| 联盟 \(S\) | $$v(S)$$ |
|---|---|
| \(\{1\}\) | 0 |
| \(\{2\}\) | 0 |
| \(\{3\}\) | 0 |
| \(\{1,2\}\) | 100 |
| \(\{2,3\}\) | 100 |
| \(\{1,3\}\) | 0 |
| \(\{1,2,3\}\) | 120 |
- 图结构 \(G\):
1 —— 2 —— 3
图是一个路径:1 与 2 相连,2 与 3 相连,1 与 3 不直接相连。
4.2 构造限制博弈 \(v^G\)
根据连通性规则:
| 联盟 \(S\) | 连通子集 | \(v^G(S)\) |
|---|---|---|
| \(\{1,2\}\) | \(\{1,2\}\) | 100 |
| \(\{2,3\}\) | \(\{2,3\}\) | 100 |
| \(\{1,3\}\) | \(\{1\}, \{3\}\) | 0 + 0 = 0 |
| \(\{1,2,3\}\) | \(\{1,2,3\}\) | 120 |
于是我们得到限制博弈 \(v^G\),再基于此计算Shapley值即可得到迈尔森值。
4.3 迈尔森值计算(Python实现)
from itertools import permutations, combinations
def marginal_contribution(vg, player, perm):
contrib = 0
S = set()
for p in perm:
if p == player:
key = frozenset(S | {p})
contrib = vg.get(key, 0) - vg.get(frozenset(S), 0)
break
S.add(p)
return contrib
def shapley_value(players, vg):
n = len(players)
factorial = lambda x: 1 if x == 0 else x * factorial(x - 1)
phi = dict.fromkeys(players, 0.0)
perms = list(permutations(players))
for p in perms:
for i in players:
contrib = marginal_contribution(vg, i, p)
phi[i] += contrib
for i in players:
phi[i] /= factorial(n)
return phi
# 限制博弈 v^G
vg = {
frozenset(): 0,
frozenset({1}): 0,
frozenset({2}): 0,
frozenset({3}): 0,
frozenset({1, 2}): 100,
frozenset({2, 3}): 100,
frozenset({1, 3}): 0,
frozenset({1, 2, 3}): 120,
}
players = [1, 2, 3]
myerson_val = shapley_value(players, vg)
print("迈尔森值:", myerson_val)
五、Myerson值 vs Shapley值
Shapley值是合作博弈论中最经典的分配方法,旨在根据每位玩家对联盟总价值的边际贡献,进行公平收益分配。然而,在真实的网络中,合作常常受到结构限制,玩家之间不能任意组合成联盟。这种场景下,Myerson(1977)提出了图限制合作博弈(Graph-restricted Cooperative Game),引入了“网络约束”的思想,提出了Myerson值,作为Shapley值在图结构下的扩展。
5.1 无向网络
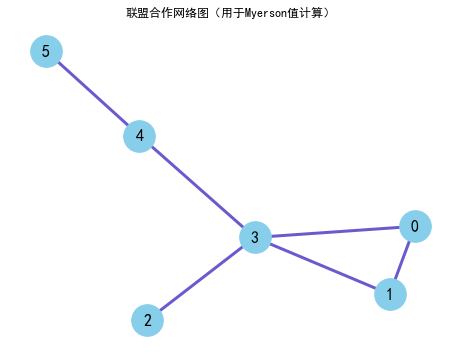
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib
# 支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False
# 创建图结构
G = nx.Graph()
G.add_edges_from([
(0, 1), (0, 3), (1, 3), (2, 3),
(3, 4), (4, 5)
])
# 获取布局
pos = nx.spring_layout(G, seed=42)
# 绘图
plt.figure(figsize=(8, 6))
nx.draw_networkx(
G, pos,
with_labels=True,
node_color='skyblue',
edge_color='#6A5ACD', # 蓝紫色边
width=3.0, # 加粗线条
node_size=1000,
font_size=16
)
plt.title("联盟合作网络图(用于Myerson值计算)")
plt.axis('off')
plt.show()
5.2 Sharpley值计算
设定每个联盟的价值函数为:
即联盟中成员越多,整体合作价值越大。
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib
import itertools
import numpy as np
from collections import defaultdict
# 支持中文显示
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False
# === 1. 创建联盟网络 ===
G = nx.Graph()
G.add_edges_from([
(0, 1), (0, 3), (1, 3), (2, 3),
(3, 4), (4, 5)
])
pos = nx.spring_layout(G, seed=42)
plt.figure(figsize=(8, 6))
nx.draw_networkx(G, pos, with_labels=True,
node_color='skyblue', edge_color='gray',
node_size=1000, font_size=16)
plt.title("联盟合作网络图(用于Myerson值计算)")
plt.axis('off')
plt.show()
# === 2. 定义合作价值函数 ===
def v(S):
return len(S) ** 2 # 任意子集的价值为其大小的平方
# === 3. Shapley 值计算函数 ===
def shapley_value(N, v_func):
n = len(N)
shapley = defaultdict(float)
for pi in itertools.permutations(N):
S = set()
for i in pi:
S_prev = S.copy()
S.add(i)
delta = v_func(S) - v_func(S_prev)
shapley[i] += delta
for i in N:
shapley[i] /= np.math.factorial(n)
return dict(sorted(shapley.items()))
# === 4. 计算 Shapley 值 ===
N = list(G.nodes())
shapley_vals = shapley_value(N, v)
# === 5. 输出结果 ===
print("Shapley 值结果(每个节点的贡献值):")
for k, val in shapley_vals.items():
print(f"节点 {k}: {val:.2f}")
5.3 Myerson值的计算(考虑网络限制)
import networkx as nx
import matplotlib.pyplot as plt
import matplotlib
import itertools
import numpy as np
from collections import defaultdict
# === 设置 matplotlib 显示中文 ===
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False
# === 1. 创建联盟网络图 ===
G = nx.Graph()
G.add_edges_from([
(0, 1), (0, 3), (1, 3), (2, 3),
(3, 4), (4, 5)
])
pos = nx.spring_layout(G, seed=42)
plt.figure(figsize=(8, 6))
nx.draw_networkx(G, pos, with_labels=True,
node_color='skyblue', edge_color='gray',
node_size=1000, font_size=16)
plt.title("联盟合作网络图(用于Shapley值和Myerson值计算)")
plt.axis('off')
plt.show()
# === 2. 定义联盟价值函数 ===
def v(S):
return len(S) ** 2 # 基础价值函数:节点数的平方
# === 3. Shapley值计算函数 ===
def shapley_value(N, v_func):
n = len(N)
shapley = defaultdict(float)
for pi in itertools.permutations(N):
S = set()
for i in pi:
delta = v_func(S | {i}) - v_func(S)
shapley[i] += delta
S.add(i)
for i in N:
shapley[i] /= np.math.factorial(n)
return dict(sorted(shapley.items()))
# === 4. Myerson值计算支持函数 ===
def v_G(G, coalition):
subgraph = G.subgraph(coalition)
comps = nx.connected_components(subgraph)
return sum(v(comp) for comp in comps)
def myerson_value(G, v_func):
N = list(G.nodes())
n = len(N)
values = defaultdict(float)
for pi in itertools.permutations(N):
S = set()
for i in pi:
delta = v_G(G, S | {i}) - v_G(G, S)
values[i] += delta
S.add(i)
for i in N:
values[i] /= np.math.factorial(n)
return dict(sorted(values.items()))
# === 5. 计算并输出 Shapley 值 ===
N = list(G.nodes())
shapley_vals = shapley_value(N, v)
print("\n✅ Shapley 值(忽略网络结构):")
for i, val in shapley_vals.items():
print(f"节点 {i}: {val:.2f}")
# === 6. 计算并输出 Myerson 值 ===
myerson_vals = myerson_value(G, v)
print("\n✅ Myerson 值(考虑网络限制):")
for i, val in myerson_vals.items():
print(f"节点 {i}: {val:.2f}")
5.4 Shapley值 与 Myerson值的比较
| 特征维度 | Shapley值 | Myerson值(Myerson Value) |
|---|---|---|
| 联盟假设 | 所有 \(2^N\) 个子集均可自由组成联盟(不考虑网络限制) | 仅允许联盟中节点构成图 \(G\) 的连通子图(必须有通路) |
| 合作范围 | 所有节点集合,无限制的完全合作环境 | 局限于网络中的可连通节点子集 |
| 核心思想 | 每个参与者在所有可能排列中的边际贡献的期望值 | 基于图约束的价值函数 \(v^G\),再计算其Shapley值 |
| 计算方式 | $$\phi_i = \sum_{\pi \in \Pi} \left[v(S_i \cup {i}) - v(S_i)\right] / n!$$ | 同上公式,但使用变换后的图限制函数 \(v^G(S)\) |
| 价值函数 | \(v(S)\),对任意节点集合 \(S\) 定义的原始函数 | \(v^G(S)\),将 \(S\) 拆分为图中连通分量再分别求和 |
| 合作模型 | 假设所有成员可完全沟通与协调 | 限于图结构中可连通的成员才能合作 |
| 适用场景 | 抽象博弈论、拍卖、收益分配等无通信限制情形 | 通信网络、供应链、社交网络、地理受限合作等 |
| 公平性含义 | 对所有玩家公平地分摊其平均边际贡献 | 对所有“能合作”的连接个体公平地分配局部价值 |
| 对结构敏感性 | 不依赖图结构;每个节点的贡献不因位置变化 | 强烈依赖图结构;桥梁或枢纽节点更关键 |
| 示例中的值 | 节点 0–5 均为 6.00,说明完全公平对称 | 节点 3 值最大(10.50),因其是关键连接桥梁 |
| 是否考虑信息/传播限制 | 否(全知全能设定) | 是(信息或合作受网络传递限制) |
📌 计算结果对比如下:
| 节点 | Shapley值 | Myerson值 |
|---|---|---|
| 节点 0 | 6.00 | 4.83 |
| 节点 1 | 6.00 | 4.83 |
| 节点 2 | 6.00 | 4.50 |
| 节点 3 | 6.00 | 10.50 |
| 节点 4 | 6.00 | 7.17 |
| 节点 5 | 6.00 | 4.17 |
🔍 分析解读:
- Shapley值体现了在“没有网络限制”的纯理论场景中,节点地位是对称的,因此每个节点分得的价值完全相同。
- Myerson值更贴近现实网络中的合作情形,桥梁节点(如节点3)因连接多个团体,贡献更大,获得的价值更多。
- 节点 5 的 Myerson值最小,因它仅通过节点 4 与他人连接,处于边缘位置,合作能力受限。
六、结语
迈尔森值作为Shapley值的一个重要扩展,为存在网络结构限制的合作博弈提供了公平且合理的解决方案。在传统的合作博弈中,任意一组参与者都可以组成联盟,但在现实生活中,如社交网络、通信系统、供应链联盟以及科研合作网络等,玩家之间是否能够合作往往受到结构性条件的限制,只有在图结构中连通的个体才具备联合行动的可能性。
迈尔森值正是针对这种“受限合作”情形提出的一种收益分配规则,它不仅继承了Shapley值关于对称性、线性性、边际贡献等公平原则,还引入图结构中“可达性”的概念,从而在分配收益时更加符合实际。它通过将图中每个联盟的贡献重新定义为其在连通子图中的Shapley值加总,构建出适应网络的分配逻辑。
随着社会网络分析、平台经济、区块链治理等领域的迅猛发展,迈尔森值的理论与应用价值日益显著。未来,如何在大规模图结构中高效计算迈尔森值、如何推广至动态或不完全信息网络中,将成为网络博弈与算法机制设计中的重要研究方向。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号