网络博弈——复杂网络建模与特征分析

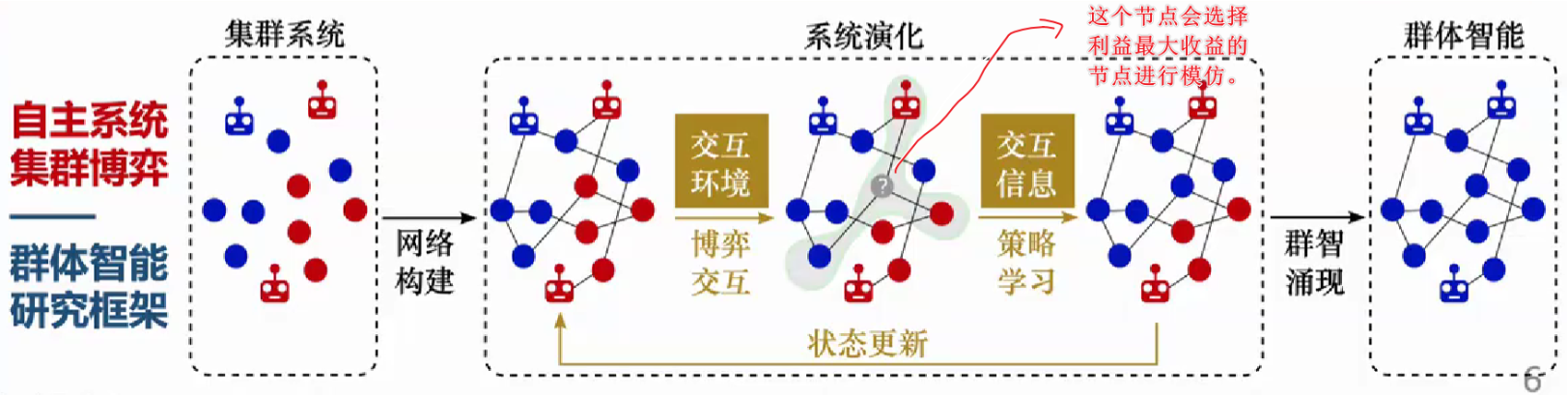
在传统博弈论中，参与者通常被假设为在完全连接的环境中进行策略互动，即每个个体的决策均可能直接影响所有其他个体。然而，现实世界中的博弈行为往往受限于特定的社会关系、空间位置或信息路径，这些因素构成了一个复杂的网络结构。网络不仅定义了个体之间的互动范围，也深刻影响了策略传播、协同行为的稳定性以及均衡状态的演化过程。因此，将博弈论与网络科学相结合，形成“网络博弈”（Network Game）的研究框架，成为刻画复杂系统中局部互动与整体行为的重要工具。网络博弈不仅揭示了局域连接对全局博弈结果的影响机制，也为解释合作、传播、攻击与控制等多种社会与自然现象提供了理论支持。

引言

在快速发展的信息社会中，个体之间的行为不再是孤立进行的，而是通过各种显性或隐性的网络结构相互作用。无论是人与人之间的社交关系、企业之间的市场竞争，还是网络中的信息传播过程，都表现出强烈的“网络性”与“博弈性”。传统博弈论主要研究在理性前提下多个参与者之间的策略互动，但其大多假设所有个体之间可以自由互动。然而，现实中的互动往往受到结构限制，网络的存在使得个体仅能与有限的邻居发生策略关系。这便引出了一个关键的研究框架——网络博弈（Network Games）。

0.1 什么是网络博弈？

网络博弈是博弈论与网络科学的交叉领域，其核心思想是在给定网络结构下研究个体之间的博弈互动。在这一框架中，个体（节点）之间的策略选择与其网络邻居之间的关系密切相关。每个节点的收益不仅依赖于自己的选择，还受其连接节点的策略影响。网络的拓扑结构，例如度分布、聚类系数或中心性，不仅决定了信息与影响力的传播路径，也决定了博弈的演化结果。网络博弈的理论框架为刻画局部互动、有限理性和复杂行为提供了更贴近现实的工具。

0.2 网络博弈的现实背景与重要性

网络博弈的研究之所以重要，是因为现实生活中充满了结构性互动场景：

社交网络：在Facebook、微信或Twitter等社交平台中，用户的行为（如转发、点赞、抵制）常常受到邻居行为的影响。例如，一个人是否传播虚假信息，很大程度上取决于他社交圈中其他人的行为模式。
互联网平台竞争：平台如淘宝、京东、美团等，在价格制定、用户补贴和服务设计等方面都存在策略互动，而这种互动通常发生在一个包含市场参与者与用户的网络中，影响路径具有局域性。
信息扩散与舆情演化：热点事件、公共政策或危机事件的舆论传播，往往表现出节点之间相互模仿、抵抗或加强的行为链。这种过程中，网络结构决定了信息是否形成“瀑布效应”，并进一步影响公共决策。

网络博弈不仅能够帮助我们理解这些现象背后的微观动因，还能为政策设计、平台机制优化和群体行为预测提供理论支持。

0.3 网络博弈的发展历程

网络博弈作为博弈论与网络科学融合的产物，其发展可以追溯到20世纪末复杂网络理论的兴起阶段。在此之前，传统博弈模型主要以完全信息和完全连接的参与者群体为分析前提，无法有效刻画现实社会中局域互动和结构异质性的复杂性。
随着1998年Barabási和Albert提出无标度网络模型，以及Watts和Strogatz提出小世界网络模型，学者们逐渐认识到现实中的社会、技术与生物网络呈现出高度聚集性和幂律分布特征。这些发现促使研究者重新思考博弈过程在网络中的运作机制。
2000年前后，Nowak等人将**演化博弈论（Evolutionary Game Theory）**引入网络环境，开启了复杂网络中的演化合作研究。随后，Jackson和Wolinsky（1996）开创了网络形成博弈（network formation games）框架，研究网络本身作为博弈结果的形成过程。近年来，随着多智能体系统、社交媒体平台和区块链技术的发展，网络博弈已扩展至多种应用领域，包括：病毒传播建模、推荐系统机制、市场机制设计以及信息安全博弈等，成为理论研究与实践应用并重的重要方向。

一、博弈论基础与网络结构回顾

在进入“网络博弈”的世界之前，我们有必要先回顾博弈论和网络科学这两个关键基础。它们就像搭建复杂系统的两根支柱——一个强调个体之间的战略互动，另一个刻画互动发生的结构场景。网络博弈的核心正是两者的交叉与融合。

1.1 博弈论的基本要素

我们从最基础的定义出发：

博弈（Game）是一种描述多个理性参与者在特定规则下进行战略互动的模型。

博弈由如下几个要素构成：

参与者（Players）：通常用集合 $N = {1,2,\ldots,n}$ 表示。
策略集（Strategies）：第 $i$ 个玩家的策略集为 $S_i$，完整策略组合为 $S = S_1 \times S_2 \times \cdots \times S_n$。
支付函数（Payoff Functions）：每个玩家都有一个支付函数 $u_i : S \rightarrow \mathbb{R}$，表示在所有人采取策略 $s \in S$ 时，第 $i$ 个玩家获得的收益。

一个标准博弈可以形式化为：

\[G = (N, \{S_i\}_{i \in N}, \{u_i\}_{i \in N}) \]

🎯 纳什均衡（Nash Equilibrium）

一组策略组合 $s^* = (s_1^* , s_2^* , \ldots, s_n^*)$ 是纳什均衡，如果对每个玩家 $i$ 有：

\[u_i(s_i^*, s_{-i}^*) \ge u_i(s_i, s_{-i}^*), \quad \forall s_i \in S_i \]

也就是说，在其他人策略不变的情况下，没有人有动机单独改变自己的策略。

1.2 网络结构基础回顾

📎 为什么引入网络？

现实生活中的互动往往不是完全对称的。一个人只与周围若干人互动，比如：

社交网络中的好友圈；
企业供应链中的上下游关系；
网络攻击与防御中的节点拓扑。

因此，我们需要使用图论来刻画这些局部互动关系。

📐 网络（图）的基本概念

一个网络形式上是一个图 $G = (V, E)$，其中：

$V$ 是节点集合（玩家）；
$E \subseteq V \times V$ 是边集合，表示相互作用关系。

可能的扩展包括：

有向图：边 $(i, j)$ 表示信息只从 $i$ 影响 $j$；
加权图：边权重 $w_{ij}$ 表示关系强度；
动态图：网络结构随时间变化 $G(t)$。

🔍 常用网络指标

指标名称	数学定义或意义
度数（Degree）	节点连接边的数量，$d_i = \text{deg}(i)$
平均路径长度	任意两点最短路径的平均值
聚类系数	一个节点的邻居间彼此连接的概率
中心性	如介数中心性、特征向量中心性，衡量节点重要性

🧠 现实网络的典型类型

类型	特征
随机图	边随机连接，节点度数近似服从泊松分布
小世界网络	高聚类 + 小平均路径，例如Watts-Strogatz模型
无标度网络	节点度数遵循幂律分布，存在少数超级连接点

1.3 网络博弈的基本思路

结合博弈论与网络结构，就形成了网络博弈（Network Game）：

网络博弈是博弈的参与者嵌入到网络图结构中，博弈的影响仅限于其邻居节点（局部交互）。

形式化定义如下：

网络 $G = (V,E)$，每个节点 $i \in V$ 是一个玩家；
每个玩家 $i$ 与其邻居 $N_i$ 进行局部博弈；
玩家选择策略 $s_i$；
支付函数 $u_i(s_i, {s_j : j \in N_i})$ 仅依赖于其邻居。

这种模型被称为局部相互作用博弈（Local Interaction Games），也常用于**演化博弈论（Evolutionary Games）**框架中。

1.4 局部 vs 全局博弈的对比

维度	全局博弈（Classical）	网络博弈（Networked）
玩家关系	所有玩家直接互动	仅与邻居互动（通过网络结构）
支付函数	$u_i(s_1, \ldots, s_n)$	$u_i(s_i, {s_j : j \in N_i})$
信息结构	全局可知	局部可知
策略影响	全局耦合	局部耦合
应用领域	博弈论传统模型，如拍卖、投票等	网络扩散、社交协作、信息防御等

1.5 示例：网络中的囚徒困境

节点A —— 节点B —— 节点C

每个节点与其邻居进行囚徒困境博弈；
A 与 B 对弈，B 同时与 A 和 C 对弈；
每个节点总收益是所有邻居博弈的总和。

若 B 合作，而 A 与 C 均背叛，B 将处于不利位置；但如果网络结构促进合作传播（例如多数邻居合作），那么合作可能成为稳定策略。这就是网络结构对博弈结果的巨大影响。

二、网络博弈模型分类与定义

网络博弈研究的是在网络结构中个体之间的策略互动与博弈行为。相比于传统博弈模型，网络博弈引入了显式的图结构，使得参与者的交互局限于其邻居节点。本章系统梳理网络博弈的定义与分类方式，并给出常见模型示例。

2.1 网络博弈的基本定义（Formal Definition）

令图 $G = (V, E)$ 表示一个网络，其中 $V = \{1, 2, \dots, n\}$ 是节点集合，每个节点表示一个博弈参与者，$E$ 为边集合，表示节点之间的连接关系。每个玩家 $i \in V$ 有一个策略集合 $S_i$，其收益函数定义为：

\[u_i(s_i, s_{N(i)}) : S_i \times \prod_{j \in N(i)} S_j \to \mathbb{R} \]

其中 $N(i)$ 表示节点 $i$ 的邻居集合，$s_{N(i)}$ 为其邻居的策略组合。

网络博弈（Network Game）即为四元组：

\[G = (V, E, \{S_i\}_{i \in V}, \{u_i\}_{i \in V}) \]

其核心特征在于收益依赖于局部结构而非全局信息。

2.2 分类方式一：博弈类型划分

（1）静态 vs 动态网络博弈

静态网络博弈：网络结构固定，研究单次或多次在既定图上的策略演化。
动态网络博弈：网络结构随时间演化，节点或边可变，如社交网络形成过程中的连接断裂或新建。

（2）完全信息 vs 不完全信息

完全信息：玩家了解博弈规则、网络结构、邻居策略等完整信息。
不完全信息：玩家仅知局部网络，无法观察邻居全部行为，博弈中存在信息不对称。

2.3 分类方式二：策略交互方式

本地相互作用博弈（Local Interaction Games）

玩家仅与邻居博弈；
收益函数依赖于邻居策略；
适用于建模社交行为、病毒传播等。

网络合作博弈（Networked Cooperative Games）

允许玩家结成联盟、分享资源；
使用图论工具刻画连接强度、分配规则；
常用于联合投资、任务协作等情境。

2.4 分类方式三：信息结构

同质网络 vs 异质网络

同质网络：节点属性一致，连接规则对称。
异质网络：节点具有不同特征（如影响力、资源量），连接强弱不一。

有向图 vs 无向图

无向图：节点间互动是双向对等的。
有向图：存在单向影响，如信息流、关注关系等。

2.5 常见形式化模型举例

（1）图上囚徒困境模型

节点策略：合作（C）或背叛（D）；
与邻居一对一博弈，累计总收益；
博弈结果取决于局部合作密度。

（2）网络公共品博弈模型

每个节点决定贡献程度 $x_i$；
邻居的贡献总和影响公共资源；
收益函数形如：$u_i = a \cdot \sum_{j \in N(i)} x_j - c \cdot x_i$。

（3）网络协作与分配模型

联盟形成与资源分配；
Shapley值、核解、边权博弈等；
研究个体如何根据连接结构分配合作收益。

三、本地相互作用博弈详解

本章深入分析一种常见的网络博弈类型——本地相互作用博弈（Local Interaction Game），该模型强调每个参与者只与其邻居进行局部策略互动，并基于局部信息更新行为。

3.1 模型框架与形式化定义

在图 $G=(V,E)$ 中，设每个节点 $i$ 仅与邻居 $N(i)$ 互动，其收益函数可形式化为：

\[u_i(s_i, s_{N(i)}) = \sum_{j \in N(i)} \phi(s_i, s_j) \]

其中 $\phi$ 是局部博弈函数，表示 $i$ 与 $j$ 的博弈收益。

此模型强调两个特征：

玩家仅与邻居博弈；
网络结构决定互动范围。

3.2 典型模型：图上囚徒困境（Prisoner’s Dilemma on Graph）

数学表示

设合作收益 $R$，背叛收益 $T$，惩罚收益 $P$，受害收益 $S$，满足 $T > R > P > S$。

每个节点选择 $C$ 或 $D$，对其邻居分别执行 PD 博弈，总收益为所有邻居对局的加总。

均衡分析

若所有邻居均合作，则合作为局部最优；
若邻居中背叛者比例较高，合作将被侵蚀；
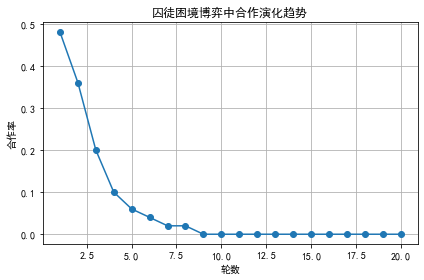
局部演化可能导致系统性退化（“合作灭绝”）或局部合作簇的形成。

稳定状态图示演化

通过模拟演化，可观察：

合作在边缘节点更易存活；
网络结构（如聚类）有助于合作群体维持；
小世界网络提升全局合作可能性。

3.3 潜在博弈与最优性

潜在函数定义

若存在函数 $\Phi(s)$ 满足：

\[u_i(s_i', s_{-i}) - u_i(s_i, s_{-i}) = \Phi(s_i', s_{-i}) - \Phi(s_i, s_{-i}) \]

则称该网络博弈为潜在博弈（Potential Game）。

动态演化与稳定性

潜在函数单调上升意味着系统趋于稳定；
局部最优即纳什均衡；
模拟退火或扰动机制可跳出局部最优陷阱。

3.4 本地博弈均衡性质分析

局部纳什均衡（Local Nash Equilibrium）

一个策略组合 $s^*$ 满足：

\[\forall i, \quad s_i^* = \arg\max_{s_i} u_i(s_i, s_{N(i)}) \]

即每个节点相对于邻居不可单边提升收益。

最佳响应动力学（Best Response Dynamics）

一种策略更新方式：

每轮选择一个节点；
其观察邻居策略，选择使自身收益最大的响应；
系统最终收敛于局部纳什均衡。

3.5 示例：模拟一个本地博弈过程

以下为图上囚徒困境的简化模拟框架：

import matplotlib
import matplotlib.pyplot as plt
import networkx as nx
import random
import numpy as np

# 设置中文字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

# 初始化图
def initialize_network(n):
    G = nx.erdos_renyi_graph(n, 0.1)
    strategies = {node: random.choice(['C', 'D']) for node in G.nodes}
    return G, strategies

# 计算收益
def calculate_payoff(G, strategies, node):
    R, T, S, P = 3, 5, 0, 1  # 囚徒困境参数
    payoff = 0
    for neighbor in G.neighbors(node):
        if strategies[node] == 'C' and strategies[neighbor] == 'C':
            payoff += R
        elif strategies[node] == 'C' and strategies[neighbor] == 'D':
            payoff += S
        elif strategies[node] == 'D' and strategies[neighbor] == 'C':
            payoff += T
        else:
            payoff += P
    return payoff

# 更新策略
def update_strategies(G, strategies):
    new_strategies = strategies.copy()
    for node in G.nodes:
        neighbors = list(G.neighbors(node))
        if not neighbors:
            continue
        neighbor = random.choice(neighbors)
        payoff_self = calculate_payoff(G, strategies, node)
        payoff_neighbor = calculate_payoff(G, strategies, neighbor)
        if payoff_neighbor > payoff_self:
            prob = (payoff_neighbor - payoff_self) / (len(neighbors) * 5)
            if random.random() < prob:
                new_strategies[node] = strategies[neighbor]
    return new_strategies

# 绘图函数
def draw_network(G, strategies, t):
    color_map = ['blue' if strategies[node] == 'C' else 'red' for node in G.nodes]
    pos = nx.spring_layout(G, seed=42)
    fig, ax = plt.subplots(figsize=(6, 4))
    nx.draw_networkx_nodes(G, pos, node_color=color_map, node_size=50, ax=ax)
    nx.draw_networkx_edges(G, pos, edge_color='gray', ax=ax)
    ax.set_title(f"第 {t} 轮策略分布（蓝=C，红=D）")
    ax.axis('off')
    plt.tight_layout()
    plt.show()

# 主程序
n = 50
rounds = 20
G, strategies = initialize_network(n)

coop_rates = []

for t in range(1, rounds + 1):
    draw_network(G, strategies, t)
    coop_rate = list(strategies.values()).count('C') / n
    coop_rates.append(coop_rate)
    strategies = update_strategies(G, strategies)

# 绘制合作率变化图
plt.figure()
plt.plot(range(1, rounds + 1), coop_rates, marker='o')
plt.xlabel("轮数")
plt.ylabel("合作率")
plt.title("囚徒困境博弈中合作演化趋势")
plt.grid(True)
plt.tight_layout()
plt.show()

第1轮	第10轮	演化趋势

四、网络合作博弈（Networked Cooperative Games）

拓展分析在网络结构下的合作博弈（Cooperative Games on Networks），即多个个体在存在局部连接限制的图结构中，围绕集体收益如何划分、联盟如何形成的问题展开合作行为。不同于本地相互作用博弈中的非合作决策，这里聚焦联盟形成与收益分配机制，强调集体理性与局部约束并存的制度设计。

4.1 模型框架与基本定义

设网络结构为图 $G = (V, E)$，其中 $V$ 表示玩家集合，$E$ 为玩家间的连接关系。每个玩家 $i \in V$ 通过与其邻居协作形成子联盟。整个博弈由一个合作函数 $v: 2^V \to \mathbb{R}$ 描述，即任何玩家子集 $S \subseteq V$ 所能实现的最大收益 $v(S)$。

网络合作博弈的关键特征包括：

网络限制：只有在图上连通的玩家集合 $S$ 才能形成有效联盟；
收益分配问题：需设计合理机制分配 $v(S)$ 到每个 $i \in S$；
稳定性与理性：考察是否存在稳定、合理的收益划分，使任何子集玩家无动力脱离现有联盟。

我们称该博弈为网络限制合作博弈（Cooperative Game with Communication Graph Constraints）。

4.2 联盟形成与通信结构

连通联盟集

定义可行联盟集合为：

\[\mathcal{F}(G) = \{ S \subseteq V : G[S] \text{是连通图} \} \]

即只有当子图 $G[S]$ 连通时，$S$ 才能构成联盟。

通信博弈模型（Myerson Game）

Myerson（1977）提出了在网络结构下考虑合作的模型：引入一个修改的特征函数 $v_G(S)$，仅对连通联盟赋值，其余置为零：

\[v_G(S) = \begin{cases} v(S), & \text{if } S \in \mathcal{F}(G) \\ 0, & \text{otherwise} \end{cases} \]

此修改后的博弈 $v_G$ 被称为Myerson博弈，代表了通信限制对合作结果的直接影响。

4.3 收益分配与Myerson值

在网络结构下，经典的Shapley值难以直接应用，因为不是所有联盟都可形成。为此，Myerson定义了一个Myerson值（Myerson Value），作为一种适应通信结构的收益分配方案。

Myerson值定义

对每个玩家 $i \in V$，其Myerson值定义如下：

\[\phi_i^G(v) = \sum_{S \subseteq V \setminus \{i\}} \frac{|S|!(|V|-|S|-1)!}{|V|!} \cdot \left[v_G(S \cup \{i\}) - v_G(S)\right] \]

其含义为：对所有可能的玩家排列中，$i$ 对形成联盟边界的边际贡献的期望。

Myerson值性质

效率性：$\sum_{i \in V} \phi_i^G(v) = v_G(V)$；
对称性：若两个玩家在图中处境等价（同构），则其Myerson值相等；
边界一致性：若两个玩家之间的连接被移除，其合作价值减少体现在Myerson值中。

这种方法既考虑了合作收益，又体现了网络限制，是一种局部理性下的全局最优分配机制。

4.4 稳定性分析与核心（Core）约束

在合作博弈中，核心（Core）是指一组收益分配，使得没有任何联盟 $S$ 会因当前分配而有动力单独合作。

网络核心定义

考虑网络限制后的核心定义如下：

\[\text{Core}(v_G) = \left\{ x \in \mathbb{R}^{|V|} \;\middle|\; \sum_{i \in V} x_i = v_G(V), \; \sum_{i \in S} x_i \ge v_G(S),\; \forall S \in \mathcal{F}(G) \right\} \]

若核心非空，则存在一种稳定分配，使所有连通子联盟都无动力脱离。

稳定性讨论

网络结构稀疏时，可能出现大量稳定分配；
若某些关键节点被断开，整个博弈可碎裂为多个子博弈；
若网络为树，则Shapley值与Myerson值一致，且核心总非空。

4.5 示例：3人网络合作博弈演化

考虑图 $G$ 为简单链状结构 $1 - 2 - 3$，特征函数定义为：

$v(\{1\}) = v(\{2\}) = v(\{3\}) = 0$；
$v(\{1,2\}) = 10,\; v(\{2,3\}) = 12,\; v(\{1,2,3\}) = 18$

则连通联盟为 $\mathcal{F}(G) = \{\{1,2\}, \{2,3\}, \{1,2,3\}\}$，Myerson博弈如下：

联盟 $S$	$$v_G(S)$$
$\{1,2\}$	10
$\{2,3\}$	12
$\{1,2,3\}$	18
其他非连通集合	0

我们可通过计算Myerson值（或线性规划法）得到分配方案，例如：

$\phi_1^G = 4$，$\phi_2^G = 9$，$\phi_3^G = 5$

该分配在所有连通子联盟中均满足稳定性约束，因而属于核心。

4.6 Python程序

import matplotlib
import matplotlib.pyplot as plt
import networkx as nx
import random
import numpy as np
from itertools import combinations

# 设置中文字体
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

# 初始化图
def initialize_network(n):
    G = nx.erdos_renyi_graph(n, 0.3, seed=42)
    strategies = {node: random.choice(['C', 'D']) for node in G.nodes}
    return G, strategies

# 计算收益
def calculate_payoff(G, strategies, node):
    R, T, S, P = 3, 5, 0, 1  # 囚徒困境参数
    payoff = 0
    for neighbor in G.neighbors(node):
        if strategies[node] == 'C' and strategies[neighbor] == 'C':
            payoff += R
        elif strategies[node] == 'C' and strategies[neighbor] == 'D':
            payoff += S
        elif strategies[node] == 'D' and strategies[neighbor] == 'C':
            payoff += T
        else:
            payoff += P
    return payoff

# 更新策略
def update_strategies(G, strategies):
    new_strategies = strategies.copy()
    for node in G.nodes:
        neighbors = list(G.neighbors(node))
        if not neighbors:
            continue
        neighbor = random.choice(neighbors)
        payoff_self = calculate_payoff(G, strategies, node)
        payoff_neighbor = calculate_payoff(G, strategies, neighbor)
        if payoff_neighbor > payoff_self:
            prob = (payoff_neighbor - payoff_self) / (len(neighbors) * 5)
            if random.random() < prob:
                new_strategies[node] = strategies[neighbor]
    return new_strategies

# 绘图函数
def draw_network(G, strategies, t):
    color_map = ['blue' if strategies[node] == 'C' else 'red' for node in G.nodes]
    pos = nx.spring_layout(G, seed=42)
    fig, ax = plt.subplots(figsize=(6, 4))
    nx.draw_networkx_nodes(G, pos, node_color=color_map, node_size=300, ax=ax)
    nx.draw_networkx_edges(G, pos, edge_color='gray', ax=ax)
    nx.draw_networkx_labels(G, pos, ax=ax)
    ax.set_title(f"第 {t} 轮策略分布（蓝=C，红=D）")
    ax.axis('off')
    plt.tight_layout()
    plt.show()

# 计算联盟价值
def compute_coalition_values(G, strategies):
    coalition_values = {}
    nodes = list(G.nodes)
    for r in range(1, len(nodes) + 1):
        for coalition in combinations(nodes, r):
            subgraph = G.subgraph(coalition)
            value = 0
            for node in subgraph.nodes:
                value += calculate_payoff(subgraph, strategies, node)
            coalition_values[coalition] = value
    return coalition_values

# 绘制联盟价值柱状图
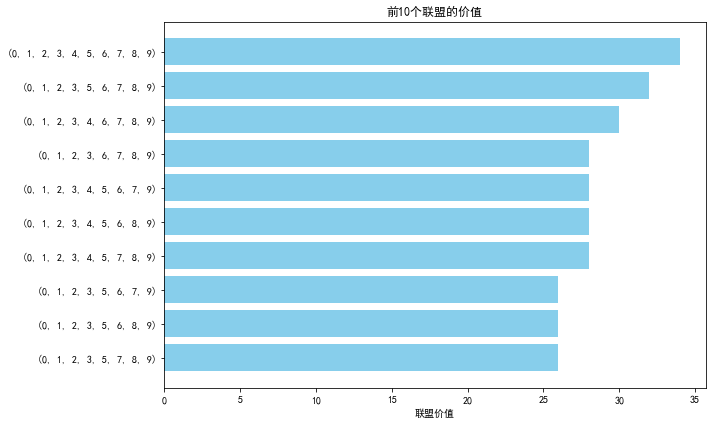
def plot_coalition_values(coalition_values):
    # 选择前10个联盟进行展示
    sorted_coalitions = sorted(coalition_values.items(), key=lambda x: x[1], reverse=True)[:10]
    labels = [str(coalition) for coalition, _ in sorted_coalitions]
    values = [value for _, value in sorted_coalitions]

    plt.figure(figsize=(10, 6))
    plt.barh(labels, values, color='skyblue')
    plt.xlabel("联盟价值")
    plt.title("前10个联盟的价值")
    plt.gca().invert_yaxis()
    plt.tight_layout()
    plt.show()

# 主程序
n = 10
rounds = 10
G, strategies = initialize_network(n)

for t in range(1, rounds + 1):
    draw_network(G, strategies, t)
    strategies = update_strategies(G, strategies)

# 计算并绘制联盟价值
coalition_values = compute_coalition_values(G, strategies)
plot_coalition_values(coalition_values)

第1轮	第6轮	联盟价值

五、算法视角下的网络博弈求解

在网络博弈建模完成后，一个关键问题是如何有效求解博弈均衡、模拟系统演化路径，进而为现实网络设计策略提供可行建议。这儿从算法角度出发，系统整理网络博弈中的主流求解方法，聚焦博弈均衡搜索、强化学习算法、进化模拟方法，并给出代码示例与收敛性分析。

5.1 博弈求解算法概述

网络博弈通常具有大规模、多主体、局部相互作用等特点，传统的解析方法在复杂图结构上往往难以适用，因此需要依赖启发式搜索算法与进化模拟方法来近似寻找最优策略组合。

以下是几种常用方法：

最佳响应动态（Best Response Dynamics）：个体反复调整策略以最大化自己的即时收益，直到达到纳什均衡（若存在）。
模拟退火（Simulated Annealing）：结合概率扰动与全局搜索，在策略空间中寻找近似全局最优解，避免陷入局部最优。
演化算法（Evolutionary Algorithms）：如遗传算法，适用于寻找策略组合的最优适应度分布，尤其适合非凸问题和非线性支付函数。

5.2 图结构下的博弈均衡搜索

网络结构会显著影响均衡的存在性与可计算性。在稀疏图结构中，局部博弈简化全局复杂度；但在密集连接或异构结构中，均衡搜索复杂度激增。

均衡计算复杂度：在一般图上求解纳什均衡是 PPAD-complete 问题，不存在多项式时间算法。
多主体学习算法（Multi-Agent Learning）：各个智能体可通过局部信息与博弈经验自主学习策略，如 Fictitious Play、No-Regret Learning，适合不可知模型。

这些算法的目标不再是严格意义上的精确均衡，而是寻找可接受的策略稳定状态，如演化稳定策略（ESS）或 ε-均衡。

5.3 多智能体博弈与强化学习

强化学习框架为网络博弈中的策略调整与最优行动提供了计算基础。特别是在**图结构+多智能体系统（MAS）**中，强化学习模型可以捕捉个体在有限信息与局部互动下的动态学习过程。

Q-Learning 在网络博弈中的应用：
- 节点以 Q-值更新方式选择策略；
- 邻居行为视作环境动态；
- 奖励函数由收益矩阵给出。
多智能体强化学习（MARL）：
- 所有个体均具备学习能力；
- 存在非平稳性问题；
- 常结合图注意机制或分布式 Q 网络提升学习稳定性。

强化学习框架尤其适用于非静态网络结构下的博弈建模，如节点重连、信息共享与集体协作行为的演化。

5.4 Python示例

import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
import random

# 设置随机种子确保结果可复现
random.seed(42)
np.random.seed(42)

# 参数设置
c = 1         # 公共品供给成本
b = 3         # 公共品总收益
T = 20        # 演化轮数
N = 5         # 节点数
actions = ['G', 'N']  # G: 供给, N: 不供给

# 初始化网络结构
G = nx.Graph()
G.add_edges_from([
    (0, 1), (0, 2),
    (1, 3), (2, 3),
    (3, 4)
])
pos = nx.spring_layout(G, seed=42)

# 初始策略：随机分配 G/N
strategy = {node: random.choice(actions) for node in G.nodes()}

# 演化过程记录
history = []

def calculate_payoff(node, strategy, G):
    """计算当前节点的收益"""
    neighbors = list(G.neighbors(node)) + [node]
    total_payoff = 0
    for neighbor in neighbors:
        if strategy[neighbor] == 'G':
            m = len(list(G.neighbors(neighbor))) + 1
            total_payoff += b / m
    if strategy[node] == 'G':
        total_payoff -= c
    return total_payoff

# 最佳响应动态模拟
for t in range(T):
    new_strategy = strategy.copy()
    for node in G.nodes():
        # 分别尝试 G 与 N 的策略收益
        strategy[node] = 'G'
        payoff_G = calculate_payoff(node, strategy, G)
        strategy[node] = 'N'
        payoff_N = calculate_payoff(node, strategy, G)

        # 选择较优策略
        new_strategy[node] = 'G' if payoff_G > payoff_N else 'N'
    
    strategy = new_strategy.copy()
    history.append(strategy.copy())

    # 打印每轮策略状态
    print(f"轮次 {t + 1} 策略: {strategy}")

# === ✅ 修复关键点：显示策略图，防止 _AxesStack 错误 ===
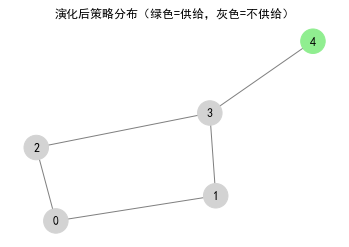
color_map = ['lightgreen' if strategy[node] == 'G' else 'lightgray' for node in G.nodes()]

plt.close('all')  # 清空之前的图像，防止冲突
fig, ax = plt.subplots(figsize=(6, 4))  # 使用 subplot 创建显式坐标轴
nx.draw(G, pos, with_labels=True,
        node_color=color_map,
        node_size=600,
        edge_color='gray',
        ax=ax)  # 显式绑定 ax
ax.set_title("演化后策略分布（绿色=供给，灰色=不供给）")
plt.axis('off')
plt.show()

5.5 算法收敛性与实际应用效果评估

收敛性分析是博弈算法的关键性能指标之一。对演化算法与强化学习而言，常见衡量方法包括：

策略多样性变化趋势；
系统平均收益变化曲线；
达到稳定状态所需轮数（收敛速度）；
多次模拟下策略结果分布的稳定性。

在实际应用中，建议引入如下评估机制：

评估指标	含义
合作率	网络中合作节点占比随时间演化趋势
策略收敛时间	稳定策略分布所需轮数
收益方差	各节点收益差异，衡量不公平性
抗干扰鲁棒性	随机扰动或结构变化后的恢复能力

总体而言，算法的选择需结合网络规模、博弈复杂度与计算资源，多智能体强化学习与进化算法逐渐成为解决网络博弈问题的主流手段，尤其在非线性环境与图结构控制任务中表现优越。

六、应用案例与前沿进展

随着博弈论的发展，网络博弈不仅在理论上不断深化，也在多个现实系统中展现出广泛应用。以下选取三个典型案例，展现网络博弈在不同领域的实用价值与研究潜力。

6.1 案例一：社交媒体中的意见形成博弈

在社交网络中，用户之间的意见影响呈现出典型的博弈特征，特别是人们的言论表达和态度更新常受邻居观点的影响。意见动态模型（Opinion Dynamics Models），如DeGroot模型、Friedkin-Johnsen模型，构建了用户如何在网络中反复调整观点的数学框架。在这些模型中，个体的最终意见状态受邻居平均观点加权影响，并形成纳什均衡或稳态。
舆情演化过程亦呈现出明显的博弈性：用户在转发或评论信息时，不仅权衡个人偏好，还会考虑舆论场中多数立场，从而形成“回音室效应”与“极化现象”。网络结构（如聚集系数、社群分布）与策略更新规则共同影响最终的意见一致性或分歧状态。

6.2 案例二：区块链共识机制中的网络博弈

在区块链系统中，尤其是PoW（Proof-of-Work）机制下，不同矿工节点在挖矿过程中需要博弈性地决定是否诚实遵循协议。区块生成、广播与接收延迟等因素共同作用下，构成了一个动态网络博弈场景。
典型分析模型包括挖矿激励机制博弈与区块选择博弈，其中玩家的策略空间包括是否发布新区块、是否在私链中挖矿（selfish mining）等行为。研究发现，在某些激励参数下，不诚实挖矿者可能获取更高收益，破坏系统公平性，因此必须通过博弈分析设计鲁棒激励机制。

6.3 案例三：流量调度与资源分配博弈

在通信网络与边缘计算环境中，资源（如带宽、计算能力）分布不均，而节点间又存在竞争关系，从而引发网络拥塞博弈（Congestion Games）与资源分配博弈（Resource Allocation Games）。
以边缘计算中的多用户上传任务为例，用户选择最近的服务器、排队或迁移任务等策略受限于带宽延迟、负载平衡等约束条件。通过网络博弈模型，可研究节点间最优分布、演化策略和效率损失（如纳什均衡与社会最优之间的差距），并用于设计自治调度协议。

6.4 网络博弈的挑战与未来趋势

尽管网络博弈理论日趋成熟，但仍面临诸多理论与应用挑战：

非完全理性建模：现实中个体并非严格理性，有限理性模型、经验性行为博弈、强化学习等方法正在引入博弈框架中。
多层网络结构：真实系统往往具有多层次连接结构（如用户社交层+资源分配层），需发展多层网络博弈理论与求解工具。
AI与博弈融合：深度学习、演化算法与博弈模型融合成为前沿热点，用于高维策略空间建模、博弈求解与机制设计。

总结与展望

网络博弈作为传统博弈论与复杂网络理论的交叉融合，为建模现实世界中的互动系统提供了强有力的工具。在社交网络、信息扩散、区块链机制、分布式控制等场景中，网络博弈理论提供了策略行为的深刻洞察。文中从博弈论与网络结构基础出发，系统介绍了网络博弈的模型分类、本地相互作用博弈、演化策略机制等核心内容，并通过多个应用案例展示其理论与实践价值。网络博弈不仅揭示了个体理性行为如何导致集体现象的复杂涌现，还提供了机制设计与行为调控的重要工具。

未来研究可朝如下方向深入：

模型统一与理论拓展：建立通用框架解释各类网络博弈模型之间的关系。
算法与仿真平台：开发高效的模拟平台与可视化工具，促进模型验证与教学传播。
跨学科融合：推动博弈论、人工智能、社会学、网络科学之间的协同研究。

后续学习推荐：

书籍：
- Jackson, M. O. (2008). Social and Economic Networks.
- Easley & Kleinberg. (2010). Networks, Crowds, and Markets.
学术论文：
- Evolutionary Games on Graphs（Science, 2006）
- Game-theoretic Approaches to Influence in Social Networks（IEEE 2011）
实验平台：
- NetLogo、GAMA（模拟平台）
- Python库：NetworkX、Mesa、EvoGame

posted @ 2025-05-19 23:16 郝hai 阅读(1080) 评论(0) 收藏举报

刷新页面返回顶部

指标名称	数学定义或意义
度数（Degree）	节点连接边的数量，\(d_i = \text{deg}(i)\)
平均路径长度	任意两点最短路径的平均值
聚类系数	一个节点的邻居间彼此连接的概率
中心性	如介数中心性、特征向量中心性，衡量节点重要性

联盟 \(S\)	$$v_G(S)$$
\(\{1,2\}\)	10
\(\{2,3\}\)	12
\(\{1,2,3\}\)	18
其他非连通集合	0

haohai9309

格物致知，知行合一！