假设检验决策规则比较:拒绝域、临界值与 p-value
在假设检验中,p-value(p值)是用于衡量样本数据与原假设(null hypothesis)相符程度的概率指标。传统的假设检验方法往往基于拒绝域(Rejection Region)和临界值(Critical Value),而现代统计软件则常以p-value与显著性水平α的比较作为判断标准。以下从三个角度系统比较:拒绝域区间、临界值比较、p-value 的概率区间解释,并给出相关公式和描述。
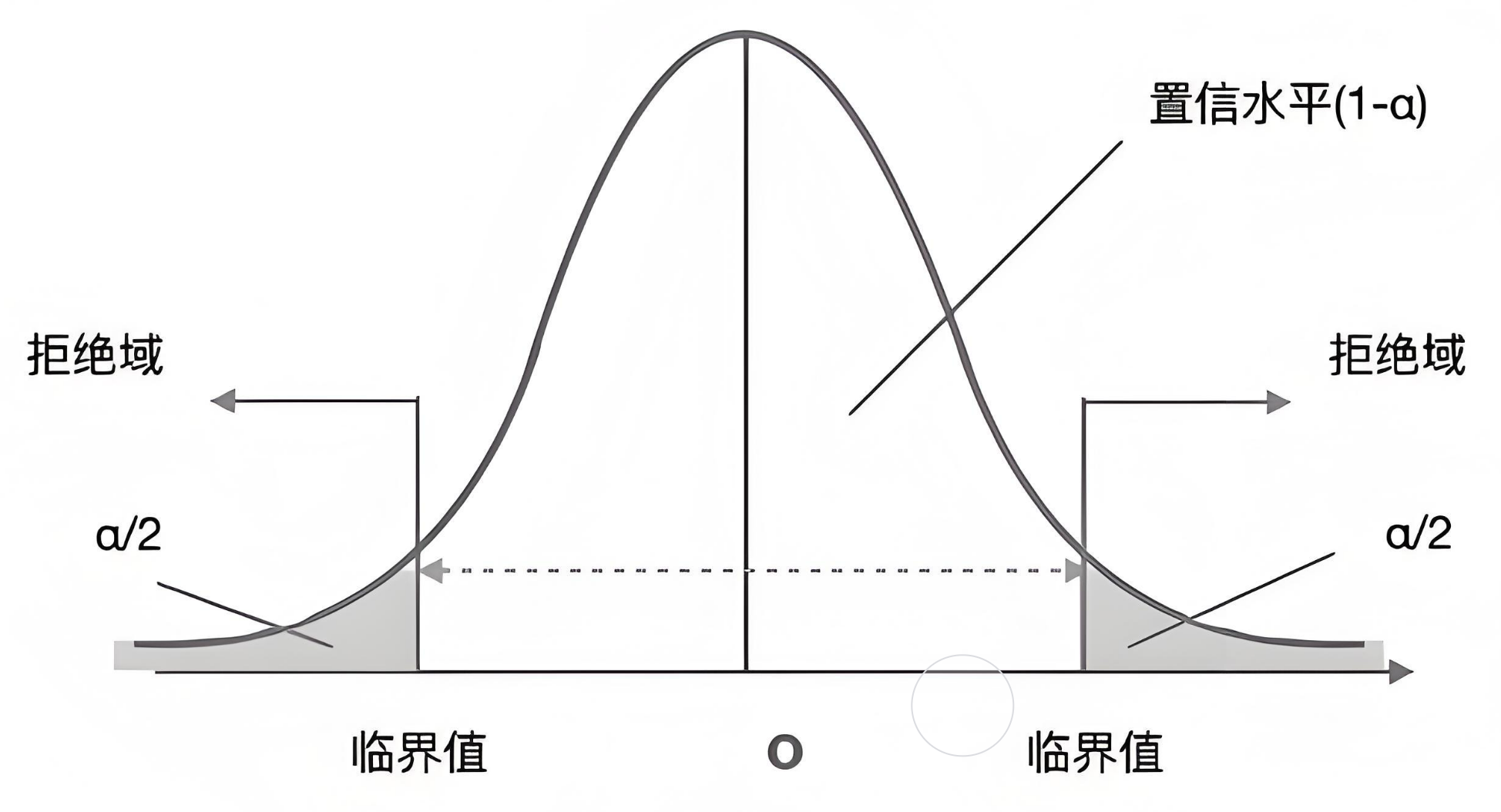
1. 拒绝域区间(Rejection Region)
拒绝域是指在原假设为真时,检验统计量落入该区间的概率很小(不超过显著性水平 \(\alpha\)),因此如果样本统计量落在这个区域中,我们将拒绝原假设。
-
假设设定:
- \(H_0\): \(\mu = \mu_0\)
- 对立假设 \(H_1\): \(\mu \ne \mu_0\)(双侧检验为例)
-
假设检验统计量:
- \(Z = \dfrac{\bar{X} - \mu_0}{\sigma / \sqrt{n}} \sim N(0,1)\) (已知总体方差)
-
拒绝域定义:
- 若 \(|Z| > z_{\alpha/2}\) ⇒ 拒绝 \(H_0\)
- 其中 \(z_{\alpha/2}\) 是标准正态分布的 \(1 - \alpha/2\) 分位点。
图示概念:
拒绝域是在标准正态分布曲线两端的 \(\alpha/2\) 面积部分组成,总面积为 \(\alpha\)。
2. 临界值比较(Critical Value Approach)
临界值法直接与拒绝域方法等价,是在已知显著性水平 \(\alpha\) 的前提下,确定一个与 \(\alpha\) 对应的临界统计值,然后用样本计算得到的检验统计量进行比较。
-
同样的统计量:
- \(Z = \dfrac{\bar{X} - \mu_0}{\sigma / \sqrt{n}}\)
-
显著性水平为 \(\alpha = 0.05\) 的双侧检验,其临界值为:
- \(\pm z_{0.025} = \pm 1.96\)
-
决策规则:
- 若 \(|Z| > 1.96\),拒绝 \(H_0\);
- 若 \(|Z| \le 1.96\),不拒绝 \(H_0\)。
这种方法强调“门槛值”,更适合手动计算和检验表查值使用。
3. p-value 与概率区间解释
p-value 定义:
在原假设 \(H_0\) 成立的前提下,观察到的样本统计量值或更极端的结果出现的概率。
-
公式:
- \(p\text{-value} = P(|Z| > |z_{\text{obs}}|) = 2 \cdot P(Z > |z_{\text{obs}}|)\)
- 其中 \(z_{\text{obs}}\) 是根据样本计算得到的统计量值。
-
决策规则:
- 若 \(p\text{-value} < \alpha\),拒绝 \(H_0\);
- 若 \(p\text{-value} \ge \alpha\),不拒绝 \(H_0\)。
概率区间解释:
p-value 并非某个参数值落入某区间的概率,而是从一个“假设为真”的世界中,计算当前或更极端观测结果的尾部概率。这可以看作一个区间概率:
-
在右尾检验中:
- \(p\text{-value} = P(Z \ge z_{\text{obs}})\)
-
在左尾检验中:
- \(p\text{-value} = P(Z \le z_{\text{obs}})\)
-
在双尾检验中:
- \(p\text{-value} = 2 \cdot P(Z \ge |z_{\text{obs}}|)\)
这相当于在标准正态分布下,对“更极端”的区间求概率。因此:
p-value 小,意味着观测值落入极端区域的概率小,数据对原假设极不支持。
比较总结表
| 比较项 | 拒绝域法 | 临界值法 | p-value 法 |
|---|---|---|---|
| 判定方式 | 检验统计量是否落入拒绝域 | 检验统计量与临界值比较 | p-value 与显著性水平 \(\alpha\) 比较 |
| 拒绝域区间 | $$ |Z| \ge z_{\alpha/2}$$ | $$ |Z| \ge z_{\alpha/2}$$ | $$p-value \le \alpha$$ |
| 是否依赖 \(\alpha\) | 明确依赖 | 明确依赖 | 明确依赖,但可换不同 \(\alpha\) 观察结论变化 |
| 优点 | 可视化强,教学易理解 | 直观,有明确界限 | 精确概率,信息量丰富,灵活适配 \(\alpha\) |
| 缺点 | 不精确,不能反映差异程度 | 只判断,不提供差异大小信息 | 易被误解为“假设成立的概率” |
| 应用场景 | 初学教学,纸质计算 | 教材方法,适合对比不同临界值 | 软件输出,科研论文报告常用 |
举例说明
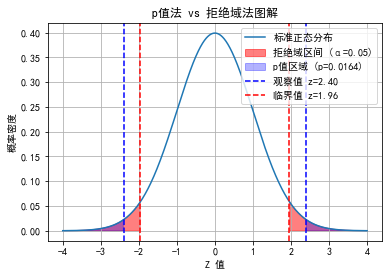
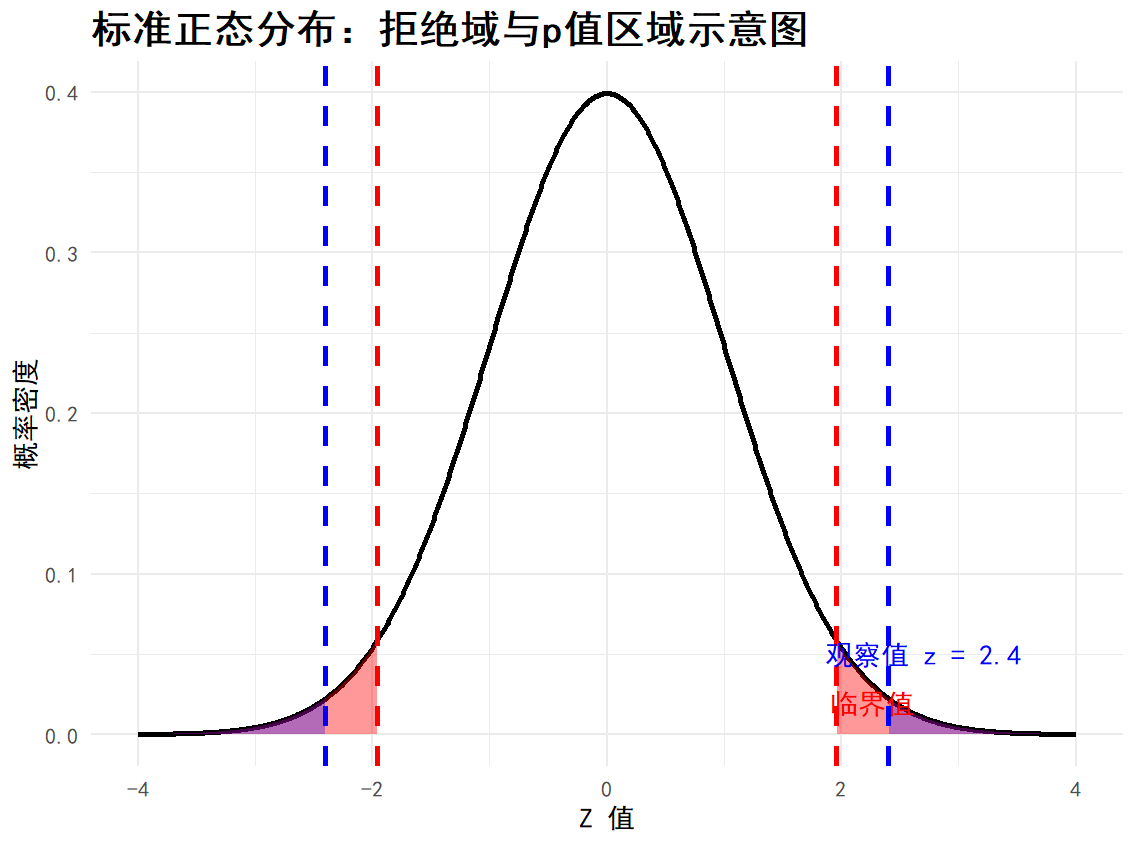
假设某次检验统计量为 \(z_{\text{obs}} = 2.4\),则:
-
\(p = 2 \cdot P(Z > 2.4) = 2 \cdot (1 - \Phi(2.4)) \approx 2 \cdot 0.0082 = 0.0164\)
-
如果 \(\alpha = 0.05\),那么:
- \(p = 0.0164 < 0.05 \Rightarrow\) 拒绝 \(H_0\)
- \(|Z| = 2.4 > 1.96 \Rightarrow\) 拒绝 \(H_0\)
- 落入拒绝域 \(\Rightarrow\) 拒绝 \(H_0\)
三种方法得出一致结论,但 p-value 提供更多概率信息,可用于进一步比较显著性程度。
程序演示
Python
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
# 支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
x = np.linspace(-4, 4, 1000)
y = stats.norm.pdf(x, 0, 1)
z_obs = 2.4
alpha = 0.05
z_critical = stats.norm.ppf(1 - alpha/2)
plt.plot(x, y, label='标准正态分布')
# 拒绝域区域(两尾)
plt.fill_between(x, y, where=(x < -z_critical) | (x > z_critical), color='red', alpha=0.5, label='拒绝域区间 (α=0.05)')
# p值区域
p_val_area = 2 * (1 - stats.norm.cdf(abs(z_obs)))
plt.fill_between(x, y, where=(x > z_obs) | (x < -z_obs), color='blue', alpha=0.3, label='p值区域 (p=%.4f)' % p_val_area)
# 标注线
plt.axvline(z_obs, color='blue', linestyle='--', label='观察值 z=%.2f' % z_obs)
plt.axvline(-z_obs, color='blue', linestyle='--')
plt.axvline(z_critical, color='red', linestyle='--', label='临界值 z=%.2f' % z_critical)
plt.axvline(-z_critical, color='red', linestyle='--')
plt.title('p值法 vs 拒绝域法图解')
plt.xlabel('Z 值')
plt.ylabel('概率密度')
plt.legend()
plt.grid(True)
plt.show()
R程序
# 加载包
library(ggplot2)
# 设置中文字体(根据系统选择一个存在的字体)
windowsFonts(heiti = windowsFont("黑体")) # Windows 系统
# family = "heiti" 可替换为 "STHeiti"(macOS)或 "SimHei"(中文支持字体)
# 参数设置
z_obs <- 2.4
alpha <- 0.05
z_crit <- qnorm(1 - alpha / 2)
# 生成数据
x <- seq(-4, 4, length = 1000)
y <- dnorm(x)
data <- data.frame(x = x, y = y)
# ggplot 绘图
ggplot(data, aes(x = x, y = y)) +
geom_line(color = "black", size = 1) +
# 拒绝域阴影(红色)
geom_area(data = subset(data, x <= -z_crit), aes(y = y), fill = "red", alpha = 0.4) +
geom_area(data = subset(data, x >= z_crit), aes(y = y), fill = "red", alpha = 0.4) +
# p值区域(蓝色)
geom_area(data = subset(data, x >= z_obs), aes(y = y), fill = "blue", alpha = 0.3) +
geom_area(data = subset(data, x <= -z_obs), aes(y = y), fill = "blue", alpha = 0.3) +
# 添加线条
geom_vline(xintercept = c(-z_crit, z_crit), linetype = "dashed", color = "red", size = 1) +
geom_vline(xintercept = c(-z_obs, z_obs), linetype = "dashed", color = "blue", size = 1) +
# 图形设置
ggtitle("标准正态分布:拒绝域与p值区域示意图") +
xlab("Z 值") + ylab("概率密度") +
theme_minimal(base_family = "heiti") +
annotate("text", x = z_crit + 0.3, y = 0.02, label = "临界值", family = "heiti", color = "red") +
annotate("text", x = z_obs + 0.3, y = 0.05, label = "观察值 z = 2.4", family = "heiti", color = "blue") +
theme(
plot.title = element_text(size = 16, face = "bold"),
legend.position = "none"
)
总结
p-value 是一种尾部概率,与显著性水平 α 比较判断假设是否被拒绝。它与拒绝域、临界值方法本质一致,但提供了更精确的概率度量。在实际应用中,软件输出p值成为主流,但理解其与传统方法的一致性和差异,有助于更合理地进行统计推断与解读。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号