塔木德破产分配中的犹太智慧:从博弈出发的公平机制设计
塔木德分配问题源自《塔木德》中关于“两个女人争夺同一件衣服”的经典争产案例,核心在于如何在财产不足以满足所有债权的情况下,公平合理地进行分配。该问题揭示了在资源有限、债权冲突的情形下,兼顾正义与效率的博弈式分配机制。

一、引言:破产中的博弈与分配困境
资源有限而需求无限,是社会中常见的矛盾,而当债务人破产时,债权人面临的分配困境则成为一个典型的博弈问题。每个债权人都希望自己能够获得最大利益,但整体资源有限,这就引发了关于"如何公平分配"的深刻问题。
塔木德破产问题正是从这样的背景中诞生。它最早出现在犹太教经典《塔木德》中,提出一种被称为"塔木德规则"的分配方法,虽然起源于宗教法典,但其中的逻辑和公平思想极具现代价值。现代博弈论特别是合作博弈理论,对这一问题进行了抽象和推广,形成了关于分配规则、公平性和合理性的重要理论分支。
这里将从博弈论的视角出发,系统梳理塔木德破产问题的数学模型与分配规则,依次展开对二人争产、三人争产及N人争产情况的分析,并结合博弈论中的核心概念如“核”、“Shapley值”、“一致性”等予以阐述。通过详细例证与逻辑推导,揭示该分配机制的博弈结构、公平特征及实际应用潜力。
二、博弈论导引:资源分配中的策略互动
博弈论研究多个参与者(博弈人)在策略选择与资源竞争中的互动过程,其核心在于理解利益分配与行为激励。破产分配问题虽看似单纯的财产分配,但本质上隐含了如下博弈结构:
- 资源稀缺性:总资产小于所有债权总额;
- 理性参与者:每个债权人都希望尽可能多获得补偿;
- 可行集合:所有可能的分配方案组成一个凸集;
- 公平性诉求:在既有限制下,寻求合理、公正的分配。
在博弈论中,该类问题属于合作博弈中的分配型博弈(TU game),其目标是对合作联盟如何分享整体收益(或承担整体亏损)进行分析。
三、数学模型定义
设有债权人集合 \(N = \{1, 2, ..., n\}\),每位债权人i的债权为 \(d_i\),总债权额为 \(D = \sum_{i=1}^n d_i\),而债务人仅剩下资产 \(E < D\)。
分配向量 \(x = (x_1, x_2, ..., x_n)\) 满足:
- \(x_i \geq 0\)
- \(x_i \leq d_i\)
- \(\sum_{i=1}^n x_i = E\)
目标是寻找一个满足公平性原则的向量 \(x\)。不同的分配原则给出不同的 \(x\) 值,塔木德规则正是其中一种备受认可的方法。
四、二人争产:塔木德规则的诞生与逻辑
4.1 问题设定
设A债权为 \(d_A = 100\),B债权为 \(d_B = 200\),总财产为 \(E\)。讨论三种情形:
- 情形一:\(E \leq \min(d_A, d_B)\)
- 情形二:\(E \geq \max(d_A, d_B)\)
- 情形三:\(\min(d_A, d_B) < E < \max(d_A, d_B)\)
4.2 塔木德规则(Contested Garment Rule)
该规则的逻辑如下:
- 对于A与B,先将他们的主张(债权)进行平均裁决,即分别获得各自债权的一半;
- 若还有剩余财产,则用于补偿各自未偿部分的争议部分;
- 剩余财产按比例或均等继续分配。
示例1:E = 150,d_A = 100,d_B = 200
- 第一步分配:A得50,B得100;剩余分配总额为150,满足条件,无需调整。
示例2:E = 120
- 初始平均分配:A得50,B得60;已分配110,剩余10
- 剩余10元全部用于B的剩余未偿部分(100),B得10
- 最终:A = 50,B = 70
该规则实质保障了每人债权的下限,并合理调配了剩余部分。
4.3 博弈视角分析
该方案体现了核解特征(每个参与者获得的收益,不少于其在任意联盟中可获得的收益)。同时符合以下条件:
- 个体理性(\(x_i \leq d_i\))
- 群体理性(\(\sum x_i = E\))
- 公平性(不歧视相同角色)
五、三人争产:从线性逻辑到图示机制
5.1 问题设定
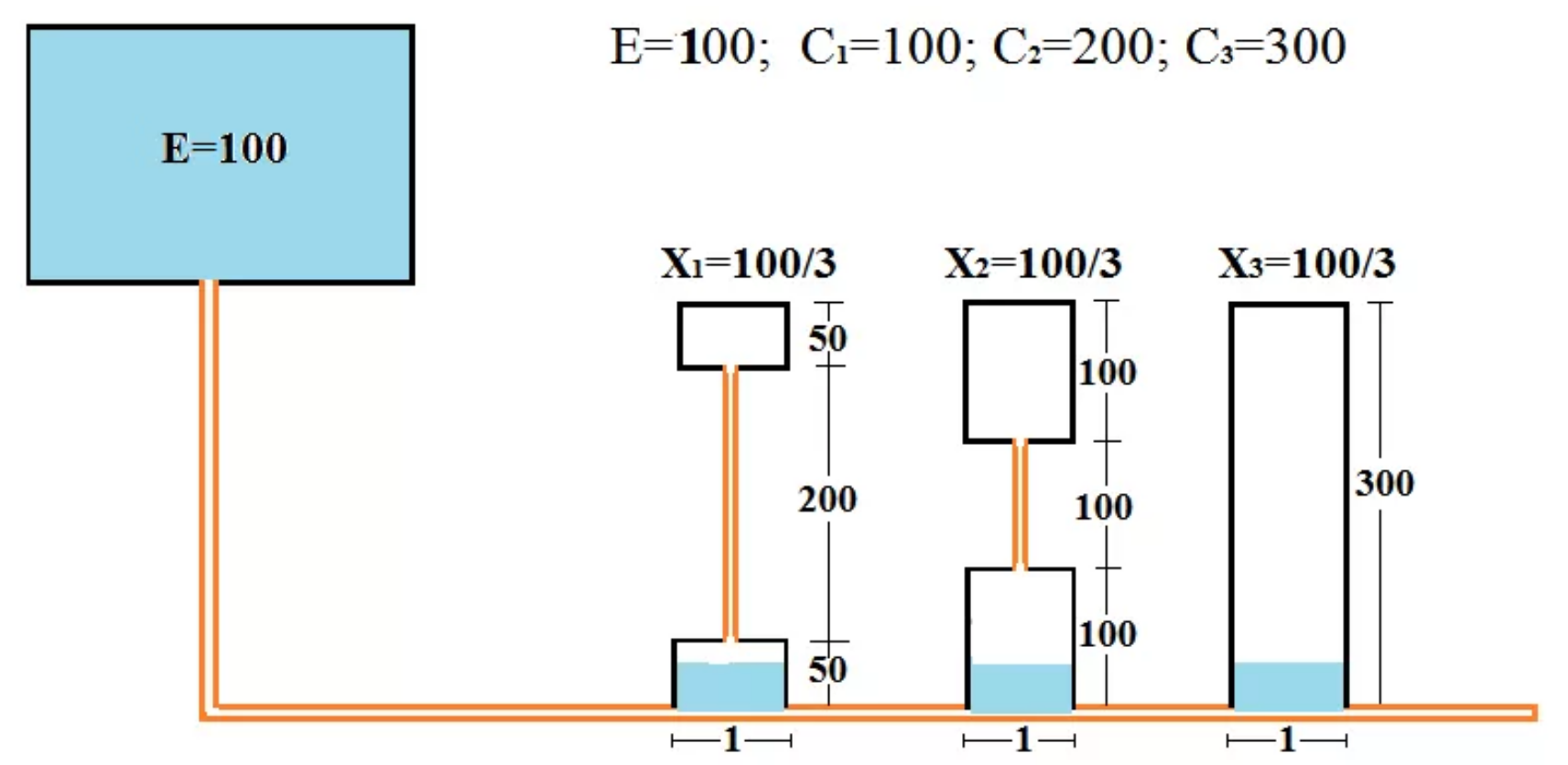
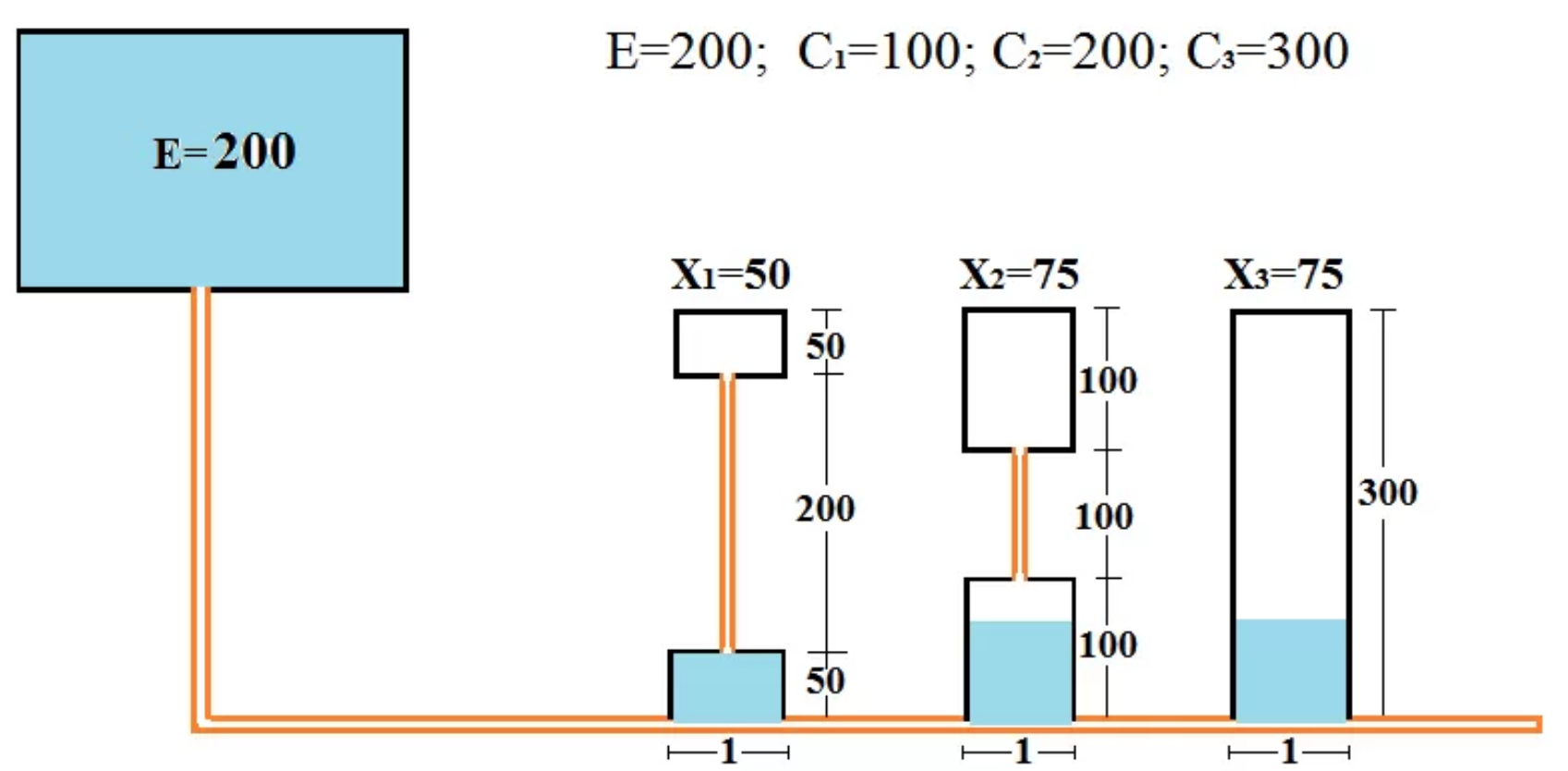
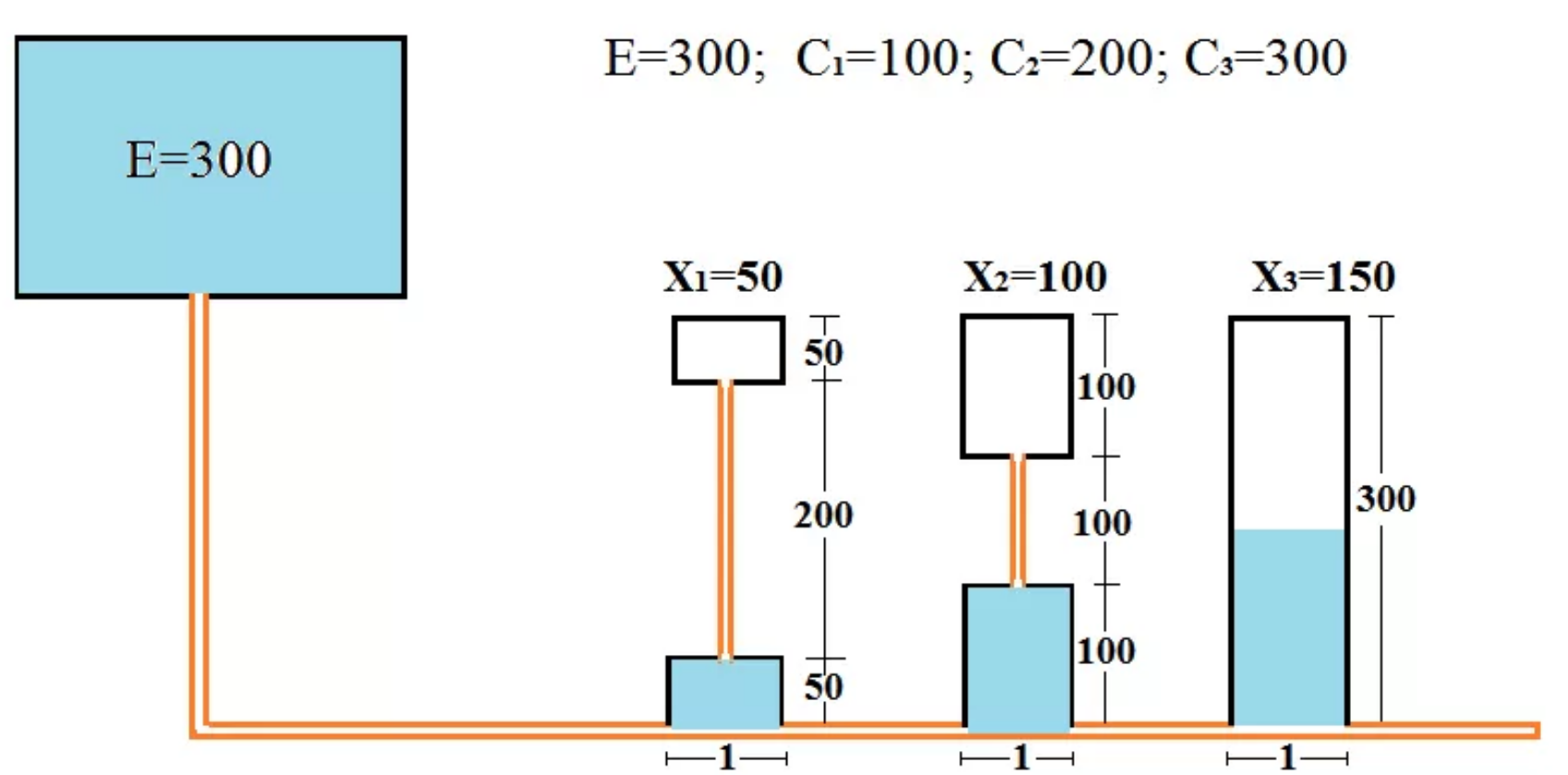
债权人A、B、C的债权分别为100、200、300,总财产E = 300。总债权600 > E。
5.2 分配逻辑
塔木德规则推广如下:
- 每人先拿 \(\min(d_i, \frac{E}{n})\)
- 若还有剩余,按剩余未偿部分再重新分配
- 最终按债权差额调节,保障相对公平
步骤详解:
- 初始分配:每人得100
- 剩余0,停止分配
- 最终:A=100,B=100,C=100(简单情况)
若E = 400:
- 初始:每人得 \(\min(100, 133.33)\) -> A=100,B=133.33,C=133.33;
- A债权已还清,剩余200未偿:B=66.67,C=166.67
5.3 图解法:权利线段图
以坐标表示每人的债权与实际获得的区域,构造“资源线段”,用面积或交点表示剩余部分的分配逻辑,更易可视化理解。
六、N人争产:核解、Shapley值与一致性原则
6.1 核(Core)
核定义:对任意子集 \(S \subseteq N\),分配方案x应满足:
\(\sum_{i \in S} x_i \geq \max(0, E - \sum_{j \notin S} d_j)\)
即使部分联盟脱离,也不能获得比当前方案更好的收益。
塔木德规则构造的分配方案在大多数情况下属于核解集。
6.2 Shapley值
Shapley值提供公平分配的一种依据:
\(\phi_i = \sum_{S \subseteq N \setminus \{i\}} \frac{|S|! (n - |S| - 1)!}{n!} [v(S \cup \{i\}) - v(S)]\)
它度量了个体对整体贡献的边际效应,虽然计算复杂,但理论意义重大。
6.3 一致性(Consistency)
塔木德规则满足一致性:若一个债权人退出或其债权变更,重新分配时其他人的分配比例保持一致。
这在政策制定中至关重要,保障了动态调整下的稳定性与公平性。
七、与其他规则比较
| 分配方法 | 原则基础 | 优点 | 缺点 |
|---|---|---|---|
| 平均分配法 | 每人分得相等 | 简单直观 | 忽视债权差异 |
| 比例分配法 | 按债权比例 | 公平性强 | 小债权人可能受损 |
| 限额平均法 | 限额下平均 | 保障基本权利 | 计算较繁 |
| 塔木德规则 | 下限保障 + 剩余调配 | 兼顾公平与权利 | 推广到N人计算复杂 |
八、实际应用场景与延伸
塔木德破产分配问题不仅是一个经典的博弈论研究案例,更为现实中“资源有限、需求过剩”的冲突提供了合理、公平的解决方案。以下是该规则在多个实际领域中的典型应用与博弈视角分析:
公司破产清算中的债权分配问题
在企业因资不抵债进入破产程序时,面临多个债权人争夺有限资产的局面。传统做法是按债权比例清偿,然而这可能导致小额债权人几乎无法获得保障。塔木德分配规则则提供一种兼顾“最低保障”和“按剩余比例”分配的双重机制,使所有债权人都能至少获得部分债务保障,体现了破产清算中“保护弱者、兼顾公平”的价值取向。从博弈论视角看,该机制减少了对债权清偿排序的争议,提升了债权人间的合作可能性,降低集体诉讼与清算僵局的博弈风险。
医疗资源的危机分配(如疫苗、药品)
在疫情期间,疫苗、抗病毒药物等资源往往短缺,不同地区或人群的需求存在巨大差异。若完全按人口比例分配,容易忽视疫情严重地区的迫切需求;若只按需求分配,又可能忽视资源分配的基本公平性。塔木德规则通过“先分一定保障量,再按剩余需求分配”,可在公平与效率之间寻求平衡。例如,每个城市或人群首先获得基本医疗保障份额,剩余疫苗按感染风险或医护密度再分配,能在道义与效率之间实现协调,缓解公共卫生领域的资源博弈。
水资源跨区域分配
在干旱或水源受限地区,不同行政区对水资源的需求和历史使用权差异显著。若完全依赖历史权利分配,难以满足新兴地区的发展需求;而完全按当前人口需求,又有失对历史使用者的公平。塔木德方案提供一种渐进式调和模型:每个区域先获得“保障性水量”,剩余水资源根据各自尚未满足的水权份额再分配,这种机制促使上下游地区达成可持续的资源共管协议,避免水资源分配中的“零和博弈”。
公地资源共享与制度设计
“公地悲剧”是博弈论中的经典问题,指多个参与者对同一有限资源过度利用最终导致资源枯竭。在此背景下,塔木德破产规则可作为公地管理的一种分配机制。例如,渔业、草场等自然资源可设定最低保障配额给所有用户,剩余资源则依据用户投入、历史权利或生态保护贡献再分配。这不仅降低了资源掠夺动机,也引导形成合作共治的稳定均衡,避免资源耗散。
这些案例表明,塔木德分配规则超越了纯理论模型,具备强大的现实适用性与博弈优化意义,在现代公共资源管理与多方博弈机制设计中具有重要参考价值。
结语:古老智慧与现代博弈的融合
塔木德破产问题以其独特的宗教法律背景和逻辑推理,启发了现代分配机制的理论探索。在博弈论框架下,它不仅成为核、Shapley值等重要概念的实践例子,更是体现了资源约束下公平正义实现的现实思考。当今社会面临的许多挑战,如贫困救助、债务协商、资源保护等,仍可从塔木德破产规则中汲取思维方式与逻辑灵感。在理性博弈与道德哲学之间,我们找到了分配的“黄金分割线”。
塔木德分配问题不仅是一个数学与博弈论中的经典模型,更深刻体现了犹太民族在面对利益冲突时的智慧与价值观。塔木德作为犹太教法律与伦理的核心文献,其对“两个女人争夺一件衣服”的分配讨论,不只是技术上的权衡,更是对公平、仁慈与合作精神的强调。在塔木德分配规则中,每位债权人首先获得一部分基本保障,然后剩余部分再按比例分配,这种“下限保护 + 上限调和”的设计,体现了对弱者的同情与对秩序的追求。犹太智慧强调共赢与责任的伦理导向,认为解决冲突不仅需要逻辑推理,更需道德判断。通过在财产分配中设立“既不能让强者独占,也不能让弱者失衡”的制度安排,塔木德规则实现了理性与道义的平衡。这种思维方式,深植于犹太文化对法律、公平、社会正义的重视,也为后世提供了重要的资源治理与冲突协调的范式。它不仅影响现代博弈论的发展,也启发了现代社会对分配正义的深入思考。
| 1 | 2 | 3 |
|---|---|---|
 |
 |
 |
附注
塔木德破产分配问题(Talmud Bankruptcy Problem)的 Python 程序,适用于任意债权人集合(支持 N 人分配)。程序实现基于 “下限先分 + 上限倒推” 的 Talmud 分配规则,并附有注释说明。
✅ Python 实现:Talmud 分配规则计算器
def talmud_bankruptcy(claims, estate):
"""
计算塔木德破产分配(Talmud Bankruptcy Rule)
参数:
claims: list[float] - 各债权人的债权金额
estate: float - 可用于分配的总财产
返回:
分配结果: list[float]
"""
n = len(claims)
sorted_indices = sorted(range(n), key=lambda i: claims[i]) # 按债权升序排序索引
sorted_claims = [claims[i] for i in sorted_indices]
lower = [min(c / 2, estate / n) for c in sorted_claims] # 下限部分(每人先得一半债权或E/n)
remaining_estate = estate - sum(lower)
# 初始化最终分配 = 下限部分
allocation = lower[:]
# 剩余部分按“债权未偿还部分的一半”逆序分配
upper_claims = [c - l for c, l in zip(sorted_claims, lower)]
while remaining_estate > 1e-8: # 避免浮点误差
total_upper = sum(upper_claims)
if total_upper == 0:
break # 无需再分配
# 每人按未偿部分的比例分配剩余财产
for i in range(n):
share = remaining_estate * upper_claims[i] / total_upper
allocation[i] += share
break # 一轮即可完成
# 将结果还原为原索引顺序
final_allocation = [0] * n
for idx, val in zip(sorted_indices, allocation):
final_allocation[idx] = round(val, 2)
return final_allocation
🧪 示例使用
# 示例:债权人为100, 200, 300,总可分配资产为400
claims = [100, 200, 300]
estate = 400
result = talmud_bankruptcy(claims, estate)
print("塔木德分配结果:", result)
📌 附注说明
- 初步分配(下限):每个债权人先拿自己债权的一半,或平均分配总资产中每人应得的下限部分(取较小值)。
- 剩余分配(上限):剩下的部分用于填补他们的剩余未偿债权(按比例分配)。
- 排序处理:程序中通过排序保证公平性,即优先考虑小额债权人的合理保障。
- 稳定性处理:浮点误差控制在1e-8以下,避免循环分配误差。
- 可扩展性:适用于任意 N 个债权人,只需修改
claims列表与estate值即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号