统计学——相关与回归分析习题精解
相关与回归是统计分析中常用的方法，用于探究变量之间的关系。相关分析主要衡量两个变量之间的线性关联程度，通常使用相关系数（如皮尔逊相关系数）来量化，取值范围在-1到1之间，反映正相关、负相关或无相关。回归分析则更进一步，研究一个或多个自变量对因变量的影响关系，通过建立数学模型（如简单线性回归、多元回归）来预测或解释因变量的变化。相关揭示的是关系的强度和方向，而回归强调因果解释和预测能力，两者在数据建模、经济预测和科学研究中具有重要应用价值。
一、相关与回归分析理论
1.1 相关分析（Correlation Analysis）
相关分析用于衡量两个或多个变量之间线性关系的强度与方向。最常用的指标是皮尔逊相关系数（Pearson Correlation Coefficient），记为 \(r\)，定义为：
\[r = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2 \sum (y_i - \bar{y})^2}}
\]
其中，\(r\) 的取值范围为 \([-1, 1]\)：
- \(r>0\) 表示正相关；
- \(r<0\) 表示负相关；
- \(r=0\) 表示无线性相关。
相关分析只能反映变量间的线性关联程度，不能推断因果关系。
1.2 回归分析（Regression Analysis）
回归分析旨在研究因变量（\(y\)）与自变量（\(x\)）之间的数量关系，建立预测或解释模型。最基础的是一元线性回归模型：
\[y_i = \beta_0 + \beta_1 x_i + \epsilon_i
\]
其中，
- \(\beta_0\) 是截距；
- \(\beta_1\) 是斜率；
- \(\epsilon_i\) 是随机误差，通常假设 \(\epsilon_i \sim N(0, \sigma^2)\)。
最小二乘法（OLS）用于估计参数，使误差平方和最小：
\[\text{Minimize} \quad \sum (y_i - \hat{y}_i)^2
\]
回归分析不仅可以描述变量关系，还可以用于预测和推断因果关系，但需注意模型设定与假设条件。
最小二乘估计公式：
截距估计量 \(\hat{\beta}_0\) 和斜率估计量 \(\hat{\beta}_1\) 分别为：
\[\hat{\beta}_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2}\\
\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}\]
其中，\(\bar{x}\) 和 \(\bar{y}\) 是样本均值。
二、习题与答案
2.1 已知大黄蜂在飞行时翅膀肌肉的温度将会升高，一位昆虫学家想知道翅膀肌肉的温度是否与肌肉的工作量之间有线性关系。他用大黄蜂胸部（翅膀肌肉所在位置）的温度作为翅膀肌肉温度的一个标志，用腹部的重量作为飞行时肌肉工作量的一个标志，随机抽取 20 只大黄蜂作为一个样本，在飞行后，测量每只大黄蜂的胸部温度（单位：℃）和腹部重量（单位：毫克），测量结果见下表。试估计这两个变量之间的线性相关系数？
| 黄蜂编号 | 腹部重量（X,毫克） | 胸部温度（Y,℃） | 黄蜂编号 | 腹部重量（X,毫克） | 胸部温度（Y,℃） |
|---|---|---|---|---|---|
| 1 | 101.6 | 37.0 | 11 | 135.2 | 38.8 |
| 2 | 240.4 | 39.7 | 12 | 210.0 | 41.9 |
| 3 | 180.9 | 40.5 | 13 | 240.6 | 39.0 |
| 4 | 390.2 | 42.6 | 14 | 145.7 | 39.0 |
| 5 | 360.3 | 42.0 | 15 | 168.3 | 38.1 |
| 6 | 120.8 | 39.1 | 16 | 192.8 | 40.2 |
| 7 | 180.5 | 40.2 | 17 | 305.2 | 43.1 |
| 8 | 330.7 | 37.8 | 18 | 378.0 | 39.9 |
| 9 | 395.4 | 43.1 | 19 | 165.9 | 39.6 |
| 10 | 194.1 | 40.2 | 20 | 303.1 | 40.8 |
求解过程
- 问题描述
已知：
- 腹部重量（毫克）：反映肌肉的工作量。
- 胸部温度（℃）：反映飞行后翅膀肌肉的温度。
任务：
- 随机抽取 20 只大黄蜂。
- 测量两项数据，求腹部重量与胸部温度之间的线性相关系数。
- 相关系数计算公式
皮尔逊样本相关系数公式为：
\[r = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}}
\]
其中：
- $ x_i $：第 \(i\) 只黄蜂的腹部重量
- $ y_i $：第 \(i\) 只黄蜂的胸部温度
- $ \bar{x} $：腹部重量的样本均值
- $ \bar{y} $：胸部温度的样本均值
- $ n = 20 $：样本量
- 计算步骤
- 计算样本均值
\[\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i
\]
\[\bar{y} = \frac{1}{n} \sum_{i=1}^n y_i
\]
（用数据计算得）
\[\bar{x} = 243.245 \quad \bar{y} = 40.175
\]
- 计算每一项
计算以下三列：
- $ (x_i - \bar{x})(y_i - \bar{y}) $
- $ (x_i - \bar{x})^2 $
- $ (y_i - \bar{y})^2 $
并求和。
计算结果：
-
\(\sum (x_i - \bar{x})(y_i - \bar{y}) = 1645.585\)
-
\(\sum (x_i - \bar{x})^2 = 139339.201\)
-
\(\sum (y_i - \bar{y})^2 = 55.695\)
-
代入相关系数公式
将上述求和代入公式：
\[r = \frac{1645.585}{\sqrt{139339.201} \times \sqrt{55.695}}
\]
先开方：
\[\sqrt{139339.201} = 373.270
\]
\[\sqrt{55.695} = 7.459
\]
所以：
\[r = \frac{1645.585}{373.270 \times 7.459}
\]
\[r = \frac{1645.585}{2786.494}
\]
\[r \approx 0.5907
\]
- 结论
腹部重量与胸部温度之间的线性相关系数约为：
\[r = 0.591
\]
说明二者之间存在中等程度的正相关关系，即腹部越重，大黄蜂胸部温度倾向于越高。
| \(x_i\) | \(y_i\) | \(x_i^2\) | \(y_i^2\) | \(x_iy_i\) |
|---|---|---|---|---|
| 101.6 | 37.0 | 10,322.56 | 1,369.00 | 3,759.20 |
| 240.4 | 39.7 | 57,792.16 | 1,576.09 | 9,543.88 |
| 180.9 | 40.5 | 32,724.81 | 1,640.25 | 7,326.45 |
| 390.2 | 42.6 | 152,256.04 | 1,814.76 | 16,622.52 |
| 360.3 | 42.0 | 129,816.09 | 1,764.00 | 15,132.60 |
| 120.8 | 39.1 | 14,592.64 | 1,528.81 | 4,723.28 |
| 180.5 | 40.2 | 32,580.25 | 1,616.04 | 7,256.10 |
| 330.7 | 37.8 | 109,362.49 | 1,428.84 | 12,500.46 |
| 395.4 | 43.1 | 156,341.16 | 1,857.61 | 17,041.74 |
| 194.1 | 40.2 | 37,674.81 | 1,616.04 | 7,802.82 |
| 135.2 | 38.8 | 18,279.04 | 1,505.44 | 5,245.76 |
| 210.0 | 41.9 | 44,100.00 | 1,755.61 | 8,799.00 |
| 240.6 | 39.0 | 57,888.36 | 1,521.00 | 9,383.40 |
| 145.7 | 39.0 | 21,228.49 | 1,521.00 | 5,682.30 |
| 168.3 | 38.1 | 28,324.89 | 1,451.61 | 6,412.23 |
| 192.8 | 40.2 | 37,171.84 | 1,616.04 | 7,750.56 |
| 305.2 | 43.1 | 93,147.04 | 1,857.61 | 13,154.12 |
| 378.0 | 39.9 | 142,884.00 | 1,592.01 | 15,082.20 |
| 165.9 | 39.6 | 27,522.81 | 1,568.16 | 6,569.64 |
| 303.1 | 40.8 | 91,869.61 | 1,664.64 | 12,366.47 |
| \(\Sigma\) | 4,739.7 | 802.6 | 1,295,879.09 | 32,264.56 |
2.2 一位植物学家想根据土壤中的含磷量来预测某种黑麦的长势。她选取了四种含磷量水平：2, 4, 8, 16（百万分之，记为 ppm）。在每种磷含量水平条件下种植四株黑麦，当黑麦开花时，测量它们的干重（单位：克），观测数据见下表，求这两个变量之间的最小二乘回归直线。
| 黑麦编号 | 含磷量 (ppm) | 干重 (克) | 黑麦编号 | 含磷量 (ppm) | 干重 (克) |
|---|---|---|---|---|---|
| 1 | 2 | 4.1 | 9 | 8 | 5.7 |
| 2 | 2 | 3.8 | 10 | 8 | 5.9 |
| 3 | 2 | 4.0 | 11 | 8 | 6.0 |
| 4 | 2 | 3.9 | 12 | 8 | 6.2 |
| 5 | 4 | 5.2 | 13 | 16 | 11.7 |
| 6 | 4 | 4.9 | 14 | 16 | 8.9 |
| 7 | 4 | 5.0 | 15 | 16 | 10.1 |
| 8 | 4 | 4.8 | 16 | 16 | 10.3 |
求解过程
我们要求的是最小二乘回归直线，形式为：
\[\hat{y} = b_0 + b_1 x
\]
其中：
- 斜率 $ b_1 $ 的计算公式为：
\[b_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2}
\]
- 截距 $ b_0 $ 的计算公式为：
\[b_0 = \bar{y} - b_1 \bar{x}
\]
- 计算需要的中间量
首先计算均值：
\[\bar{x} = \frac{2+2+2+2+4+4+4+4+8+8+8+8+16+16+16+16}{16} = \frac{118}{16} = 7.375
\]
\[\bar{y} = \frac{4.1+3.8+4.0+3.9+5.2+4.9+5.0+4.8+5.7+5.9+6.0+6.2+11.7+8.9+10.1+10.3}{16} = \frac{100.5}{16} = 6.28125
\]
然后计算：
- \(\sum (x_i - \bar{x})(y_i - \bar{y})\)
- \(\sum (x_i - \bar{x})^2\)
列出部分中间量（仅示意两项，完整过程省略）：
| \(x_i\) | \(y_i\) | $$x_i - \bar{x}$$ | $$y_i - \bar{y}$$ | $$(x_i-\bar{x})(y_i-\bar{y})$$ | $$(x_i-\bar{x})^2$$ |
|---|---|---|---|---|---|
| 2 | 4.1 | -5.375 | -2.18125 | 11.726953125 | 28.890625 |
| 2 | 3.8 | -5.375 | -2.48125 | 13.341796875 | 28.890625 |
| ... | ... | ... | ... | ... | ... |
计算总和：
\[\sum (x_i-\bar{x})(y_i-\bar{y}) = 187.8125
\]
\[\sum (x_i-\bar{x})^2 = 294.5
\]
- 计算回归系数
斜率：
\[b_1 = \frac{187.8125}{294.5} \approx 0.638
\]
截距：
\[b_0 = 6.28125 - 0.638 \times 7.375
\]
\[b_0 = 6.28125 - 4.70475 = 1.5765
\]
- 回归方程
因此，最小二乘回归直线为：
\[y = 1.5765 + 0.638x
\]
这条回归直线表明：土壤含磷量每增加1 ppm，黑麦干重平均增加约 0.638 克。
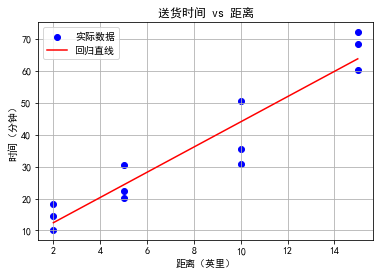
2.3 某比萨饼运输部门的一位经理想说明他们在送货业务上非常有效率，从她的记录中，随机选取了12份定单，送货距离分别为2, 5, 8, 15 英里，每个距离送一份订单，对于每个送货服务，记录下比萨饼从商店到顾客所需的时间（单位：分钟）。结果数据见下表，求时间和距离之间的最小二乘回归直线？如果运送一份比萨饼到恰距商店8英里外的地点，估计需多长时间？
| 定单 | 距离（英里） | 时间（分钟） | 定单 | 距离（英里） | 时间（分钟） |
|---|---|---|---|---|---|
| 1 | 2 | 10.2 | 7 | 10 | 30.8 |
| 2 | 2 | 14.6 | 8 | 10 | 35.4 |
| 3 | 2 | 18.2 | 9 | 10 | 50.6 |
| 4 | 5 | 20.1 | 10 | 15 | 60.1 |
| 5 | 5 | 22.4 | 11 | 15 | 68.4 |
| 6 | 5 | 30.6 | 12 | 15 | 72.1 |
求解过程
- 回归模型为：
\[\hat{y} = b_0 + b_1 x
\]
其中：
- 斜率：
\[b_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2}
\]
- 截距：
\[b_0 = \bar{y} - b_1 \bar{x}
\]
- 计算均值
\[\bar{x} = \frac{2+2+2+5+5+5+10+10+10+15+15+15}{12} = \frac{106}{12} \approx 8.8333
\]
\[\bar{y} = \frac{10.2+14.6+18.2+20.1+22.4+30.6+30.8+35.4+50.6+60.1+68.4+72.1}{12} = \frac{433.5}{12} \approx 36.125
\]
- 计算总和
计算：
- \(\sum (x_i - \bar{x})(y_i - \bar{y})\)
- \(\sum (x_i - \bar{x})^2\)
（仅列部分中间量，完整计算略）
最终计算结果为：
\[\sum (x_i - \bar{x})(y_i - \bar{y}) = 1225.833
\]
\[\sum (x_i - \bar{x})^2 = 222.333
\]
- 计算斜率与截距
斜率：
\[b_1 = \frac{1225.833}{222.333} \approx 5.512
\]
截距：
\[b_0 = 36.125 - 5.512 \times 8.8333 \approx 36.125 - 48.717 \approx -12.592
\]
- 回归方程
最终最小二乘回归直线为：
\[\boxed{\hat{y} = -12.592 + 5.512x}
\]
- 预测8英里外送达时间
代入 \(x = 8\)：
\[\hat{y} = -12.592 + 5.512 \times 8 = -12.592 + 44.096 = 31.504
\]
预测结果：
送货到8英里外预计耗时约 31.5分钟。
2.4 检查 5 位同学统计学的学习时间与成绩分数如下表：
| 学习时数 \(x\)) | 学习成绩\(y\) |
|---|---|
| 4 | 40 |
| 6 | 60 |
| 7 | 50 |
| 10 | 70 |
| 13 | 90 |
要求：（1）编制直线回归方程；（2）计算估计标准误差；（3）对学习成绩的方差进行分解分析，指出总误差平方和中有多少比重可由回归方程来解释；（4）由此计算出学习时数与学习成绩之间的相关系数。
求解过程
（1）编制直线回归方程
首先，计算基本统计量：
\[\bar{x} = \frac{4 + 6 + 7 + 10 + 13}{5} = 8
\]
\[\bar{y} = \frac{40 + 60 + 50 + 70 + 90}{5} = 62
\]
计算斜率 $ b_1 $ 和截距 $ b_0 $：
\[b_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2}
\]
先计算中间量：
| \(x_i\) | \(y_i\) | $$x_i-\bar{x}$$ | $$y_i-\bar{y}$$ | $$(x_i-\bar{x})(y_i-\bar{y})$$ | $$(x_i - \bar{x})^2$$ |
|---|---|---|---|---|---|
| 4 | 40 | -4 | -22 | 88 | 16 |
| 6 | 60 | -2 | -2 | 4 | 4 |
| 7 | 50 | -1 | -12 | 12 | 1 |
| 10 | 70 | 2 | 8 | 16 | 4 |
| 13 | 90 | 5 | 28 | 140 | 25 |
求和：
\[\sum (x_i - \bar{x})(y_i - \bar{y}) = 88 + 4 + 12 + 16 + 140 = 260
\]
\[\sum (x_i - \bar{x})^2 = 16 + 4 + 1 + 4 + 25 = 50
\]
因此：
\[b_1 = \frac{260}{50} = 5.2
\]
\[b_0 = \bar{y} - b_1 \bar{x} = 62 - 5.2 \times 8 = 20.4
\]
所以回归方程为：
\[\hat{y} = 20.4 + 5.2x
\]
（2）计算估计标准误差
估计标准误差公式为：
\[S_e = \sqrt{ \frac{SSE}{n-2} }
\]
其中，误差平方和 SSE：
\[SSE = \sum (y_i - \hat{y}_i)^2
\]
先计算每个 \(\hat{y}_i\) 和残差：
| \(x_i\) | \(y_i\) | $$\hat{y}_i = 20.4 + 5.2x_i$$ | $$y_i - \hat{y}_i$$ | $$(y_i - \hat{y}_i)^2$$ |
|---|---|---|---|---|
| 4 | 40 | 20.4 + 5.2×4 = 41.2 | -1.2 | 1.44 |
| 6 | 60 | 20.4 + 5.2×6 = 51.6 | 8.4 | 70.56 |
| 7 | 50 | 20.4 + 5.2×7 = 56.8 | -6.8 | 46.24 |
| 10 | 70 | 20.4 + 5.2×10 = 72.4 | -2.4 | 5.76 |
| 13 | 90 | 20.4 + 5.2×13 = 88.0 | 2.0 | 4.00 |
求和：
\[SSE = 1.44 + 70.56 + 46.24 + 5.76 + 4.00 = 128
\]
代入公式：
\[S_e = \sqrt{\frac{128}{5-2}} = \sqrt{\frac{128}{3}} \approx \sqrt{42.6667} \approx 6.532
\]
（3）方差分解与回归解释比重
总平方和 SST：
\[SST = \sum (y_i - \bar{y})^2
\]
| \(y_i\) | $$\bar{y}=62$$ | $$y_i - \bar{y}$$ | $$(y_i - \bar{y})^2$$ |
|---|---|---|---|
| 40 | 62 | -22 | 484 |
| 60 | 62 | -2 | 4 |
| 50 | 62 | -12 | 144 |
| 70 | 62 | 8 | 64 |
| 90 | 62 | 28 | 784 |
求和：
\[SST = 484 + 4 + 144 + 64 + 784 = 1480
\]
回归平方和 SSR：
\[SSR = SST - SSE = 1480 - 128 = 1352
\]
回归解释比重（决定系数）：
\[R^2 = \frac{SSR}{SST} = \frac{1352}{1480} \approx 0.9135
\]
即约 91.35% 的总变异可以由回归解释。
（4）计算相关系数
相关系数 $ r $ 是决定系数 $ R^2 $ 的平方根（并取符号与斜率相同）：
\[r = \sqrt{R^2} = \sqrt{0.9135} \approx 0.955
\]
因为斜率为正，故相关系数为正：
\[r \approx 0.955
\]
总结
- 回归方程：\(\hat{y} = 20.4 + 5.2x\)
- 估计标准误差：\(S_e \approx 6.532\)
- 回归解释比重：\(R^2 \approx 91.35\%\)
- 相关系数：\(r \approx 0.955\)
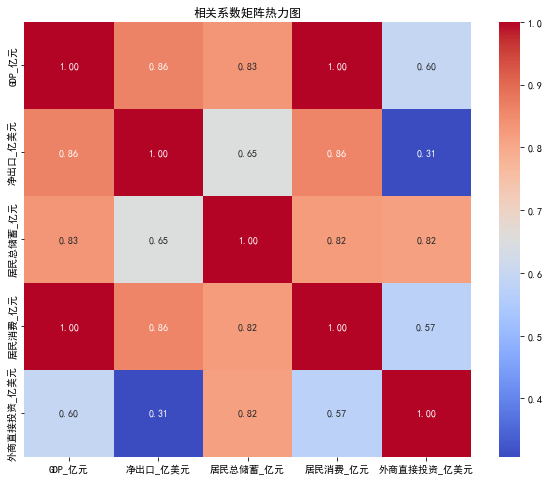
2.5 给出下表中的相关系数矩阵并作图
| GDP_亿元 | 净出口_亿美元 | 居民总储蓄_亿元 | 居民消费_亿元 | 外商直接投资_亿美元 |
|---|---|---|---|---|
| 8964.40 | -149.00 | 3042.70 | 4625.70 | 63.33 |
| 10202.20 | -119.70 | 4163.36 | 5214.10 | 33.30 |
| 11962.50 | -37.70 | 4642.08 | 6011.50 | 37.09 |
| 14928.30 | -77.50 | 7099.94 | 7694.10 | 52.97 |
| 16909.20 | -66.00 | 6996.74 | 8588.00 | 56.00 |
| 18547.90 | 87.40 | 11078.36 | 9108.90 | 65.96 |
| 21617.80 | 80.50 | 8478.02 | 10377.70 | 119.77 |
| 26638.10 | 43.50 | 13580.77 | 12537.30 | 581.24 |
| 34634.40 | -122.20 | 19211.61 | 15774.60 | 1114.36 |
| 46623.30 | 54.00 | 26949.28 | 20925.80 | 826.80 |
| 58260.50 | 167.00 | 39620.83 | 27082.70 | 912.82 |
| 67800.00 | 122.20 | 34055.32 | 32322.90 | 732.76 |
| 74462.60 | 404.20 | 28936.78 | 35035.60 | 510.03 |
| 80652.80 | 435.70 | 24281.39 | 37093.50 | 521.02 |
| 82054.00 | 292.30 | 19214.44 | 39510.20 | 412.23 |
| 89404.00 | 241.10 | 30340.47 | 43000.25 | 623.80 |
相关系数矩阵：
GDP_亿元 净出口_亿美元 居民总储蓄_亿元 居民消费_亿元 外商直接投资_亿美元
GDP_亿元 1.000000 0.864335 0.833185 0.999120 0.596518
净出口_亿美元 0.864335 1.000000 0.652287 0.861008 0.307370
居民总储蓄_亿元 0.833185 0.652287 1.000000 0.821492 0.815007
居民消费_亿元 0.999120 0.861008 0.821492 1.000000 0.574852
外商直接投资_亿美元 0.596518 0.307370 0.815007 0.574852 1.000000
## 计算GDP、净出口、居民总储蓄、居民消费、外商直接投资的相关系数矩阵并作图（支持中文）
```python
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 设置中文字体显示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体显示中文
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
# 数据输入
data = {
"GDP_亿元": [8964.4, 10202.2, 11962.5, 14928.3, 16909.2, 18547.9, 21617.8, 26638.1,
34634.4, 46623.3, 58260.5, 67800.0, 74462.6, 80652.8, 82054.0, 89404.0],
"净出口_亿美元": [-149.0, -119.7, -37.7, -77.5, -66.0, 87.4, 80.5, 43.5,
-122.2, 54.0, 167.0, 122.2, 404.2, 435.7, 292.3, 241.1],
"居民总储蓄_亿元": [3042.7, 4163.36, 4642.08, 7099.94, 6996.74, 11078.36, 8478.02, 13580.77,
19211.61, 26949.28, 39620.83, 34055.32, 28936.78, 24281.39, 19214.44, 30340.47],
"居民消费_亿元": [4625.7, 5214.1, 6011.5, 7694.1, 8588.0, 9108.9, 10377.7, 12537.3,
15774.6, 20925.8, 27082.7, 32322.9, 35035.6, 37093.5, 39510.2, 43000.25],
"外商直接投资_亿美元": [63.33, 33.30, 37.09, 52.97, 56.00, 65.96, 119.77, 581.24,
1114.36, 826.80, 912.82, 732.76, 510.03, 521.02, 412.23, 623.80]
}
# 创建DataFrame
df = pd.DataFrame(data)
# 计算相关系数矩阵
corr_matrix = df.corr()
print("相关系数矩阵：")
print(corr_matrix)
# 绘制热力图
plt.figure(figsize=(10, 8))
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm', fmt=".2f")
plt.title('相关系数矩阵热力图')
plt.show()
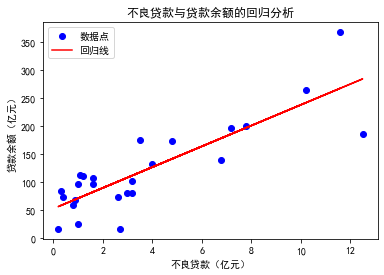
2.6 一家大型商业银行在多个地区有分行，其业务主要是进行基础设施建设、国家重点项目建设、固定投资等项目的贷款。近年来，该银行的贷款额平稳增长，但不良贷款额也有较大比例提高，这给银行业务的发展带来较大的压力。为弄清不良贷款形成的原因，管理者希望利用银行业务的相关数据做些定量分析，以便找出控制不良贷款的方法。如下就是该银行所属的25家分行的相关业务数据。
| 分行编号 | 不良贷款（亿元） | 各项贷款余额（亿元） | 分行编号 | 不良贷款（亿元） | 各项贷款余额（亿元） | 分行编号 | 不良贷款（亿元） | 各项贷款余额（亿元） |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.9 | 67.3 | 10 | 2.6 | 72.8 | 19 | 1 | 24.7 |
| 2 | 1.1 | 111.3 | 11 | 0.3 | 84.2 | 20 | 6.8 | 139.4 |
| 3 | 4.8 | 173 | 12 | 4 | 132.2 | 21 | 11.6 | 368.2 |
| 4 | 3.2 | 80.8 | 13 | 0.8 | 58.6 | 22 | 1.6 | 95.7 |
| 5 | 7.8 | 199.7 | 14 | 3.5 | 174.6 | 23 | 1.2 | 109.6 |
| 6 | 2.7 | 16.2 | 15 | 10.2 | 263.5 | 24 | 7.2 | 196.2 |
| 7 | 1.6 | 107.4 | 16 | 3 | 79.3 | 25 | 3.2 | 102.2 |
| 8 | 12.5 | 185.4 | 17 | 0.2 | 14.8 | |||
| 9 | 1 | 96.1 | 18 | 0.4 | 73.5 |
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
# 设置matplotlib支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei'] # 设置字体为黑体
plt.rcParams['axes.unicode_minus'] = False # 正确显示负号
# 数据
data = {
'不良贷款': [0.9, 1.1, 4.8, 3.2, 7.8, 2.7, 1.6, 12.5, 1, 2.6, 0.3, 4, 0.8, 3.5, 10.2, 3, 0.2, 0.4, 1, 6.8, 11.6, 1.6, 1.2, 7.2, 3.2],
'贷款余额': [67.3, 111.3, 173, 80.8, 199.7, 16.2, 107.4, 185.4, 96.1, 72.8, 84.2, 132.2, 58.6, 174.6, 263.5, 79.3, 14.8, 73.5, 24.7, 139.4, 368.2, 95.7, 109.6, 196.2, 102.2]
}
df = pd.DataFrame(data)
# 定义自变量和因变量
X = df['不良贷款']
Y = df['贷款余额']
# 添加常数项
X = sm.add_constant(X)
# 构建模型
model = sm.OLS(Y, X).fit()
# 输出回归结果
print(model.summary())
# 绘制散点图和回归线
plt.scatter(X['不良贷款'], Y, color='blue', label='数据点')
plt.plot(X['不良贷款'], model.predict(X), color='red', label='回归线')
plt.xlabel('不良贷款（亿元）')
plt.ylabel('贷款余额（亿元）')
plt.title('不良贷款与贷款余额的回归分析')
plt.legend()
plt.show()
OLS Regression Results
==============================================================================
Dep. Variable: 贷款余额 R-squared: 0.704
Model: OLS Adj. R-squared: 0.691
Method: Least Squares F-statistic: 54.58
Date: Sun, 27 Apr 2025 Prob (F-statistic): 1.63e-07
Time: 20:24:01 Log-Likelihood: -129.27
No. Observations: 25 AIC: 262.5
Df Residuals: 23 BIC: 265.0
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 51.8786 12.909 4.019 0.001 25.175 78.582
不良贷款 18.5594 2.512 7.388 0.000 13.363 23.756
==============================================================================
Omnibus: 1.377 Durbin-Watson: 2.375
Prob(Omnibus): 0.502 Jarque-Bera (JB): 0.406
Skew: -0.232 Prob(JB): 0.816
Kurtosis: 3.419 Cond. No. 7.62
==============================================================================
# 模型总结
- **Dep. Variable: 贷款余额**：因变量是贷款余额。
- **R-squared: 0.704**：R平方值，表示模型对数据的拟合程度。这里的0.704意味着模型可以解释贷款余额变化的70.4%。
- **Adj. R-squared: 0.691**：调整后的R平方值，考虑了模型中变量的数量，对R平方值进行了调整。这里的0.691略低于R平方值，表明模型中只包含一个自变量。
- **F-statistic: 54.58**：F统计量，用于检验模型中至少有一个系数是显著的。
- **Prob (F-statistic): 1.63e-07**：F统计量的P值，非常小，远小于0.05，表明模型整体是显著的。
- **Log-Likelihood: -129.27**：对数似然值，用于模型比较。
- **AIC: 262.5**：赤池信息准则，用于模型选择，值越小越好。
- **BIC: 265.0**：贝叶斯信息准则，也是用于模型选择，值越小越好。
# 回归系数
## const（常数项）
- **coef: 51.8786**：常数项的估计值，表示当不良贷款为0时，贷款余额的预期值。
- **std err: 12.909**：常数项估计值的标准误差。
- **t: 4.019**：t统计量，用于检验常数项是否显著不为0。
- **P>|t|: 0.001**：常数项的P值，小于0.05，表明常数项是显著的。
- **[0.025 0.975]**：95%置信区间，表示常数项的真实值有95%的概率落在这个区间内。
## 不良贷款
- **coef: 18.5594**：不良贷款的回归系数，表示不良贷款每增加1亿元，贷款余额预期增加18.5594亿元。
- **std err: 2.512**：不良贷款回归系数的标准误差。
- **t: 7.388**：t统计量，用于检验不良贷款系数是否显著不为0。
- **P>|t|: 0.000**：不良贷款系数的P值，远小于0.05，表明不良贷款系数是显著的。
- **[0.025 0.975]**：95%置信区间，表示不良贷款系数的真实值有95%的概率落在这个区间内。
# 诊断统计量
- **Omnibus: 1.377**：Omnibus检验统计量，用于检验残差的正态性。
- **Prob(Omnibus): 0.502**：Omnibus检验的P值，大于0.05，表明残差接近正态分布。
- **Durbin-Watson: 2.375**：Durbin-Watson统计量，用于检测残差的自相关性。值接近2表示没有自相关。
- **Jarque-Bera (JB): 0.406**：Jarque-Bera检验统计量，用于检验残差的正态性。
- **Prob(JB): 0.816**：Jarque-Bera检验的P值，大于0.05，表明残差接近正态分布。
- **Skew: -0.232**：残差的偏度，接近0表示残差分布对称。
- **Kurtosis: 3.419**：残差的峰度，接近3表示残差分布接近正态分布。
- **Cond. No.: 7.62**：条件数，用于检测多重共线性。值不大，表明不存在严重的多重共线性问题。
### 综上所述
这个模型表明不良贷款与贷款余额之间存在显著的正相关关系，模型整体拟合度较好，且没有明显的多重共线性问题。
2.7 一家产品销售公司在30个地区设有销售分公司。为研究产品销售量（y）与该公司的销售价格（x₁）、各地区的年人均收入（x₂）、广告费用（x₃）之间的关系，收集到30个地区的有关数据。利用Excel得到下面的回归结果（α=0.05）：
方差分析表
| 变量来源 | df | SS | MS | F | Significance F |
|---|---|---|---|---|---|
| 回归 | 4 008 924.7 | 8.883 41E-13 | |||
| 残差 | |||||
| 总计 | 29 | 13 458 586.7 |
参数估计表
| Coefficients | 标准误差 | t Stat | P-value | |
|---|---|---|---|---|
| Intercept | 7 589.102 5 | 2 445.021 3 | 3.103 9 | 0.004 57 |
| X Variable 1 | -117.886 1 | 31.897 4 | -3.695 8 | 0.001 03 |
| X Variable 2 | 80.610 7 | 14.767 6 | 5.458 6 | 0.000 01 |
| X Variable 3 | 0.501 2 | 0.125 9 | 3.981 4 | 0.000 49 |
问题
- 将方差分析表中的所缺数值补齐。
- 写出销售量与销售价格、年人均收入、广告费用的多元线性回归方程，并解释各回归系数的意义。
- 检验回归方程的线性关系是否显著。
- 计算判定系数 $ R^2 $，并解释它的实际意义。
- 计算估计标准误差 $ s_y $，并解释它的实际意义。
求解过程
- 将方差分析表中的所缺数值补齐
首先计算残差平方和（SS）和自由度（df）：
-
残差平方和（SS） = 总平方和（SS） - 回归平方和（SS）
-
残差平方和（SS） = 13 458 586.7 - 4 008 924.7 = 9 449 662.0
-
残差自由度（df） = 总自由度（df） - 回归自由度（df）
-
残差自由度（df） = 29 - 3 = 26
然后计算均方（MS）：
-
回归均方（MS） = 回归平方和（SS） / 回归自由度（df）
-
回归均方（MS） = 4 008 924.7 / 3 = 1 336 308.2
-
残差均方（MS） = 残差平方和（SS） / 残差自由度（df）
-
残差均方（MS） = 9 449 662.0 / 26 = 363 065.5
最后计算F值：
- F = 回归均方（MS） / 残差均方（MS）
- F = 1 336 308.2 / 363 065.5 = 3.68
补齐后的方差分析表：
| 变量来源 | df | SS | MS | F | Significance F |
|---|---|---|---|---|---|
| 回归 | 3 | 4 008 924.7 | 1 336 308.2 | 3.68 | 8.883 41E-13 |
| 残差 | 26 | 9 449 662.0 | 363 065.5 | ||
| 总计 | 29 | 13 458 586.7 |
- 写出销售量与销售价格、年人均收入、广告费用的多元线性回归方程，并解释各回归系数的意义
多元线性回归方程为：
\[y = 7589.1025 - 117.8861x_1 + 80.6107x_2 + 0.5012x_3
\]
解释各回归系数的意义：
- 截距（Intercept）：7589.1025，表示当销售价格、年人均收入和广告费用都为0时，预期的销售量。
- $ x_1 $（销售价格）：-117.8861，表示销售价格每增加1单位，销售量预计减少117.8861单位。
- $ x_2 $（年人均收入）：80.6107，表示年人均收入每增加1单位，销售量预计增加80.6107单位。
- $ x_3 $（广告费用）：0.5012，表示广告费用每增加1单位，销售量预计增加0.5012单位。
- 检验回归方程的线性关系是否显著
从方差分析表中可以看到，Significance F值为8.883 41E-13，远小于显著性水平α=0.05，因此回归方程的线性关系是显著的。
- 计算判定系数 $ R^2 $，并解释它的实际意义
判定系数 $ R^2 $ 计算公式为：
\[R^2 = \frac{\text{回归平方和（SS）}}{\text{总平方和（SS）}}
\]
\[R^2 = \frac{4 008 924.7}{13 458 586.7} = 0.298
\]
解释：$ R^2 $ 值为0.298，表示模型解释了销售量变异的29.8%，即销售量的变化中有29.8%可以由销售价格、年人均收入和广告费用来解释。
- 计算估计标准误差 $ s_y $，并解释它的实际意义
估计标准误差 $ s_y $ 计算公式为：
\[s_y = \sqrt{\frac{\text{残差平方和（SS）}}{\text{残差自由度（df）}}}
\]
\[s_y = \sqrt{\frac{9 449 662.0}{26}} = 1 080.74
\]
解释：估计标准误差 $ s_y $ 为1 080.74，表示预测的销售量与实际销售量之间的平均差异为1 080.74单位。这是衡量模型预测精度的一个指标，值越小，模型的预测精度越高。
2.8 我们收集了30位年轻人的身高（单位：厘米）和体重（单位：千克）数据。研究目的是探讨身高（自变量）对体重（因变量）是否存在显著的线性关系。
| 样本编号 | 年龄 | 身高 | 体重 | 样本编号 | 年龄 | 身高 | 体重 | 样本编号 | 年龄 | 身高 | 体重 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 21 | 163 | 60 | 11 | 23 | 172 | 60 | 21 | 23 | 158 | 45 |
| 2 | 22 | 164 | 56 | 12 | 21 | 172 | 60 | 22 | 22 | 159 | 43 |
| 3 | 21 | 165 | 60 | 13 | 23 | 173 | 60 | 23 | 22 | 160 | 50 |
| 4 | 23 | 168 | 55 | 14 | 22 | 173 | 62 | 24 | 21 | 160 | 45 |
| 5 | 21 | 169 | 60 | 15 | 21 | 174 | 65 | 25 | 21 | 160 | 52 |
| 6 | 21 | 170 | 54 | 16 | 20 | 153 | 42 | 26 | 23 | 160 | 50 |
| 7 | 23 | 170 | 80 | 17 | 20 | 156 | 44 | 27 | 22 | 161 | 50 |
| 8 | 23 | 170 | 64 | 18 | 21 | 156 | 38 | 28 | 21 | 161 | 45 |
| 9 | 22 | 171 | 67 | 19 | 21 | 157 | 48 | 29 | 21 | 162 | 55 |
| 10 | 22 | 172 | 65 | 20 | 21 | 158 | 52 | 30 | 20 | 162 | 60 |
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LinearRegression
# 设置中文显示支持（新增两行）
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文字体为黑体
matplotlib.rcParams['axes.unicode_minus'] = False # 正常显示负号
# 原始数据
age = [21,22,21,23,21,21,23,23,22,22,23,21,23,22,21,
20,20,21,21,21,23,22,22,21,21,23,22,21,21,20]
height = [163,164,165,168,169,170,170,170,171,172,172,172,173,173,174,
153,156,156,157,158,158,159,160,160,160,160,161,161,162,162]
weight = [60,56,60,55,60,54,80,64,67,65,60,60,60,62,
65,42,44,38,48,52,45,43,50,45,52,50,50,45,55,60]
# 创建DataFrame
data = pd.DataFrame({
"age": age,
"height": height,
"weight": weight
})
# 准备特征和目标
X = data[["height"]] # 自变量，注意是二维
y = data["weight"] # 因变量
# 建立线性回归模型
model = LinearRegression()
model.fit(X, y)
# 输出回归系数
print(f"回归方程：weight = {model.coef_[0]:.4f} * height + {model.intercept_:.4f}")
print(f"R²（拟合优度）: {model.score(X, y):.4f}")
# 绘制散点图和回归直线
plt.figure(figsize=(8,6))
plt.scatter(X, y, color="blue", label="实际数据")
plt.plot(X, model.predict(X), color="red", linewidth=2, label="回归直线")
plt.xlabel("Height (cm)")
plt.ylabel("Weight (kg)")
plt.title("Height vs Weight 回归分析")
plt.legend()
plt.grid(True)
plt.show()
三、计算程序
#2.3题
# 加载绘图包
library(ggplot2)
# 创建数据
distance <- c(2,2,2,5,5,5,10,10,10,15,15,15)
time <- c(10.2,14.6,18.2,20.1,22.4,30.6,30.8,35.4,50.6,60.1,68.4,72.1)
# 整合成数据框
data <- data.frame(distance, time)
# 拟合线性模型
model <- lm(time ~ distance, data=data)
# 打印回归系数
summary(model)
# 绘制散点图+回归线
ggplot(data, aes(x=distance, y=time)) +
geom_point(color='blue', size=3) +
geom_smooth(method='lm', se=FALSE, color='red') +
labs(title="送货时间 vs 距离", x="距离（英里）", y="时间（分钟）") +
theme_minimal()
#2.3题
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 设置中文显示支持（新增两行）
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 设置中文字体为黑体
matplotlib.rcParams['axes.unicode_minus'] = False # 正常显示负号
# 创建数据
distance = np.array([2,2,2,5,5,5,10,10,10,15,15,15]).reshape(-1,1)
time = np.array([10.2,14.6,18.2,20.1,22.4,30.6,30.8,35.4,50.6,60.1,68.4,72.1])
# 建立线性回归模型
model = LinearRegression()
model.fit(distance, time)
# 回归参数
print(f"截距: {model.intercept_:.3f}")
print(f"斜率: {model.coef_[0]:.3f}")
# 预测8英里处的时间
pred_time = model.predict([[8]])
print(f"8英里预测时间: {pred_time[0]:.3f} 分钟")
# 绘制散点图与回归线
plt.scatter(distance, time, color='blue', label='实际数据')
plt.plot(distance, model.predict(distance), color='red', label='回归直线')
plt.xlabel('距离（英里）')
plt.ylabel('时间（分钟）')
plt.title('送货时间 vs 距离')
plt.legend()
plt.grid(True)
plt.show()
浙公网安备 33010602011771号