统计学——假设检验习题精解

假设检验基于样本数据对总体参数作出判断，广泛应用于科学实验、质量控制和社会调查等领域，是数据驱动决策的重要依据。

一、假设检验理论

假设检验（Hypothesis Testing）是统计推断中的核心方法，主要用于根据样本数据推断总体参数，并判断某一假设是否成立。基本步骤包括：提出原假设（\(H_0\)）和备择假设（\(H_1\)），选择适当的检验统计量，确定显著性水平（\(\alpha\)），计算P值或拒绝域，并作出推断结论。

一般形式如下：

• 原假设：$ H_0: \theta = \theta_0 $
• 备择假设：\(H_1: \theta \neq \theta_0\)（双侧检验）或 \(\theta > \theta_0\)、\(\theta < \theta_0\)（单侧检验）

常用的检验统计量如：

• 均值检验（总体方差已知）采用标准正态分布：

\[Z = \frac{\bar{X} - \mu_0}{\sigma / \sqrt{n}} \]

• 均值检验（总体方差未知）采用t分布：

\[t = \frac{\bar{X} - \mu_0}{s / \sqrt{n}} \]

其中，$ \bar{X} $ 是样本均值，$ \mu_0 $ 是总体均值假设值，$ \sigma $ 是总体标准差，$ s $ 是样本标准差，$ n $ 是样本容量。

P值是观察到的样本结果在原假设下出现的概率。当P值小于显著性水平\(\alpha\)时，拒绝原假设\(H_0\)。

假设检验常见应用包括：单样本均值检验、双样本均值检验、比例检验、方差检验等。假设检验的本质是在控制第一类错误（拒真错误）概率的前提下，尽可能提高检验的效能（即降低第二类错误）。

方法名称	适用条件	检验目的	常见应用场景	统计量分布	数学公式
Z检验	总体方差已知，或样本量大（n ≥ 30）；数据近似正态	检验总体均值、总体比例	商品合格率、某城市支持率是否超过某值	正态分布	$ Z = \frac{\bar{X} - \mu_0}{\sigma / \sqrt{n}} $
t检验	总体方差未知，样本量小（n < 30）；数据来自正态分布	检验总体均值或两个样本均值差异	药效评估、小规模用户调查、教育实验	t分布	$ t = \frac{\bar{X} - \mu_0}{s / \sqrt{n}} $
双样本Z检验	比较两个总体均值，样本较大或已知方差；两样本独立	检验两个总体均值是否相等	A/B测试、大规模实验组对比	正态分布	$ Z = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}} $
独立样本t检验	两组独立样本，总体方差未知；假设样本方差相等或使用调整公式	检验两组均值是否有显著差异	不同教学方法的考试成绩比较	t分布	\(t = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{S_p^2 \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}}\) 其中 \(S_p^2 = \frac{(n_1 - 1) s_1^2 + (n_2 - 1) s_2^2}{n_1 + n_2 - 2}\)
配对样本t检验	相同个体两次测量（如治疗前后）；关注差值是否为0	比较同一对象在两种条件下的均值差异	医疗干预前后比较、同一人两种测评成绩	t分布	\(t = \frac{\bar{D}}{s_D / \sqrt{n}}\) 其中 \(\bar{D}\) 为差值均值，\(s_D\) 为差值标准差
卡方独立性检验	两个分类变量，构成列联表；样本量足够大（期望频数 ≥ 5）	检验变量之间是否独立	性别与消费偏好是否相关、地区与投票倾向是否独立	卡方分布	\(chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\) 其中\(O_{ij}\)：观察频数，\(E_{ij}\)：期望频数
卡方适合度检验	单个分类变量是否服从某理论分布	检验样本分布是否与理论分布相符	投点试验结果是否符合均匀分布	卡方分布	同上
F检验（方差比检验）	检验两总体方差是否相等；正态分布、独立样本	方差比较、方差齐性检验	比较产品质量波动性、作为ANOVA前提检验	F分布	\(F = \frac{s_1^2}{s_2^2}\)，通常要求 \(s_1^2 > s_2^2\)
方差分析（ANOVA）	三组及以上的独立样本均值比较；正态且方差齐性	检验多组之间均值是否有显著差异	多种教学方法、不同剂量药物疗效对比	F分布	\(F = \frac{\text{组间方差}}{\text{组内方差}} = \frac{MS_{between}}{MS_{within}}\)

二、习题与答案

2.1 某地区小麦的一般生产水平为亩产250千克，其标准差为30千克。现用一种化肥进行试验。从25个地块抽样，平均亩产量为270千克。这种化肥是否使小麦明显增产(α=0.05)?

求解过程

1. 提出假设

• 原假设：$ H_0: \mu = 250 $（没有增产）
• 备择假设：$ H_1: \mu > 250 $（有增产）

2. 已知条件

• 总体标准差已知：$ \sigma = 30 $
• 样本容量：$ n = 25 $
• 样本均值：$ \bar{x} = 270 $
• 显著性水平：$ \alpha = 0.05 $

3. 选择检验统计量

因为总体标准差已知，用Z检验：
\( Z = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}} \)

4. 计算统计量

\( Z = \frac{270 - 250}{30/\sqrt{25}} = \frac{20}{6} \approx 3.333 \)

5. 查Z表临界值

• 单侧检验，\(\alpha = 0.05\)，临界值$ Z_{0.05} = 1.645 $

6. 作出判断

• 由于 $ Z = 3.333 > 1.645 $，拒绝原假设。

结论

在显著性水平0.05下，有充分证据认为这种化肥能使小麦显著增产。

2.2 某种电子元件的寿命x服从正态分布。现测得16只元件的寿命（单位：小时）如下： 159 280 101 212 224 379 179 264 222 362 168 250 149 260 485 170 是否有理由认为元件的平均寿命显著地大于225小时(α=0.05)?

求解过程

1. 提出假设

• 原假设：$ H_0: \mu \ge 225 $
• 备择假设：$ H_1: \mu < 225 $

2. 计算样本均值和样本标准差

设数据为 \(x_1, x_2, \ldots, x_{16}\)。

• 样本均值：

\[\bar{x} = \frac{1}{16} \sum_{i=1}^{16} x_i \]

• 样本标准差：

\[s = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2} \]

经过计算得到：

• \(\bar{x} \approx 243.94\)
• \(s \approx 95.73\)

3. 选择检验统计量

因为总体标准差未知，且样本量较小（\(n = 16\)），使用\(t\)检验：

\[t = \frac{\bar{x} - \mu_0}{s/\sqrt{n}} \]

4. 计算t值

\[t = \frac{243.94 - 225}{95.73/\sqrt{16}} = \frac{18.94}{23.9325} \approx 0.791 \]

5. 查t分布表临界值

• 自由度 \(df = n-1 = 15\)
• 单侧检验，显著性水平 \(\alpha = 0.05\)
• 临界值 \(t_{0.05}(15) \approx 1.753\)

6. 作出判断

• 因为 \(t = 0.791 < 1.753\)，不能拒绝原假设。

结论

在显著性水平0.05下，没有充分证据认为元件的平均寿命显著大于225小时。

2.3 在平炉上进行的一项试验以确定改变操作方法的建议是否会增加刚的得率，试验时在同一个平炉上进行的，每炼一炉刚时除操作方法外，其它条件都尽可能做到相同，先用标准方法炼一炉，然后用新方法炼一炉，以后交替进行，各炼了10炉，其得率分别为

                       标准方法    78.1 72.4 76.2 74.3 77.4 78.4 76.0 75.5 76.7 77.3
                       新方法      79.1 81.0 77.3 79.1 80.0 79.1 79.1 77.3 80.2 82.1

设这两个样本相互独立，且分别来自正态总体N（μ1, σ2)和N（μ2, σ2)，其中μ1，μ2和σ2未知。（1）问新的操作能否提高得率？（取α=0.05）； （2）检验方差是否相同。

求解过程

（1）检验新方法是否提高得率

1. 提出假设

• 原假设 $ H_0: \mu_1 = \mu_2 $（新方法无提高）
• 备择假设 $ H_1: \mu_2 > \mu_1 $（新方法提高了得率）

2. 计算样本统计量

• 标准方法均值 \(\bar{x}_1\)，样本方差 \(s_1^2\)
• 新方法均值 \(\bar{x}_2\)，样本方差 \(s_2^2\)

根据数据计算得到：

• \(\bar{x}_1 = 76.19\)，\(s_1^2 = 3.022\)
• \(\bar{x}_2 = 79.53\)，\(s_2^2 = 2.233\)

3. 选择检验统计量

由于总体方差未知，使用两独立样本t检验。
且假设两个总体方差相等（后面第2问检验方差是否相等）。

使用合并样本方差：

\[s_p^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2} \]

检验统计量为：

\[t = \frac{\bar{x}_2 - \bar{x}_1}{s_p \sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} \]

自由度：

\[df = n_1 + n_2 - 2 = 18 \]

4. 计算具体数值

计算合并样本方差：

\[s_p^2 = \frac{(10-1)\times3.022 + (10-1)\times2.233}{18} = \frac{27.198+20.097}{18} = \frac{47.295}{18} \approx 2.627 \]

\[s_p = \sqrt{2.627} \approx 1.621 \]

计算t值：

\[t = \frac{79.53 - 76.19}{1.621 \times \sqrt{\frac{1}{10}+\frac{1}{10}}} = \frac{3.34}{1.621 \times 0.447} = \frac{3.34}{0.724} \approx 4.615 \]

5. 查t分布临界值

• 单侧检验
• 显著性水平α=0.05，自由度18
• 查表得 $ t_{0.05}(18) = 1.734 $

6. 作出判断

• 因为 $ t = 4.615 > 1.734 $，拒绝原假设。

在显著性水平0.05下，有充分证据认为新的操作方法能显著提高得率。

（2）检验两总体方差是否相等

1. 提出假设

• 原假设 \(H_0: \sigma_1^2 = \sigma_2^2\)
• 备择假设 \(H_1: \sigma_1^2 \neq \sigma_2^2\)

2. 选择检验统计量

采用F检验，统计量：

\[F = \frac{s_1^2}{s_2^2} \]

其中，取较大的方差作为分子。

这里 \(s_1^2 = 3.022\)，\(s_2^2 = 2.233\)，所以

\[F = \frac{3.022}{2.233} \approx 1.353 \]

自由度分别为：

• $ df_1 = 9 $
• $ df_2 = 9 $

3. 查F分布表临界值

• 双侧检验
• 显著性水平α=0.05（两侧各0.025）
• 查表得 \(F_{0.025}(9,9) \approx 4.03\)，\(F_{0.975}(9,9) = 1/4.03 \approx 0.248\)

4. 作出判断

判断标准是：

\[F \in (0.248, 4.03) \]

因为 \(F = 1.353 \in (0.248, 4.03)\)，所以不能拒绝原假设。

在显著性水平0.05下，没有证据表明两总体方差不相等，可以认为方差相等。

2.4 有一批蔬菜种子的平均发芽率p0=0.85，现随即抽取500粒，用种衣剂进行浸种处理，结果有445粒发芽。试检验种衣剂对种子发芽率有无效果。

求解过程

0. 题目数据

• 抽取种子总数 $ n = 500 $
• 发芽粒数 $ x = 445 $
• 样本发芽率 $ \hat{p} = \frac{445}{500} = 0.89 $
• 原发芽率 $ p_0 = 0.85 $
• 显著性水平 $ \alpha = 0.05 $

1. 提出假设

• 原假设 $ H_0: p = 0.85 $ （种衣剂无影响）
• 备择假设 $ H_1: p \neq 0.85 $ （种衣剂有影响）

为双侧检验。

2. 选用检验方法

由于 \(n\) 较大，可以使用正态近似（大样本近似正态分布）。

检验统计量：

\[Z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} \]

3. 计算检验统计量

首先计算标准误差（SE）：

\[SE = \sqrt{\frac{0.85(1-0.85)}{500}} = \sqrt{\frac{0.1275}{500}} \approx 0.01596 \]

计算 $ Z $ 值：

\[Z = \frac{0.89-0.85}{0.01596} \approx \frac{0.04}{0.01596} \approx 2.506 \]

4. 查标准正态分布表

• 双侧检验，显著性水平 $ \alpha=0.05 $
• 查表得临界值 $ Z_{0.025} = 1.96 $

5. 作出决策

• 因为 $ |Z| = 2.506 > 1.96 $，拒绝原假设。
• 在显著性水平0.05下，有充分证据认为种衣剂对种子发芽率有显著影响。

2.5 为研究电话总机在某段时间内接到的呼叫次数是否服从Poisson分布，现收集了42个数据，如下表所示，通过对数据的分析，问能否确认在某段时间内接到的呼叫次数服从Poisson分布（α = 0.1）？

接到呼唤次数	0	1	2	3	4	5	6
出现的频数	7	10	12	8	3	2	0

求解过程

1. 提出假设

• 原假设 $ H_0 $：呼叫次数服从Poisson分布。
• 备择假设 $ H_1 $：呼叫次数不服从Poisson分布。

2. 估计Poisson分布的参数

Poisson分布的参数 $ \lambda $ 取样本均值估计。

计算样本均值：

\[\bar{x} = \frac{\sum (x \times f)}{n} \]

\[\bar{x} = \frac{0\times7 + 1\times10 + 2\times12 + 3\times8 + 4\times3 + 5\times2 + 6\times0}{42} \]

\[\bar{x} = \frac{0+10+24+24+12+10+0}{42} = \frac{80}{42} \approx 1.905 \]

所以估计 $ \lambda = 1.905 $。

3. 计算各类的期望频数

Poisson分布概率公式：

\[P(X=x) = \frac{e^{-\lambda} \lambda^x}{x!} \]

计算各\(x\)的理论概率 \(p_x\)，再乘以样本量$ n=42 $得到期望频数 \(E_x\)。

计算结果：

x	观测频数 \(f_x\)	期望概率 \(p_x\)	期望频数 $$E_x = p_x \times 42$$
0	7	\(e^{-1.905}\frac{1.905^0}{0!} = 0.1487\)	\(6.24\)
1	10	\(e^{-1.905}\frac{1.905^1}{1!} = 0.2833\)	\(11.90\)
2	12	\(e^{-1.905}\frac{1.905^2}{2!} = 0.2698\)	\(11.33\)
3	8	\(e^{-1.905}\frac{1.905^3}{3!} = 0.1711\)	\(7.19\)
4	3	\(e^{-1.905}\frac{1.905^4}{4!} = 0.0815\)	\(3.42\)
5+	2	累积（5,6,...) \(\approx 0.0456\)	\(1.92\)

注意：由于5、6类别频数太小，合并为“5及以上”一组。

4. 计算卡方统计量

卡方统计量公式：

\[\chi^2 = \sum \frac{(f_x - E_x)^2}{E_x} \]

逐项计算：

x	$$(f_x - E_x)^2/E_x$$
0	\((7-6.24)^2/6.24 = 0.092\)
1	\((10-11.90)^2/11.90 = 0.303\)
2	\((12-11.33)^2/11.33 = 0.039\)
3	\((8-7.19)^2/7.19 = 0.089\)
4	\((3-3.42)^2/3.42 = 0.052\)
5+	\((2-1.92)^2/1.92 = 0.003\)

累加得到：

\[\chi^2 = 0.092 + 0.303 + 0.039 + 0.089 + 0.052 + 0.003 = 0.578 \]

5. 自由度

自由度计算公式：

\[df = k - 1 - 1 \]

其中 $ k $ 是分类数（合并后6组），减1是估计了参数$ \lambda $。

所以

\[df = 6 - 1 - 1 = 4 \]

6. 查卡方分布临界值

• 显著性水平 $ \alpha = 0.1 $
• 自由度 $ df = 4 $
• 查表得临界值 $ \chi^2_{0.1}(4) = 7.779 $

7. 作出决策

• 因为 \(\chi^2 = 0.578 < 7.779\)，不能拒绝原假设。
• 在显著性水平0.1下，可以认为呼叫次数服从Poisson分布。

2.6 用两种不同的饲料养猪，其增重情况如下表所示。试分析两种饲料养猪是否有显著差异。

对编号	1	2	3	4	5	6	7	8	9	10	11	12	13	14
饲料 X	25	30	28	23	27	35	30	28	32	29	30	30	31	16
饲料 Y	19	32	21	19	25	31	31	26	30	25	28	31	25	25

求解过程

1. 题目数据

对编号	1	2	3	4	5	6	7	8	9	10	11	12	13	14
饲料 X	25	30	28	23	27	35	30	28	32	29	30	30	31	16
饲料 Y	19	32	21	19	25	31	31	26	30	25	28	31	25	25

2. 提出假设

• 原假设 $ H_0 $：两种饲料对猪的增重无显著差异，即差值均值为0。
• 备择假设 $ H_1 $：两种饲料对猪的增重有显著差异，即差值均值不为0。

3. 计算差值（X - Y）

对编号	饲料X	饲料Y	差值d (X-Y)
1	25	19	6
2	30	32	-2
3	28	21	7
4	23	19	4
5	27	25	2
6	35	31	4
7	30	31	-1
8	28	26	2
9	32	30	2
10	29	25	4
11	30	28	2
12	30	31	-1
13	31	25	6
14	16	25	-9

4. 差值的基本统计量

• 差值样本量：$ n = 14 $
• 差值均值：

\[\bar{d} = \frac{6 + (-2) + 7 + 4 + 2 + 4 + (-1) + 2 + 2 + 4 + 2 + (-1) + 6 + (-9)}{14} \]

先算总和：

\[\text{总和} = 26 \]

所以

\[\bar{d} = \frac{26}{14} \approx 1.857 \]

• 差值样本标准差 $ s_d $：
  先计算平方和：

\[\sum (d_i - \bar{d})^2 \]

这里可以直接算样本方差（用公式法更快）：

\[s_d^2 = \frac{\sum d_i^2 - \frac{(\sum d_i)^2}{n}}{n-1} \]

计算

\[\sum d_i^2 = 6^2 + (-2)^2 + 7^2 + 4^2 + 2^2 + 4^2 + (-1)^2 + 2^2 + 2^2 + 4^2 + 2^2 + (-1)^2 + 6^2 + (-9)^2 \]

即：

\[36 + 4 + 49 + 16 + 4 + 16 + 1 + 4 + 4 + 16 + 4 + 1 + 36 + 81 = 272 \]

代入公式：

\[s_d^2 = \frac{272 - \frac{26^2}{14}}{13} = \frac{272 - 48.2857}{13} = \frac{223.7143}{13} \approx 17.2096 \]

所以

\[s_d \approx \sqrt{17.2096} \approx 4.146 \]

5. 计算t统计量

配对样本t检验公式：

\[t = \frac{\bar{d}}{s_d / \sqrt{n}} \]

代入数值：

\[t = \frac{1.857}{4.146/\sqrt{14}} = \frac{1.857}{1.107} \approx 1.677 \]

6. 自由度

自由度：

\[df = n - 1 = 13 \]

7. 查t分布临界值

在显著性水平 $ \alpha = 0.05 $ ，双尾检验，自由度13查表得：

\[t_{0.05/2}(13) = 2.160 \]

8. 作出决策

• 由于 $ t = 1.677 < 2.160 $，不能拒绝原假设。
• 在显著性水平0.05下，没有足够证据认为两种饲料养猪的增重存在显著差异。

2.7 某电工器材厂生产一种保险丝，测量其熔化时间，假定熔化时间服从正态分布，依通常情况方差为σ² = 400，今从某天产品中抽取容量为25的样本，测量其熔化时间并计算得\(\bar{x} = 62.24\)，\(s^2 = 404.77\)。问这天保险丝熔化时间分散度与通常有无显著差异（α = 0.05）？

1. 题目数据

• 样本容量 $ n = 25 $
• 样本均值 $ \bar{x} = 62.24 $
• 样本方差 $ s^2 = 404.77 $
• 总体方差 $ \sigma^2 = 400 $（通常情况）
• 显著性水平 $ \alpha = 0.05 $

2. 提出假设

• 原假设 $ H_0 $：实际方差与通常无差异，即 $ \sigma^2 = 400 $。
• 备择假设 $ H_1 $：实际方差与通常有差异，即 $ \sigma^2 \neq 400 $（双尾检验）。

3. 检验统计量

检验统计量采用卡方分布：

\[\chi^2 = \frac{(n-1)s^2}{\sigma^2} \]

代入数据计算：

\[\chi^2 = \frac{(25-1) \times 404.77}{400} = \frac{24 \times 404.77}{400} = \frac{9714.48}{400} = 24.2862 \]

4. 自由度

自由度：

\[df = n-1 = 24 \]

5. 查卡方分布临界值

查卡方分布表（自由度24）在显著性水平 $ \alpha = 0.05 $，因为是双尾检验，所以每尾取 $ \alpha/2 = 0.025 $：

• 上临界值 $ \chi^2_{0.975}(24) = 13.848 $
• 下临界值 $ \chi^2_{0.025}(24) = 36.415 $

注意：

• $ \chi^2_{0.025} $是右侧临界值
• $ \chi^2_{0.975} $是左侧临界值

6. 作出决策

判断是否落入拒绝域：

拒绝域是：

\[\chi^2 < 13.848 \quad \text{或} \quad \chi^2 > 36.415 \]

而实际计算得：

\[\chi^2 = 24.2862 \]

显然 $ 13.848 < 24.2862 < 36.415 $，所以没有落入拒绝域。

7. 结论

在显著性水平 $ \alpha = 0.05 $ 下，不能拒绝原假设。
即，这天保险丝的熔化时间分散度与通常情况无显著差异。

2.8 为了研究吸烟是否与患肺癌相关，对63位肺癌患者及43名非肺癌患者（对照组）调查了其中的吸烟人数，得到2x2列联表，如下表所示

	患肺癌	未患肺癌	合计
吸烟	60	32	92
不吸烟	3	11	14
合计	63	43	106

求解过程

0. 题目数据（列联表）

	患肺癌 (A)	未患肺癌 (B)	合计
吸烟	60	32	92
不吸烟	3	11	14
合计	63	43	106

1. 提出假设

• 原假设 $ H_0 $：吸烟与患肺癌无关。
• 备择假设 $ H_1 $：吸烟与患肺癌有关。

2. 检验方法

使用卡方独立性检验。

计算卡方统计量：

\[\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \]

其中：

• $ O_{ij} $：观察频数
• $ E_{ij} $：理论频数，计算公式为：

\[E_{ij} = \frac{(\text{该行合计}) \times (\text{该列合计})}{\text{总体合计}} \]

3. 计算期望频数 $ E_{ij} $

	患肺癌 (A)	未患肺癌 (B)	合计
吸烟	\(\frac{92 \times 63}{106} = 54.717\)	\(\frac{92 \times 43}{106} = 37.283\)	92
不吸烟	\(\frac{14 \times 63}{106} = 8.283\)	\(\frac{14 \times 43}{106} = 5.717\)	14
合计	63	43	106

4. 计算每个单元格的 \(\frac{(O - E)^2}{E}\)

逐项计算：

• 吸烟且患肺癌：

\[\frac{(60 - 54.717)^2}{54.717} = \frac{(5.283)^2}{54.717} \approx 0.510 \]

• 吸烟且未患肺癌：

\[\frac{(32 - 37.283)^2}{37.283} = \frac{(-5.283)^2}{37.283} \approx 0.748 \]

• 不吸烟且患肺癌：

\[\frac{(3 - 8.283)^2}{8.283} = \frac{(-5.283)^2}{8.283} \approx 3.368 \]

• 不吸烟且未患肺癌：

\[\frac{(11 - 5.717)^2}{5.717} = \frac{(5.283)^2}{5.717} \approx 4.883 \]

5. 计算总的卡方统计量

累加得到：

\[\chi^2 = 0.510 + 0.748 + 3.368 + 4.883 = 9.509 \]

6. 自由度

自由度计算公式：

\[df = (r-1)(c-1) \]

其中 \(r=2\)（行数)，\(c=2\)（列数），所以

\[df = (2-1)(2-1) = 1 \]

7. 查卡方分布表

• 显著性水平通常取 $ \alpha = 0.05 $。
• $ df=1 $ 时，查表得：

\[\chi^2_{0.05}(1) = 3.841 \]

8. 作出决策

• 由于 $ \chi^2 = 9.509 > 3.841 $，拒绝原假设。
• 在显著性水平0.05下，有充分证据表明，吸烟与患肺癌有关。

2.9 某医师为研究乙肝免疫球蛋白预防胎儿宫内感染HBV的结果，将33例HBsAg阳性孕妇随即分为预防注射组和对照组，结果由下表所示，问两组新生儿的HBV总体感染率有无差别？

组别	阳性	阴性	合计	感染率 (%)
预防注射组	4	18	22	18.18
对照组	5	6	11	45.45
合计	9	24	33	27.27

求解过程

0. 题目数据（列联表）

组别	阳性	阴性	合计	感染率 (%)
预防注射组	4	18	22	18.18
对照组	5	6	11	45.45
合计	9	24	33	27.27

1. 提出假设

• 原假设 $ H_0 $：两组新生儿HBV感染率无差别。
• 备择假设 $ H_1 $：两组新生儿HBV感染率有差别。

2. 检验方法

由于数据为列联表（2×2表格），可以使用卡方独立性检验。

卡方统计量计算公式为：

\[\chi^2 = \sum \frac{(O_{ij} - E_{ij})^2}{E_{ij}} \]

其中：

• $ O_{ij} $：观察频数
• $ E_{ij} $：理论频数，计算公式为：

\[E_{ij} = \frac{(\text{行合计}) \times (\text{列合计})}{\text{总体合计}} \]

3. 计算期望频数 $ E_{ij} $

	阳性 $ E $	阴性 $ E $	合计
预防注射组	\(\frac{22 \times 9}{33} = 6.0\)	\(\frac{22 \times 24}{33} = 16.0\)	22
对照组	\(\frac{11 \times 9}{33} = 3.0\)	\(\frac{11 \times 24}{33} = 8.0\)	11
合计	9	24	33

4. 计算每个单元格的 $ \frac{(O - E)^2}{E} $

逐项计算：

• 预防注射组阳性：

\[\frac{(4 - 6)^2}{6} = \frac{4}{6} \approx 0.667 \]

• 预防注射组阴性：

\[\frac{(18 - 16)^2}{16} = \frac{4}{16} = 0.25 \]

• 对照组阳性：

\[\frac{(5 - 3)^2}{3} = \frac{4}{3} \approx 1.333 \]

• 对照组阴性：

\[\frac{(6 - 8)^2}{8} = \frac{4}{8} = 0.5 \]

5. 计算总卡方值

累加得到：

\[\chi^2 = 0.667 + 0.25 + 1.333 + 0.5 = 2.75 \]

6. 自由度

自由度计算公式：

\[df = (r-1)(c-1) \]

其中 \(r=2\)，\(c=2\)，所以

\[df = (2-1)(2-1) = 1 \]

7. 查卡方分布表

• 显著性水平通常取 $ \alpha = 0.05 $。
• $ df=1 $ 时，查表得：

\[\chi^2_{0.05}(1) = 3.841 \]

8. 作出决策

• 由于 \(\chi^2 = 2.75 < 3.841\)，不能拒绝原假设。
• 在显著性水平0.05下，没有充分证据表明两组新生儿的HBV感染率有差别。

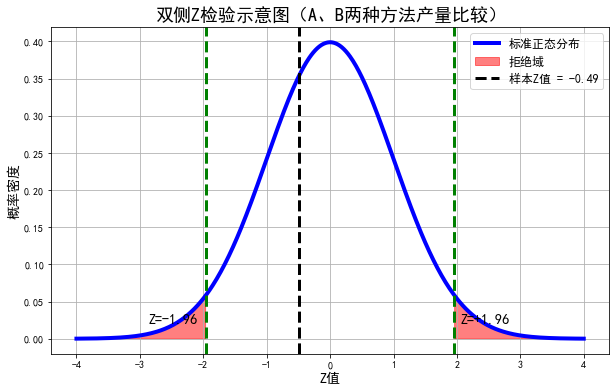
2.10 根据以往资料，已知某品种小麦每4m²产量（单位：kg）的方差为σ² = 0.2。现在在一块地上用A, B两种方法试验。A方法设12个样点，平均产量为1.5公斤；B方法设8个样本点，平均产量为1.6公斤。试比显著性水平0.05下，A, B两法的平均产量是否有显著性的差异？

求解过程

1. 题目数据

• 已知总体方差 $ \sigma^2 = 0.2 $（已知）
• A方法：
  • 样本容量 $ n_1 = 12 $
  • 样本均值 $ \bar{x}_1 = 1.5 $
• B方法：
  • 样本容量 $ n_2 = 8 $
  • 样本均值 $ \bar{x}_2 = 1.6 $
• 显著性水平 $ \alpha = 0.05 $

因为总体方差已知，且假设样本来自正态总体，所以可以用两总体均值之差的Z检验。

2. 提出假设

• 原假设 \(H_0\)：\(\mu_1 = \mu_2\)（即两种方法产量无显著差异）
• 备择假设 \(H_1\)：\(\mu_1 \neq \mu_2\)（即有显著差异）
• 这属于双尾检验。

3. 检验统计量

检验统计量公式为：

\[Z = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\sigma^2 \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}} \]

代入数据计算：

先算标准误差（SE）：

\[SE = \sqrt{0.2 \left( \frac{1}{12} + \frac{1}{8} \right)} = \sqrt{0.2 \times \left( \frac{2+3}{24} \right)} = \sqrt{0.2 \times \frac{5}{24}} = \sqrt{\frac{1}{24}} = 0.2041 \]

然后算Z值：

\[Z = \frac{1.5 - 1.6}{0.2041} = \frac{-0.1}{0.2041} = -0.49 \]

4. 查标准正态分布表

在显著性水平 $ \alpha = 0.05 $ 的双尾检验中，

• 临界值为 $ Z_{0.025} = \pm 1.96 $。

5. 作出决策

因为：

\[-1.96 < Z = -0.49 < 1.96 \]

所以没有落入拒绝域。

6. 结论

在显著性水平 $ \alpha = 0.05 $ 下，不能拒绝原假设。
即：A、B两种方法的平均产量无显著差异。

---

三、计算程序

#2.10题
# 加载中文字体包
library(showtext)
showtext_auto()

# 已知数据
sigma2 <- 0.2
n1 <- 12
n2 <- 8
x1 <- 1.5
x2 <- 1.6

# 计算Z值
sigma <- sqrt(sigma2)
Z <- (x1 - x2) / sqrt(sigma2 * (1/n1 + 1/n2))
cat(sprintf("检验统计量Z = %.3f\n", Z))

# 绘制标准正态分布图
x <- seq(-4, 4, length=500)
y <- dnorm(x)

plot(x, y, type="l", lwd=4, col="blue",
     main="双侧Z检验示意图（A、B两种方法产量比较）", xlab="Z值", ylab="概率密度")

# 拒绝域
alpha <- 0.05
z_alpha <- qnorm(1 - alpha/2)

polygon(c(x[x <= -z_alpha], -z_alpha), 
        c(y[x <= -z_alpha], 0), col=rgb(1,0,0,0.5), border=NA)
polygon(c(x[x >= z_alpha], z_alpha), 
        c(y[x >= z_alpha], 0), col=rgb(1,0,0,0.5), border=NA)

# 样本统计量
abline(v=Z, lty=2, lwd=3, col="black")
abline(v=c(-z_alpha, z_alpha), lty=2, lwd=3, col="green")

text(z_alpha+0.3, 0.02, sprintf("Z=+%.2f", z_alpha), cex=1.2)
text(-z_alpha-0.8, 0.02, sprintf("Z=%.2f", -z_alpha), cex=1.2)

grid()
legend("topright", legend=c("标准正态分布", "拒绝域", "样本Z值"), 
       col=c("blue", "red", "black"), lwd=c(4, 6, 3), lty=c(1,1,2), cex=1)

#2.10题
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 黑体
plt.rcParams['axes.unicode_minus'] = False    # 正确显示负号

# 已知数据
sigma2 = 0.2
n1 = 12
n2 = 8
x1 = 1.5
x2 = 1.6

# 计算Z值
sigma = np.sqrt(sigma2)
Z = (x1 - x2) / np.sqrt(sigma2 * (1/n1 + 1/n2))
print(f"检验统计量Z = {Z:.3f}")

# 绘制标准正态分布图
x = np.linspace(-4, 4, 500)
y = norm.pdf(x)

plt.figure(figsize=(10,6))
plt.plot(x, y, label='标准正态分布', color='blue', linewidth=4)  # 加粗线条

# 填充拒绝域
alpha = 0.05
z_alpha = norm.ppf(1 - alpha/2)
plt.fill_between(x, 0, y, where=(x<=-z_alpha) | (x>=z_alpha), color='red', alpha=0.5, label='拒绝域')

# 标出检验统计量
plt.axvline(Z, color='black', linestyle='--', linewidth=3, label=f'样本Z值 = {Z:.2f}')

# 临界值标注
plt.axvline(z_alpha, color='green', linestyle='--', linewidth=3)
plt.axvline(-z_alpha, color='green', linestyle='--', linewidth=3)
plt.text(z_alpha+0.1, 0.02, f'Z=+{z_alpha:.2f}', fontsize=14)
plt.text(-z_alpha-0.9, 0.02, f'Z=-{z_alpha:.2f}', fontsize=14)

# 图表设置
plt.title('双侧Z检验示意图（A、B两种方法产量比较）', fontsize=18)
plt.xlabel('Z值', fontsize=14)
plt.ylabel('概率密度', fontsize=14)
plt.legend(fontsize=12)
plt.grid()
plt.show()

---