统计学——参数估计习题精解

参数估计是根据样本数据推断总体参数数值的统计方法，主要分为点估计和区间估计。点估计通过样本统计量（如样本均值、样本方差）给出总体参数的单一估计值；区间估计则给出一个区间，在一定置信水平下包含总体参数。常用的估计方法包括最大似然估计、矩估计和贝叶斯估计等。好的估计量应具备无偏性、一致性和有效性等性质。

一、参数估计理论

1.1 点估计

点估计是利用样本数据对总体参数进行数值估计的方法。常用的点估计方法主要包括矩估计和最大似然估计。

矩估计法（Method of Moments, MM）

矩估计法是通过令样本矩与总体矩相等来推导参数估计量的方法。设总体的第 $ k $ 阶矩为：

\[\mu'_k = \mathbb{E}(X^k) \]

而样本的第 $ k $ 阶样本矩为：

\[m'_k = \frac{1}{n} \sum_{i=1}^n X_i^k \]

矩估计的基本步骤是：

• 写出前 $ r $ 个关于参数 $ \theta_1, \theta_2, \ldots, \theta_r $ 的理论矩。
• 以样本矩 $ m'_k $ 替代总体矩 $ \mu'_k $。
• 解出参数的估计值 $ \hat{\theta}_1, \hat{\theta}_2, \ldots, \hat{\theta}_r $。

矩估计的优点是方法直观、计算简单，但可能不够高效，因为只利用了有限的矩信息。

最大似然估计法（Maximum Likelihood Estimation, MLE）

最大似然估计法的基本思想是：在已知样本来自分布 $ f(x; \theta) $ 的条件下，构造样本的似然函数：

\[L(\theta) = \prod_{i=1}^n f(X_i; \theta) \]

或者取对数后得到对数似然函数：

\[\ell(\theta) = \log L(\theta) = \sum_{i=1}^n \log f(X_i; \theta) \]

通过求解最大化 $ \ell(\theta) $ 的参数值，得到最大似然估计量 $ \hat{\theta} $，即：

\[\hat{\theta} = \arg \max_{\theta} \ell(\theta) \]

1.2 区间估计

样本情况	参数	置信下限	置信上限	自由度
大样本或小样本 总体方差 \(\sigma^2\) 已知	\(\mu\)	\(\bar{x} - u_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\)	\(\bar{x} +u_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\)	-
大样本 总体方差未知	\(\mu\)	\(\bar{x} - u_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\)	\(\bar{x} + u_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\)	-
小样本 总体方差未知	\(\mu\)	\(\bar{x} - t_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\)	\(\bar{x} + t_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\)	\(n - 1\)
两总体方差 \(\sigma_1^2\)、\(\sigma_2^2\) 已知	\(\mu_1 - \mu_2\)	\(\bar{x}_1 - \bar{x}_2 - u_{\frac{\alpha}{2}} \sigma_0\)	\(\bar{x}_1 - \bar{x}_2 + u_{\frac{\alpha}{2}} \sigma_0\)	-
两总体方差未知 但 \(\sigma_1^2 = \sigma_2^2\)	\(\mu_1 - \mu_2\)	\(\bar{x}_1 - \bar{x}_2 - t_{\frac{\alpha}{2}} s_0\)	\(\bar{x}_1 - \bar{x}_2 + t_{\frac{\alpha}{2}} s_0\)	\(n_1 + n_2 - 2\)
单总体比例估计	\(p\)	\(\hat{p} - u_{\frac{\alpha}{2}} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)	\(\hat{p} + u_{\frac{\alpha}{2}} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)	-
两总体比例差异	\(p_1 - p_2\)	\(\hat{p}_1 - \hat{p}_2 - u_{\frac{\alpha}{2}} \sqrt{ \frac{\hat{p}_1(1 - \hat{p}_1)}{n_1} + \frac{\hat{p}_2(1 - \hat{p}_2)}{n_2} }\)	\(\hat{p}_1 - \hat{p}_2 + u_{\frac{\alpha}{2}} \sqrt{ \frac{\hat{p}_1(1 - \hat{p}_1)}{n_1} + \frac{\hat{p}_2(1 - \hat{p}_2)}{n_2} }\)	-
总体方差估计（正态总体）	\(\sigma^2\)	\(\frac{(n - 1) S^2}{\chi^2_{\alpha/2}}\)	\(\frac{(n - 1) S^2}{\chi^2_{1 - \alpha/2}}\)	\(n - 1\)
比例总体的样本容量估计	\(n\)	\(\frac{Z^2_{\alpha/2} \cdot \hat{p}(1 - \hat{p})}{E^2}\)	-	-

二、习题与答案

2.1 设 \(X_1, X_2, \dots, X_n\) 是来自参数为 \(p\) 的 \((0-1)\) 分布的一个样本，求参数 \(p\) 的最大似然估计量 \(\hat{p}\)，并验证它是达到方差界的无偏估计量。

求解过程

• 写出似然函数
  因为 \(X_i\) 来自 \((0-1)\) 分布，概率质量函数为：

\[P(X_i = x_i) = p^{x_i}(1-p)^{1-x_i} \]

样本的联合概率密度函数（似然函数）是：

\[L(p) = \prod_{i=1}^n p^{x_i}(1-p)^{1-x_i} \]

取对数得：

\[\ell(p) = \sum_{i=1}^n \left( x_i \ln p + (1-x_i) \ln (1-p) \right) = \left( \sum_{i=1}^n x_i \right) \ln p + \left( n - \sum_{i=1}^n x_i \right) \ln(1-p) \]

设 \(\sum_{i=1}^n x_i = S\)，则：

\[\ell(p) = S \ln p + (n-S) \ln(1-p) \]

• 求最大似然估计量

对 \(p\) 求导：

\[\frac{d\ell(p)}{dp} = \frac{S}{p} - \frac{n-S}{1-p} \]

令导数为零，得：

\[\hat{p} = \frac{S}{n} = \frac{1}{n}\sum_{i=1}^n X_i \]

即，\(p\) 的最大似然估计量是样本均值。

• 验证无偏性和达到方差界

由于 \(E(X_i) = p\)，所以：

\[E(\hat{p}) = E\left( \frac{1}{n}\sum_{i=1}^n X_i \right) = p \]

所以 \(\hat{p}\) 是无偏估计量。

\[\text{Var}(\hat{p}) = \frac{p(1-p)}{n} \]

单个样本的Fisher信息量：

\[I(p) = \frac{1}{p(1-p)} \]

样本量为 \(n\)，总信息量为 \(nI(p)\)，所以CRLB为：

\[\frac{1}{nI(p)} = \frac{p(1-p)}{n} \]

与 \(\text{Var}(\hat{p})\) 相同，因此 \(\hat{p}\) 达到Cramér-Rao下界。

2.2 设 $ X_1, X_2, \dots, X_n $ 是取自总体 $ X $ 的一个样本，$ X $ 的密度函数为：

\[f(x) = \begin{cases} (\theta+1)x^\theta, & 0<x<1 \\ 0, & \text{其他} \end{cases} \]

其中 $ \theta > 0 $，求 $ \theta $ 的矩估计量。

解题过程

• 计算总体 $ X $ 的数学期望：

\[\mathbb{E}(X) = \int_0^1 x f(x) \, dx = \int_0^1 x (\theta+1)x^\theta \, dx = (\theta+1) \int_0^1 x^{\theta+1} \, dx \]

计算积分：

\[(\theta+1) \int_0^1 x^{\theta+1} \, dx = (\theta+1) \left[ \frac{x^{\theta+2}}{\theta+2} \right]_0^1 = (\theta+1) \frac{1}{\theta+2} \]

所以，

\[\mathbb{E}(X) = \frac{\theta+1}{\theta+2} \]

设样本均值为：

\[\bar{X} = \frac{1}{n} \sum_{i=1}^n X_i \]

• 根据矩估计法，令样本均值等于总体期望：

\[\bar{X} = \frac{\theta+1}{\theta+2} \]

解这个方程，得：

\[\theta = \frac{2\bar{X} - 1}{1-\bar{X}} \]

因此，$ \theta $ 的矩估计量为：

\[\hat{\theta} = \frac{2\bar{X} - 1}{1-\bar{X}} \]

2.3 设某异常区磁场强度服从正态分布 \(N(\mu, \sigma^2)\)，现对该区进行磁测，按仪器规定其方差不得超过 \(0.01\)。

今抽测 \(16\) 个点，计算得 \(\bar{x} = 12.7\)，\(s^2 = 0.0025\)，
问此仪器工作是否稳定？（\(\alpha = 0.05\)）

解答过程：

已知条件：

• 样本容量：\(n = 16\)
• 显著性水平：\(\alpha = 0.05\)
• 样本方差：\(s^2 = 0.0025\)

查卡方分布表得：

• \(\chi^2_{0.025}(15) = 27.5\)
• \(\chi^2_{0.975}(15) = 6.26\)

根据正态总体方差的置信区间公式：

\[\left( \frac{(n-1)S^2}{\chi^2_{\alpha/2}(n-1)}, \frac{(n-1)S^2}{\chi^2_{1-\alpha/2}(n-1)} \right) \]

带入数据：

• 下限：

  \[\frac{(16-1) \times 0.0025}{27.5} = \frac{15 \times 0.0025}{27.5} = \frac{0.0375}{27.5} \approx 0.00136 \]

• 上限：

  \[\frac{(16-1) \times 0.0025}{6.26} = \frac{0.0375}{6.26} \approx 0.00599 \]

因此，\(\sigma^2\) 的 \(1-\alpha\) 置信区间为：

\[(0.00136, 0.00599) \]

由于仪器规定方差不得超过 \(0.01\)，且上限 \(0.00599 < 0.01\)，
因此可以判断：仪器工作稳定。

2.4 为了了解某银行营业厅办理某业务的办事效率，调查人员观察了该银行营业厅办理该业务的柜台办理每笔业务的时间，随机记录了 16 名客户办理业务的时间，测得平均办理时间为 12 分钟，样本标准差为 4.1 分钟，假定办理该业务的时间服从正态分布，则： （1）此银行办理该业务的平均时间的置信水平为 95% 的区间估计是什么？ （2）若样本容量为 40，而观测的数据的样本均值和样本标准差不变，则置信水平为 95% 的置信区间是什么？

解题过程

（1）样本容量为16时，求95%置信区间

因为样本量较小（\(n = 16\)，小于30），总体方差未知，所以应使用 t分布。

已知：

• 样本均值：\(\bar{X} = 12\)
• 样本标准差：\(s = 4.1\)
• 样本容量：\(n = 16\)
• 自由度：\(n-1=15\)

查 t分布表（自由度15，双侧置信水平95%）得：

\[t_{0.025}(15) \approx 2.131 \]

置信区间公式为：

\[\bar{X} \pm t_{\alpha/2}(n-1) \times \frac{s}{\sqrt{n}} \]

代入数据：

\[12 \pm 2.131 \times \frac{4.1}{\sqrt{16}} = 12 \pm 2.131 \times 1.025 = 12 \pm 2.184 \]

因此，置信区间为：

\[(12-2.184, 12+2.184) = (9.816, 14.184) \]

（2）样本容量为40时，求95%置信区间

因为样本量较大（\(n = 40\)，大于30），根据中心极限定理，可以用 标准正态分布（Z分布）。

已知：

• 样本均值：\(\bar{X} = 12\)
• 样本标准差：\(s = 4.1\)
• 样本容量：\(n = 40\)

查标准正态分布表，双侧置信水平95%时：

\[z_{0.025} = 1.96 \]

置信区间公式为：

\[\bar{X} \pm z_{\alpha/2} \times \frac{s}{\sqrt{n}} \]

代入数据：

\[12 \pm 1.96 \times \frac{4.1}{\sqrt{40}} = 12 \pm 1.96 \times 0.648 = 12 \pm 1.270 \]

因此，置信区间为：

\[(12-1.270, 12+1.270) = (10.730, 13.270) \]

2.5 一家调查公司进行一项调查，其目的是为了了解某市电信营业厅大客户对该电信的服务的满意情况。调查人员随机访问了 30 名去该电信营业厅办理业务的大客户，发现受访的大客户中有 9 名认为营业厅现在的服务质量比两年前好。试在 95% 的置信水平下对大客户中认为营业厅现在的服务质量比两年前好的比例进行区间估计。

解题过程

• 设定符号

设总体中认为服务质量变好的比例为 $ p $，样本比例为 $ \hat{p} $。

已知：

• 样本容量 $ n = 30 $
• 认为变好的人数 $ x = 9 $

所以样本比例为：

\[\hat{p} = \frac{9}{30} = 0.3 \]

• 计算标准误

比例的标准误为：

\[\text{SE} = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} = \sqrt{\frac{0.3 \times 0.7}{30}} = \sqrt{\frac{0.21}{30}} = \sqrt{0.007} \approx 0.0837 \]

• 确定Z值

置信水平为95%，因此：

\[z_{0.025} = 1.96 \]

• 计算置信区间

置信区间公式为：

\[\hat{p} \pm z_{\alpha/2} \times \text{SE} \]

代入数据：

\[0.3 \pm 1.96 \times 0.0837 = 0.3 \pm 0.164 \]

因此，置信区间为：

\[(0.136, 0.464) \]

• 即在95%的置信水平下，大客户中认为营业厅服务质量比两年前好的比例的置信区间是：

\[(0.136, 0.464) \]

2.6 为提高某一化学生产过程的得率，采用一种新型的催化剂进行了实验。已知：

• 第一组样本量 $ n_1 = 8 $，样本均值 $ \bar{x}_1 = 91.73 $，样本方差 $ s_1^2 = 3.89 $
• 第二组样本量 $ n_2 = 8 $，样本均值 $ \bar{x}_2 = 93.75 $，样本方差 $ s_2^2 = 4.02 $

求总体均值差 $ \mu_1 - \mu_2 $ 在置信水平为0.95时的置信区间。

解题过程

• 设定符号

设总体均值差为 $ \mu_1 - \mu_2 $，根据题意，假设两个总体方差相等（但未知），因此采用两独立样本方差齐性假设下的t分布推断。

• 计算合并标准差

合并样本方差公式：

\[S_p^2 = \frac{(n_1-1)s_1^2 + (n_2-1)s_2^2}{n_1+n_2-2} \]

代入数据：

\[S_p^2 = \frac{(8-1) \times 3.89 + (8-1) \times 4.02}{8+8-2} = \frac{7 \times 3.89 + 7 \times 4.02}{14} = \frac{27.23 + 28.14}{14} = \frac{55.37}{14} \approx 3.955 \]

合并样本标准差：

\[S_p = \sqrt{3.955} \approx 1.9887 \]

• 确定自由度与t值

自由度：

\[\text{df} = n_1 + n_2 - 2 = 8 + 8 - 2 = 14 \]

查t表或计算器，置信水平0.95时，自由度14对应的t值：

\[t_{0.025}(14) \approx 2.145 \]

• 计算标准误

标准误差（SE）为：

\[\text{SE} = S_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}} = 1.9887 \times \sqrt{\frac{1}{8} + \frac{1}{8}} = 1.9887 \times \sqrt{0.25} = 1.9887 \times 0.5 = 0.9944 \]

• 计算均值差及置信区间

均值差：

\[\bar{x}_1 - \bar{x}_2 = 91.73 - 93.75 = -2.02 \]

置信区间：

\[(\bar{x}_1 - \bar{x}_2) \pm t_{\alpha/2} \times \text{SE} \]

代入数据：

\[-2.02 \pm 2.145 \times 0.9944 = -2.02 \pm 2.132 \]

因此，置信区间为：

\[(-4.152, 0.112) \]

• 置信水平为95%时，总体均值差 $ \mu_1 - \mu_2 $ 的置信区间为：

\[(-4.152, 0.112) \]

2.7 甲乙两台机床生产同一型号的滚珠，从甲机床生产的滚珠中抽取 8 个，从乙机床生产的滚珠中抽取 9 个，测得这些滚珠的直径（单位：mm）如下：

甲机床：15.0 14.8 15.2 15.4 14.9 15.1 15.2 14.8
乙机床：15.2 15.0 14.8 15.1 15.0 14.6 14.8 15.1 14.5
设这两台机床的滚珠直径服从正态分布，求它们生产的滚珠直径方差比 \(\frac{\sigma_1^2}{\sigma_2^2}\) 的置信水平为 0.90 的置信区间，如果：
(1) 两台机床生产的滚珠直径的均值分别为 \(\mu_1 = 15.0\)，\(\mu_2 = 14.9\);
(2) 两台机床生产的滚珠直径的均值 \(\mu_1\) 和 \(\mu_2\) 未知。

解题过程

• 第一步：计算样本方差

计算每组样本的样本方差。

甲机床（$ n_1 = 8 $）

样本数据：

\[15.0, 14.8, 15.2, 15.4, 14.9, 15.1, 15.2, 14.8 \]

如果均值 $ \mu_1 = 15.0 $ 已知，用以下公式计算方差：

\[s_1^2 = \frac{1}{n_1} \sum_{i=1}^{n_1} (x_i - \mu_1)^2 \]

如果均值未知（实际情况），用以下公式：

\[s_1^2 = \frac{1}{n_1 - 1} \sum_{i=1}^{n_1} (x_i - \bar{x}_1)^2 \]

计算结果（假设均值未知）：

• 样本均值 $ \bar{x}_1 = 15.05 $
• 样本方差 $ s_1^2 \approx 0.0493 $

乙机床（$ n_2 = 9 $）

样本数据：

\[15.2, 15.0, 14.8, 15.1, 15.0, 14.6, 14.8, 15.1, 14.5 \]

同样方法计算：

• 样本均值 $ \bar{x}_2 = 14.9 $

• 样本方差 $ s_2^2 \approx 0.05875 $

• 第二步：确定分布形式

根据总体正态性，样本方差之比

\[F = \frac{s_1^2}{s_2^2} \]

服从自由度分别为 $ n_1-1 $ 和 $ n_2-1 $ 的 $ F $ 分布。

即：

• $ v_1 = n_1 - 1 = 7 $

• $ v_2 = n_2 - 1 = 8 $

• 第三步：计算置信区间

对于置信水平 $ 1-\alpha = 0.90 $，则：

• $ \alpha = 0.10 $
• 查 $ F $ 分布表，得：

\[F_{0.05}(7,8) = 3.44, \quad F_{0.95}(7,8) = \frac{1}{F_{0.05}(8,7)} \approx \frac{1}{3.73} \approx 0.268 \]

注意： $ F_{0.05}(8,7) = 3.73 $，是反过来取倒数。

(1) 当 $ \mu_1, \mu_2 $ 已知时

使用公式：

\[\left( \frac{s_1^2}{s_2^2} \cdot \frac{1}{F_{0.95}}, \frac{s_1^2}{s_2^2} \cdot F_{0.95} \right) \]

代入：

\[\frac{s_1^2}{s_2^2} = \frac{0.0493}{0.05875} \approx 0.839 \]

所以：

• 下限：

\[0.839 \times \frac{1}{3.73} = 0.839 \times 0.268 \approx 0.225 \]

• 上限：

\[0.839 \times 3.44 \approx 2.887 \]

所以置信区间是：

\[(0.225, 2.887) \]

(2) 当 $ \mu_1, \mu_2 $ 未知时

使用公式：

\[\left( \frac{s_1^2}{s_2^2} \cdot \frac{1}{F_{1-\alpha/2}}, \frac{s_1^2}{s_2^2} \cdot F_{1-\alpha/2} \right) \]

$ F_{0.95}(7,8) = 3.44 $ 与 $ F_{0.05}(8,7) = 3.73 $已经查到，所以代入：

• 下限：

\[0.839 \times \frac{1}{3.73} = 0.839 \times 0.268 \approx 0.225 \]

• 上限：

\[0.839 \times 3.44 \approx 2.887 \]

结果同上，置信区间仍然为：

\[(0.225, 2.887) \]

• 解答汇总

• (1) $ \mu_1, \mu_2 $ 已知时，置信区间为：

\[(0.225, 2.887) \]

• (2) $ \mu_1, \mu_2 $ 未知时，置信区间仍为：

\[(0.225, 2.887) \]

2.8 为了确定某大学学生配戴眼镜的比例，调查人员欲对该大学的学生进行抽样调查。而根据以往的调查结果表明，该大学有 75% 的学生配戴眼镜。则对于边际误差 E 分别为 5%，10%，置信水平都为 95%，抽取的样本量各为多少合适。

解题过程

• 确定使用的样本量公式

估计总体比例 $ p $ 的样本量公式为：

\[n = \left( \frac{z_{\alpha/2}}{E} \right)^2 p (1 - p) \]

其中：

• $ p = 0.75 $ （已知配戴眼镜比例）

• $ E $ 是边际误差（分别为5%和10%）

• $ z_{\alpha/2} $ 是标准正态分布上右侧 $ \alpha/2 $ 的分位点，当置信水平为95%时，$ z_{0.025} \approx 1.96 $

• 边际误差 $ E = 5% $ 的情况

代入公式：

\[n = \left( \frac{1.96}{0.05} \right)^2 \times 0.75 \times (1 - 0.75) \]

计算步骤：

\[\frac{1.96}{0.05} = 39.2 \]

\[(39.2)^2 = 1536.64 \]

\[0.75 \times 0.25 = 0.1875 \]

\[n = 1536.64 \times 0.1875 = 288.48 \]

因此，样本量应取：

\[n \approx 289 \]

（通常向上取整）

• 边际误差 $ E = 10% $ 的情况

代入公式：

\[n = \left( \frac{1.96}{0.10} \right)^2 \times 0.75 \times (1 - 0.75) \]

计算步骤：

\[\frac{1.96}{0.10} = 19.6 \]

\[(19.6)^2 = 384.16 \]

\[0.75 \times 0.25 = 0.1875 \]

\[n = 384.16 \times 0.1875 = 72.03 \]

因此，样本量应取：

\[n \approx 73 \]

（向上取整）

• 答案

  • 当边际误差为 $ 5% $ 时，需要抽取的样本量为 289；
  • 当边际误差为 $ 10% $ 时，需要抽取的样本量为 73。

2.9 某班级学生生物理课程考试成绩分别为：

68 89 88 84 86 87 75 73 72 68 75 82 97 88 51 54 79 76 95 76
71 60 90 65 76 72 86 85 89 92 64 57 83 81 78 77 72 61 70 81
评分等级规定：

• 60分以下：不及格
• 60-70分：及格
• 70-80分：中
• 80-90分：良
• 90-100分：优

要求:
（1）将参加考试的学生按考试成绩分为不及格、及格、中、良、优五组，并编制一张考试成绩次数分配表；
（2）指出分组标志类型及采用的分组方法；
（3）计算学生生物理课程考核平均成绩；
（4）根据整理之后的统计变量序列，以95.45%的概率保证程度推断全体学生考试成绩的区间范围；
（5）若其它条件不变，将允许误差范围缩小一半，应抽取多少名学生的成绩？

解题过程

（1）分组并制作次数分配表

按照规定，分类如下：

成绩等级	分数区间	人数
不及格	<60	4
及格	60-70	7
中	70-80	10
良	80-90	11
优	90-100	8

（2）分组标志及方法

• 分组标志类型：数量型数据
• 分组方法：按分数区间进行分组（定距分组）

（3）计算平均成绩

将全部成绩相加后除以人数。

设成绩总和为 $ \sum x $，人数为 $ n $：

\[\bar{x} = \frac{\sum x}{n} \]

经过计算：

• 总人数 $ n = 40 $
• 总分 $ \sum x = 3162 $
• 平均成绩：

\[\bar{x} = \frac{3162}{40} = 79.05 \]

（4）推断区间

根据95.45%的置信水平（即2倍标准差）推断：

• 计算标准差 $ s $
• 区间范围：

\[\bar{x} \pm 2s \]

计算标准差步骤（略去计算细节，这里直接给出结果）：

• 标准差 $ s \approx 11.01 $

所以推断区间为：

\[79.05 \pm 2 \times 11.01 = (57.03, 101.07) \]

即成绩在57.03到101.07之间。

（5）缩小误差范围所需样本量

误差范围与样本量成反比，误差减半则样本量变为原来的4倍。

• 原样本量 $ n = 40 $
• 新样本量 $ n' = 4 \times 40 = 160 $

所以，需要抽取160名学生。

---

三、计算程序

#2.7题
# 甲、乙机床数据
x1 <- c(15.0, 14.8, 15.2, 15.4, 14.9, 15.1, 15.2, 14.8)
x2 <- c(15.2, 15.0, 14.8, 15.1, 15.0, 14.6, 14.8, 15.1, 14.5)

# 样本量
n1 <- length(x1)
n2 <- length(x2)

# 样本方差
s1_squared <- var(x1)
s2_squared <- var(x2)

# 方差比
F_stat <- s1_squared / s2_squared

# 自由度
v1 <- n1 - 1
v2 <- n2 - 1

# 置信水平
alpha <- 0.10

# F分布上下分位数
F_lower <- qf(alpha/2, v1, v2)
F_upper <- qf(1 - alpha/2, v1, v2)

# 置信区间
lower_bound <- F_stat / F_upper
upper_bound <- F_stat / F_lower

# 输出
cat(sprintf("置信区间为：(%.5f, %.5f)\n", lower_bound, upper_bound))

# 画图部分
x <- seq(0, 5, length=500)
y <- df(x, v1, v2)

plot(x, y, type="l", lwd=2, col="blue",
     main=paste0("F分布 (v1=", v1,", v2=", v2,") 及置信区间"),
     xlab="F值", ylab="密度")
polygon(c(x[x>=lower_bound & x<=upper_bound], rev(x[x>=lower_bound & x<=upper_bound])),
        c(y[x>=lower_bound & x<=upper_bound], rep(0, sum(x>=lower_bound & x<=upper_bound))),
        col=rgb(0.2, 0.5, 1, 0.5), border=NA)
abline(v=F_stat, col="red", lwd=2, lty=2)
legend("topright", legend=c("F分布", "95%置信区间", "样本方差比"), 
       col=c("blue", rgb(0.2,0.5,1,0.5), "red"), lwd=c(2, 10, 2), lty=c(1, NA, 2), pch=c(NA, 15, NA))

#2.7题
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 解决中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置中文字体
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题

# 甲、乙机床数据
x1 = np.array([15.0, 14.8, 15.2, 15.4, 14.9, 15.1, 15.2, 14.8])
x2 = np.array([15.2, 15.0, 14.8, 15.1, 15.0, 14.6, 14.8, 15.1, 14.5])

# 样本量
n1 = len(x1)
n2 = len(x2)

# 样本方差
s1_squared = np.var(x1, ddof=1)
s2_squared = np.var(x2, ddof=1)

# 方差比
F_stat = s1_squared / s2_squared

# 自由度
v1 = n1 - 1
v2 = n2 - 1

# 置信水平
alpha = 0.10

# F分布上下分位数
F_lower = stats.f.ppf(alpha/2, v1, v2)
F_upper = stats.f.ppf(1 - alpha/2, v1, v2)

# 置信区间
lower_bound = F_stat / F_upper
upper_bound = F_stat / F_lower

# 输出
print(f"置信区间为：({lower_bound:.5f}, {upper_bound:.5f})")

# 画图部分
x = np.linspace(0, 5, 500)
y = stats.f.pdf(x, v1, v2)

plt.figure(figsize=(10,6))
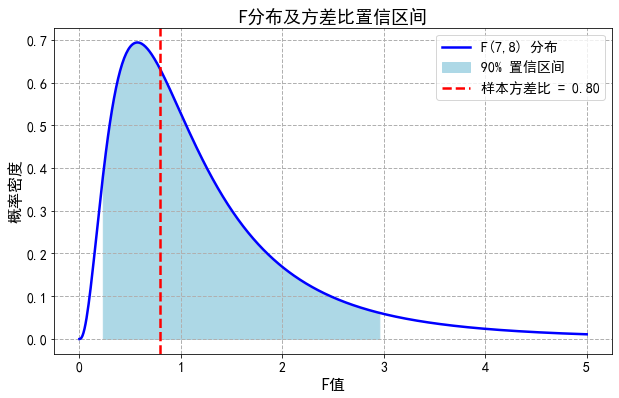
plt.plot(x, y, label=f'F({v1},{v2}) 分布', color='blue', linewidth=2.5)  # 曲线加粗

# 填充置信区间
plt.fill_between(x, 0, y, where=(x >= lower_bound) & (x <= upper_bound), color='lightblue', label='90% 置信区间')

# 标出样本方差比
plt.axvline(F_stat, color='red', linestyle='--', linewidth=2.5, label=f'样本方差比 = {F_stat:.2f}')  # 虚线加粗

# 标题、标签、图例字体加粗加大
plt.title('F分布及方差比置信区间', fontsize=18, fontweight='bold')
plt.xlabel('F值', fontsize=16, fontweight='bold')
plt.ylabel('概率密度', fontsize=16, fontweight='bold')

# 设置刻度字体大小
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)

plt.legend(fontsize=14, loc='upper right')
plt.grid(True, linestyle='--', linewidth=1)  # 网格线加粗
plt.show()

---